Multiple CO₂ capture in stable metal-doped graphene: a theoretical trend study

Abstract

Identifying stable systems with high CO₂ adsorption capacity is an essential goal in CO₂ capture and storage technologies. We have carried out a comprehensive first-principles study to explore the CO₂ capture capacity of 16 representative metal-doped graphene systems where the metal dopants can be stabilized by single- and double-vacancies. The maximum number of adsorbed CO₂ molecules was determined by a combination of adsorption energy and bond distance criteria. Generally, while the double-vacancy can bind metal dopants more strongly than the single-vacancy, single-vacancy graphene with metal dopants are better sorbents, with each Ca, Sc and Y dopant binding up to 5 CO₂ molecules. CO₂ capture involves significant charge transfer between the CO₂ molecule and the dopant–vacancy complexes, where defective graphene acts as a charge reservoir for binding CO₂ molecules. Some systems are predicted to involve the formation of a bent CO₂ anion. Ca-doped single- and double-vacancy graphene systems, however, readily form oxides upon reaction with CO₂, thus they are less reusable for CO₂ capture.

---

1 Introduction

Carbon dioxide capture and storage (CCS) is a group of technologies dedicated to the capture of CO₂ followed by compression, transport, and storage. It is an intense area of research because it represents a key approach for curbing CO₂ emission and reducing the impact of energy production on climate change.^1–3 CCS implemented in modern power plants is estimated to reduce CO₂ emission by 80–90%.² However, currently the capture alone will increase the energy requirements of a plant by 25–40% because existing methods of capture are energy intensive and are not cost effective.^2,4–6 Therefore, intensive research efforts are directed towards achieving effective and energy-efficient capture technologies.

New alternative materials are being investigated, such as porous coal, activated carbons (AC),³ metal–organic frameworks (MOFs),⁷ zeolites and fullerenes.⁸ Recently, low-dimensional carbon-based materials including graphene, graphene oxide⁹ and carbon nanotubes (CNTs)¹⁰ have been considered as promising adsorbents for CO₂.⁸ As such, they have been widely investigated by various research groups at low and very high CO₂ pressures.³ This is because of their large surface area, easy-to-design pore structures, surface functionalization and low energy requirements for regeneration. In particular, a graphene sheet with adsorbed gases could be regenerated to its initial state within 100–200 s by annealing at 150 °C in vacuum or short ultra-violet irradiation.¹¹ Furthermore, it was experimentally¹² demonstrated that using graphene for CO₂ capture, at a pressure of 11 bar and room temperature, has a higher capture capacity than other carbon nanostructures and zeolites. Recently, the reactivity of graphene was also shown to be tunable by varying the external electric field.¹³

Functionalization and doping are known to alter the chemical properties of graphene sheets to enhance their response to gases. Studies show that nitrogen doping of graphene enhances its CO₂ capture capacity.^14,15 Nanostructured polyaniline decorated graphene was investigated by Mishra et al.⁸ and found to have high selectivity, and nitrogen doping was shown to enhance CO₂ capture in a microporous carbon system.^16,17 Doping with metal adatoms is expected to be even more appealing due to the inherent diversity of their chemical properties. Metal adatoms adsorbed on pristine, single vacancy (SV) and double vacancy (DV) graphene sheets¹⁸ have been studied, on the basis of first principles density functional theory (DFT) calculations, owing to the feasibility of performing fine deposition of adatoms into the graphene surface.¹⁹ Fabrication of DV rich graphene has been achieved experimentally through high energy ion bombardment.²⁰ Deposition of Pt on graphene was the subject of a recent experimental investigation,²¹ and Al was theoretically^22,23 and experimentally²⁴ shown to improve the adsorption ability and sensitivity of carbon nanotubes and graphene towards gases. In the present study, we focus on the so-called 585-type DV configuration which is less stable than the reconstructed 555777 configuration by about 0.9 eV.²⁴ However, to our knowledge, the 555777-type DV has not yet been experimentally fabricated, while the 585 configuration has been produced by high energy ion bombardment.²⁰ It is possible that combining metal species with DV and SV graphene will enhance their sensitivity and selectivity by favouring adsorption/desorption processes. Theoretical studies show that DV and SV graphene can stablise metal adatoms and overcome the clustering difficulty, thus facilitating device applications.^18,25

It is easy to envisage that different metal dopants may have different binding behavior with CO₂.²⁶ In this regard, the maximum CO₂ adsorption capacity is a key parameter in identifying potential CCS materials. However, to our knowledge, existing ab initio studies in the literature consider only one CO₂ molecule capture. Moreover, a systematic trend study is appealing in evaluating different candidate systems for CO₂ capture, yet such an investigation is still lacking. Here, we perform a comprehensive DFT trend study of the adsorption capacities of metal adatoms on SV and DV graphene. We consider multiple CO₂ capture on 16 different metal–graphene systems (metal M = Al, Ca, Co, Cr, Cu, Fe, Mg, Mn, Nb, Ni, Pt, Sc, Ti, V, Y, and Zr). These metallic elements were selected to test the performance of species known to exhibit high sensitivity to gases as well as to explore the capacity of elements that have seldom been explored for CO₂ capture to date. In particular, we consider elements of the first row of transition metal (TM) elements which have good sensing properties to CO₂ in their bulk oxide form.²⁷ We denote the metal–graphene system with the notation M/DV (metal atom adsorbed on double-vacancy graphene) and M/SV (metal atom adsorbed on single-vacancy graphene).

We focus primarily on the atomic structure, energetics, charge transfer and charge distribution in these systems to determine their CO₂ capture and storage capacity. A few elements among the 16 investigated (namely, Ca, Nb, Sc, Zr and Y) were found to have exceptionally high CO₂ adsorption capability. Our study reveals that CO₂ capture involves significant charge transfer between the CO₂ molecule and the dopant–vacancy complexes, where defective graphene acts as a charge reservoir for binding CO₂ molecules. Interestingly, the CO₂ anion forms in the Ca and Nb systems where the first adsorbed CO₂ molecule experiences significant bending, and acquires a negative charge.

2 Calculation details

We perform spin-unrestricted density functional theory (DFT) calculations with the SIESTA code,²⁸ using the generalized gradient approximation (GGA) for the exchange–correlation functional as developed by Perdew, Burke and Ernzerhof (PBE).²⁹ SIESTA uses basis sets comprised of numerical atomic orbitals, and approximates the atomic potential in terms of Troullier–Martins³⁰ norm-conserving pseudopotentials. The auxiliary basis set uses a real-space mesh with a kinetic energy cutoff of 500 Ry, and the basis functions are radially confined using an energy shift of 0.005 Ry (see ref. 28 for details). Our simulation consists of a rectangular 72-atom graphene sheet with lattice parameters a = 12.896 Å and b = 14.942 Å. The calculated lattice constant of graphene is 2.48 Å, which is in very good agreement with the experimental value of 2.46 Å (ref. 31) and previous DFT GGA calculations (e.g. 2.44 Å and 2.47 Å from ref. 31 and 32, respectively). A reciprocal-space k-point mesh of 5 × 5 × 1 is used. We allow full atomic relaxation until the forces on the atoms are less than 0.03 eV Å⁻¹.

3 Results and discussion

The adsorption energies of the metal adatom on the defective graphene surface, and the average adsorption energies of CO₂ molecules on metal-doped DV/SV graphene are given below:

E^M_ad = E_M/SV(DV)Gr − E_SV(DV)Gr − E^M_free (1)

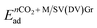where E^M_ad is the adsorption energy of the metal atom on SV/DV graphene, E_M/SV(DV)Gr is the total energy of the M/DV(SV) system, E_SV(DV)Gr is the total energy of the SV(DV) graphene sheet unit cell, E^M_free is the energy of the free metal atom, is the average adsorption energy of nCO₂ molecules on the M/SV(DV) system, is the total energy of the M/SV(DV) system with n adsorbed CO₂ molecules and is the total energy of the free CO₂ molecule (note, we do not include the vacancy formation energy, as typically the defective graphene systems are produced by ion-bombardment).

3.1 Metal atom adsorption on SV and DG graphene

We first investigate the atomic and electronic structure, and energetics of the metal–graphene systems for adsorption on SVs and DVs. The vertical distances of the metal adatoms to the graphene plane, the adsorption energies (eqn (1)) and associated total unit-cell magnetic moments are presented in Fig. 1. The results are in reasonable agreement with values reported in an earlier theoretical work.²⁵ Generally, adsorption on DV graphene results in shorter vertical distances because one DV has a larger hole with four edge carbon atoms, while one SV has three edge carbon atoms. Ca atoms adsorb with the highest vertical distance (2.40 Å in Ca/SV, 1.98 Å in Ca/DV) and with the lowest adsorption energy (−1.35 eV in Ca/SV, −0.74 eV in Ca/DV). The 3d TMs bind at vertical distances in the range 1.3 Å to 1.7 Å (except for Sc which is 1.93 Å), while 4d TMs adsorb at relatively larger vertical distances because of the larger ionic radius. The systems Mg/SV and Mg/DV also have relatively low adsorption energy (−1.52 eV in Mg/SV, −1.72 eV for Mg/DV). All of the TMs considered bind relatively strongly with the C atoms with adsorption energies ranging from −7.98 eV for Zr/SV to −3.51 eV for Cu/SV. Comparing with the adatom adsorption energies reported in ref. 33, several metal species are predicted to bind more strongly to DV or SV graphene than to covalent organic frameworks, namely Ti, Sc, Ca and Mg.

Fig. 1 For each element, the white box shows the maximum adsorption capacities of SV and DV systems. The blue box shows the vertical distance (relative to the plane of graphene, in Å) of the M adatom and the red box shows the total magnetic spin moment (in μ_B). The bottom grey row of the box shows the adsorption energy of the metal adatom on SV/DV graphene. The vertical distance and total magnetic moment are for the doped systems before adsorbing the first CO₂ (at left side of the arrow, the “pure” system) and after adsorption of the maximum number of CO₂ molecules (at the right side of the arrow, the “full” system).

The magnetization of the adatom/graphene systems is shown in units of μ_B on the red background in Fig. 1. The undoped DV/graphene is non-magnetic, and the undoped SV/graphene has a spin moment of 1.62 μ_B (in agreement with ref. 34). The Ti, Sc, Ni Al, Y, Zr, and Pt adatoms totally quench the spin polarization of the SV/graphene system, while Mn, Ca and Mg increases the spin polarization of the SV/graphene structure the most (2.95 μ_B, 1.95 μ_B and 1.95 μ_B, respectively). For the DV/graphene system, doping with Ti, Mg, Zr, Ni and Cu does not magnetize the system, whereas doping with the rest of the considered elements does. Maximum magnetization in doped DV/graphene systems occur in Mn/DV and Fe/DV (3.42 μ_B and 3.76 μ_B, respectively).

We study charge transfer by using the Voronoi deformation density method³⁵ as is implemented in SIESTA. In the metal-doped SV and DV graphene structures considered, the metal atoms always donate charge to the graphene sheet, mainly to the edge C atoms of the vacancies. For each species, the amount of donated charge is similar in SV and DV systems. The largest charge transfer occurs in Pt/SV and Pt/DV systems, where the Pt atom loses 0.78e in both systems. The Ni atom for the Ni/DV system loses the least amount of charge (0.073e), while in the Ni/SV, Co/SV, Fe/SV, the adatom loses electron charge from 0.1e to 0.3e. For the rest of the systems the adatom loses electron charge ranging from 0.3e to 0.6e.

3.2 CO₂ adsorption on adatom/SV and DV graphene

To ascribe the number of CO₂ molecules that a system can bind, we adopt a combination of two criteria: (1) the average adsorption energy (eqn (2)) should be above 0.3 eV, and (2) the distance between the additional adsorbed CO₂ molecule and the metal adatom be less than 4 Å (the distance for this purpose is defined as the distance between the metal adatom and the closest atom of the CO₂ molecule). We have chosen the 0.3 eV threshold arbitrarily based on the physisorption threshold in the literature,³⁶ and the value of 4 Å based on the correlation between the average adsorption energies as they approach 0.3 eV and the associated bond distances. We add the n^th CO₂ molecules to the relaxed structure with (n − 1) CO₂ molecules as long as both criteria are satisfied. In this manner, the adsorption capacities are assigned as given in Fig. 1. In order to confirm that our atomic relaxation calculations have yielded structural minima, we have performed relaxation with different initial configurations for the case of adsorption of two CO₂ molecules at Ca/SV, Mg/SV, and Sc/SV. For each species, we obtained identical total energies and consistent converged structures giving confidence in our approach.

Among the systems considered, the distance between the metal adatom and the bonded CO₂, the shortest distance is for Co/SV (2.02 Å), Fe/SV (2.00 Å) and Ni/SV (2.05 Å). For the systems with highest capture capacities (Ca, Nb, Y, Sc, Y and Zr), the distances are within the range 2.2–2.7 Å. An interesting aspect of CO₂ adsorption on M/SV and M/DV systems is the angle of inclination of the CO₂ molecule to the graphene surface. For some systems with collinear CO₂, the CO₂ molecule aligns almost parallel to the plane of the graphene sheet. These systems are Fe/DV, Cu/DV, Mn/DV, Ni/DV, Pt/DV, Ti/DV, V/DV and Y/DV. Interestingly, Mg/DV, Mg/SV and Pt/SV are predicted to align the CO₂ molecule vertically (Fig. 2).

Fig. 2 Atomic structure of the systems with highest adsorption capacities. C, O and metal atoms are represented by small grey (yellow), small dark (red) and large grey spheres, respectively.

Based on the calculated average adsorption energy, the following systems bond very weakly to the first adsorbed CO₂ molecule, and hence, do not have good potential as CO₂ sorbent systems: Al/DV (−0.20 eV), Ti/DV (−0.08 eV), Cu/DV (−0.12 eV), Pt/DV (−0.09 eV), V/DV (−0.08 eV), Mn/DV (−0.08 eV), Fe/DV (−0.07 eV), Y/DV (−0.09 eV), Co/DV (−0.02 eV), Ni/DV (−0.13 eV), V/SV (−0.04 eV), Pt/SV (−0.23 eV) and Cu/SV (−0.26 eV). Thus, for these systems, we set the CO₂ capacity to be zero (Fig. 1). Fig. 3 shows the average adsorption energy as a function of the number of CO₂ molecules adsorbed in systems which can bind more than one CO₂ molecule. Results are shown for adsorption on both the SV (Fig. 3(a)) and DV (Fig. 3(b)) structures. The maximum number of adsorbed CO₂ molecules are as follows: Ca/DV (5), Ca/SV (5), Nb/DV (4), Nb/SV (4), Sc/DV (4), Sc/SV (5), Cr/SV (4), Zr/DV (2), Zr/SV (4), Y/SV (5), Ti/SV (4), Mn/SV (3) and Fe/SV (2). For most systems studied, the average adsorption energy decreases as n increases, except for Y/SV and Mn/SV. For these two systems, the adsorption is rather weak, with the average adsorption energy around 0.3 eV, resulting in a rather flat adsorption energy variation with increasing CO₂.

Fig. 3 Average adsorption energies () of CO₂ molecules adsorbed on (a) M/SV and (b) M/DV graphene.

Ca is a non-TM adatom with a remarkably strong CO₂ capture performance, and the capacity to adsorb up to 5 (Ca/SV) and 5 (Ca/DV) CO₂ molecules. Ca-doped CNTs and pristine graphene was investigated in ref. 37. For the purpose of comparison with the results of ref. 37, we consider the adsorption of Ca on pristine graphene in a 72 C atom supercell, and its interaction with a single CO₂ molecule. The binding energy of Ca is −0.81 eV. This value agrees reasonably well with the result of ref. 37 of −1.02 eV (we note that the difference in value may be due to the different sized supercells used: ours contained 72 C atoms, while theirs contained 32 C atoms). However, Ca-doped graphene might not be the best system for sustainable CO₂ capture because of the strong tendency of Ca to leave its vacancy site and bond with an O atom to form CaO clusters, accompanied by the formation of CO gas. This is demonstrated using the following equation,³⁷

Here ΔE^MO is the formation energy if the metal oxide cluster, ΔE^MO₂ is the formation energy of the metal dioxide cluster, E(MO)/E(MO₂) is the total energy of the bulk oxide and E(CO) is the total energy of the CO molecule. The obtained values are ΔE^MO = −0.9 eV for Ca/SV, and ΔE = −1.33 eV for Ca/DV. For comparison, ΔE^MO = +2.45 eV for Nb/SV, ΔE^MO₂ = +1.02 eV for Ti/SV (forming TiO₂), ΔE = +1.29 eV Ti/SV (forming TiO) and ΔE^MO = +0.89 eV for Zr/SV. These positive numbers indicate that TM atoms are more suitable for CCS applications than Ca because the doped graphene system is stable against clustering into its oxide upon CO₂ adsorption. It is worth noting that although the formation energies for Ca/SV and Ca/DV have negative signs, those two structures might still have a potential advantage because CaO + CO₂ → CaCO₃ is a thermodynamically favorable process.³⁸ Therefore, out of the structures with multiple CO₂ capacity, the systems Nb/SV, Nb/DV, Sc/SV, Zr/SV, Y/SV, Ti/SV, Cr/SV and Mn/SV appear to be the most promising candidates for CCS applications as they can bind multiple CO₂ molecules. Interestingly, it can be seen that the elements considered in this study display a trend in their capture capacity (cf. Fig. 1): the capacity roughly increases as we go to the left of the periodic table (except for vanadium) for both first and second row TM elements.

To gain insight into the nature of the bond between CO₂ and the TM/graphene system, the electronic properties of the systems are investigated by studying the density of states (DOS) and partial DOS (pDOS). As an example, we consider Nb/SV, where the results are shown in Fig. 4. The corresponding atomic structure is show in Fig. 4(e). In Fig. 4(a), the total DOS are shown for the Nb/SV structure without CO₂, and in Fig. 4(b) the total DOS with the adsorption of one CO₂ molecule. While pristine graphene is a semimetal, Nb/SV graphene is clearly metallic. When CO₂ bonds to the Nb atom, the O-related 2p states of CO₂ hybridize with the 4d states of the Nb atom, which is the reason for the relatively high adsorption energy. This can be seen from Fig. 4(c) and (d) which show respectively the pDOS for the C and O 2p states of the CO₂ molecule and the 4d states of the Nb adatom for the situation where CO₂ is far (10 Å) from the surface (before bonding) and in the equilibrium geometry (after bonding). Finally, from Fig. 4(c), it can be seen that the two characteristic π_g and π_u peaks of CO₂ (ref. 38) are shifted to higher energy on adsorption. Adsorption of CO₂ also causes the spin-up 4d peak of Nb to move above the Fermi level, and the emergence of a spin-down hybridized Nb-4d–O-2p state (cf. Fig. 4(d)). This indicates that spin-up electrons were transferred from Nb to the CO₂–metal bond. According to Voronoi charge analysis, the free CO₂ molecule accepts −0.27|e|, which means that the CO₂ molecule hole-dopes the Nb/SV system.

Fig. 4 Total and partial DOS (pDOS) for Nb/SV before and after CO₂ adsorption. (a) Total DOS of Nb/SV and (b) total DOS of Nb/SV with a single CO₂ molecule adsorbed, and the pDOS of showing the 4d state of Nb and the 2p-projected states of the O and C atoms of CO₂ for (c) Nb/SV and a non-interacting CO₂ molecule and (d) Nb/SV with a single CO₂ molecule adsorbed, with the atomic structure shown in (e). The pDOS in (c) is obtained for a single CO₂ molecule 10 Å away from the Nb/SV surface.

The magnetization of the different systems is given in Fig. 1 in terms of the total spin magnetic moment of the system before and after adsorption of CO₂. An interesting observation is that CO₂ adsorption affects the magnetic moment of some systems, with the largest magnetic moment change happening in Nb/DV (total quenching of magnetic moment), Fe/SV (87% drop), Co/SV (80% drop) and Ca/DV (50% drop). However, the Fe/DV, Mn/SV and Mn/DV systems, which have the highest magnetic moments (3.76 μ_B, 2.95 μ_B and 3.42 μ_B, respectively), do not undergo any significant change in magnetization. In spite of the high reactivity of Ca/SV towards CO₂, CO₂ only mildly affects its spin. Strong CO₂ capture systems Zr/SV, Zr/DV, Ti/SV and Y/SV are non magnetic, and do not become magnetic upon CO₂ adsorption. The changing of magnetic moments upon CO₂ adsorption highlights the interaction between the adsorbed CO₂ molecules and the dopant–vacancy complexes.

Charge transfer has been a key concept to study the interaction between gas molecules and metallic ions.^18,39 Fig. 5 displays the progressive change of the net charge on the metal dopant relative to the metal without CO₂ present, for increasing numbers of adsorbed CO₂. All of the adatoms in the figure, except Nb/SV system, react to the adsorption of the first CO₂ molecule by gaining electron charge, with less charge gained per CO₂ as more CO₂ molecules are adsorbed. This behaviour is in contrast to the case of hydrogen adsorption, reported in ref. 18, where Ca, Sc, Ti, Y and Zr adsorbed on DV graphene interacts with H₂ molecules by donating charge. Upon adsorption of the first CO₂, the metal dopant in Zr/DV acquires the greatest amount of electron charge (0.256e), followed by the metal dopant in Sc/SV (0.204e), Ti/SV (0.202e), Y/SV (0.191e), and Zr/SV (0.184e), while in the rest of the systems the metal adatom acquire a much smaller amount of electron charge. As the systems reach the maximum capacity, the metal adatom in Y/SV has accumulated the largest amount of charge (0.341e). In spite of displaying greater adsorption energies than other systems, Nb/DV and Nb/SV display only a small net charge transfer. In the Voronoi formalism, the first adsorbed CO₂ in Ca/SV, Ca/DV, Co/SV, Fe/SV, Nb/SV, Nb/DV and Ni/SV receives electrons, whereas the first CO₂ adsorbed on the rest of the systems loses electron charge. All of the aforementioned 7 systems (in addition to Zr/SV) involve the creation of the CO₂ anion (i.e. the bending of the CO₂ molecule, see Sec. 3.3). Upon the adsorption of subsequent CO₂, the nCO₂ complex for these systems donates electron charge to the metal–graphene system.

Fig. 5 Change in the charge of the metal adatom, calculated using the Voronoi method, upon adsorption of additional nCO₂ molecules (a) M/SV and (b) M/DV graphene, relative to the system without CO₂. The negative value of the Voronoi charge change indicates that the metal atom has gained electrons.

The variation of charge on the dopant ion and CO₂ molecules is related to the defective graphene sheet. The charge transfer and redistribution processes among the components of each gas–metal–graphene system exhibits vast diversity, as shown in the schematic diagram in Fig. 6. The diagram shows that the edge C atoms surrounding the defect, as well as the whole graphene sheet, play an important role in the reaction with the adsorbed CO₂ molecules. Before adsorbing the first CO₂, charge has been transferred from the metal adatom to the graphene sheet, mostly into the C_E atoms. Generally, the charge transfer process involved in the adsorption of the first CO₂ is dramatically different from that involved in the adsorption of subsequent CO₂ molecules. The CO₂ complex tends to keep on losing charge, while the graphene sheet tends to keep on attracting charge as more CO₂ molecules are adsorbed. This highlights a novel role of the defective graphene, where it plays the role of a charge reservoir for binding CO₂ molecules. Except for Ca/SV, starting from the second adsorbed CO₂ molecule, the metal acts as a “channel” for charge transfer, where charge passes through the metal from the CO₂ complex to the graphene charge reservoir. In general, SV systems donate more charge to the first adsorbed CO₂ than DV systems.

Fig. 6 Schematic diagram showing, for selected systems, the gain (green triangles pointing upwards) and loss (red triangles pointing downwards) of electron charge density when nCO₂ molecules are adsorbed on metal–DV/SV graphene, for each of the four components: M (the metal adatom), nCO₂ (the whole adsorbed nCO₂ complex), C_E (the edge C atoms, adjacent to the metal adatom) and Gr (the whole graphene sheet, including C_E). For the case of no adsorbed CO₂ molecules, the change in electron density is with respect to the clean defective graphene sheet and the isolated free metal atom. For the case of nCO₂ adsorbed, n ≥ 1, the change is with respect to the (n − 1)CO₂ M/SV graphene system. Yellow circles indicate minimal charge transfer. A series of consecutive yellow circles indicate that the component either does not contribute to the charge transfer mechanism (such as C_E in Sc/SV, starting from the first adsorbed CO₂ molecule) or acts as a channel for charge transfer (such as M in Nb/SV, which does not accumulate significant charge density starting from the first adsorbed CO₂ molecule).

To gain further insight into charge distribution, we plot the density difference (Δρ(r)) distributions for two representative systems, Ca/DV and Sc/SV with five adsorbed CO₂ molecules, in Fig. 7, where Δρ is given by

Here is the charge density of the system M/SV(DV) with nCO₂ molecules adsorbed, ρ_M/SV(DV)Gr is the electron charge density of the M/SV(DV) system with no adsorbed CO₂ molecules, and ρ^nCO₂ is the charge density computed for nCO₂ molecules at the same coordinates as those in the M/SV(DV) system with adsorbed nCO₂ molecules.

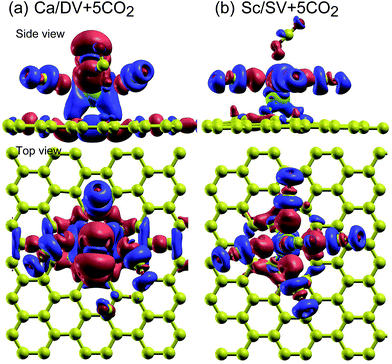Fig. 7 Density difference (Δρ) distributions for (a) Ca/DV and (b) Sc/SV systems, as defined in eqn (5). Δρ > 0 (in blue) indicates a region with electron charge density accumulation, whereas Δρ < 0 (in red) indicates a region with electron charge density depletion. In all cases, the isovalue is 0.001e.

In Fig. 7(a), we can observe that the metal adatom gains charge, which is consistent with the series of green triangles for Ca/DV in Fig. 6. The Sc adatom in the Sc/SV system (Fig. 7(b)) is surrounded by smaller blue and red clouds (small charge densities), corresponding to the series of yellow circles for Sc/SV in Fig. 6. The difference between the two systems is that the graphene sheet is more involved in the electron charge redistribution for Ca/DV than for Sc/SV. An interesting observation in both systems is that the interaction between the adatom and the CO₂ molecule involves a polarization of the CO₂ molecule. This can be seen in Fig. 7 where the oxygen atom of CO₂ closest to the adatom loses charge, while the one further away from the adatom gains charge.

3.3 Formation of bent CO₂ anions

Interestingly, the charge transfer also has an impact on the structure of the first adsorbed CO₂ molecule. The D ∞ h symmetry of CO₂ of the first CO₂ molecule adsorbed to seven of the systems considered, namely Ca, Nb, Co, Ni, Fe, Zr and Y, is broken due to significant metal adatom–CO₂ molecule interaction. This interaction, for Ca, Nb, Co, Ni and Fe, involves considerable charge transfer to CO₂. For these systems, the bending of the CO₂ molecule occurs without an energy barrier. This results in weakened and longer C–O bonding, as well as an unbalanced charge occupation on the two O atoms of the CO₂ molecule. In all of the systems that experience O–C–O bending, the C–O bond length increases from the initial 1.18 Å. The O–C–O angles and C–O bond lengths in the non-collinear cases are: 131.6°, 1.26 Å in Ca/DV, 130.5°, 1.26 Å in Ca/SV, 152.5°, 1.22 Å in Co/SV, 151.6°, 1.23 Å in Nb/DV, 140.9°, 1.29 Å in Nb/SV, 148.6°, 1.26 Å in Ni/SV, 147°, 1.27 Å in Fe/SV, 155.0°, 1.24 Å in Y/SV and 154.2°, 1.25 Å in Zr/DV. These CO₂ anions could potentially react with two protons, to generate a CO and H₂O.²⁶

For the Ca and Nb systems, the first adsorbed CO₂ molecule gains significant electron charge, 0.29e for Ca/DV, 0.34e for Ca/SV, 0.23e for Nb/DV and 0.27e for Nb/SV, which are larger than the respective values in other systems. This explains why the first adsorbed CO₂ for these systems bend by larger angles than the rest of the systems. These two adatoms bond with the three atoms of the first CO₂ molecule. This is reminiscent of the formation of metal carbonates, which are known to form at many metal surfaces.⁴⁰ For the Ni, Co, Zr and Y adatoms, they bond with the C atom of CO₂ and one of the two O atoms. Note that the bending is greatest in the strongest two adsorbents, Ca and Nb, but the angle also significantly changes in the case of a weak adsorbent, namely Ni.

Metal elements embedded in SV and DV graphene have distinct chemical behavior from their bulk counterparts. The formation of nickel carbonate was reported by Freund and Roberts in their experimental review work.⁴⁰ It is interesting to note that some metals that form bulk carbonates in the presence of CO₂ without requiring additional energy, oxidation or catalysis⁴⁰ fail to do so when adsorbed on SV/DV graphene. For example, CO₂ forms a carbonate on the Cu(211) surface, on the Mg(0001) surface and on Al foil.

4 Conclusions

We report a comprehensive first-principles DFT study of multiple CO₂ capture on 16 representative metal-doped graphene systems, for the dopant adsorbed on single and double vacancies (SV and DV, respectively) in graphene. We use a combination of adsorption energy and bond distance criteria to evaluate the CO₂ adsorption capacity. Significantly, our results reveal the dual beneficial roles of vacancies in graphene: (1) to effectively stabilize the adsorbed metal adatom, and (2) to enable defective graphene to act as a charge reservoir for enhancing the CO₂ capture capacity. Generally, SV graphene with metal dopants are better sorbents than DV systems. Importantly, our results predict that each Ca, Sc and Y adatom can capture up to 5 CO₂ molecules. However, in spite of displaying superior capture capacity, Ca systems readily create CaO upon reaction with CO₂, thus rendering Ca/SV and CA/DV graphene less reusable for CO₂ capture. Also interestingly, bent CO₂ anion molecules are predicted for Ca, Nb, Co, Ni, Fe, Zr and Y doped systems. These findings will be useful in the design and optimization of metal-doped graphene systems for energy and environmental applications.

Acknowledgements

This research was undertaken with the assistance of resources from the National Computational Infrastructure (NCI), which is supported by the Australian Government.

References

1. P. Markewitz, W. Kuckshinrichs, W. Leitner, J. Linssen, P. Zapp, R. Bongartz, A. Schreiber and T. E. Muller, Energy Environ. Sci., 2012, 5, 7281–7305.
2. D. M. D'Alessandro, B. Smit and J. R. Long, Angew. Chem., Int. Ed., 2010, 49, 6058–6082.
3. A. Samanta, A. Zhao, G. K. H. Shimizu, P. Sarkar and R. Gupta, Ind. Eng. Chem. Res., 2011, 51, 1438–1463.
4. A. M. Kierzkowska and C. R. Muller, Energy Environ. Sci., 2012, 5, 6061–6065.
5. G. T. Rochelle, Science, 2009, 325, 1652–1654.
6. A. Pulido, M. R. Delgado, O. Bludsky, M. Rubes, P. Nachtigall and C. O. Arean, Energy Environ. Sci., 2009, 2, 1187–1195.
7. D. Britt, H. Furukawa, B. Wang, T. G. Glover and O. M. Yaghi, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 20637–20640.
8. A. K. Mishra and S. Ramaprabhu, J. Mater. Chem., 2012, 22, 3708–3712.
9. J. W. Burress, S. Gadipelli, J. Ford, J. M. Simmons, W. Zhou and T. Yildirim, Angew. Chem., Int. Ed., 2010, 49, 8902–8904.
10. H. Liu, V. R. Cooper, S. Dai and De-en Jiang, J. Phys. Chem. Lett., 2012, 3, 3343–3347.
11. F. Schedin, A. K. Geim, S. V. Morozov, E. W. Hill, P. Blake, M. I. Katsnelson and K. S. Novoselov, Nat. Mater., 2007, 6, 652–655.
12. A. K. Mishra and S. Ramaprabhu, AIP Adv., 2011, 1, 032152.
13. T. Zhang, Q. Xue, M. Shan, Z. Jiao, X. Zhou, C. Ling and Z. Yan, J. Phys. Chem. C, 2012, 116, 19918–19924.
14. Y. Liu and J. Wilcox, Environ. Sci. Technol., 2012, 46, 1940–1947.
15. V. Chandra, S. U. Yu, S. H. Kim, Y. S. Yoon, D. Y. Kim, A. H. Kwon, M. Meyyappan and K. S. Kim, Chem. Commun., 2012, 48, 735–737.
16. Y. Zhao, X. Liu, K. X. Yao, L. Zhao and Y. Han, Chem. Mater., 2012, 24, 4725–4734.
17. G.-P. Hao, Z.-Y. Jin, Q. Sun, X.-Q. Zhang, J.-T. Zhang and A.-H. Lu, Energy Environ. Sci., 2013, 6, 3740–3747.
18. K. M. Fair, X. Y. Cui, L. Li, C. C. Shieh, R. K. Zheng, Z. W. Liu, B. Delley, M. J. Ford, S. P. Ringer and C. Stampfl, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 014102.
19. K. Pi, K. M. McCreary, W. Bao, W. Han, Y. F. Chiang, Y. Li, S. W. Tsai, C. N. Lau and R. K. Kawakami, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 075406.
20. H. Wang, Q. Wang, Y. Cheng, K. Li, Y. Yao, Q. Zhang, C. Dong, P. Wang, U. Schwingenschlgl, W. Yang and X. X. Zhang, Nano Lett., 2011, 12, 141–144.
21. Y. Gan, L. Sun and F. Banhart, Small, 2008, 4, 587–591.
22. J. Dai, J. Yuan and P. Giannozzi, Appl. Phys. Lett., 2009, 95, 232105.
23. Q. Zhao, M. Buongiorno Nardelli, W. Lu and J. Bernholc, Nano Lett., 2005, 5, 847–851.
24. B. Cho, J. Yoon, M. G. Hahm, D.-H. Kim, A. R. Kim, Y. H. Kahng, S.-W. Park, Y.-J. Lee, S.-G. Park, J.-D. Kwon, C. S. Kim, M. Song, Y. Jeong, K.-S. Nam and H. C. Ko, J. Mater. Chem. C, 2014, 2, 5280–5285.
25. A. V. Krasheninnikov, P. O. Lehtinen, A. S. Foster, P. Pyykk and R. M. Nieminen, Phys. Rev. Lett., 2009, 102, 126807.
26. H. He, P. Zapol and L. A. Curtiss, Energy Environ. Sci., 2012, 5, 6196–6205.
27. G. Eranna, B. C. Joshi, D. P. Runthala and R. P. Gupta, Crit. Rev. Solid State Mater. Sci., 2004, 29, 111–188.
28. M. S. Jos, A. Emilio, D. G. Julian, G. Alberto, J. Javier, O. Pablo and S.-P. Daniel, J. Phys.: Condens. Matter, 2002, 14, 2745.
29. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
30. N. Troullier and J. Martins, Solid State Commun., 1990, 74, 613–616.
31. N. Ooi, A. Rairkar and J. B. Adams, Carbon, 2006, 44, 231–242.
32. K. T. Chan, J. B. Neaton and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 235430.
33. J. Lan, D. Cao, W. Wang and B. Smit, ACS Nano, 2010, 4, 4225–4237.
34. X. Y. Cui, R. K. Zheng, Z. W. Liu, L. Li, B. Delley, C. Stampfl and S. P. Ringer, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 125410.
35. C. Fonseca Guerra, J.-W. Handgraaf, E. J. Baerends and F. M. Bickelhaupt, J. Comput. Chem., 2004, 25, 189–210.
36. M. Scheffler and C. Stampfl, in Handbook of Surface Science, Vol. 2: Electronic Structure, ed. K. Horn and M. Scheffler, Elsevier, Amsterdam, 2000, p. 286.
37. C. Cazorla, S. A. Shevlin and Z. X. Guo, J. Phys. Chem. C, 2011, 115, 10990–10995.
38. S. Gudmundsdttir, W. Tang, G. Henkelman, H. Jnsson and E. Sklason, J. Chem. Phys., 2012, 137, 164705.
39. J. Niu, B. K. Rao and P. Jena, Phys. Rev. Lett., 1992, 68, 2277.
40. H. J. Freund and M. W. Roberts, Surf. Sci. Rep., 1996, 25, 225–273.

---