Electronic structure and thermoelectric properties of Zintl compounds A₃AlSb₃ (A = Ca and Sr): first-principles study

Abstract

Experimentally synthesized Zn-doped Sr₃AlSb₃ exhibited a smaller carrier concentration than Zn-doped Ca₃AlSb₃, which induces a lower thermoelectric figure of merit (ZT) than Zn-doped Ca₃AlSb₃. We used first-principles methods and the semiclassical Boltzmann theory to study the reason for this differing thermoelectric behavior and explored the optimal carrier concentration for high ZT values via p-type and n-type doping. The covalent AlSb₄ tetrahedral arrangement exhibited an important effect on the electronic structure and thermoelectric properties. p-type Ca₃AlSb₃ may exhibit good thermoelectric properties along its covalent AlSb₄ chain due to its double band degeneracy at the valence band edge and small effective mass along its one-dimensional chain direction. Zn doping the Al site exhibited higher formation energy for Sr₃AlSb₃ than Ca₃AlSb₃, which explains the lower carrier concentration for Zn-doped Sr₃AlSb₃ than Zn-doped Ca₃AlSb₃. The double band degeneracy at the valence band edge for Ca₃AlSb₃ may also help to increase the carrier concentration. Sr₃AlSb₃ containing isolated Al₂Sb₆ dimers can exhibit a high thermoelectric performance via heavy p-type doping with a carrier concentration above 1 × 10²⁰ holes per cm³. Moreover, the ZT maxima for the n-type Sr₃AlSb₃ can reach 0.76 with a carrier concentration of 4.5 × 10²⁰ electrons per cm³.

---

I. Introduction

Thermoelectric materials can convert energy between heat and electricity and have attracted significant attention. The conversion efficiency for thermoelectric materials is defined by the dimensionless figure of merit, ZT = S²σT/κ, where S, σ, T, and κ are the Seebeck coefficient, electrical conductivity, absolute temperature, and thermal conductivity, respectively. Therefore, a promising thermoelectric material should have a large Seebeck coefficient, high electrical conductivity, and low thermal conductivity. However, S, σ, and κ are always coupled, which makes it difficult for a material to simultaneously have high S, high σ, and low κ.¹ The concept of a “phonon glass electron crystal” (PGEC) is a good approach for achieving good thermoelectric performance.² Materials with complex structures often have low intrinsic lattice thermal conductivities and may have good thermoelectric properties.^3,4 Zintl compounds have emerged as a promising class of materials for thermoelectric applications due to their complex crystal structures^5,6 and low intrinsic lattice thermal conductivity. For example, the lattice thermal conductivities of Ca₃AlSb₃, Sr₃AlSb₃, and Sr₃GaSb₃ are below 0.6 W mK⁻¹ at 1000 K.^4,7,8

Finding cheap, nontoxic thermoelectric materials with high conversion efficiencies is important.⁹ Ca₃AlSb₃ and Sr₃AlSb₃ are promising compounds for thermoelectric applications due to their earth abundant, nontoxic elemental composition. The transport properties for Ca₃AlSb₃ and Zn-doped Ca₃AlSb₃ were experimentally investigated,^4,10 and the thermoelectric properties of Ca₃AlSb₃ were improved via p-type doping to obtain a maximum ZT = 0.8 at 1050 K.¹⁰ Sr₃AlSb₃ exhibits a maximum ZT value of 0.1 at 1000 K. Zinc doping has little effect on the carrier concentration in Sr₃AlSb₃ and does not improve the ZT.⁷ Comparing the properties for Ca₃AlSb₃ and Sr₃AlSb₃ ref. 4, 7 and 10 reveals an interesting phenomenon: Zn-doped Sr₃AlSb₃ exhibits a lower carrier concentration than Zn-doped Ca₃AlSb₃ with a maximum ZT value of approximately 0.15 at 800 K.⁷ Such a low carrier concentration could cause the low ZT for Sr₃AlSb₃. Hence, improving the low Sr₃AlSb₃ carrier concentration is important to improve its thermoelectric performance. Carrier concentrations always exhibit opposing effects on S, σ, and κ_e. Thus, optimizing the carrier concentration can increase the ZT values for Ca₃AlSb₃ and Sr₃AlSb₃. To explain these phenomenon and improve the thermoelectric properties, we calculated the electronic structures and thermoelectric properties for A₃AlSb₃ (A = Ca, Sr) using a first-principles method and the semiclassical Boltzmann theory. We found that p-type Ca₃AlSb₃ is a promising thermoelectric compounds along the chain direction. Meanwhile, n-type and p-type Sr₃AlSb₃ may also have good thermoelectric properties via heavy doping.

II. Computational detail

Experimental A₃AlSb₃ (A = Ca, Sr) structures are used as the initial bulk model and relaxed to obtain the minimum energy structure.^11,12 The structure was optimized using the projector-augmented-wave (PAW) method based on density functional theory (DFT) as implemented in Vienna ab initio simulation package (VASP).^13–15 The exchange-correlation function was treated with the Perdew–Burke–Ernzerhof (PBE) generalized-gradient approximation (GGA).^16–18 A plane wave cutoff energy of 500 eV was used throughout. For the Brillouin zone integration, 4 × 11 × 3 and 2 × 7 × 4 Monkhorst-Pack special k-point grids were used for Ca₃AlSb₃ and Sr₃AlSb₃, respectively.

We calculated the electronic structure via the full-potential linearized augmented plane waves (FLAPW) method¹⁹ implemented in WIEN2k.^20–22 The exchange-correlation potential was below the generalized gradient approximation (GGA) as parameterized by Perdew, Burke, and Ernzerhof (PBE).¹⁶ A plane wave basis cutoff of R_mtK_max = 8 was used. The muffin tin radius was 2.5 a.u. for Ca, Sr, Al, and Sb. Self-consistent calculations were performed using 500 k points in the irreducible Brillouin zone for both Ca₃AlSb₃ and Sr₃AlSb₃. We obtained accurate band gaps using the modified Becke–Johnson (TB-mBJ)²³ semilocal exchange potential, and the TB-mBJ method reliably predicted the band gap for sp-bonded semiconductors.²⁴ We included the scalar-relativistic and spin–orbit coupling effects (RSO) to account for Sr due to its large atomic mass.

The thermoelectric properties were evaluated via the semiclassical Boltzmann theory^25–27 as implemented in the Boltz-Trap code.²⁸ The constant scattering time approximation was used, assuming that the scattering time determining the electrical conductivity does not vary significantly with energy on the scale of kT.

III. Results and discussions

A. Crystal structure and properties

Two structure types were formed in the A₃AlSb₃ compounds (A = alkaline earth metals): Ca₃InP₃ (no. 62 Pnma) and Ba₃AlSb₃ (no. 64 Cmca). The tetrahedral A₃AlSb₃ (A = Ca, Sr) structures determined by our simulations are shown in Fig. 1. The figure does not show the A site atoms to better show the tetrahedral AlSb₄ arrangement. The Ca₃AlSb₃ had an anisotropic one-dimensional structure that formed a Ca₃InP₃ structure from infinite chains of corner-sharing tetrahedral AlSb₄ linked by Ca ions.²⁹ Sr₃AlSb₃ formed a Ba₃AlSb₃ structure type. The Al₂Sb₆¹²⁻ dimer in Sr₃AlSb₃ are shown in Fig. 1 and formed from two tetrahedral sharing a common edge as for Al₂Cl₆. Meanwhile, Sr and Sb formed a distorted NaCl-type arrangement with Al in tetrahedral holes.

Fig. 1 The tetrahedral structure of A₃AlSb₃ (A = Ca, Sr) with space group Pnma, and Cmca, respectively. The blue and brown spheres represent Al and Sb atoms, respectively.

The optimized structure parameters and bond lengths are listed in Tables 1 and 2. The lattice constants and atomic positions of the optimized structures are close to the experimental values.^11,12 The bond lengths between Al and the neighboring Sb atoms in A₃AlSb₃ (A = Ca, Sr) were 2.73 Å, and 2.71 Å, respectively. That is, Sr₃AlSb₃ may have stronger Al–Sb interactions than Ca₃AlSb₃. In addition, Table 1 indicates each Ca₃AlSb₃ primitive cell contained seven inequivalent atoms, and each Sr₃AlSb₃ one contained five inequivalent atoms. However, each Sr₃AlSb₃ primitive cell had 56 atoms in common with Sr₃GaSb₃, while each Ca₃AlSb₃ cell had only 28 atoms in common. This complex structure suggests Sr₃AlSb₃ should have a lower lattice thermal conductivity (approximately 0.55 W mK⁻¹ at 1000 K) than Ca₃AlSb₃ (approximately 0.60 W mK⁻¹ at 1000 K). The large cell and complex structure always induce short mean-path-lengths of heat carrying phonons.³⁰

Table 1 Calculated lattice parameters and fractional atomic coordinated for Wyckoff sites of optimized A₃AlSb₃ (A = Ca, Sr)

Lattice parameter	Atomic type	Wyckoff symbol	x	y	z
Orthorhombic	Ca1	4c	0.27240	0.25000	0.27952
No. 62 Pnma	Ca2	4c	0.55863	0.25000	0.38798
a = 12.9637 Å	Ca3	4c	0.35002	0.25000	0.99673
b = 4.5191 Å	Al	4c	0.56762	0.25000	0.79666
c = 14.3421 Å	Sb1	4c	0.61368	0.25000	0.60928
	Sb2	4c	0.75644	0.25000	0.88129
	Sb3	4c	0.04036	0.25000	0.35077
Orthorhombic	Sr1	8f	0.17600	0.30314	0.12913
No. 64 Cmca	Sr2	16g	0.00000	0.19028	0.35367
a = 20.6293 Å	Al	8d	0.08617	0.00000	0.00000
b = 6.9666 Å	Sb1	8f	0.33948	0.28833	0.12283
c = 13.6355 Å	Sb2	16g	0.00000	0.21262	0.10750

---

Table 2 Calculated bond distances (in Å) of optimized A₃AlSb₃ (A = Ca, Sr)

Atomic type			Nearest neighbor table
Ca1	Sb1 3.14	Sb3 3.18	Sb2 3.25	Al 3.26
Ca2	Sb1 3.18	Sb1 3.25	Sb2 3.30
Ca3	Sb2 3.17	Sb3 3.30	Sb3 3.39	Sb1 3.42
Al	Sb2 2.73	Sb1 2.75	Sb3 2.77	Ca1 3.26
Sb1	Al 2.75	Ca1 3.14	Ca2 3.18	Ca2 3.25
Sb2	Al 2.73	Ca3 3.17	Ca1 3.25	Ca2 3.30
Sb3	Al 2.77	Ca1 3.18	Ca3 3.30	Ca3 3.39
Sr1	Al 3.32	Sb1 3.38	Sb1 3.40	Sb1 3.51	Sb1 3.60	Sb2 3.70
Sr2	Sb2 3.36	Sb2 3.37	Sb1 3.40	Sb1 3.40	Al 3.43	Al 3.43
Al	Sb1 2.71	Sb1 2.71	Sb2 2.74	Sb2 2.74	Sr1 3.32	Sr1 3.72
Sb1	Al 2.71	Sr1 3.38	Sr1 3.40	Sr2 3.40	Sr1 3.40
Sb2	Al 2.74	Al 2.74	Sr2 3.36	Sr2 3.37

---

Previous experimental work by Zevalkink et al. found Zn-doped Sr₃AlSb₃ possessed a lower carrier concentration than Zn-doped Ca₃AlSb₃.^4,7,10 To explain the low carrier concentration in Sr₃AlSb₃, we calculated the formation energies (E_f) for A₃AlSb₃ (A = Ca, Sr) using a Y atom to replace X (X = Ca, Sr, Al, Sb, Si, Ge, or Sn) in the 1 × 4 × 1 and 1 × 2 × 1 supercell. The formation energy was calculated using

E_f = E_doped − E_bulk − E_X + E_Y, (1)

where, E_doped and E_bulk are the total energies for the supercell containing the substitutional dopant Y and the same bulk A₃AlSb₃ supercell, respectively. E_Y and E_X are the doping and host atom energies in the bulk phase. The calculated formation energies are shown in Table 3. First, Zn more easily replaces Al than Sb. Second, Zn more easily dopes in the Al site in Ca₃AlSb₃ than Sr₃AlSb₃, possibly due to the stronger bond between Al and Sb in Sr₃AlSb₃. Therefore, Zn-doped Sr₃AlSb₃ has a lower carrier concentration than Zn-doped Ca₃AlSb₃, as reported in ref. 4, 7 and 10. Third, the formation energy for doping the A site is lower for K than Na, which was probably due to K exhibiting a stronger activity than Na. Lastly, the A (A = Ca, Sr) site atom is easier to replace in Ca₃AlSb₃ than Sr₃AlSb₃. n-type doping for Ca₃AlSb₃ and Sr₃AlSb₃ has never been performed experimentally. It is interesting to explore the possibility of n-type doping in these two compounds. Thus, we also calculated the formation energies of Si, Ge, and Sn on Al sites. As shown in Table 3, doping of Sn on Al sites is most easily performed in Ca₃AlSb₃, and doping of Ge in Al site is most easily performed in Sr₃AlSb₃ among Si, Ge, and Sn elements. The calculated formation energies shows that doping of Si, Ge, and Sn on Al site are more difficult than that of Zn on Al site.

Table 3 Calculated formation energies (in eV) of A₃AlSb₃ (A = Ca, Sr) by using Y atoms to replace X atoms

	X = A, Y = Na	X = A, Y = K	X = Al, Y = Zn	X = Sb, Y = Zn
Ca3AlSb3	1.23	0.77	0.06	2.1
Sr3AlSb3	1.67	1.63	0.24	2.3

---

	X = Al, Y = Si	X = Al, Y = Ge	X = Al, Y = Sn
Ca3AlSb3	1.13	0.79	0.68
Sr3AlSb3	1.05	0.8	0.9

---

B. Transport properties

To optimize the carrier concentration and increase the thermoelectric performance for A₃AlSb₃ (A = Ca, Sr), we calculated the A₃AlSb₃ (A = Ca, Sr) transport coefficients for carrier concentrations from 1 × 10¹⁸ to 1 × 10²² cm⁻³ using the semiclassical Boltzmann theory without considering the special dopant type. Fig. 2 shows calculated transport coefficient results for n-type and p-type A₃AlSb₃ (A = Ca, Sr) at 850 K. Fig. 2(a) shows that the Seebeck coefficients increase and then decrease with increasing carrier concentration. This phenomenon for the Seebeck coefficient at high carrier concentrations can be explained using eqn (2). For degenerate semiconductors, the Seebeck coefficient is given bywhere k_B is the Boltzmann constant, m^*_DOS is the density of states effective mass, T is the temperature, and n is the carrier concentration. The Seebeck coefficients for Sr₃AlSb₃ are larger at low doping concentrations than for Ca₃AlSb₃ mainly due to the larger band gap (S_max = E_g/(2eT_max)). The Seebeck coefficients for p-doped A₃AlSb₃ are slightly larger than when n-doped due to the slightly larger density of states effective mass. Fig. 2(b) shows the electrical conductivities of A₃AlSb₃ (A = Ca, Sr) as a function of carrier concentration. This figure shows that the electrical conductivities increase with increasing carrier concentration regardless the doping type, which is indicative of thermal carrier activation across the band gap and supports the electrical conductivity being proportional to the carrier concentration (σ = neη). The electrical conductivity for n-type Ca₃AlSb₃ first increased and then decreased. The σ is much larger for Ca₃AlSb₃ than Sr₃AlSb₃ due to its smaller band mass m^*_b and one-dimensional chain structure. The σ of A₃AlSb₃ is larger for n-doping than p-doping mainly due to the smaller band mass at the bottom of conduction bands than that at the top of valence bands. Fig. 2(c) shows the ZT as a function of carrier concentration. We find the ZT of Sr₃AlSb₃ was larger for n-type doping than p-type doping due to the higher electrical conductivity. The maximum ZT for n-type Sr₃AlSb₃ reached 0.76, which corresponds to a carrier concentration of 4.5 × 10²⁰ e cm⁻³ and is almost equal to the maximum experimental ZT for p-type Ca₃AlSb₃ (0.8 at 1050 K).

Fig. 2 Calculated transport properties of A₃AlSb₃ (A = Ca, Sr): (a) Seebeck coefficients; (b) electrical conductivities; (c) Z_eT.

It is well known that materials with good thermoelectric properties often have a high anisotropy in their crystal structures.³¹ We determined the best transport direction for A₃AlSb₃ (A = Ca and Sr) using the calculated anisotropic transport coefficients for p-type and n-type A₃AlSb₃ (A = Ca, Sr) as a function of the carrier concentration from 1 × 10¹⁸ to 1 × 10²¹ cm⁻³ along the x, y, and z directions at 850 K, without considering special dopants as shown in Fig. 3. This figure shows the anisotropy of the thermoelectric properties was stronger for Ca₃AlSb₃ than Sr₃AlSb₃ due to its band mass anisotropy in different directions and one-dimensional chain in Ca₃AlSb₃. For Ca₃AlSb₃, both the Seebeck coefficient and σ/τ were higher along the y direction than the x and z directions. This phenomenon is consistent with a one-dimensional chain feature along the y direction in Ca₃AlSb₃

Fig. 3 Calculated anisotropy of thermoelectric properties of Ca₃AlSb₃ (left) and Sr₃AlSb₃ (right) as a function of carrier concentration from 1 × 10¹⁸ to 1 × 10²¹ cm⁻³ along the x, y, and z directions at 850 K.

C. Electronic structure

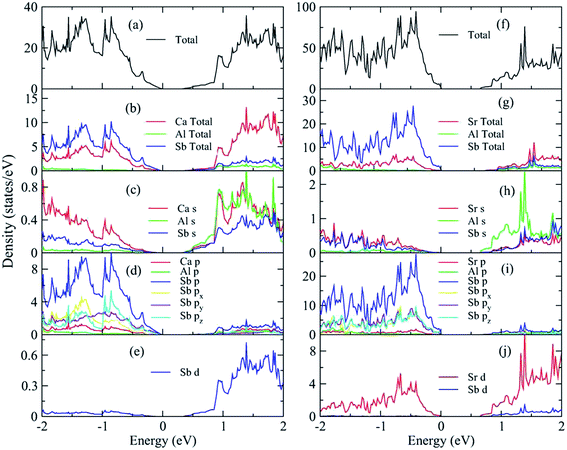
The basic bonding features are reflected in the calculated density of states (DOS) for A₃AlSb₃ (A = Ca, Sr) for energies ranging from −2 eV to 2 eV, as shown in Fig. 4. The Ca or Sr cations mainly contribute to the A₃AlSb₃ conduction bands, the top valence bands are dominated by the Sb states, and the Al states appear in both the valence and conduction band edges. The valence band maxima (VBM) is dominated by Sb p states, likely due to non-bonding Sb lone-pairs. The conduction band minimum (CBM) is dominated by the s and d orbitals. As shown in Fig. 4(c) and (h), the Al s states are dominant at the bottom of conduction band. Fig. 4(d) and (i) show the Sb p states contributions exceed the A p states and Al p states. For Ca₃AlSb₃, the Sb p states differ along the x, y, and z directions. In contrast, the Sb p states for Sr₃AlSb₃ were almost identical in the three directions, which indicates a strong hybridization between the Sb p_x, p_y and p_z.

Fig. 4 Calculated total and partial DOS for A₃AlSb₃ (A = Ca, Sr). The Fermi level is at zero.

The calculated band structures for A₃AlSb₃ (A = Ca, Sr) are depicted in the high symmetry directions in Fig. 5, and the corresponding special k points are shown in Fig. S1, ESI.† The direct band gap is located at the Γ point for both compounds. There are two bands at the band edge for the upper valence bands. For Ca₃AlSb₃, the two bands at Γ and X are degenerate with a large dispersion. However, the two bands for Sr₃AlSb₃ are not strictly degenerate and have a relative small dispersion. Moreover, the two bands at X split in Sr₃AlSb₃. The difference in the band structures for these two compounds arises from their different polyanionic tetrahedral arrangements. For Ca₃AlSb₃, the edge-sharing anionic tetrahedra form one-dimensional chains. However, for Sr₃AlSb₃, the two edge-sharing tetrahedral form isolated Al₂Sb₆ dimers. The one-dimensional covalent chain feature enhance the covalency degree in the chain direction with a small induced band effective mass in Ca₃AlSb₃. Consequently, Ca₃AlSb₃ exhibits a larger band dispersion in the upper valence bands and lower conduction bands than Sr₃AlSb₃. The carrier mobility determined by A. Zevalkink^4,7 confirmed this prediction.

Fig. 5 Calculated band structures of Ca₃AlSb₃ (left panel) and Sr₃AlSb_s (right panel). The high symmetry k points Γ, X, Y, Z, S, U, and R represent the points (0, 0, 0), (0.5, 0, 0), (0, 0.5, 0), (0, 0, 0.5), (0, 0.5, 0.5), (0.5, 0.5, 0), and (0.5, 0.5, 0.5), respectively.

The carrier effective mass always exhibits opposing effect on the Seebeck coefficient and carrier mobility. A heavy density-of-states effective mass (m^*_DOS) yields a high Seebeck coefficient, and a high mobility always requires a light inertial effective mass (m^*_I) in the transport direction. The m^*_DOS, which is determined by the band mass and band degeneracy (N_v), can be defined as

m^*_DOS = (m^*_xm^*_ym^*_z)^1/3N_v^2/3, (3)

where m^*_x, m^*_y, and m^*_z are the band mass components along the three perpendicular directions x, y, and z, respectively. Fig. 5 and Table 4 show that A₃AlSb₃ band gaps are 0.71 eV and 0.89 eV, which are close to the experimental values of 0.65 eV and 0.70 eV, respectively. The m^*_Γ–X, m^*_Γ–Y, and m^*_Γ–Z for the p-type Ca₃AlSb₃ are lower than for the p-type Sr₃AlSb₃, which corresponds to the higher carrier mobility in the p-type Ca₃AlSb₃. However, the m^*_DOS for the p-type Ca₃AlSb₃ were almost equal to those for p-type Sr₃AlSb₃ due to the double band degeneracy (N_v = 2) at the valence band edge for Ca₃AlSb₃. These results are consistent with the experimental Seebeck coefficient being slightly smaller for p-type Ca₃AlSb₃ than p-type Sr₃AlSb₃. For thermoelectric materials with carriers scattered mainly by acoustic phonons, a light band mass induces a high carrier mobility and improves the thermoelectric performance, which exceeds the detrimental effects on Seebeck coefficient due to the low effective mass.³² Thus, Ca₃AlSb₃ is a promising thermoelectric material.

Table 4 Calculated electronic properties of A₃AlSb₃: band gap (E_g in eV); band degeneracy (N_v); the band mass along three perpendicular directions (m* in m_e); and density of states effective mass (m^*_DOS in m_e)

	Eg (eV)	Nv	m^*Γ–X	m^*Γ–Y	m^*Γ–Z	m^*DOS
n-type Ca3AlSb3	0.71	1	0.67	0.12	0.91	0.42
p-type Ca3AlSb3	0.71	2	0.67	0.57	0.62	0.98
n-type Sr3AlSb3	0.85	1	0.51	0.36	0.78	0.52
p-type Sr3AlSb3	0.85	1	0.87	0.85	1.31	0.99

---

The optimal electronic performance for a thermoelectric semiconductor depends on its weighted mobility,^2,33,34 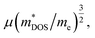where μ and m_e are the carrier mobility and electron mass, respectively. Charge carriers predominantly scattered by acoustic phonons (as occurs in most good thermoelectric materials) are expected to have . Therefore, increasing the band mass should decrease the mobility. However, multiply degenerate valleys produce large m^*_DOS without explicitly reducing μ. A large valley degeneracy of N_v can increase m^*_DOS to yield a large Seebeck coefficient. Thus, a large valley degeneracy is helpful for thermoelectric materials.^35,36 A thermoelectric material with a large N_v may simultaneously have light bands (small m_i) and large m^*_DOS. The N_v for Ca₃AlSb₃ and Sr₃AlSb₃ are 2 and 1, respectively. The contribution from other bands in heavily doped Sr₃AlSb₃ with maxima at approximately −0.1 eV could potentially lead to an N_v of 2, which corresponds to a carrier concentration of 1 × 10²⁰ cm⁻³. Thus, a heavily p-type doped Sr₃AlSb₃ may exhibit better thermoelectric properties at carrier concentrations above 1 × 10²⁰ cm⁻³.

IV. Conclusion

In summary, the structural, thermoelectric, and electronic properties for A₃AlSb₃ (A = Ca, Sr) were studied using the first-principles calculations and semiclassical Boltzmann theory. We found the different thermoelectric properties for Ca₃AlSb₃ and Sr₃AlSb₃ were mainly derived from their different AlSb₄ tetrahedral arrangement. The one-dimensional AlSb₄ chain in Ca₃AlSb₃ yields a stronger anisotropy in the thermoelectric properties than for Sr₃AlSb₃ with isolated Al₃Sb₆ dimers. On the one hand, the one-dimensional chain structure for Ca₃AlSb₃ exhibited high electrical conductivities along the chain direction. On the other hand, the double band degeneracy at the valence band edge creates a large Seebeck coefficient for p-type Ca₃AlSb₃. Consequently, Ca₃AlSb₃ may exhibit good thermoelectric properties along the chain direction, which requires further research experiment. The formation energies calculated for Zn doped at Al sites revealed the origin of lower carrier concentrations of Zn-doped Sr₃AlSb₃ than Zn-doped Ca₃AlSb₃ as reported by experimental workers. The transport properties for Sr₃AlSb₃ indicate the highest achievable ZT for n-type Sr₃AlSb₃ was 0.76, which corresponds to a carrier concentration of 4.5 × 10²⁰ cm⁻³.

Acknowledgements

This research was sponsored by the National Natural Science Foundation of China (No. 51371076 and U1204112), the Program for Innovative Research Team (in Science and Technology) in University of Henan Province (No. 13IRTSTHN017).

References

1. G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105.
2. G. A. Slack, CRC Handbook of Thermoelectrics, ed. D. M. Rowe, CRC, Boca Raton, FL, 1995, pp. 406–440.
3. Y. L. Yan and Y. X. Wang, J. Mater. Chem., 2011, 21, 12497–12502.
4. A. Zevalkink, E. S. Toberer, W. G. Zeier, E. Flaage-Larsen and G. J. Snyder, Energy Environ. Sci., 2011, 4, 510.
5. S. M. Kauzlarich, S. R. Brown and G. J. Snyder, Dalton Trans., 2007, 2099.
6. E. S. Toberer, A. F. May and G. J. Snyder, Chem. Mater., 2010, 22, 624.
7. A. Zevalkink, G. Pomrehn, Y. Takagiwa, J. Swallow and G. J. Snyder, ChemSusChem, 2013, 6, 2316.
8. Q. F. Shi, Y. L. Yan and Y. X. Wang, Appl. Phys. Lett., 2014, 104, 012104.
9. L. E. Bell, Science, 2008, 321, 1457.
10. W. G. Zeier, A. Zevalkink and G. J. Snyder, J. Mater. Chem., 2010, 22, 624.
11. G. Cordier, M. Stelter and H. J. Schaefer, J. Less-Common Met., 1984, 98, 285.
12. G. Cordier, G. Savelsberg and H. Z. Schaefer, Z. Naturforsch., B: J. Chem. Sci., 1982, 37, 975.
13. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558.
14. G. Dresse and J. Hafner, J. Phys.: Condens. Matter, 1994, 6, 8245.
15. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
16. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
17. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
18. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
19. D. Singh, Planewaves, Pseudopentials, and the LAPW Method, Kluwer Academic, Boston, 1994.
20. D. D. Koelling and B. N. Harmon, J. Phys. C: Solid State Phys., 1977, 10, 3107.
21. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, 864.
22. P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka and J. Luitz, WIEN2K, An Augmented Plane Wave+Local Orbitals Program for Calculating Crystal Properties, Vienna University of Technology, Vienna, Austria, 2001.
23. F. Tran and P. Blaha, Phys. Rev. Lett., 2009, 102, 226401.
24. D. Koller, F. Tran and P. Blaha, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195134.
25. J. M. Ziman, Electrons and Phonons, Oxford University Press, New York, 2001.
26. W. Jone and N. H. March, Theoretical Solid State Physics, Courier Dover, New York, 1985.
27. G. K. H. Madsen, K. Schwarz, P. Blaha and D. J. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 125212.
28. T. Thonhauser, T. J. Scheidemantel, J. O. Sofo, J. V. Badding and G. D. Mahan, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 085201.
29. G. Cordier, H. Schaefer and M. Stelter, Z. Naturforsch., B: J. Chem. Sci., 1984, 37, 975.
30. J. R. Sootsman, D. Y. Chung and M. G. Kanatzidis, Angew. Chem., Int. Ed., 2009, 48, 8616.
31. T. J. Scheidemantel, C. Ambrosch-Draxl, T. Thonhauser, J. V. Badding and J. O. Sofo, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 125210.
32. Y. Pei, A. D. Lalonde, H. Wang and G. J. Snyder, Energy Environ. Sci., 2012, 5, 7963.
33. G. D. Mahan, Solid State Physics, Academic Press Inc, San Diego, 1998, vol. 51, p. 81.
34. H. J. Goldsmid, Thermoelectric Refrigeration, Plenum, 1964.
35. F. J. DiSalvo, Science, 1999, 285, 703.
36. Y. Pei, X. Shi, A. LaLonde, H. Wang, L. Chen and G. J. Snyder, Nature, 2011, 473, 66.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra09804a

---