Composition-dependent association behavior in the mixture of isopropanol and trichloromethane: a volumetric, vibration spectroscopic and quantum chemical study†
Abstract
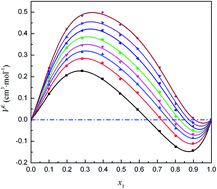
Herein the intermolecular associative behaviors in the binary mixture of isopropanol and trichloromethane have been studied via a combined excess volumetric, vibration spectroscopic and quantum chemical approach. The densities of the mixture studied were obtained at T = (283.15 to 323.15) K and at atmospheric pressure. From the experimental data, the excess molar volumes were obtained as a function of composition, and their corresponding fitted curves show a distinct sigmoidal feature at each temperature, which can be considered in terms of free packing effects and the presence of competition between intermolecular self- and cross-associated interactions. Meanwhile, the composition-dependent association behavior was further ascertained via vibration spectroscopic technology. In addition, the geometric structures, interaction energies, electron topology properties and Gibbs free energy changes of the self- and cross-associations in the mixture studied were investigated via quantum chemical calculations. The computational results have also been interpreted in terms of the composition-dependent association behavior in the mixture studied.

 Please wait while we load your content...
Please wait while we load your content...