Hold-up and flooding characteristics in a perforated rotating disc contactor (PRDC)

Abstract

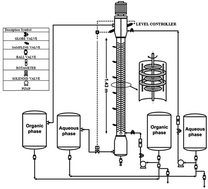
Dispersed phase hold-up and flooding behavior were investigated in a pilot plant scale perforated rotating disc contactor (PRDC) using three different liquid–liquid systems. The influence of various operational parameters including rotor speed, continuous and dispersed phases flow rates on flooding velocities and hold-up have been studied. Changes in the continuous phase velocity has a minor effect on dispersed phase hold-up while increasing dispersed phase flow rate and rotor speed results in an increase in dispersed phase hold-up. Moreover, based on physical properties of liquid systems and operating conditions two empirical correlations were derived for the flooding point and dispersed phase hold-up. The proposed empirical correlations are then validated through comparing with experimental data. Therefore, due to a lack of experimental data on this type of column, these predictive empirical correlations can be used for accurate design of perforated rotating disc contactor.

---

1. Introduction

Solvent extraction (liquid–liquid extraction) has become one of the key unit operations in process industries for many years. This separation process consists in extraction of one or several components from an aqueous phase by addition of a non-miscible or partially miscible liquid phase (organic phase), in which the solute is preferentially dissolved. This separation process is often operated in continuous state in various kinds of extraction columns with different internal structure such as various types of plates, packing, baffles, etc. Two immiscible liquid phases enter the extraction column counter currently, one being dispersed into the other. The duty of the extraction column is to produce a larger interfacial area often via using mechanical agitation to better disperse the phases.^1–4 Agitated extractors such as the rotating disc contactor (RDC) are highly efficient and have suitable operational flexibility in comparison to the conventional packed, sieve and spray extraction column. These advantages have led to the widespread use of the RDC extractor in many industrial separation processes containing oil, food, petroleum and hydrometallurgical, chemical, pharmaceutical and environmental, industries.^5,6 A great deal of studies were conducted on design and operational features of the RDC such as mass transfer performance, slip velocity and dispersed phase hold-up.^7–9 Adapted versions of the RDC including the open turbine rotating disc contactor (OTRDC),^10,11 the asymmetric rotating disc contactor (ARDC),¹² and the perforated rotating disc contactor (PRDC)^13–16 were also developed. The advantages of the perforated rotating disc contactor are producing narrower drop size distributions, higher energy dissipation and higher controllability than that of the RDC.^17,18 However, there is very little reliable information about mass transfer and hydrodynamic behavior of adapted RDC extractors.

Apart from the mass transfer performance in the design and construction of extractor, the hydrodynamic parameters such as dispersed phase hold-up and flooding velocities are vital operational parameters for calculation of the extractor capacity and the extractor diameter. These important variables are needed for determination of desired throughput within the operating range.¹⁹ Furthermore, it is impossible to raise the flow rate of the two phases indefinitely. It is because there is a restriction on the amount of one phase which can be dispersed into the second phase. When the amount of flow rate become more than this restriction value, dispersed phase droplets can no longer fall or rise oppose to the flow of the continuous phase and stable extraction column operation is impossible to achieve. Thus, the maximum volumetric capacity of an extraction column, or flooding throughput as the fundamental question should be taken in account in design of an extractor.²⁰ Column diameter can be determine using the knowledge of the column flooding characteristics by assuming operating loads as a fraction of flooding throughput or via considering the operating hold-up value as a fraction of the dispersed phase volume at flooding condition.^21–23

Little information has appeared in the literature regarding the performance of perforated rotating disc contactor. Thus, for the purpose of the establishing proper design procedures for perforated rotating disc contactor, there is a requirement for appropriate correlations of flooding velocity and dispersed phase hold-up as a function of operating conditions and the physical properties of the liquid phases. The aim of current study is an investigation of dispersed phase hold-up and flooding velocity of a perforated rotating disk contactor as a function of rotor speed, phase flow rates and the physical properties with three different systems. Two empirical correlations are proposed for estimation of dispersed phase hold-up and flood point.

2. Experimental

2.1. PRDC pilot scale unit

A pilot scale perforated rotating disc contactor with a 113 mm internal diameter perforated and 43 stages and its accessories including storage tanks, pumps and rotameters was used in these experiments. The rotor shaft holds up perforated disc with a diameter of 0.07 m and drilled with 30 holes of 0.015 cm diameter. Fig. 1 shows a schematic flow diagram of the experimental equipment. The main dimensions of the PRDC column are illustrated in Table 1.

Fig. 1 A schematic diagram of the perforated rotating disc contactor (PRDC).

Table 1 The main dimensions of the PRDC column

Item	Symbol	Column dimensions (m)
Column internal diameter	Dc	0.113
Stator ring diameter	Ds	0.08
Disc diameter	D	0.07
Compartment height	hc	0.03
Column active height	Z	1.43

---

2.2. Liquid–liquid systems

The liquid–liquid systems investigated were butanol–water (low interfacial tension), n-butyl acetate–water (medium interfacial tension), and toluene–water (high interfacial tension). Due to covering a broad range of interfacial tension values these systems were selected based on recommendations of the European Federation of Chemical Engineering.²⁴ Technical grade of toluene, n-butyl acetate, and butanol were used as dispersed phase and distilled water was used as continuous phase. All experiments were carried out in the absence of mass transfer at room temperature. The physical properties of these systems are provided in Table 2.

Table 2 Physical properties of systems investigated at 20 °C (ref. 24)

Physical property	Toluene–water	n-Butylacetate–water	n-Butanol–water
ρc (kg m^−3)	998.2	997.6	985.6
ρd (kg m^−3)	865.2	880.9	846
μc (mPa s)	0.963	1.0274	1.426
μd (mPa s)	0.584	0.734	3.364
σ (mN m^−1)	36	14.1	1.75

---

2.3. Experimental procedures

Before starting each experiment, the aqueous and organic phases were mutually saturated. The presented physical properties are in saturation state and 20 °C which are provide in Table 1. In order to prevent from changing physical properties room temperature is kept at 20 °C by air conditioners. The column was filled with the continuous phase and the speed of rotor is then adjusted to the certain amount. Next, the dispersed phase was entered into the column. Optical sensor was used to maintain the interface position at the desired height. The system was permitted to reach steady state condition which usually necessitated changing four or five of the column volume. At the end of each run, displacement method is applied to calculate hold-up of dispersed phase in the PRDC extractor.²⁵ The hold-up is the ratio of volume fraction of dispersed phase to volume fraction of dispersed and continuous phases. It may be written using following equation:where v_d represents the volume of the dispersed phase and v_e the total volume of the two phases for the effective length of the column. Flooding velocity is the dispersed phase velocity at which the flooding occurred.

3. Results and discussion

3.1. Dispersed phase hold-up

Dispersed phase hold-up is necessary for calculation of the interfacial area per unit volume and slip velocity. It does not have constant value and can be affected by the operating conditions including rotor speed and dispersed and continuous phases superficial velocities. Thus, the impact of mentioned operating parameters on dispersed phase hold-up has been investigated. Fig. 2 shows the influence of rotor speed on the dispersed phase hold-up. As it is seen, the dispersed phase hold-up increases by increasing the rotor speed. The drops are frequently colliding each other and coalescing at lower rotor speed, therefore the formed larger droplets. For this reason lower rotor speeds have smaller hold-up. By increasing the rotor speed the values of hold-up through the column increase so that the enhancement of the rotor speed reduced the diameter of drop. This phenomenon is because of increasing in the frequency of drop collisions through the internal parts of the extraction column in more turbulent environments.¹⁴ Furthermore, it is also observed that the slope of hold-up verse agitation rate is high for system 3 (n-Butanol–water). This observation could be attributed to low value of interfacial tension. The interfacial energy which is responsible for keeping drop surface is lower in low value of interfacial tension. So, the created turbulent energy with increasing rotor speed is simply overcome to interfacial energy which leads to breaking of drops and creation of smaller drops. With decreasing drops size would decrease rising velocity and increase residence time. Consequently, hold up will increase with higher rate.^14,26 The similar results have been reported for this extraction column by some authors.^15,27

Fig. 2 Effect of rotor speed on the hold-up (V_c = V_d = 6.67 × 10⁻⁴ (m s⁻¹)).

The influence of continuous phase superficial velocity on the hold-up is shown in Fig. 3. It is seen that hold-up increases by increasing the velocity of continuous phase, however, the amount of this variation is not considerable. Also, the effect of dispersed phase flow rate on the column hold-up is illustrated in Fig. 4. It can be observed that an increase in the dispersed phase flow rate leads to an increase in the hold-up. This observation can be resulted in increasing of drops number at constant volume which causes the enhancement of hold-up. The enhancement of dispersed phase flow rate is significant for a system with low value interfacial tension than other two systems. Similar results have been reported in other extraction columns including bubble columns, slurry reactors, airlift loop reactors, fluidized beds and spray extraction columns.^28–30

Fig. 3 Effect of continuous phase flow rate on the hold-up (V_d = 6.67 × 10⁻⁴ (m s⁻¹)).

Fig. 4 Effect of dispersed phase flow rate on the hold-up (V_d = 6.67 × 10⁻⁴ (m s⁻¹)).

Table 3 is provided for comparison of experimental results of hold-up with the results of previous studies. Average Absolute Relative Error (AARE) is used to determine the accuracy of current work. According to the Table 3, it can be resulted that none of the previous correlations are suitable for determination of hold-up in the perforated rotating disc contactor.

Table 3 The AARE values in the predicted values of hold-up obtained by the previous correlation to the experimental data

Investigator	AARE Value
Morís et al. (1997)^31	168%
Kumar & Hartland (1987)^32	71%
Jeffreys et al. (1981)^33	57.98%
Kasatkin et al. (1962)^34	42.21%
Murakami et al. (1978)^35	63.42%

---

Kumar and Hartland developed a novel correlation²¹ for the prediction of dispersed phase hold-up in an RDC column. The expression that used to derive this correlation was formulated by Kumar and Hartland with no mass transfer²¹ which presented in eqn (2):

where g denotes acceleration because of gravity (ms⁻²), ρ_c denotes density of continuous phase (kg m⁻³), σ is the interfacial tension (N m⁻¹), V_d and V_c are dispersed and continuous phases of superficial velocities (ms⁻¹) respectively, Δρ is density difference between phases (kg m⁻³), μ_d and μ_w denote dispersed phase and continuous phase viscosities (Pa s), D_s, D, D_c, h_c are column geometry which mentioned in Table 1 (m), N and Re_R are the rotor speed (rpm) and rotor Reynolds number respectively.

The rotor Reynolds number can be determined as follow equation:

The predicted values of hold-up using eqn (1) with obtained experimental data in this study are shown in Fig. 5. A maximum deviation 45.32% is observed between experimental data and the Kumar and Hartland correlation. The obtained hold-up experimental results are very valuable for the column with sieved discs. This is because the dispersed phase drops in RDC column are larger than PRDC and settled faster. So, the hold-up data which obtained from the Kumar and Hartland correlation are lower than those obtained with sieved discs. In fact, the sieved discs improve the breakup of drops and increase the number of droplets in the extraction column. Therefore, the Kumar and Hartland correlation is not appropriate for prediction of hold-up in PRDC column. Also, the residence time of dispersed phase can be improved by using the perforated discs in the extraction column.³⁶

Fig. 5 Comparison between experimental data and Kumar & Hartland correlation.

3.1.1. Predictive correlation for dispersed phase hold-up. As mentioned above due to different column structure none of correlations in the literature is not suitable for predicating of hold-up in PRDC column. So, one of the main objectives of this study is proposed a correlation to represent the hold-up in a PRDC column. A novel correlation based on operating variables (rotor speed, dispersed and continuous flow rates), column geometry and the system physical properties was developed as follows:

The proposed correlation is validated by using experimental data which reported by Coimbra et al.²⁷ The data of aqueous two phase system of ATPS composed by polyethylene glycol (PEG) and dibasic potassium phosphate (DPP) in a PRDC column with 51 (mm) diameter are investigated.²⁷

The comparison of the experimental data with those calculated by the present model is illustrated in Fig. 6. The average absolute value of the relative error (AARE) of φ between the predicted values using this correlation and the experimental points is 11.10%. According to Fig. 6, there is a very good agreement between experimental results and calculated values by eqn (5).

Fig. 6 Comparison of experimental data with calculated ones from eqn (4).

3.2. Flooding point

The results of flooding rates and hold-up at flooding at four different rotor speeds are shown in Fig. 7 and 8. According to Fig. 7 and 8, allowable dispersed phase velocity decreases with increasing continuous phase velocity. Increasing the continuous phase velocity can be reduced the velocity between the phases. Therefore, the dispersed phase hold-up increases with an increase in continuous phase velocity and consequently the column becomes unstable at lower dispersed phase velocities. From Fig. 7 it can be also concluded that increasing rotor speed is resulted the reduction in the maximum throughput of the extraction column. This is due to a decrease in drop size with increasing rotor speed, which results in an increase in hold-up. Consequently, the critical hold-up is reached at a lower total throughput. Furthermore, total allowable throughput is low for a system with low interfacial tension while it is high for a system with high interfacial tension. It is due to the smaller drops of low interfacial tension system. Fig. 8 also shows that at the higher rotor speed, the hold-up at flooding is greater due to smaller drops formation. Also, the maximum dispersed phase hold-up can be enhanced with increasing the ration of V_df to V_cf. Similar results were obtained for these liquid–liquid systems by Torab-Mostaedi et al.¹⁹

Fig. 7 Experimental variation in V_df with V_cf.

Fig. 8 Effect of V_df/V_cf ratio on the hold-up at flooding (ϕ_df).

The other advantage of flooding measurements is that it can also be used for estimation of the characteristic velocity. Gayler et al.³⁷ and Thornton and Pratt³⁸ proposed an equation and defined a characteristic velocity (V₀) which established a relation between phase flow rates and dispersed phase hold-up. This equation may be written as follows:

At the flood point, the phase flow rates can be derived by differentiating eqn (6) with respect to hold-up. The V_d and V_c are treated as dependent variables. Obtained differential equations are considered equal to zero as follows:

Using of eqn (8) in PRDC column is dependent on the linearity of the characteristic velocity plot. Plotting flood point data in the form of eqn (8) can be obtained a line with a slope of twice the value of V₀. Characteristic velocity plot of flood point data for the butylacetate–water system is shown in Fig. 9. It can be clearly seen that the characteristic velocity concept can be used for PRDC column. It is because linear plot is gained for all investigated liquid–liquid systems. The results of characteristic velocity for three systems are listed in Table 4. According to this table, the characteristic velocity decreases with increasing rotor speed. It also reveals that the enhancement of characteristic velocity with increasing in interfacial tension.

Fig. 9 Characteristic velocity plot of flood point data for the butylacetate–water system.

Table 4 The values of characteristic velocity

Toluene–water		n-Butylacetate–water		n-Butanol–water
N (rpm)	V0 (mm s^−1)	N (rpm)	V0 (mm s^−1)	N (rpm)	V0 (mm s^−1)
300	9.56	240	8.92	180	8.3
360	8.95	300	8.43	240	7.66
420	8.2	360	7.88	300	7.19

---

3.2.1. Predictive correlations for flooding velocities and hold-up at flooding. Developing precise correlations for prediction of flooding velocities and hold-up at flooding is carried out in this study. The experimental data is shown that the maximum throughputs in a PRDC column strongly depend on physical properties of the three liquid–liquid systems and the operating conditions. Several Semi-theoretical correlations have been developed for predicting flooding velocities which are generally derived from hold-up models. Many of these equations are based on the slip velocity method. A wide variety of equations have been proposed for various extraction columns.³⁹ However the following equation was used in many kinds of extractor:

By differentiating the eqn (9) with respect to ϕ_f and considering V_d and V_c as dependent variables at the flood point, dispersed phase and continuous phase flow rates can be calculated by setting the differential equation equal to zero:

Combination of eqn (10) and (11), the limiting value of hold-up at flooding point can be obtained as follows:

Eqn (9) was correlated to the experimental data in this study. The obtained results for the exponent m and the characteristic velocity V₀ from the correlations are presented in Table 5 for three liquid–liquid systems. Based on this table, the values of m are between −5.47 and 1.77 while this range have been reported to be between 0 and 4 for a rotating disc contactor (RDC),³⁹ from 0.3 to 1.5 for a packed column,³⁹ from −3 to 1 for a sieve plate column⁴⁰ and −0.9 to 3.6 for a grasser raining bucket contactor.⁴¹ The difference in m values is probably because of the difference in the extractor structure and the physical properties of the liquid systems which used in different studies. Since PRDC column is known as subset of the RDC extraction column, this method is approximately appropriate for prediction of flooding conditions of n-butylacetate–water system.

Table 5 The values of characteristic velocity and m

Toluene–water			n-Butylacetate–water			n-Butanol–water
N (rpm)	m	V0 (mm s^−1)	N (rpm)	m	V0 (mm s^−1)	N (rpm)	m	V0 (mm s^−1)
300	−4.74	5.86	240	1.68	9.56	180	−1.12	7.08
360	−3.57	6.04	300	1.77	9.19	240	−1.56	5.74
420	−5.74	4.05	360	0.79	6.47	300	−3.82	3.89

---

On the other hands, this method is not appropriate for the other studied liquid–liquid systems including toluene/water and n-butanol/water. This is because the values of m varied between −5.74 and −1.12 under the selected operating conditions. According to eqn (8) and (10), these values would result in unreliable flooding conditions. Also the comparison of the experimental data of dispersed phase flow rate at flooding (V_df) with those calculated by the Kung and Beckmann⁴² model were investigated. The value of AARE of V_df between the predicted values using their correlation and the experimental points is 67.23%. It should be noted that since no information is available in the published literature, empirical correlations are developed in terms of physical properties of liquid–liquid systems and operating variables for prediction of flooding velocities and hold-up at flooding. The experimental data from 75 measurements indicated that the results are found to correlate well by eqn (13).

Fig. 10 shows the comparison of experimental data with those calculated by eqn (13). It can be observed that the experimental results are in good agreement with calculated values obtained by eqn (12). This correlation reproduces the experimental results with an AARE of 3.90%.

Fig. 10 Comparison of experimental values of dispersed phase hold-up at flooding with calculated ones.

Prediction of throughputs when flooding is reached is very important in the design of extraction column. Generally, dispersed phase flow rate at flooding (V_df) is a function of the rotor speed, ration of dispersed phase to continuous phase, and system physical properties. On this basis, the following correlation is derived using the least square method which “Eviews software” version 3.1 is used for this propose:

The comparison between the experimental data and those predicted by using eqn (14) is given in Fig. 11. The value of AARE in the predicted values of dispersed phase flow rate at flooding (V_df) using eqn (14) to the experimental results is 3.55%. This figure indicates that the proposed correlation can estimate velocity of dispersed phase at flooding with high accuracy.

Fig. 11 Comparison of experimental values of velocity of dispersed phase at flooding with calculated ones.

4. Conclusion

This paper presents an experimental study of dispersed phase hold-up, characteristic velocity and flooding behavior in a pilot scale perforated rotating disc contactor. The results showed that the dispersed phase hold-up is significantly affected by the rotor speed and interfacial tension. Maximum hold-up will occur at higher values of rotor speed and low interfacial tension. The results also revealed that an increase in the continuous phase velocity has minimal influence on dispersed phase hold-up while the dispersed phase hold-up increases with an increase in the dispersed phase velocity. The experimental results of hold-up are compared with previous correlations. It is found that the correlations developed for dispersed phase hold-up in RDC columns cannot be used to predict the dispersed phase hold-up in PRDC columns. An empirical expression for dispersed phase hold-up as a function of operating conditions, column geometry and physical properties of the systems is also suggested. Furthermore, the influence of the operating variables and physical properties of liquid systems on flood point characteristics are investigated. According to the obtained results maximum throughput decreases with an increase in rotor speed and flow ratio while it increases with an increase in interfacial tension. The Pratt model is selected for estimation of characteristic velocity because of its simplicity. The results indicated that the characteristic velocity concept can be used for PRDC column but is not applicable for prediction of flood point. Additionally, in the present work, two correlations are derived to predict the flooding velocity and hold-up at flooding in the PRDC column. These equations are shown to describe data satisfactorily. Since there is little experimental data on this type of extractor, these predictive correlations can be used for prediction of maximum capacity of existing PRDC columns and also for final sizing of the column diameter.

Nomenclatures

d32	Sauter mean drop diameter (m)
D	Molecular diffusivity (m^2 s^−1)
Ds	Stator ring diameter (m)
DR	Disc diameter (m)
g	Acceleration due to gravity (m s^−2)
H	Effective height of the column (m)
hc	Compartment height (m)
m	Exponent (−)
N	Rotor speed (s^−1)
Re	Reynolds number (−)
L	Flow ratio (Vd/Vc) (−)
V	Superficial velocity (m s^−1)
V0	Characteristic velocity (m s^−1)
Vs	Slip velocity (m s^−1)
φ	Dispersed phase holdup (−)

Greek letters

ρ	Density (kg m^−3)
Δρ	Density difference between phases (kg m^−3)
κ	Viscosity ratio (ηd/ηc)(−)
μ	Viscosity (Pa s)
σ	Interfacial tension (N m^−1)

Subscripts

c	Continuous phase
d	Dispersed phase
f	Flooding point

Acknowledgements

The authors would like to thank Iran National Science Foundation (INSF) for providing the financial support for this project (Project no. 91003759).

References

1. R. E. Treybal, Liquid Extraction, McGraw-Hill, New York, 2nd edn, 1966.
2. S. Retieb, P. Guiraud, G. Angelov and C. Gourdon, Chem. Eng. Sci., 2007, 62, 4558–4572.
3. R. K. Saini and M. Bose, Energy Procedia, 2014, 54, 796–803.
4. M. Ghadiri, S. N. Ashrafizadeh and M. Taghizadeh, Hydrometallurgy, 2014, 144–145, 151–155.
5. J. Tong and S. Furusaki, J. Chem. Eng. Jpn., 1996, 29, 543–546.
6. J. Tong and S. Furusaki, J. Chem. Eng. Jpn., 1997, 30, 79–85.
7. H. Gross and W. E. Skelton, presented in part at the 3rd World Petroleum Congress, The Hague, the Netherlands, 1951/1/1/, 1951.
8. T. G. S. Laddha and T. E. Degaleesan, Transport Phenomena in Liquid-Liquid Extraction, McGraw Hill, New York, 1976.
9. A. Sakurai, S. Kawamoto, J. F. Abarca and M. Sakakibara, Biochem. Eng. J., 2002, 10, 47–53.
10. Z. Jia-Wen, Z. Shou-Hua, Z. Xiao-Kui, C. Xiao-Xiang, S. Yuan-Fu and A. Vogelpohl, Chem. Eng. Technol., 1991, 14, 167–177.
11. X. Chen, K. Li and Y. Su, Ind. Eng. Chem. Res., 1993, 32, 453–457.
12. B. D. Kadam, J. B. Joshi and R. N. Patil, Chem. Eng. Res. Des., 2009, 87, 756–769.
13. M. T. Cunha, M. J. L. Costa, C. R. C. Calado, L. P. Fonseca, M. R. Aires-Barros and J. M. S. Cabral, J. Biotechnol., 2003, 100, 55–64.
14. A. Hemmati, M. Torab-Mostaedi, M. Shirvani and A. Ghaemi, Chem. Eng. Res. Des., 2015, 96, 54–62.
15. A. L. F. Porto, L. A. Sarubbo, J. L. Lima-Filho, M. R. Aires-Barros, J. M. S. Cabral and E. B. Tambourgi, Bioprocess Eng., 2000, 22, 215–218.
16. M. T. H. Cavalcanti, M. G. Carneiro-da-Cunha, I. V. Brandi, T. S. Porto, A. Converti, J. L. L. Filho, A. L. F. Porto and A. Pessoa, Chemical Engineering and Proccessing, 2008, 47, 1771–1776.
17. Y. Kawase, J. Chem. Technol. Biotechnol., 1990, 48, 247–260.
18. S. Soltanali, Y. Ziaie-Shirkolaee, G. Amoabediny, H. Rashedi, A. Sheikhi and P. Chamanrokh, Chem. Eng. Sci., 2009, 64, 2301–2306.
19. M. Torab-Mostaedi, A. Ghaemi and M. Asadollahzadeh, Chem. Eng. Res. Des., 2011, 89, 2742–2751.
20. R. Berger and K. Walter, Chem. Eng. Sci., 1985, 40, 2175–2184.
21. A. Kumar and S. Hartland, Ind. Eng. Chem. Res., 1995, 34, 3925–3940.
22. A. M. Ismail Al-Rahawi, Chem. Eng. Technol., 2007, 30, 184–192.
23. N. S. Oliveira, D. M. Silva, M. P. C. Gondim and M. B. Mansur, Braz. J. Chem. Eng., 2008, 25, 729–741.
24. T. Misek, R. Berger and J. Schroter, Standard test systems for liquid extraction studies, EFCE Publ., 1985.
25. L. M. Rincón-Rubio, A. Kumar and S. Hartland, Can. J. Chem. Eng., 1993, 71, 844–851.
26. M. G. Samani, J. Safdari, A. H. Asl and M. Torab-Mostaedi, Chem. Eng. Technol., 2014, 37, 1155–1162.
27. J. S. R. Coimbra, F. Mojola and A. J. A. Meirelles, J. Chem. Eng. Jpn., 1998, 31, 277–280.
28. K. R. Jafarabad, T. A. Patil, S. B. Sawant and J. B. Joshi, Chem. Eng. Sci., 1992, 47, 69–73.
29. K. R. Jafarabad, S. B. Sawant, J. B. Joshi and S. K. Sikdar, Chem. Eng. Sci., 1992, 47, 57–68.
30. A. Venâncio and J. A. Teixeira, Bioprocess Eng., 1995, 13, 251–255.
31. M. A. Morís, F. V. Díez and J. Coca, Sep. Purif. Technol., 1997, 11, 79–92.
32. A. Kumar and S. Hartland, Chem. Eng. Commun., 1987, 56, 87–106.
33. G. V. Jeffreys, K. K. M. Al-aswad and C. J. Mumford, Sep. Sci. Technol., 1981, 16, 1217–1245.
34. A. G. Kasatkin, S. Z. Kagan and V. G. Trukhanov, J. Appl. Chem., 1962, 35, 1903–1910.
35. A. Murakami, A. Misonou and K. Inoue, Int. Chem. Eng., 1987, 18, 16–22.
36. C. Pina and A. A. Meirelles, J. Am. Oil Chem. Soc., 2000, 77, 553–559.
37. R. Gayler, V. W. Roberts and H. R. C. Pratt, Chem. Eng. Res. Des., 1953, 31, 57–68.
38. J. D. Thornton and H. R. C. Pratt, Trans. Inst. Chem. Eng., 1953, 31, 289–305.
39. J. C. Godfrey and M. J. Slater, Chem. Eng. Res. Des., 1991, 69, 130–141.
40. A. Hamidi, M. van Berlo, K. C. Luyben and L. A. M. van der Wielen, J. Chem. Technol. Biotechnol., 1999, 74, 244–249.
41. A. D. Giraldo-Zuniga, J. S. R. Coimbra, L. A. Minim and E. E. Garcia Rojas, J. Food Eng., 2006, 72, 302–309.
42. E. Y. Kung and R. B. Beckmann, AIChE J., 1961, 7, 319–324.

---