On the relaxation dynamics in active pharmaceutical ingredients: solid-state ¹H NMR, quasi-elastic neutron scattering and periodic DFT study of acebutolol hydrochloride

Abstract

The molecular dynamics of a cardioselective beta-blocker with intrinsic sympathomimetic activity – acebutolol hydrochloride, was investigated by employing spin-lattice relaxation ¹H nuclear magnetic resonance (NMR) and quasielastic neutron scattering (QENS) experiments along with periodic density functional theory (DFT) computations. The relaxation experiments reveal the presence of four dynamic processes, further assigned to the methyl groups reorientations. The analyzed motions were characterized in terms of their activation barriers and correlation times, while their assignment was supported by theoretical computations. The earlier reported crystallographic structure reveals intriguing features in the large-size unit-cell, defined by eight molecular units. By combining solid-state DFT calculations with the intermolecular interactions analysis (Hirshfeld Surface; Reduced Density Gradient), the nature of the stabilizing crystal forces has been revealed, emphasizing the role of moderate-strength (N–H⋯O; O–H⋯Cl; N–H⋯Cl) and weak (C–H⋯O) hydrogen-bond contacts. The theoretical computations provide clear support for the assignment of particular motions and interpretation of the experimental data as showing a competing influence of both internal-structure and intermolecular factors on their activation barriers. The highest energy barriers were assigned to the acetyl-related methyl rotors, the intermediate ones are due to the isopropyl part, while the most-dynamic methyl groups are assigned to the alkyl chain. Inclusion of crystallographic forces via calculations in periodic boundary conditions was found to be essential for a proper understanding of both the conformational and dynamic properties of the system under interest, as it could not be achieved with molecular modeling. Therefore, the performance of several semi-local exchange–correlation functional approximations was critically examined, revealing a clear tendency in favor of the ‘soft’ and dispersion-corrected schemes for estimation of the rotational barriers in pharmaceutical solids.

---

1. Introduction

Most pharmaceuticals are manufactured, shipped, stored, dispensed and ingested as solids, while it is said that the number of polymorphic forms known for a given compound is proportional to the time and money spent in research on that system.¹ The identification and differentiation of crystal structures are of great importance in the pharmaceutical industry owing to the unique properties that each pharmaceutical polymorph possesses. The crystallization tendency of a given compound is defined both by the dynamic properties of a molecular framework as well as by the presence of specific intermolecular interactions. Both factors are partially driven by temperature, making the understanding of molecular pharmaceutics extremely challenging.

One of the most common systems found in the pharmaceutical industry are the hydrochloride salts, which generally increase the solubility and bioavailability of active pharmaceutical ingredients (APIs). The introduction of hydrochloride significantly affects the intermolecular interactions framework, giving further complication of the phase situation for a given system. Therefore, the progressive exploration of crystallographic forces and molecular dynamics – along with their mutual relation – becomes an important and interesting issue.

Acebutolol (N-{3-acetyl-4-[2-hydroxy-3-(isopropylamino)propoxy]phenyl}butanamide), is a selective β-adrenergic blocking agent, which has been widely used primarily in the treatment of hypertension. It belongs to the second generation blockers and is generally used for treatment of hypertension, angina, arrhythmia and acute myocardial infarction. This group of cardiovascular pharmaceuticals is relatively selective for β₁-adrenoceptors. However, the relative selectivity can be lost at higher doses of drugs. Acebutolol along with other beta adrenergic blocking agents are derivatives of aryloxy-isopropyl-aminopropanol. A common feature in the chemical structure is that there is at least one aromatic ring attached to a side alkyl chain possessing a hydroxyl and amine group. Each of the beta-blockers has one or more chiral centers in its structure. For this reason, acebutolol exist as S(−) and R(+)-enantiomers but most of the β-blocking activity resides in the S(−)-enantiomer.² Acebutolol like a majority of other β-blockers is used in clinical practice as a racemate. It has been well documented that the enantiomers of β-adrenergic blocking agents differ significantly not only in their pharmacodynamic activity but also in their pharmacokinetic profiles. The two enantiomers of a specific racemate interact quite differently with biological systems and a major part of human metabolism is stereoselective.

Acebutolol is a well-known drug, being, however, sparely investigated at the molecular level. The commercially available racemate form, with the trade names Monitan Prent, Rhotral, Sectral et al., is the hydrochloride salt. Acebutolol·HCl is a white – or slightly off-white – crystalline solid, being freely soluble in water and less soluble in ethanol.

The hydrochloride was proved by thermal analysis, infrared spectroscopy, and X-ray powder diffraction to exist in three crystalline forms (form I, II, and III) and, additionally, in an amorphous form.³ The equilibrium phase is denoted as Form I, while the remaining polymorphs (Form II and Form III) can be described as metastable pseudopolymorphs, undergoing spontaneous transformations. The equilibrium form is unsolvated, while the metastable pseudopolymorphs include a noticeable water content. The relaxation of each metastable phase is then accompanied by water release.³

The crystallographic structure of form I has been previously reported by Carpy et al.⁴ and will be discussed in details further on. Since the crystal structure is defined by the presence of multiple prominent short contacts, including the H⋯Cl attractions, it was further explored by Hildebrand et al.⁵ using ³⁵Cl solid-state NMR spectroscopy. The quoted papers are the only reports focused on the structural properties of acebutolol hydrochloride, where, however the intermolecular interactions were not studied in details.

The main motivation of the paper is, hence, to shed more light on the relation of intermolecular interactions with molecular dynamics of acebutolol hydrochloride. For this purpose we have employed the state-of-the-art experiments, namely the second-moment of NMR line and spin–lattice relaxation ¹H NMR over a wide temperature range along with the Quasi-Elastic Neutron Scattering (QENS) on the highly-intense neutron source (ILL, Grenoble). The interpretation of the experimental results was supported by modern solid-state density functional theory (DFT) calculations. The wealth of present intermolecular interactions, along with the competing influence of both structural and environmental factors on the relaxation dynamics, were thoroughly analyzed. Since there is very little information about the calculations of reorientation barriers in large molecular crystals, the performance of several available semi-local exchange–correlation DFT functionals has been critically examined.

2. Experimental and computational details

Sample

Acebutolol hydrochloride was purchased from Gedeon Richter Polska Sp. zoo. (Grodzisk Mazowiecki, Poland).

Powder X-ray diffraction measurements were carried out with an Empyrean (PANalytical) diffractometer, using Cu Kα radiation (1.54 Å), reflection-transmission spinner (sample stage) and PIXcel 3D detector, operating in the Bragg–Brentano geometry. The 2 Theta scans were recorded at room temperature (300 K) with the angles ranging from 5 to 60 (°2 Theta) with a step size of 0.013 (°2 Theta), using the continuous scan mode.

Differential scanning calorimetry (DSC) experiment was performed with a DSC 8000 apparatus (Perkin-Elmer, Norwalk, USA) at the heating and cooling rate of 10.0 K min⁻¹ in the temperature range of 170–450 K.

¹H nuclear magnetic resonance experiments

A powder sample of acebutolol hydrochloride was placed in a glass ampoule of 8 mm inner diameter, then degassed and sealed off under vacuum.

The second moment of the ¹H NMR line was obtained from the continuous wave 28 MHz spectrometer (El-lab Tel-atomic). The measurements were done in a temperature range of 100–198 K, with a 10 K step. The temperature of the sample was stabilized using a gas-flow cryostat with liquid nitrogen as cooling agent and monitored by a Pt resistor with an accuracy of 0.1 degrees.

The spin–lattice relaxation time (T₁) were studied on ¹H NMR pulse spectrometers working at resonant frequencies of 58.9 MHz and 25.0 MHz (El-Lab Tel-atomic) using the saturation-recovery method over the following temperature programs, namely: from 100 K up to room temperature using the 58.9 MHz setup and from 30 K up to room temperature for the 25.0 MHz setup, respectively. The spin–lattice relaxation time in the rotating frame T_1ρ with the magnetic field B₁ = 18 G were measured using the pulse spectrometer working at frequency 58.9 MHz (El-Lab Tel-atomic) by spin-locking methods over the temperature range 200–300 K.

Both spectrometers were equipped with cryostats: nitrogen with an accuracy of 0.1 K (58.9 MHz) and helium–nitrogen with an accuracy of 0.01 K (25.0 MHz). Temperature stabilization was set on the level of 1 degree and 0.1 degrees, respectively.

Quasi-elastic neutron scattering

The sample for QENS measurements was prepared by placing 0.450 g of acebutolol hydrochloride in an aluminium flat container (dimension of 30.0 mm × 40.0 mm) with a thickness of 0.25 mm (in order to get a transmission of about 0.9). The empty cell and a vanadium sample with a thickness of 1.0 mm were also measured to obtain the instrument background and resolution, respectively.

The experiment was performed on the time-of-flight IN5 spectrometer (Institute Laue-Langevin, Grenoble, France) working with a neutron wavelength of λ = 6 Å and an energy resolution of 35 μeV (FWHM). This setup allows to examine the Q range of 0.3–1.6 Å⁻¹. The angle between the incident neutron beam and the sample was fixed to 135°. The measurements were done at 300 K, where the temperature was stabilized by a helium–nitrogen cryostat with an accuracy of 0.01 degrees.

The raw experimental data were treated with LAMP software (Institute Laue-Langevin, Grenoble, France) including: the subtraction of background from an empty cell, the correction with the detector efficiency, the normalization to the vanadium spectrum and the correction for the absorption. Additionally, the detectors where Bragg peaks influenced the registered spectra were removed from further analysis.

Computational details

In order to analyze the structural properties of acebutolol hydrochloride, the solid-state formulation of density functional theory (DFT) was employed. The periodic DFT calculations were performed using two different codes, namely DMOL³ v. 7.0 (ref. 6 and 7) and CASTEP v. 8.0.⁸ Despite the large system size, defined by eight molecules per conventional unit cell, the computations were performed with high numerical precision, which is needed to properly describe the potential energy surface (PES). Multiple generalized gradient approximations (GGA) of the exchange–correlation (XC) functional were used as discussed further on.

The DMOL³ calculations were performed in the full-electronic approach, using the double numerical radial function basis set (DNP), which is comparable to the Gaussian double zeta plus polarization set of functions (6-31G**), being, however, generally recognized as more accurate than the Pople's basis set formulation. The calculations were performed for both, crystal and isolated molecule models. Electronic energy calculations and geometry optimization were performed as to reach the following convergence criteria in variation of the total energy, maximum gradient, maximum displacement, and SCF iterations equal to: 5 × 10⁻⁷ Ha, 5.0 × 10⁻⁴ Ha Å⁻¹, 5 × 10⁻⁴ Å and 1 × 10⁻⁸ Ha per atom, respectively.

Alternatively, the CASTEP calculations were employed by using more diffused plane-wave/pseudopotential methodology. The norm-conserving pseudopotentials (NCPP), constructed according to Rappe–Rabe–Kaxiras–Joannopoulus (RRKJ)^9,10 scheme, were used along with the 1050 eV (77 Ry) plane-wave kinetic energy cutoff. The convergence criteria in variation of the total energy, maximum force, maximum displacement, and SCF iterations were defined as: 5 × 10⁻⁷ eV per atom, 2.5 × 10⁻³ eV Å⁻¹, 5 × 10⁻⁴ Å and 1 × 10⁻⁹ eV per atom, respectively.

In both modeling schemes, the computations were performed with the constrained-cell optimization, using delocalized internal coordinates, where the Monkhorst–Pack grid was kept to maintain the k-spacing of 0.07 Å⁻¹. Occasionally, the full-cell optimization was done with CASTEP using dispersion-corrected DFT under atmospheric pressure conditions.

In order to support the interpretation of the NMR/QENS results, the methyl reorientation profiles were calculated through the rigid scan of their dihedral angles, that is, without subsequent relaxation of remaining internal coordinates. The nature of the activation barriers was underpinned through the crystal environment analysis. For this purpose, the Hirshfeld surface^11–16 and the Non Covalent Interactions (NCI)^17–19 analyses were employed.

3. Results and discussion

Sample characteristics

The structural formula of acebutolol hydrochloride (a) is given in Fig. 1a. There are four methyl groups in the molecular unit, denoted as 1, 2, 3 and 4, respectively. The room-temperature crystal structure of the equilibrium Form I is visualized in Fig. 1b, according to the data reported by Carpy et al.⁴

Fig. 1 The structural formula of acebutolol hydrochloride (a) along with the adopted methyl group notation (1; 2; 3; 4). The crystal packing of Form I in the frame of the conventional unit cell (b) (298 K) according to Carpy et al.⁴ against the molecular conformation of the asymmetric unit (298 K) (c).

The system was found to crystallize in the monoclinic C₂/c space group, defined by the following cell parameters: a = 27.552(3) Å; b = 4.995(1) Å; c = 29.122(4) Å; α = γ = 90.0°; β = 99.55(1)°. There are eight molecules equivalent by symmetry in the conventional unit cell. Hence, the single molecular unit defines the asymmetric part of the crystal structure. The dispersion-corrected PBE-D2 (ref. 20–22) cell-optimization (referring to 0 K) provides the volume shrinking down to 332.44 ų w.r.t. the room-temperature data, defined by the following cell-parameters: a = 27.004 Å; b = 4.862 Å; c = 27.745 Å; α = γ = 90.0°; β = 96.394°. One can hence expect that there are no conformational changes accompanying the temperature evolution, and that the crystal undergoes only a slight thermal cell expansion.

The crystal structure of the studied sample (Form I) was confirmed by the powder X-ray diffraction and the differential scanning calorimetry (DSC) analysis. Both results stay in line with the PXRD and differential thermal analysis (DTA) data, reported by Awata et al.³

The experimental PXRD patterns are shown in Fig. 2a against the diffraction patterns simulated, both, from the structure reported by Carpy et al.⁴ and from the representative CASTEP/PBE/1050 eV data. One can note that both theoretical patterns are undistinguishable, staying in excellent agreement with the experimental spectrum, with only minor differences reflected in the intensity relations at the lowest angles (note the range of 5–10°).

Fig. 2 The powder X-ray diffraction profiles of acebutolol hydrochloride (a) the experimental spectrum collected for the studied sample (PXRD 298 K) is presented against the theoretical patterns simulated, both, from the single-crystal structure of Form I solved at 298 K (Carpy et al.⁴) and from the representative DFT structure, optimized at the 298 K cell constants (CASTEP PBE). (b) The results of the differential scanning calorimetry (DSC) analysis of the sample under interest.

The differential scanning calorimetry (DSC) analysis provides the second proof of the presence of the unsolvated Form I. The DSC thermogram reveals only a single endothermic peak found at 419.2 K, that may be assigned to the melting process of form I (see Fig. 2b). The calculated enthalpy of the transition equals ca. 110.0 J g⁻¹. One may note that the melted Form I undergoes amorphization at around 325 K, which, however, cannot be clearly observed due to the relatively slow cooling rate required (10 K min⁻¹).

Solid-state ¹H NMR and QENS study

In order to explore the molecular motions, two spectroscopic methods were applied, namely the proton nuclear magnetic resonance (¹H NMR) and quasielastic neutron scattering (QENS) measurements. These two complementary spectroscopy methods allow to perform a detailed analysis of molecular reorientations in a wide temperature range.

The measurements of the second moment of the NMR line and spin–lattice relaxation time T₁ are shown in Fig. 3a and b, respectively. The value of M₂ decreases from 17 G² to 14 G² in the temperature range of 100–140 K, while at higher temperature conditions it evolves monotonically (within the experimental error) from 14.6 G² (140 K) to 13.6 G² (300 K).

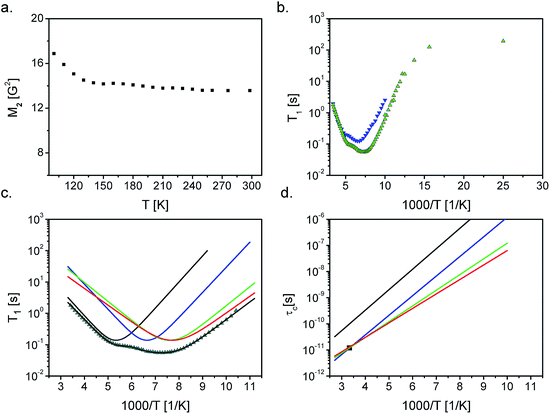Fig. 3 (a) Second moment of NMR line versus temperature, (b) relaxation time versus inverse temperature for acebutolol hydrochloride at 25 MHz and 58.9 MHz (c), relaxation time versus inverse temperature for acebutolol hydrochloride and the best fit to the experimental points with eqn (1) assuming four activation processes (solid lines) at 25 MHz (d) the correlation time obtained from NMR measurements (solid lines) and QENS (■). The errors are the size of experimental points.

Only two minima of T₁ are observed at the 25 MHz spectrometer at the temperatures T = 178.5 K and 137 K (1000/T = 5.6 and 1000/T = 7.3), respectively, and their values are equal to 0.13 s and 0.08 s. At the 58.9 MHz setup, the minima are shifted toward higher temperatures (Fig. 3b). To be sure that there is no additional T₁ minimum at higher temperature, we performed additionally measurements of T_1ρ in the temperature range of 300–200 K. No additional minimum was found, which confirms that the observed two minima of T₁ relaxation are the only ones in a wide temperature range.

The temperature independence of the measured second moment at higher temperatures is the result of an average of the second moment by reorientation/motions which start below 100 K (i.e., below the lowest temperature available in our experiment). Taking into account the shape of the acebutolol cation it is reasonable to assume the occurrence of methyl groups' reorientation.

On the basis of the crystallographic data and using van Vleck formula²³ the second moment M₂ corresponding to the rigid lattice was calculated. Its value equals 23.7 G² and is much higher than the experimental value observed at the lowest temperature available. This confirms that the measured M₂ is averaged by molecular reorientations and that its frequency is greater than that corresponding to the line width for the rigid structure. As mentioned above, the most probable ‘candidates’ for reorientation are methyl groups. Therefore Monte Carlo simulations of second moment NMR lines were performed using the computer program described in ref. 24. The simulations were done for 27 unit cells with the assumption that four methyl groups can reorient. This kind of reorientation reduces the value of the second moment to 14.5 G², which is in a very good agreement with the experimental value. Monotonic decreases of the second moment observed experimentally are connected with the iso-propyl group oscillations and ethyl group oscillations (within ±20°), which, according to the calculations reduce M₂ approximately of 1 G².

On the basis of measurements of M₂ we could conclude that all methyl groups reorient, but this experiment did not allow to tell more about their activation energy and/or correlation time. Such information was provided by measurements of the relaxation time. The well-known BPP formula was fitted to the temperature dependence of T₁:²⁵

where τ_c = τ₀ exp(E_a/RT) is the correlation time (the Arrhenius relation), τ₀ is a constant, E_a is the activation energy, R is the gas constant, C is a relaxation constant, and ω₀ is the resonance frequency.

As already mentioned in a wide temperature range there are only two minima of T₁. However, acebutolol contains four methyl groups and therefore four relaxation processes (with the same C constant) were fitted (Fig. 3c). They describe very well the experimental points and the parameters obtained for the reorientation are summarized in Table 1. The experimentally estimated activation barriers (using the 25 MHz setup) are 14.9 ± 0.2, 14.4 ± 0.2, 11.7 ± 0.3 and 10.6 ± 0.1 kJ mol⁻¹, respectively, while for 58.9 MHz spectrometer are slightly higher. It should be underlined that the attempts to analyze the data with use of only 1, 2 or 3 relaxation processes provide a significantly worse fit. These values are comparable with those obtained for the reorientation of methyl groups in other compounds.^26–32

Table 1 The activation parameters obtained from fitting four processes (corresponding to four methyl groups reorientation) to T₁ relaxation–spin time measured at 25 MHz

	1st process	2nd process	3rd process	4th process
τ0 [s]	(2.5 ± 0.4) × 10^−13	(0.35 ± 0.1) × 10^−13	(1.04 ± 0.2) × 10^−13	(1.81 ± 0.6) × 10^−13
Ea [kJ mol^−1]	14.9 ± 0.2	14.4 ± 0.2	11.7 ± 0.3	10.6 ± 0.1
C [s^−2]	(7.90 ± 0.04) × 10^8	(7.90 ± 0.04) × 10^8	(7.90 ± 0.04) × 10^8	(7.90 ± 0.04) × 10^8

---

The activation energies of each of the methyl groups considered are different. A deeper minimum reflects the reorientation of three methyl groups, while – a shallower one (at higher temperatures) reflects only one methyl group. Fig. 3d shows the dependence of the correlation times as a function of inverse temperature (calculated based on the data from Table 1 with an assumption of the Arrhenius relationship). The correlation times for three methyl groups (deeper minimum) converge at room temperature, while the correlation time of the fourth group is longer, which means that its reorientation is slower.

To understand better the discussed phenomena, a quasielastic neutron scattering measurement was performed on IN5 spectrometer at room temperature.

A representative spectrum (Q = 1.0 A⁻¹) of acebutolol hydrochloride is shown in Fig. 4. In all cases the spectra were fitted with the following expression (convoluted with the resolution function R(Q,ω)):

S(Q,ω) = A₀(Q)δ(ω) + (1 − A₀(Q))L(ω) + B(Q,ω), (2)

where: A₀(Q) is called the elastic incoherent structure factor, L(ω) is a Lorentz function of half-width at half-maximum Γ and B(Q,ω) describes the linear background. The spectra were fitted using the DAVE package³³ which enables to perform a numerical convolution with the instrumental resolution function R(Q,ω) determined from the vanadium measurement.

Fig. 4 Experimental (■) elastic incoherent structure factor (EISF_meas). Solid lines are the theoretical line obtained from eqn (4) assuming reorientation of 1, 2, 3, 4 methyl groups. Inset – normalized QENS spectra for acebutolol hydrochloride Q = 1.0 A⁻¹ (points). The solid line (red) shows the fitted spectra, the dotted (blue) line corresponds to the quasielastic contribution, the dashed (black) is the resolution function, the dashed-dotted (black) line is the background.

A quasi-elastic broadening is clearly visible and was well fitted using only one Lorentzian function. As we have four methyl groups that may reorient with different characteristic times we also performed additional fits assuming more than one (2, 3 or 4) Lorentzian function. However the fit with a single Lorentzian line reproduces very well the quasielastic broadening observed and we could not improve the fitting using the additional set of functions. The width of the Lorentzian line (within the uncertainty limit) does not depend on Q, which gives a strong support to the model of jumps between three minima.

Two important parameters were extracted from the fitting: the correlation time (inversely proportional to the half-width of the Lorentz function Γ) and A₀(Q), which provides information about the geometry of motion and is directly equal to the elastic incoherent structure factor (EISF). It means that this phenomenological fit permits us to determine the EISF in a model independent way. Assuming jumps of methyl groups between three equidistance sites on a circle of radius r, the corresponding elastic incoherent structure factor can be written as:³⁴

While all atoms in the sample contribute to the EISF, the contribution from the hydrogen atoms represents more than 90% of the total scattering, so the contribution from other atoms (nitrogen, carbon, oxygen, chloride) can be neglected. Furthermore in the crystal structure studied here we can assume that only the motion of the methyl groups can take place within the time scale given by the finite resolution of the spectrometer, which in the case of our experiment in IN5 is of the order of several hundred ps. Therefore the measured elastic incoherent structure factor (EISF) can be written as

where the parameter c represents the ratio of immobile hydrogen atoms over the total number of protons, c = (28 − 3n)/28, 28 is the total number of hydrogen atoms in the acetobutolol molecule and n is the number of methyl groups (between 1 and 4) that appear as mobile in the experimental time scale. The measured EISF obtained from the fit of the QENS spectra using eqn (2) is displayed in Fig. 4, together with the theoretical lines corresponding to eqn (4) for n = 1, 2, 3, and 4. It appears clear that the experimental points are best described by the model involving reorientations of three methyl groups. The half-width Γ obtained from the fitting of the QENS spectra is related to the correlation time τ_c by Γ = 3ħ/(2τ_c).³⁴ The correlation time established from QENS experiment is displayed on Fig. 3d, which is in a very good agreement with NMR data.

NMR measurement reveled that four methyl groups are dynamically inequivalent and characterised by different activation energies. At the lower temperatures their correlation times are quite different. With increasing temperature the correlations times approach each other and at room temperature correlation times of three of the four methyl groups are equal. This conclusion is also supported by QENS measurements. To understand better the dynamically non-equivalency of the methyl groups we perform a detailed analysis of the crystal structure and intermolecular interactions together using solid-state DFT calculations.

The intermolecular interactions

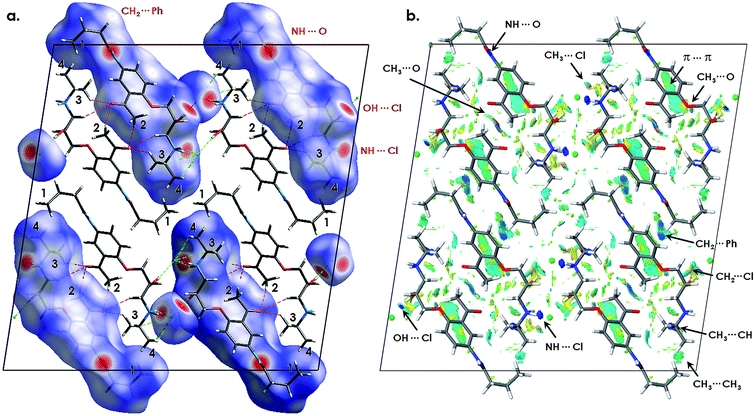
The structural formula of acebutolol hydrochloride given in Fig. 1a shows that there are four methyl groups in the molecular unit, denoted as 1, 2, 3 and 4, respectively. From the molecular point of view, one can expect that the acetyl-related methyl group (no. 2) should be distinct from, both, alkyl (no. 1) and isopropyl (no. 3 and 4) ones, which might be generally treated as nearly equivalent. Nevertheless, the presence of specific interactions and influence of the crystal environment may affect the methyl groups dynamics to a great extent. Indeed, the spin–lattice NMR relaxation experiments indicate the presence of four reorientation processes with the energy barriers of 14.9 ± 0.2, 14.4 ± 0.2, 11.7 ± 0.3 and 10.6 ± 0.1 kJ mol⁻¹, respectively. In order to assign the dynamically non-equivalent species it is hence necessary to analyze the crystal structure in details.

In order to underpin the nature of the forces stabilizing the structure, the intermolecular interactions analysis has been employed via the Hirshfeld surface and the reduced density gradient (RDG; NCI – non covalent interactions) analyses, based on the pro-molecular densities and the experimental crystal structure with the hydrogen positions further optimized with CASTEP at the standard PBE level of theory.^20,21 The results are projected in Fig. 5.

Fig. 5 Hirshfeld surface analysis of the intermolecular interactions in acebutolol hydrochloride plotted in the unit-cell projection toward the crystallographic b-axis (a). The Cl⋯H (<3.00 Å) and O⋯H (<2.75 Å) close contacts are denoted as green and red dashed lines, respectively. Isosurface delivered by the reduced density gradient (RDG) analysis (intermolecular; density cutoff = 0.30; color range of +0.0175 (attractive)/−0.0175 (repulsive)) (b). Significantly attracting forces are colored in blue, whereas the repulsive interactions are shown in red. Weak van der Waals forces are marked in green and yellow, following their repulsive character.

By analyzing the figure, one can note that the crystal packing significantly affects the molecular conformation, resulting in the gauche twisting of the terminal chains. One can assume that the crystal stabilization through the intermolecular forces tends to be favorable over the possibly straightened and planar acebutolol's geometry. It is hence clear, that the crystal packing is expected to significantly affect the methyl groups' dynamics.

Fig. 5a represents the Hirshfeld surfaces plotted on a half of the molecular units. A Hirshfeld surface represents the interaction of the electron density of selected molecule with that of the surrounding crystal structure. The surface is defined at the point where contribution to the calculated electron density from the object and the surrounding is equal. The property projected here is the normalized contact distance (d_norm) from the surface to the nearest external atom (white – distance (d) equals the van der Waals (vdW) distance; blue – d exceeds the vdW distance; red – d is less than the vdW distance).

The crystal packing leads to the formation of long-range, moderate-strength N–H⋯O hydrogen bonds through the H–N–C=O fragments, which link the parallelly oriented acebutolol molecules toward the crystallographical axis-b. By analyzing Fig. 5a one can see intense red spots around the oxygen and nitrogen atoms expressing the O–H⋯N hydrogen bonds. The crystallization in the form of hydrochloride results in the occurrence of prominent O–H⋯Cl and N–H⋯Cl bonds, which are also clearly manifested on the surface. By analyzing the close contacts, one can find that methyl groups no. 2 and 4 are expected to have higher rotational barriers due to interactions with the electron donating heavy atoms, while the methyl groups no. 1 and 3 are expected to be less affected as being only under the influence of weak vdW forces. Such assumption stays in line with the above mentioned experimental results.

Nevertheless, the weak, more delocalized interactions are less pronounced on the Hirshfeld surface. In order to get further insight into their nature, a second visual aid has been applied. The NCI analysis¹⁷ refers to the electron density and its derivatives. In general, it originates from the analysis of the reduced density gradient (RDG) at the low densities. Differentiation between the non-covalent interactions is based on the analysis of the sign of the second density Hessian eigenvalue times the density, where the results can be presented in the form of isosurfaces. The RDG analysis reported here is derived from the pro-molecular densities.

Fig. 5b expresses the presence of above quoted hydrogen bonds (see NH⋯O; NH⋯Cl; and OH⋯Cl in Fig. 2b) through the localized, deep blue areas. What is more, it provides a direct differentiation between the weak forces. The analysis reveals the CH₃⋯Cl (no. 4) interactions as localized, light blue spots. Although the interactions are not clearly manifested in the present figures, one can expect a significant influence of the electron-rich chloride which may acts as a multi hydrogen bonding acceptor. It is further supported by the analysis of the chloride atom distance, found at ca. 2.9 Å, staying in line with the literature reports of CH⋯Cl interactions.³⁵

As indicated, the molecules are parallelly N–H⋯O bonded in the b-axis direction. The NCI analysis reveals that the parallel orientation is further stabilized by prominent, displaced stacking interactions (π⋯π) between the phenyl rings, which manifest themselves as delocalized cyan areas. One can also note that methyl groups no. 2 are in close contact with the alkoxy-bridge oxygen from the neighboring molecules (CH₃⋯O). Furthermore, one can note the antiparallel acebutolol packing in the c-axis direction. Such arrangement is stabilized by mutual CH₃⋯O bonding of the neighboring acetyl groups, which may further raise the activation barriers of the methyl groups no. 2. Hence, one can expect that among the present rotors, the quoted CH₃ groups would be the most hindered ones, that is having the greatest activation barriers. The antiparallel acebutolol arrangement is further stabilized by the CH₂⋯π (see CH₂⋯Ph in Fig. 5b) interactions. Such forces also manifest in the Hirshfeld surface as small, bright, red spots.

The remaining CH₃ groups (no. 1 and 3) are not considerably influenced by the heavy atoms. The methyl group no. 3 is separated from the acetyl oxygen for about ∼2.6 Å (where, however, the acetyl groups are already mutually bonded as quoted above). It is interesting to note, that the NCI analysis reveals prominent H⋯H interactions between the neighboring isopropyl moieties, where the CH₃ (no. 3) groups are in close contact (∼2.1 Å) with the neighboring C–H fragments (CH₃⋯CH). Such attractive interactions seems to be prominent, as according to the X-ray analysis, the related C–CH₃ bond length is about ∼0.03 Å longer than for the remaining rotors. Hence, one may expect that the related barrier height should be the smallest one.

Finally, the methyl groups no. 1 in the gauche alkyl chains are in close contact with the isopropyl ones (no. 4), as being separated from each other for ca. ∼2.5 Å (see CH₃⋯CH₃ in Fig. 5b). There is no specific interactions affecting the quoted rotors, while, however, they span into the alkyl-crowded crystal area and the local strain (and the repulsion interactions) may raise the related barriers.

In summary, the crystal environment analysis suggests that the higher energy barriers, estimated as 14.9 ± 0.2 and 14.4 ± 0.2 kJ mol⁻¹, can be assigned to the CH₃ groups no. 2 and 4, respectively. The second pair of rotors, with the barriers of 11.7 ± 0.3 and 10.6 ± 0.1 kJ mol⁻¹, can be attributed to the methyl groups denoted as 1 and 3.

Theoretical calculations of the activation barriers

In fact, a proper assignment of the reorientation barriers derived from relaxation experiments is usually impossible without employing theoretical calculations. However, most of the literature reports are typically supported by the isolated-molecule models, which can lead to a serious misinterpretation of the experimental results, since the crystal environment is hard to be ignored in most cases. There is very little literature data about calculations of CH₃ barriers in molecular crystals, and practically there is no benchmark studies in this area. On the other hand, the prediction of the reorientation barriers in solid-state is definitely not a trivial task as one needs to face the balance of accuracy in, both, the potential energy surface (PES) definition and the description of external forces. In order to shed more light on this problem, we have employed periodic DFT calculations, which, however, deserve further comments.

Conceptually, the potential energy calculated at each step can be broken down into intra- and intermolecular contributions, which correspond to regions of high and low electron density, respectively. The latter contributions can be related to the Coulombic and vdW contributions. Unfortunately, probably, the most serious shortcoming of DFT is associated with the dispersion forces description, which are generally related to the long-range electron correlation effects, being notoriously absent from local and semi-local density functionals. Moreover, the dispersion forces stem from dynamic correlation, which cannot be defined properly through modification of the exchange energy description, hence it also concerns more non-local hybrid XC functionals. The accuracy that can be reached with a pure GGA approach is strongly limited due to a rather simple mathematical form, depending on the electron density ρ and its derivative ∇ρ. Nevertheless, because of the size of large molecular assemblies as well as present limitations of solid-state codes, one is usually limited to the use of semi-local, pure DFT approach. There is however a chance, that due to a crowding in the solid-state, the short-range interactions can be partially taken into account, since the failure asymptotic behaviour between non-polar systems in semi-local DFT occurs mainly at larger distances. The calculations reported here, should be, hence, rather interpreted with a warning, as a qualitative estimation, since one cannot treat the GGA DFT as an accurate tool in calculations of the intermolecular interactions energy.

In the present work we have examined several GGA schemes available. The most conventional GGA approximations are known as BP;^36,37 the stand-alone PW91 ³⁸ or its simplified PBE revision.^20,21 The conventional GGA schemes were examined against several alternative formulations with more empirical motivation. The BLYP scheme, combining the Becke's (B88) exchange term³⁶ with the Lee–Yang–Parr correlation,^39,40 was used along with the later proposed BOP approach, combining an alternative correlation functional of Tsuneda and Hirao^41,42 and sharing the same exchange contribution. Both functionals are known for an adaptation of the so-called orbital-dependent correlation energy formula of Colle and Salvetti. Alternatively, a strongly-parametrized GGA of Hamprecht, Cohen, Tozer and Handy (HCTH)⁴³ in its final form was used, where 15 parameters were refined over the set of 407 systems (HCTH/407).⁴⁴

Most GGA approximations can be compared in terms of an analytic function known as the exchange energy enhancement factor (F_x(s)) that, in principle, is a measure of its non-locality. The exchange energy shows a simple trend in the interaction of two separate species, that is, it increases with the distance, up to some critical point, where it starts decreasing. At large separations, it continues to decrease. Generally, there is a binding at short separations, whereas at large distances, there is mainly repulsion. In the ‘Functional ZOO’, the conventional PBE scheme is considered as the standard one in calculations of solids as obeying many of the exact theoretical conditions and devoid any fitting parameters. By treating PBE as a reference, we have examined its so-called ‘soft’ and ‘hard’ formulations, namely PBE for solids (PBEsol),⁴⁵ and revised PBE (rPBE).⁴⁶ The former one has the exchange enhancement factor that increases more slowly with the reduced density gradients than PBE. In the opposite, in ‘hard’ rPBE the enhancement factor rises more rapidly, making the functional more non-local. While the former one generally provides a better description of the cell-constants in molecular crystals, the latter one is superior in the internal-coordinates definition.

Finally, two ad hoc approaches for correcting the vdW deficiency of standard PBE were introduced, namely the Grimme's D2 corrections²² and Tkatchenko–Scheffler approach.⁴⁷ The quoted methods introduce slightly different semi-empirical dispersion correcting damping functions for each pair of atoms, separated by a given distance, along with different dispersion C₆^ij coefficients. In the Grimme method, the C₆^ij coefficients depend only on the chemical species, while in the TS scheme, the coefficients are calculated on-the-fly by factoring the effect of the chemical environment.

The theoretically estimated barrier heights are collected in Fig. 6. The given histograms represent the results of GGA calculations for each methyl group, delivered with the help of both, DMOL³ and CASTEP codes. The moderate quality atom-centered full-electronic DMOL³ calculations allows one to check the solid-state and methodological influence as referring, both, to periodic (298 K cell volume) and isolated molecule approaches, with the use of a rich selection of available GGA functionals. In addition, the CASTEP calculations represent an alternative approach, which can be considered as a more precise due to a relatively more accurate basis set definition, which essentially covers the whole unit-cell space.

Fig. 6 The activation barriers for methyl group (no. 1–4) reorientation in acebutolol hydrochloride as predicted by density functional theory (DFT) in generalized gradient approximation (GGA). The DMOL³ results refer to the isolated molecule equilibrium geometries (patterned bars) and constrained-cell (298 K) optimized crystal structures (single-color bars). The CASTEP results refer to the constrained-cell optimized crystal structures at the 298 K cell constants (one color bars). The activation barriers per molecular unit are given in kJ mol⁻¹.

One should also keep on mind that the static calculations refer to 0 K, hence, do not take into account any temperature effects, which can affect the rotational barriers through the abundance of the coupled vibrational states. Hence, the theoretically estimated barriers are expected to be slightly higher by definition. Moreover, the experimentally determined values are derived from the points collected over a wide temperature range, where, the cell-volume and intermolecular distance – and thereby the interactions strength – evolve, resulting in mean values. Hence, one can only juxtapose the averaged values with a single-configuration data, which can leads to further discrepancies.

The analysis of Fig. 6 suggests that more accurate CASTEP results deliver lower activation barriers. If treating the dispersion-corrected periodic calculations as possibly most-reliable, one can see progressive deviations toward more non-local approximations (rPBE; HCTH).

By analyzing the DMOL³ results one can note a difference between the isolated molecule model and the periodic results for each methyl group rotation. For the CH₃ groups no. 1, 3 and 4, each XC functional in the vacuo model delivers similar barrier heights. In contrary, in the case of methyl group no. 2 one can note a strong functional dependence. Such an effect can be clearly understood by analysis of the equilibrium conformation of the acebutolol·HCl adduct. The results for each functional differ in the orientation of the acetyl group (O=C–CH₃), while there is a significant internal CH₃⋯O (alkoxy) interaction. The crystallographic analysis reveals the acetyl group to be twisted from the phenyl ring plane for 13° (the Ψ(O=C–C=C) = 167°), while the isolated molecule calculations provide the twisting varying from 11 (PBE-TS) to 34° (BOP; HCTH), which directly reflects the anomalous values of the predicted barrier heights. In contrary, each functional in the periodic approach (both DMOL³ and CASTEP) properly predicts the acetyl orientation as giving only slight variation of the results (∼11–13°). The resulting barriers only vary from ∼17–18 kJ mol⁻¹ in most cases. Hence, the periodic calculations suggest that the acetyl group orientation is strongly stabilized in the solid-state. As mentioned earlier in the discussion of crystal structure, the neighboring, antiparallel acetyl groups form dimeric connections. Nevertheless, one could expect that higher temperature may induce large oxygen displacements. In order to further explore such an effect, the 2D potential energy surface (PES) scans were performed and illustrated in Fig. 7.

Fig. 7 Two-dimensional total-energy dependence (standard PBE level) in function of reorientation of the methyl group no. 2 from its optimized position (ΔΨ(CH₃) = 0°) against the acetyl group twisting from its equilibrium orientation (ΔΨ(O=C–C=C) = 0°). (a) refers to the isolated-molecule model (DMOL³/PBE/DNP) while (b) comes from the periodic model (CASTEP/PBE/1050 eV/NCPP).

By analyzing Fig. 7a, presenting dependence of the methyl reorientation barrier on the acetyl group twisting, one can see that the molecule is flexible. Hence, even large acetyl group twisting from its equilibrium (15°) does not give strong raise of the total energy (only ca. 2.02 kJ mol⁻¹), hence it could be easily populated by the temperature. In such a way, the internal CH₃⋯O (alkoxy) distance would significantly grows, leading to very significant lowering of the CH₃ activation barriers. In contrary, Fig. 7b, presents the same dependence for the crystal phase. One can see, that the above mentioned strong stabilization through the CH⋯O interactions makes the system very rigid. Both methyl reorientation and acetyl twisting are strongly hindered and cannot be easily populated by temperature. It hence makes the belief that the CH₃ groups no. 2 should be characterized by the highest activation barriers as observed experimentally at 14.9 ± 0.2 kJ mol⁻¹.

The calculations clearly confirm, that there is another CH₃ group with a high activation barrier, which can be assigned to the second process: 14.4 ± 0.2 kJ mol⁻¹ CH₃ no. 4. If referring to the CASTEP calculations, there is a clear tendency for lowering of the height as going from ‘hard’ GGA (rPBE) to ‘soft’ PBEsol (which gives here the results comparable to PBE-D2). The intermolecular interaction analysis have linked the energy barrier with the long-range CH⋯Cl interactions. One can also expect that such interactions would depend on the cell volume, and hence the temperature. Therein, one can expect that the experimentally found activation barriers should be slightly lower than for the strongly hindered CH₃ no. 2.

Two methyl groups no. 1 and 3 are described by the experimental activation barriers of 11.7 ± 0.3 and 10.6 ± 0.1 kJ mol⁻¹, respectively. Taking the groups no. 2 and 4 as the reference, one can estimate that the theoretically predicted values should of the order of ∼12–13 kJ mol⁻¹. While there is no big functional dependence in the case of CH₃ no. 3, the DMOL³ results seem to provide a significant overbinding for the CH₃ no. 1. As discussed earlier on, there is a prominent molecular crowding affecting the conformation of terminal chains. Such an effect can raise the activation barriers for methyl groups no. 1. Nevertheless, as stated in the structural section, these rotors are in fact only in contact with the methyl groups no. 4. The activation barriers are hence too large if referring to more non-local functionals. PBE-D2 data, recognized as the most reliable here, cannot in fact differentiate these two rotors. It seems that – as for all the remaining methyl groups in acebutolol hydrochloride – the most reasonable results were delivered by PBEsol.

4. Conclusions

In summary, we may conclude that the ¹H NMR and QENS experiments supported by periodic DFT calculations provide a clear insight into the molecular dynamics of acebutolol hydrochloride, which could be successfully understood by combination of experimental and theoretical analysis. The molecular dynamics was clearly attributed to the methyl groups' reorientation and have been described, both, qualitatively and quantitatively.

The qualitative analysis in terms of the crystal structure and intermolecular interactions analysis, clarify the presence of four inequivalent CH₃ rotors, being the markers of different-strength crystal environment. The Hirshfeld Surface and Reduced Density Gradient analysis, emphasize the role of moderate-strength (N–H⋯O; O–H⋯Cl; N–H⋯Cl) and weak (C–H⋯O) hydrogen-bond contacts in the crystal phase stabilization.

The quantitative analysis, delivered by the experiments and DFT calculations, provides the reorientation barriers and correlation times. The theoretical computations provide a clear support for assignment of particular motions and interpretation of the experimental data as showing the competing influence of both internal-structure and intermolecular factors on their activation barriers. The highest energy barriers were assigned to the acetyl-related methyl rotors, the intermediate ones are due to the isopropyl part, while the most-dynamic methyl groups are assigned to the alkyl chain.

The theoretical estimation of the activation barriers reach the accuracy of ∼2 kJ mol⁻¹ for selected functionals, which tends to be a reasonable value as neglecting the temperature influence. Nevertheless, we should also conclude that none of the tested approaches can be used without a chemical intuition or as a predictive tool in the calculations of CH₃ reorientation barriers. Although, some trends are clearly present if comparing different GGA approximations, none of the pure-DFT approaches can provide satisfying results. Among the tested schemes, the most reasonable results were delivered by ‘soft’ PBEsol approach, while more non-local functionals were found to be highly inaccurate. Nevertheless, its relative success should be rather linked with the well-known overbinding tendency or lucky-compensation of errors rather than its any theoretical justification. The most promising approach should be referred to the semiempirically vdW corrected DFT, that is, PBE-D2 and PBE-TS schemes. While PBE-TS is generally recognized as more advanced approach, in the present case it tends to deliver some further anomalies. Although being less specific in parametrization, the PBE-D2 scheme seems to be superior in the present case.

In perspective, the application of more advanced vdW corrections schemes for DFT solid-state calculations may be promising and definitely call for further benchmark analysis. Probably the most efficient and promising way of dealing with large molecular crystals would be oriented toward modern ad hoc corrections as for example represented by the many-body Tkatchenko–Scheffler scheme,^48,49 Grimme's D3 approach,⁵⁰ Silvestrelli's maximally localized Wannier functions (MLWFs) approach,^51,52 or exchange-hole dipole moment (XDM) theory.^53,54 Nevertheless, none of the actually available solid-state codes provides a simultaneous access to the most of the above mentioned methodologies, limiting their applicability.

Acknowledgements

The work has been partially financed by the National Science Centre of Poland, Grant No. 2012/05/B/ST3/03176 and by the operating program POKL 4.1.1. Financial support from the National Centre for Research and Development under research grant “Nanomaterials and their application to biomedicine”, contract number PBS1/A9/13/2012, is also gratefully acknowledged. This research was supported in part by PL-Grid Infrastructure (Grant ID: phd2014, phd2013). The calculations with use of DMOL3 were performed within Polish National Accelrys License (Mars Supercomputer, CYFRONET, AGH, Cracow). The financial support of Polish Government Plenipotentiary for JINR in Dubna, Russia (Grant No. 44/27-01-2015/7/1121/5) is also gratefully acknowledged.

References

1. W. C. McCrone, in Physics and Chemistry of the Organic Solid State, ed. D. Fox, M. M. Labes and A. Weissberger, Interscience Publishers, London, 1965, vol. 2, pp. 725–767.
2. M. Piquette-Miller, R. T. Foster, C. T. Kappagoda and F. Jamali, Pharmacokinetics of acebutolol enantiomers in humans, J. Pharm. Sci., 1991, 80, 313–316.
3. N. Awata, K. Yamamoto, H. Nakagawa, I. Sugimoto, H. Sakata, H. Sato and Y. Zashi, Polymorphism of acebutolol hydrochloride, J. Pharm. Soc. Jpn., 1979, 99, 141–145.
4. A. Carpy, M. Gadret, D. Hickel and J. M. Leger, Chlorhydrate D'Acebutolol (Hydroxy-2 Isopropylamino-3 Propoxy)-2 Butyrylamino-5 Acetophenone Chlorhydrate, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1979, 35, 185.
5. M. Hildebrand, H. Hamaed, A. M. Namespetra, J. M. Donohue, R. Fu, I. Hung, Z. Gan and R. W. Schurko, 35Cl solid-state NMR of HCl salts of active pharmaceutical ingredients: structural prediction, spectral fingerprinting and polymorph recognition, CrystEngComm, 2014, 16, 7334–7356.
6. B. Delley, An All-Electron Numerical Method for Solving the Local Density Functional for Polyatomic Molecules, J. Chem. Phys., 1990, 92, 508–517.
7. B. Delley, From Molecules to Solids with the DMol3 Approach, J. Chem. Phys., 2000, 113, 7756–7764.
8. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, First Principles Methods Using CASTEP, Z. Kristallogr., 2005, 220, 567–570.
9. A. M. Rappe, K. M. Rabe, E. Kaxiras and J. D. Joannopoulos, Optimized Pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 1227–1230.
10. A. M. Rappe, K. M. Rabe, E. Kaxiras and J. D. Joannopoulos, Optimized Pseudopotentials – Erratum, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 13175.
11. J. J. McKinnon, A. S. Mitchell and M. A. Spackman, Hirshfeld Surfaces: A New Tool for Visualising and Exploring Molecular Crystals, Chem.–Eur. J., 1998, 4, 2136–2141.
12. M. A. Spackman and J. J. McKinnon, Fingerprinting Intermolecular Interactions in Molecular Crystals, CrystEngComm, 2002, 4, 378–392.
13. J. J. McKinnon, M. A. Spackman and A. S. Mitchell, Novel Tools for Visualizing and Exploring Intermolecular Interactions in Molecular Crystals, Acta Crystallogr., Sect. B: Struct. Sci., 2004, 60, 627–668.
14. J. J. McKinnon, D. Jayatilaka and M. A. Spackman, Towards Quantitative Analysis of Intermolecular Interactions with Hirshfeld Surfaces, Chem. Commun., 2007, 3814–3816.
15. M. A. Spackman and D. Jayatilaka, Hirshfeld Surface Analysis, CrystEngComm, 2009, 11, 19–32.
16. S. K. Wolff, D. J. Grimwood, J. J. McKinnon, M. J. Turner, D. Jayatilaka and M. A. Spackman, Crystal Explorer, Version 3.1, University of Western Australia, 2012.
17. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, Revealing Noncovalent Interactions, J. Am. Chem. Soc., 2010, 132, 6498–6506.
18. J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J. P. Piquemal, D. N. Beratan and W. Yang, NCIPLOT: a Program for Plotting Non-Covalent Interaction Regions, J. Appl. Crystallogr., 2010, 43, 1250–1260.
19. R. M. Hanson, Jmol - A Paradigm Shift in Crystallographic Visualization, J. Appl. Crystallogr., 2010, 43, 1250–1260.
20. J. P. Perdew, K. Burke and Y. Wang, Generalized Gradient Approximation for the Exchange-Correlation Hole of a Many-Electron System, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533–16539.
21. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
22. S. Grimme, Semiempirical GGA-Type Density Functional Constructed With a Long-Range Dispersion Correction, J. Comput. Chem., 2006, 27, 1787–1799.
23. J. H. Van Vleck, The dipolar broadening of magnetic resonance lines in crystals, Phys. Rev., 1948, 74, 1168–1183.
24. R. Goc, Computer calculation of the Van Vleck second moment for materials with internal rotation of spin groups, Comput. Phys. Commun., 2004, 162, 102–112.
25. C. P. Slichter, Principles of Magnetic Resonance, Springer-Verlag, Berlin, 3rd enlarged and updated edn, 1996.
26. J. Wasicki, D. P. Kozlenko, S. E. Pankov, P. Bilski, A. Pajzderska, B. C. Hancock, A. Medek, W. Nawrocik and B. N. Savenko, NMR search for polymorphic phase transformations in chlorpropamide form-A at high pressures, J. Pharm. Sci., 2009, 98, 1426–1437.
27. J. Mielcarek, D. M. Nowak, A. Pajzderska, B. Peplinska and J. Wasicki, A hybrid method for estimation of molecular dynamics of diazepam-density functional theory combined with NMR and FT-IR spectroscopy, Int. J. Pharm., 2012, 404, 19–26.
28. A. Pajzderska, D. M. Chudoba, J. Mielcarek and J. Wąsicki, Calorimetric, FTIR and 1H NMR measurements in combination with DFT calculations for monitoring solid-state changes of dynamics of sibutramine hydrochloride, J. Pharm. Sci., 2012, 101, 3799–3810.
29. A. Pajzderska, K. Drużbicki, M. A. Gonzalez, J. Jenczyk, B. Peplinska, M. Jarek, J. Mielcarek and J. Wasicki, Experimental and Solid-State Computational Study of Structural and Dynamic Properties in the Equilibrium Form of Temazepam, J. Phys. Chem. B, 2014, 118, 6670–6679.
30. C. Smuda, G. Gemmecker and T. Unruh, Quasielastic and inelastic neutron scattering study of methyl group rotation in solid and liquid pentafluoroanisole and pentafluorotoluene, J. Chem. Phys., 2008, 128, 194502–194511.
31. M. Prager, H. Grimm, S. F. Parker, R. Lechner, A. Desmedt, S. McGrady and E. Koglin, Methyl group rotation in trimethylaluminium, J. Phys.: Condens. Matter, 2002, 14, 1833–1845.
32. E. R. Andrew, M. Kempka, J. M. Radomski and E. Szcześniak, Molecular dynamics in solid anhydrous β-estradiol studied by 1H NMR, Solid State Nucl. Magn. Reson., 1999, 14, 91–94.
33. R. T. Azuah, L. R. Kneller, Y. Qiu, P. L. W. Tregenna-Piggott, C. M. Brown, J. R. D. Copley and R. M. Dimeo, DAVE: A comprehensive software suite for the reduction, visualization, and analysis of low energy neutron spectroscopic data, J. Res. Natl. Inst. Stand. Technol., 2009, 114, 341–358.
34. M. Bee, Quasielastic Neutron Scattering, Hilger, Bristol, 1988.
35. Y.-R. Zhong, M.-L. Cao, H.-J. Mo and B.-H. Ye, Syntheses and Crystal Structures of Metal Complexes With 2,2′-Biimidazole-like Ligand and Chloride: Investigation of X-H···Cl (X = N, O, and C) Hydrogen Bonding and Cl-π (Imidazolyl) Interactions, Cryst. Growth Des., 2008, 8, 2282–2290.
36. A. D. Becke, Hartree–Fock Exchange Energy of an Inhomogeneous Electron Gas, Int. J. Quantum Chem., 1983, 23, 1915–1922.
37. J. P. Perdew, Density-Functional Approximation for the Correlation Energy of the Inhomogeneous Electron Gas, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
38. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Atoms, Molecules, Solids, and Surfaces: Applications of the Generalized Gradient Approximation for Exchange and Correlation, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687.
39. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti Correlation-Energy Formula Into a Functional of the Electron Density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
40. B. Miehlich, A. Savin, H. Stoll and H. Press, Results Obtained with the Correlation Energy Density Functionals of Becke and Lee, Yang and Parr, Chem. Phys. Lett., 1989, 157, 200–206.
41. T. Tsuneda and K. Hirao, A New Spin-Polarized Colle-Salvetti-Type Correlation Energy Functional, Chem. Phys. Lett., 1997, 268, 510–520.
42. T. Tsuneda, T. Suzumura and K. Hirao, A New One-Parameter Progressive Colle–Salvetti-Type Correlation Functional, J. Chem. Phys., 1999, 110, 10664–10678.
43. F. A. Hamprecht, A. J. Cohen, D. J. Tozer and N. C. Handy, Development and Assessment of New Exchange–Correlation Functionals, J. Chem. Phys., 1998, 109, 6264–6271.
44. A. D. Boese and N. C. Handy, A New Parametrization of Exchange-Correlation Generalized Gradient Approximation Functionals, J. Chem. Phys., 2001, 114, 5497–5503.
45. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces, Phys. Rev. Lett., 2008, 100, 136406–136410.
46. B. Hammer, L. B. Hansen and J. K. Nørskov, Improved Adsorption Energetics Within Density-Functional Theory Using Revised Perdew-Burke-Ernzerhof Functionals, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421.
47. A. Tkatchenko and M. Scheffler, Accurate Molecular Van Der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data, Phys. Rev. Lett., 2009, 102, 073005–073009.
48. A. Tkatchenko, R. A. DiStasio Jr, R. Car and M. Scheffler, Accurate and Efficient Method for Many-Body van der Waals Interactions, Phys. Rev. Lett., 2012, 108, 236402.
49. A. Ambrosetti, A. M. Reilly, R. A. DiStasio Jr and A. Tkatchenko, Long-Range Correlation Energy Calculated From Coupled Atomic Response Functions, J. Chem. Phys., 2014, 140, 18A508.
50. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
51. P. L. Silvestrelli, Van der Waals Interactions in DFT Made Easy by Wannier Functions, Phys. Rev. Lett., 2008, 100, 053002.
52. P. L. Silvestrelli, van der Waals Interactions in Density Functional Theory Using Wannier Functions, J. Phys. Chem. A, 2009, 113, 5224–5234.
53. A. D. Becke and E. R. Johnson, Exchange-Hole Dipole Moment and the Dispersion Interaction Revisited, J. Chem. Phys., 2007, 127, 154108.
54. A. D. Becke and E. R. Johnson, A Unified Density-Functional Treatment of Dynamical, Nondynamical and Dispersion Correlations, J. Chem. Phys., 2007, 127, 124108.

---