Multi-scale study of hydrodynamics in an interconnected fluidized bed for the chemical looping combustion process
Abstract
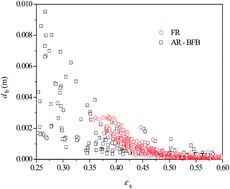
During the chemical looping combustion (CLC) process, the gas–solid hydrodynamic behaviors have a direct influence on the stability of the reactor system and the combustion efficiency of the fuel. To gain a better insight into the CLC system, a multi-scale computational fluid dynamic (CFD) simulation is implemented with an integrated drag model considering the impact of bubbles and clusters under the framework of the two-fluid model. A cluster-structure dependent drag model and a bubble-structure dependent drag model are employed to describe the meso-scale effects caused by clusters and bubbles. By comparisons of the gas pressure profile, the model prediction agrees well with experimental results. The distributions of local structural parameters including velocities in the bubble and emulsion, bubble fraction and local velocities in clusters are analyzed.

 Please wait while we load your content...
Please wait while we load your content...