Pyrolysis versus hydrolysis behavior during steam decomposition of polyesters using ¹⁸O-labeled steam

Abstract

Steam decomposition, a method employed for the depolymerization of polyesters, does not require solvents, catalysts, or high pressure. During steam decomposition, the fission of the ester group occurs by hydrolysis, whereas the ester group is cleaved without the action of water during pyrolysis, affording reduced monomer yields. Hence, elucidating the contribution of hydrolysis and pyrolysis to depolymerization in a steam atmosphere, as well as the effect of polyester structure on selectivity, will improve the accuracy of kinetic analyses and maximize monomer yields. In this study, the selectivities for pyrolysis and hydrolysis during the steam decomposition of polyethylene terephthalate (PET), polybutylene terephthalate (PBT), and polyethylene 2,6-naphthalate (PEN) were quantified using ¹⁸O-labeled steam at different steam concentrations and decomposition temperatures. The decomposition temperature strongly affected the hydrolysis selectivity for PET and PBT, whereas that for PEN was hardly affected. The selectivity for polyester hydrolysis increased with increasing steam concentration for both PET and PEN, with the exception of PBT. These results revealed that the selectivities for both pyrolysis and hydrolysis were significantly affected by the structure of the polyester. In addition, the thermogravimetric kinetic analysis of steam decomposition was consistent with the results of the ¹⁸O-labeling experiments.

---

1. Introduction

The ester bonds in polyester chains are well known to be cleaved by pyrolysis and hydrolysis. Both reactions enable the depolymerization of high-molecular-weight polyesters into monomers; thus, are commonly applied for the feedstock recycling of waste polyesters such as polyethylene terephthalate (PET),^1–19 polybutylene terephthalate (PBT),^8,20–22 and polyethylene 2,6-naphthalate (PEN).^13,14,22,23

On the other hand, pyrolysis is an attractive method because it only requires heat. Detailed mechanisms for the pyrolysis of aromatic polyesters have been reported previously. In this process, cyclic oligomers such as dimers, trimers, and tetramers are initially formed by intramolecular exchange.^24–28 These oligomers are further decomposed by β-hydrogen transfer to the carbonyl carbon via six-membered ring intermediates,^29,30 resulting in carboxylic acids such as terephthalic acid (TPA) and 2,6-naphthalene dicarboxylic acid (NDC), which can be used as feedstock for polyester synthesis. However, typically low recovery rates are obtained for these carboxylic acids, as vinyl esters that are simultaneously produced cannot be further pyrolyzed to carboxylic acids.

On the other hand, hydrolysis proceeds by the nucleophilic attack of the carbonyl carbon by water. Hence, hydrolysis enables the recovery of carboxylic acids in high yield. However, subcritical and supercritical conditions,^2,13,19,23 as well as the addition of acid or base catalysts,^4,6,7 are often required because under neutral conditions, the hydrolysis of polyesters is very slow,^31–33 caused by their low water solubility. In addition, if polyester wastes contain additives such as metals or glass fillers, any solvent that is present must be regenerated after prolonged use as the additives accumulate in the medium. Finally, mixed polymers must be separated before the process. Hence, suitable plastics are limited for hydrolysis.

Herein, we examine the steam decomposition of polyesters, which exploits the advantages of both pyrolysis and hydrolysis. In this process, decomposition is conducted under steam at the pyrolysis temperature, allowing for the hydrolysis of polyesters at a speed more rapid as compared to that without catalysis at atmospheric pressure. On the other hand, inorganic additives can be separated as solids by the volatilization of organics.³⁴ Furthermore, other plastics, which typically must be separated before solvolysis, can be simultaneously decomposed into oil and gas compounds.³⁵ Hence, steam decomposition is a key technology for overcoming the obstacles of both pyrolysis and hydrolysis.

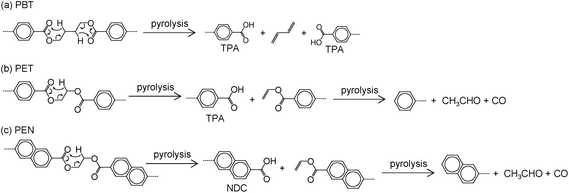
Hydrolysis and pyrolysis simultaneously occur during the steam decomposition of polyesters because it is conducted at high temperatures; the latter has a negative impact on the yield and selectivity of monomers. However, to the best of our knowledge, very little is known about the mechanism and kinetics of polyester decomposition under steam,³ although pyrolysis and hydrolysis have been widely reported. Thus, the manner in which pyrolysis affects hydrolysis still remains unclear, and vice versa. Hence, we developed a novel approach for quantifying the selectivities for pyrolysis and hydrolysis during the steam decomposition of PET using ¹⁸O-labeled steam (Scheme 1).³⁶ Selectivity is calculated from the ratio of labeled and unlabeled TPA determined by gas chromatography-mass spectroscopy (GC-MS).

Scheme 1 Identification of (a) pyrolysis and (b) hydrolysis products in the ¹⁸O-labeled steam decomposition of PET.³⁶

In this study, the pyrolysis-versus-hydrolysis behavior of PET, PBT, and PEN during steam decomposition was investigated using our approach. Understanding this behavior is useful for predicting the decomposition mechanism and optimizing product yields. In addition, by the comparison of the three polyesters, the influence of the polymer structure on the pyrolysis and hydrolysis selectivities for each transformation was clarified during steam decomposition. For this purpose, the influence of steam concentration and decomposition temperature on the pyrolysis and hydrolysis selectivities in PET, PBT, and PEN was investigated using ¹⁸O-labeled steam. In addition, kinetic analyses of the steam decomposition of these polyesters were conducted by model-fitting techniques using a thermogravimetric analyzer. The results obtained from the ¹⁸O-labeling tests and kinetic analyses were compared for consistency. Our previously published letter briefly describes some of the results for PET.³⁶ However, all experiments for PET were repeated and updated for an accurate comparison with the results for PBT and PEN under the same conditions.

2. Experimental

2.1 Materials

A PET bottle (M_w = 22 300), PBT pellets (M_w = 28 000, Sigma-Aldrich Co., LLC.), and PEN pellets (M_w = 48 900, Teijin Ltd) were ground to a particle size below 250 μm. The compositions of these materials, as revealed by elemental analyses, were very close to their theoretical values. Thermogravimetric analysis (room temperature to 500 °C at 5 °C min⁻¹) of the materials was conducted for determining the onset temperature (temperature for 5% weight loss) of pyrolysis, affording values of 378, 352, and 399 °C for PET, PBT, and PEN, respectively. Steam decomposition experiments were conducted near these temperatures.

¹⁸O-Labeled water (H₂¹⁸O) with a purity of >98% (SKChem Co., Ltd) was diluted to 10 wt% with ion-exchanged water and used for labeling experiments. 1-Methyl-3-nitro-1-nitrosoguanidine (Tokyo Chemical Industry Co., Ltd), methyl tert-butyl ether, and a 5 M NaOH solution (Kanto Chemical Co., Inc.) were purchased for the preparation of diazomethane. Tetrahydrofuran (THF) was obtained from Kanto Chemical Co.

2.2 ¹⁸O-labeled steam decomposition of polyesters

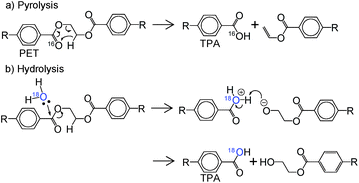
Experiments were conducted using a tube reactor, as shown in Fig. 1(a), which consist of a decomposition chamber, a steam generator, and product traps. Before the experiments, samples (200 mg) were placed into a hole-punched sample holder suspended by a stainless steel wire outside of the heating zone at the top of the reactor until the required conditions were achieved. The reactor temperature was set between 320 and 440 °C at the required He flow rate. When constant temperature was achieved, ¹⁸O-labeled steam was added to the gas flow in a ratio to produce steam concentrations of 0, 25, 50, or 75 vol% (total flow rate of He and steam: 300 mL min⁻¹). Once constant conditions were achieved, the sample holder was lowered into the heating zone, where it was held until decomposition was complete (maximum of 8 h, caused by the water capacity of the steam generator). After the experiment was terminated, the reactor walls and traps were washed with THF to dissolve decomposition products, and THF was then completely evaporated. The recovered products were washed with ethanol and dried for furnishing pure TPA or NDC. The yields of TPA and NDC were calculated using eqn (1).

Fig. 1 Tube reactor and TGA both equipped with steam generators (1) flow meter, (2) digital thermometer, (3) thermocouples, (4) 10 wt% H₂¹⁸O labeled water, (5) boiling stone, (6) coil heater, (7) sample holder, (8) tube reactor, (9) electric furnaces, (10) ice trap, (11) liquid nitrogen trap, (12) gas bag.

We confirmed that neither TPA nor NDC decomposed under the reaction conditions. In addition, the exchange of the ¹⁸O-labeled hydroxyl group of TPA and steam, and vice versa, was not observed when unlabeled TPA was exposed to ¹⁸O-labeled steam, because TPA underwent immediate sublimation and was carried beyond the heating zone. In contrast, a maximum of 5% exchange between the ¹⁸O-labeled hydroxyl group of NDC and steam, and vice versa, was observed under the conditions, caused by its higher sublimation temperature.

2.3 Analytical methods

The proportions of ¹⁸O-labeled and -unlabeled TPA and NDC were determined by GC-MS. To reduce the sublimation temperature of TPA and NDC, they were esterified to dimethyl terephthalate (DMT) and dimethyl-2,6-naphthalene dicarboxylate (DMN) using diazomethane, which prevented the substitution of ¹⁸O-labeled oxygen. Diazomethane was synthesized by dripping a 5 M NaOH solution (5 mL) into a solution of 1-methyl-3-nitro-1-nitrosoguanidine (1.0 g) in ion-exchanged water (2.5 mL) under N₂. The gaseous diazomethane generated was dissolved in ice-cooled methyl tert-butyl ether (10 mL).

Both DMT and DMN were analyzed by GC-MS (Agilent Technologies; GC: HP6890; column: InertCap 5 MS/Sil; MS: HP5973, program: 50 °C (5 min) → 5 °C min⁻¹ → 320 °C). The hydrolysis of the polyesters resulted in three mass peaks for each dimethyl dicarboxylate produced, corresponding to molecules containing two ¹⁶O isotopes, one ¹⁶O and one ¹⁸O isotope, or two ¹⁸O isotopes: m/z = 194, 196, and 198 for DMT and m/z = 244, 246, and 248 for DMN. For instance, Fig. 2 shows the MS spectra of the products obtained from pyrolysis and decomposition at a steam concentration of 50 vol%. The intensities of the peaks at m/z = 196, 198, 246, and 248 significantly increased in the presence of ¹⁸O-labeled steam.

Fig. 2 MS spectra obtained from pyrolysis at a steam concentration of 50 vol% during the decomposition of (a) PET, (b) PBT, and (c) PEN.

The selectivities for pyrolysis and hydrolysis to the steam decomposition of PET and PBT were calculated using eqn (2) and (4) and those of PEN were determined from eqn (3) and (4):

here, S_H represents the hydrolysis selectivity [%], and S_P represents the pyrolysis selectivity [%]. The terms of I_m/z refer to the intensities of peaks caused by H₂¹⁸O steam decomposition (m/z = 196, 198, 246, 248) [−], or to pyrolysis (m/z = 196, 198, 246, 248) [−]. The term Y refers to the yield of TPA or NDC. The intensities of the naturally occurring compounds at m/z = 196, 198, 246, and 248 (I_B196, I_B198, I_B246, and I_B248) as background obtained from pyrolysis were subtracted from I₁₉₆, I₁₉₈, I₂₄₆, and I₂₄₈, respectively. In addition, the intensities of m/z = 196 and 246 were divided by two, as one of the two carboxyl groups was hydrolyzed. The hydrolysis ratio was multiplied by 10 as 10 wt% H₂¹⁸O was used. Finally, S_H values were standardized by the TPA or NDC yield.

2.4 TGA measurements and kinetic analysis

A thermogravimetric analyzer (TGA: TG/DTA 6200, Seiko Instruments) equipped with a steam generator was used for the kinetic analysis of steam decomposition (Fig. 1(b)). The samples were hydrolyzed under a gas flow of 300 mL min⁻¹ with steam concentrations of 0, 25, 50, and 75 vol% under He. The steam flow was controlled by adjusting the furnace temperature of the steam generator. Isothermal conditions were maintained between 350 and 400 °C for avoiding consideration of the compensation effect, which is well known to complicate the results obtained by non-isothermal methods.^37,38 The measurements were controlled by Muse 4.1 software (Seiko Instruments), and microsoft excel was used for all calculations.

The reacted conversion α_r (α_r = (W₀ − W)/(W₀ − W_f), where W₀ [mg]: initial mass, W [mg]: actual mass, W_f [mg]: final mass) for each run was fitted to an integrated form of kinetic reaction models g(α_r) taken from the solid-state reaction models^37,39 summarized in Table 2 in our previous study.⁴⁰ The theoretical α_r vs. g(α_r)/g(0.5) master plots of each model were compared with the experimental α_r vs. t/t_0.5 plot (reduced-time master plot), where t [min] is the actual time, and t_0.5 [min] is a time of α_r = 0.5, resulting in some possible models.^41,42

The possible models selected by the reduced-time master plot method were further evaluated by the linearity r_Model of t vs. g(α) plot based on the integrated form of eqn (5) under all conditions, where α is the conversion (α = 1 − W/W₀). The reverse regression coefficient R_Model [−] was calculated using eqn (6) for improving visualization, and then the three most probable reaction models were selected. The apparent reaction rate constant k_app [min⁻¹] was determined from the slope of the t vs. g(α) plot, and the apparent activation energy E_app [kJ mol⁻¹] and pre-exponential factor k₀ [min⁻¹] were determined from the Arrhenius plot.

g(α) = k_appt (5)

R_Model = −log(1 − r²_Model) (6)

In this study, for focusing on the chain scission stage, kinetic analysis was conducted in the range 0.2 ≤ α ≤ 0.6 for avoiding an unstable temperature range (α < 0.2) and carbonization range (α > 0.6) as much as possible.

3. Results and discussion

3.1 Influence of decomposition temperature on selectivity

The influence of temperature on the steam decomposition of PET, PBT, and PEN was investigated up to 440 °C at a steam concentration of 75 vol% containing ¹⁸O-labeled steam (Fig. 3). We did not conduct experiments below 340, 320, and 380 °C for PET, PBT, and PEN, respectively, as complete sample decomposition within 8 h was not ensured as these temperatures. The hydrolysis selectivity during PET decomposition was 46% at 340 °C with a TPA yield of 75%. With increasing temperature, both the hydrolysis selectivity and TPA yield decreased because of the influence of competitive pyrolysis, resulting in only 11% hydrolysis selectivity with a TPA yield of 42% at 440 °C. The dramatic decrease in the TPA yield at 440 °C was attributed to the significant deposition of coke on the sample holder wall. An unquantifiable amount of char was observed below 440 °C.

Fig. 3 Selectivities of pyrolysis and hydrolysis as well as monomer yields obtained from (a) PET, (b) PBT, and (c) PEN at different temperatures at a steam concentration of 75 vol%.

On the other hand, hydrolysis selectivity during the degradation of PBT was significantly influenced by the reaction temperature: it decreased from 81% at 320 °C to 27% at 440 °C. PBT exhibited hydrolysis selectivity higher than that of PET. The higher selectivity is possibly attributed to the easier access of steam to the ester bonds of PBT because its chain is more flexible than those of PEN and PET. The TPA yield was not influenced by the reaction temperature, and an average yield of 70% was obtained. In addition, char deposition was not observed over the investigated temperature range. The lack of influence of the decomposition temperature on the TPA yield is attributed to the production of TPA via β-scission.²⁷ Because of its longer diol unit, PBT can undergo β-scission at both ends of the diol to release TPA (Scheme 2(a)). During the scission of the ester bond, ethylene-glycol-based polyesters with short diol units form vinyl esters, which prevent the same reaction at the opposite side. The degradation of the vinyl ester results in the simultaneous decarboxylation of the carboxylic acid (Scheme 2(b) and (c)).

Scheme 2 Mechanisms of pyrolysis for (a) PBT, (b) PET, and (c) PEN.

The selectivities for pyrolysis and hydrolysis during the decomposition of PEN were not affected by the reaction temperature, although the NDC yield decreased from 81% at 380 °C to 61% at 440 °C. Char was deposited on the reactor walls under all conditions, suggesting that PEN easily forms char by pyrolysis, caused by its rigid structure. In addition, the vapor pressure of NDC was significantly lower than that of TPA. Hence, NDC might stay on the PEN surface longer than TPA on PET and PBT, resulting in the formation of char caused by the suppression of the access of steam to PEN. However, the constant selectivities indicate that hydrolysis was also accelerated with increasing temperature. Hence, the rigid PEN structure possibly becomes more flexible with increasing temperature, enhancing access to the ester bonds by the steam.

3.2 Influence of steam concentration on selectivity

PET, PBT, and PEN were decomposed at 400 °C at steam concentrations of 0, 25, 50, and 75 vol% containing ¹⁸O-labeled steam. Fig. 4 summarizes the selectivities for pyrolysis and hydrolysis and the monomer yields. The TPA yield was 50% during the decomposition of PET under pyrolysis conditions. The hydrolysis selectivity was only 7%, with a slight increase in the TPA yield to 56% at a steam concentration of 25 vol%. Both the hydrolysis selectivity and TPA yield increased proportionally with steam concentration, resulting in a maximum selectivity of 23% with a TPA yield of 78% at a steam concentration of 75 vol%.

Fig. 4 Selectivities of pyrolysis and hydrolysis as well as monomer yield obtained from (a) PET, (b) PBT, and (c) PEN at different steam concentrations at 400 °C.

Neither the selectivities nor the TPA yield was influenced by the steam concentration during the steam decomposition of PBT, resulting in an average of 36% for the hydrolysis selectivity for a TPA yield of 69%. The influence of the steam concentration on hydrolysis selectivity might be hindered by the strong contribution by pyrolysis at 400 °C; among these materials, PBT exhibited the lowest pyrolysis onset temperature (352 °C). However, the flexible polymer chain afforded hydrolysis selectivity higher than that observed for PET. The constant TPA yields are due to β-scission from both ends of the long diol unit, as explained in the previous section.

In the case of PEN, only 38% NDC was recovered under pyrolysis conditions, caused by the significant production of char on the sample holder wall. Both the NDC yield and hydrolysis selectivity increased to 19%, with an NDC yield of 62% at a steam concentration of 25 vol%. The hydrolysis selectivity and NDC yield of PEN were slightly higher than those of PET even if structural features would lead to the presumption that PET, as compared to the others, undergoes hydrolysis at a more rapid rate, suggesting that the high thermal stability of PEN prevented pyrolysis. Both hydrolysis selectivity and NDC yield changed only slightly at steam concentrations between 25 and 50 vol%, which is possibly attributed to the strong hydrophobicity of the naphthalene ring and the rigid structure of the PEN chain, preventing contact between the ester groups and steam.⁴³ However, the hydrolysis selectivity and NDC yield increased to 29% and 74%, respectively, at a steam concentration of 75 vol%, which is possibly attributed to overcoming the negative impact (strong hydrophobicity) of the PEN structure by the high steam concentration. In addition, the possible enhancement in acid hydrolysis by the deposited NDC is not negligible, caused by the fact that the residence time of NDC is longer than that of TPA.⁴⁴

3.3 Kinetic analysis of steam decomposition

Kinetic analyses of the steam decomposition of PET, PBT, and PEN between 350 and 400 °C and under steam concentrations of 0 and 75 vol% were conducted for the comparison of the outcomes from the ¹⁸O-labeled steam decomposition experiment. The reaction kinetics was evaluated on the basis of the weight loss caused by both hydrolysis and pyrolysis indistinctively. It was not possible to independently differentiate the weight loss contribution of each reaction because the small amount of sample did not allow for the use of the labeled ¹⁸O approach.

Fig. 5 summarizes the conversion plots of PET obtained at different isothermal temperatures under pyrolysis and at a steam concentration of 75 vol%, as one of the examples of results. The decomposition of PET was enhanced with increasing temperature and steam concentration. The same tendency was observed for the decomposition of PBT and PEN. Based on these TG results, master plots for all models under all conditions were drawn and compared with the experimental plot. Fig. 6 summarizes the experimental and master plots for each reaction model obtained from the decomposition of PET at 351 °C at a steam concentration of 75 vol%. These master plots coincided with g(α_r)/g(0.5) = 0 at α_r = 0, and g(α_r)/g(0.5) = 1 at α_r = 0.5. If there is a significant difference between the experimental observation and the master plot of each model, the models can be excluded from possible models. In Fig. 6, all power-law models and diffusion models were apparently inadequate models. In addition, chemical reaction models, except for F_1/3 (g(α_r) = 1 − (1 − α_r)^2/3) and F_3/4 (g(α_r) = 1 − (1 − α_r)^1/4), and Avrami–Eroféev models, except for A_3/2 (g(α_r) = [−ln(1 − α_r)]^2/3) were not suitable.

Fig. 5 Conversion plots of PET at different temperatures under (a) pyrolytic condition and (b) a steam concentration of 75 vol%.

Fig. 6 Experimental and master plots of each reaction model based on the results obtained at 351 °C at a steam concentration of 75 vol%. P_n: power-law models (n = 1, 2, 3, 4), R_n: phase-boundary-controlled reaction models (n = 1, 2, 3), F_n: chemical reaction models (n = 0, 1/3, 1/2, 2/3, 3/4, 1, 2, 3), A_n: Avrami–Eroféev models (n = 1, 3/2, 2, 3, 4), D_n: diffusion models (n = 1, 2, 3, 4).

Thus, possible models are narrowed down to F_1/3, F_3/4, R₂·F_1/2 (g(α_r) = 1 −(1 − α_r)^1/2), R₃·F_2/3 (g(α_r) = 1 −(1 − α_r)^1/3), and A_3/2. Possible models for other conditions and other polyesters were selected by the same procedure, and Table 1 summarizes these models. The possible models did not change for the most part regardless of steam concentration and material. In addition, the reaction order of all possible chemical reaction models was less than 1. This might be caused by the influence of the simultaneous occurrence of the sublimation of TPA and NDC with polymer decomposition as sublimation has been demonstrated to be a zero-order reaction.^45,46

Table 1 Most probable reaction models, R, E_a, and log k₀ obtained at different steam concentrations

	Steam conc. [vol%]	Possible models^a	Three best-fitting models	RModel	Eapp [kJ mol^−1]	log k0
a Determined by the reduced-time master plot method.
PET	0	F1/3, F3/4, F1, R2, F1/2, R3, F2/3	F1, A1	3.9	190.7	13.6
			F3/4	3.2	190.6	12.9
			R3, F2/3	3.0	190.6	13.0
	25	F1/3, F3/4, R2, F1/2, R3, F2/3	F3/4	3.8	183.3	12.5
			R3, F2/3	3.6	183.3	12.6
			R2, F1/2	3.1	183.2	12.8
	50	F1/3, F3/4, R2, F1/2, R3, F2/3	R3, F2/3	4.3	137.6	9.0
			R2, F1/2	4.2	137.5	9.1
			F3/4	3.9	137.6	8.8
	75	F1/3, F3/4, R2, F1/2, R3, F2/3, A3/2	R3, F2/3	4.5	139.9	9.2
			R2, F1/2	3.8	139.9	9.3
			F3/4	3.7	140.0	9.1
PBT	0	F1/3, F3/4, R2, F1/2, R3, F2/3, A3/2	A3/2	4.0	177.6	13.3
			R2, F1/2	3.8	177.5	12.9
			F1/3	3.7	177.6	13.0
	25	F1/3, F3/4, R2, F1/2, R3, F2/3, A3/2	F1/3	3.5	155.3	11.4
			R3, F2/3	3.2	154.9	11.1
			F3/4	3.1	154.8	11.0
	50	F1/3, F3/4, R2, F1/2, R3, F2/3, A3/2	A3/2	3.6	151.7	11.4
			F1/3	3.3	151.7	11.1
			R2, F1/2	3.1	151.8	11.0
	75	F1/3, F3/4, R2, F1/2, R3, F2/3, A3/2	A3/2	3.1	156.2	11.8
			F1/3	3.1	156.2	11.6
			R2, F1/2	2.7	156.0	11.5
PEN	0	F1/3, F3/4, R2, F1/2, R3, F2/3, A3/2, A2	F3/4	3.4	206.5	13.9
			R3, F2/3	3.3	207.7	14.1
			R2, F1/2	3.1	210.1	14.4
	25	F1/3, F3/4, R2, F1/2, R3, F2/3, A3/2	R3, F2/3	3.6	182.1	12.4
			F3/4	3.6	182.2	12.3
			R2, F1/2	3.3	182.0	12.5
	50	F1/3, F3/4, R2, F1/2, R3, F2/3, A3/2	R3, F2/3	3.7	175.7	11.9
			R2, F1/2	3.6	175.8	12.0
			F3/4	3.5	175.7	11.8
	75	F1/3, F3/4, R2, F1/2, R3, F2/3, A3/2	A3/2	3.7	161.1	11.3
			R2, F1/2	3.7	161.0	10.9
			F1/3	3.5	161.1	11.0

---

The possible models were further evaluated by their linearity of the plot of r_Model of t vs. g(α). Table 1 lists the reverse regression coefficient for model fitting, R_Model, of the three most probable reaction models for each condition. The three best-fitting models were well fitted, resulting in at least R_Model = 3.0 (r_Model = 0.999). The experimental error of the equipment was calculated to approximately R_Model = ±0.03, suggesting that the difference of R_Model = 0.1 is possible for considering a range of error. However, as the values of R_Model determined under the same condition were similar despite the presence and absence of experimental error, the order of the three best-fitting models might not be important. Therefore, the change in the distribution of the model with respect to the materials and steam concentration change was mainly discussed. The apparent activation energy, E_app, and the pre-exponential factor, k₀, for each model were determined by the Arrhenius plot, which are summarized in Table 1. The linearity of the Arrhenius plot was at least 0.99 for all three best-fitting models.

The best-fitting model for PET pyrolysis was the first-order chemical reaction model (F₁, g(α) = −ln(1 − α)). The apparent activation energy and log k₀ were determined to be 190.7 kJ mol⁻¹ and 13.6, respectively. These values are consistent with E_a = 197 kJ mol⁻¹ and log k₀ = 13.8 reported by Saha et al.,⁴⁷ which were also determined by fitting the F₁ model for isothermal experimental results. On the other hand, even though various E_app and k₀ values were reported from non-isothermal experiments, which are also assigned to the first-order reaction.^47–50 The reaction model shifted to phase-boundary models with increasing steam concentration. The rate-determining step of the phase-boundary model is the contraction of the reaction phase boundary. Particularly, the R₂ and R₃ models represent the contracting cylinder and sphere, respectively. Both shapes were comparable with the shape of the PET melt in the cylindrical sample holder. Hence, it suggested that hydrolysis is limited to the sample surface. The E_app and log k₀ values were dramatically reduced to 139.9 kJ mol⁻¹ and 9.2 at a steam concentration of 75 vol%, respectively. These values are higher than those previously determined under solvolytic hydrolysis,³³ because pyrolysis simultaneously occurred during steam decomposition. The reduction of E_app from 0 to 25 vol% was comparably small, whereas at 50 vol%, the lowest E_a value was observed, and higher steam concentrations exhibited no additional effect. This also indicates that the reaction mainly occurs at the sample surface. E_app decreased with increasing steam concentration until steam saturation occurred at the sample surface. The calculated log k₀ values were approximately proportional to E_app, suggesting the high reliability of the selected models and calculated kinetic values.^51,52

During the degradation of PBT, the Avrami–Eroféev models A_3/2 (where the rate-determining step is nucleation) were predominant. An Avrami order of 3/2 implied that heterogeneous spherical nucleation is predominant.^53–55 Furthermore, this observation might be caused by the lower thermal stability of PBT, resulting in the rapid evolution of gas, which led to the nucleation of gas bubbles in the polymer matrix. Moreover, the flexible structure of PBT might allow for the rapid diffusion of steam into the plastic; hence, the reaction is not limited to the sample surface. E_app and log k₀ were determined to 177.6 kJ mol⁻¹ and 13.3 under pyrolytic conditions, respectively. These values are smaller than those of PET, caused by the weaker C–O bond between the butyl groups and carboxyl oxygen in PBT.⁵⁶ These values are comparable with the published data.^57–59 E_app and log k₀ values decreased to 155.3 kJ mol⁻¹ and 11.1 at steam concentration of 25 vol%, respectively; these values remained constant even at higher steam concentrations, which is consistent with the behavior of the hydrolysis selectivity discussed in Section 3.2. The current E_app values are higher than those obtained under solvolytic hydrolysis (88 kJ mol⁻¹).⁵⁷ In addition, E_app and k₀ of PBT in the presence of steam were higher than those of PET, suggesting the strong influence of pyrolysis on steam decomposition.

The most probable model for PEN pyrolysis was F_3/4, resulting in E_app = 206.5 kJ mol⁻¹ and log k₀ = 13.9. These values are comparatively lower than those calculated from the non-isothermal method,⁶⁰ which is similar to the tendency exhibited by PET. With the addition of steam, the reaction model shifted to the phase-boundary-controlled reaction models R₂ and R₃. The reaction of PEN resembles that of PET, with the reaction limited to the sample surface, caused by the rigid and hydrophobic PEN structure. Under pyrolytic conditions, E_app decreased from 206.5 kJ mol⁻¹ to 182.1 kJ mol⁻¹ at a steam concentration of 25 vol%. Moreover, at a steam concentration of 50 vol%, E_app slightly decreased to 175.7 kJ mol⁻¹, while at a steam concentration of 75 vol%, it further decreased to 161.1 kJ mol⁻¹. This behavior is consistent with the hydrolysis selectivity obtained in Section 3.1. These E_app values are higher than those obtained under solvolytic hydrolysis (110–120 kJ mol⁻¹),⁶¹ caused by the influence of pyrolysis. The higher E_app for both pyrolysis and hydrolysis during the decomposition of PEN as compared to that of PET and PBT is attributed to the higher thermal stability of the PEN structure.

Common reaction models such as F_1/3, F_3/4, R₂ (F_1/2), and R₃ (F_2/3) were selected by the reduced-time master plot method under all conditions. In these models, F_3/4 was the best-fitted (r_Model > 0.99) common reaction model under all conditions. Thus, the k_app values of each material at each set of conditions were calculated using F_3/4 and plotted in Fig. 7. As a side note, k_app values calculated using other possible models also exhibited the same behavior even though k_app values differed according to the selected model. Thus, we concluded that the F_3/4 model is appropriate for discussing k_app behavior.

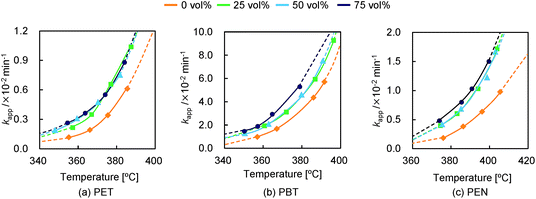Fig. 7 Apparent reaction constant k_app calculated using reaction model F_3/4 at different steam concentrations: (a) PET, (b) PBT, and (c) PEN.

It was assumed that k_app values estimated through the F_3/4 model using data from reactions in the absence of steam were equivalent to the k_app of pyrolysis. The k_app of pyrolysis during the decomposition of PET increased at an accelerated pace along with the increase of reaction temperature (Fig. 7 (a)). k_app also increased when steam was added. This increment can be considered to correspond to hydrolysis; thus, the difference between the k_app of pyrolysis and the k_app of steam decomposition can be assumed to be the k_app of hydrolysis (assuming whole k_app = pyrolysis k_app + hydrolysis k_app). Fig. 8(a) plots the k_app of hydrolysis at 75 vol%. Interestingly, the hydrolysis rate did not significantly change in the investigated temperature range, suggesting that the hydrolysis rate is insensitive at these temperatures. Hence, this result reveals the presence of a crossing point at which the dominant reaction changes from hydrolysis to pyrolysis. The influence of the steam concentration on the hydrolysis rate is more obvious at lower temperatures as the influence of pyrolysis is comparatively weak. The behavior of both pyrolysis and hydrolysis rates observed in this section is well reflected in the selectivities for both processes obtained in Sections 3.1 and 3.2. The crossing-point temperatures observed in the ¹⁸O-labeling experiments and kinetic analyses were slightly different because steam contact efficiency was not identical for different instruments.

Fig. 8 Pyrolysis and hydrolysis behavior of (a) PET, (b) PBT, and (c) PEN during the investigated temperature range at a steam concentration of 75 vol%.

The behavior of the k_app of PBT was similar to that of PET, although the reaction rate was significantly higher, caused by the lower stability of PBT (Fig. 7(b)). The k_app of PBT pyrolysis was accelerated with increasing temperature, similar to PET. k_app was enhanced when steam was added, although it is unclear if there is any influence of steam concentration on the hydrolysis rate. The hydrolysis rate for PBT (Fig. 8(b)), similar to that for PET, was not sensitive to change in temperature. Hence, the dominant reaction changed from hydrolysis to pyrolysis with increasing reaction temperature. The selectivities obtained in Sections 3.1 and 3.2 are attributed to the changes in both pyrolysis and hydrolysis rates.

The k_app increase for pyrolysis during the decomposition of PEN was comparatively linear over the investigated temperature range (Fig. 7(c)). This might be caused by the high thermal stability of the PEN structure. On the other hand, the k_app of steam decomposition increased at an accelerated pace with increasing reaction temperature. Thus, both pyrolysis and hydrolysis rates were comparable through the investigated temperature range at a steam concentration of 75 vol% (Fig. 8(c)). The rigid PEN structure is expected to become flexible with increasing temperature, resulting in higher access of steam to the ester bonds. In addition, NDC might catalyze hydrolysis, caused by the fact that it exhibits vapor pressure lower than that of TPA. The pyrolysis and hydrolysis behavior correlated well with the selectivities obtained in Section 3.1. The enhancement of both rates results in constant selectivities for pyrolysis and hydrolysis with decreasing NDC. In addition, k_app did not exhibit any effect at steam concentrations between 25 and 50 vol%. However, k_app under a steam concentration of 75 vol% clearly increased. This behavior is consistent with the results obtained in section 3.2.

4. Conclusions

In this study, ¹⁸O-labeling experiments and kinetic analyses were conducted at different steam concentrations and reaction temperatures for investigating the pyrolysis-versus-hydrolysis behavior during the steam decomposition of PET, PBT, and PEN. The selectivity for hydrolysis during the decomposition of PET and PBT dramatically decreased with increasing temperature, caused by the acceleration of the pyrolysis rate. In contrast, both selectivities during the decomposition of PEN remained nearly constant over the investigated temperature range caused by the high thermal stability of the PEN structure, resulting in the simultaneous acceleration of pyrolysis and hydrolysis. An increase in the steam concentration improved the hydrolysis selectivity during the decomposition of PET and PEN, whereas no comparable effect was observed during the decomposition of PBT because of the competitive pyrolysis process. These results reveal that the selectivities between pyrolysis and hydrolysis during the steam decomposition of polyesters are significantly influenced by their molecular structure.

This study will be helpful toward the further improvement of the accuracy of the kinetic analyses of pyrolysis and hydrolysis and identification of the best conditions for the maximum process efficiency. Hydrolysis-predominant conditions are suitable for maximizing monomer yields, even with a lower reaction rate. In contrast, pyrolysis-predominant conditions enhance the complete reaction rate, which is suitable for reducing the reaction time. The results herein imply that these techniques can be applied for the evaluation of other transformations of polycondensation polymer, such as those of polycarbonates, polyamides, and polyimides.

Acknowledgements

This study was partially supported by the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Grant-in-Aid for Scientific Research (A) (no. 25241022), and the Japan Society for the Promotion of Science (JSPS), Grant-in-Aid for JSPS Fellows, 24-4996.

Notes and references

1. J. R. Campanelli, D. G. Cooper and M. R. Kamal, J. Appl. Polym. Sci., 1993, 48, 443.
2. T. Adschiri, O. Sato, K. Machida, N. Saito and K. Arai, Kagaku Kogaku Ronbunshu, 1997, 23, 505.
3. T. Masuda, Y. Miwa, A. Tamagawa, S. R. Mukai, K. Hashimoto and Y. Ikeda, Polym. Degrad. Stab., 1997, 58, 315.
4. T. Yoshioka, N. Okayama and A. Okuwaki, Ind. Eng. Chem. Res., 1998, 37, 336.
5. M. Dzieciol and J. Trzeszczynski, J. Appl. Polym. Sci., 2001, 81, 3064.
6. T. Yoshioka, T. Motoki and A. Okuwaki, Ind. Eng. Chem. Res., 2001, 40, 75.
7. G. P. Karayannidis, A. P. Chatziavgoustis and D. S. Achilias, Adv. Polym. Technol., 2002, 21, 250.
8. A. S. Goje, Y. P. Chauhan and S. Mishra, Polym.-Plast. Technol. Eng., 2004, 43, 95.
9. G. Grause, W. Kaminsky and G. Fahrbach, Polym. Degrad. Stab., 2004, 85, 571.
10. T. Yoshioka, G. Grause, C. Eger, W. Kaminsky and A. Okuwaki, Polym. Degrad. Stab., 2004, 86, 499.
11. T. Yoshioka, E. Kitagawa, T. Mizoguchi and A. Okuwaki, Chem. Lett., 2004, 33, 282.
12. T. Yoshioka, T. Handa, G. Grause, Z. Lei, H. Inomata and T. Mizoguchi, J. Anal. Appl. Pyrolysis, 2005, 73, 139.
13. O. Sato, K. Arai and M. Shirai, Catal. Today, 2006, 111, 297.
14. R. Arai, K. Zenda, K. Hatakeyama, K. Yui and T. Funazukuri, Chem. Eng. Sci., 2010, 65, 36.
15. M. Artetxe, G. Lopez, M. Amutio, G. Elordi, M. Olazar and J. Bilbao, Ind. Eng. Chem. Res., 2010, 49, 2064.
16. G. Grause, T. Handa, T. Kameda, T. Mizoguchi and T. Yoshioka, J. Appl. Polym. Sci., 2011, 120, 3687.
17. G. Grause, T. Handa, T. Kameda, T. Mizoguchi and T. Yoshioka, Chem. Eng. J., 2011, 166, 523.
18. L. Zhang, Eur. Polym. J., 2014, 60, 1.
19. X.-K. Li, H. Lu, W.-Z. Guo, G.-P. Cao, H.-L. Liu and Y.-H. Shi, AIChE J., 2015, 61, 200.
20. A. S. Goje, Y. P. Chauhan and S. Mishra, Chem. Eng. Technol., 2004, 27, 790.
21. A. S. Goje, Polym.-Plast. Technol. Eng., 2006, 45, 171.
22. T. Yoshioka, G. Grause, S. Otani and A. Okuwaki, Polym. Degrad. Stab., 2006, 91, 1002.
23. O. Sato, K. Arai and M. Shirai, Fluid Phase Equilib., 2005, 228–229, 523.
24. I. Goodman and B. F. Nesbitt, Polymer, 1960, 1, 384.
25. U. Hujuri, A. K. Ghoshal and S. Gumma, J. Appl. Polym. Sci., 2013, 130, 3993.
26. G. Montaudo, Macromolecules, 1991, 24, 5829.
27. G. Montaudo, C. Puglisi and F. Samperi, Polym. Degrad. Stab., 1993, 42, 13.
28. F. Samperi, C. Puglisi, R. Alicata and G. Montaudo, Polym. Degrad. Stab., 2004, 83, 3.
29. L. H. Buxbaum, Angew. Chem., Int. Ed., 1968, 7, 182.
30. I. C. Mcneill and M. Bounekhel, Polym. Degrad. Stab., 1991, 34, 187.
31. D. A. S. Ravens and I. M. Ward, Trans. Faraday Soc., 1961, 57, 150.
32. H. Zimmerman and N. T. Kim, Polym. Eng. Sci., 1980, 20, 680.
33. V. S. Zope and S. Mishra, J. Appl. Polym. Sci., 2008, 110, 2179.
34. S. Kumagai, G. Grause, T. Kameda and T. Yoshioka, Environ. Sci. Technol., 2014, 48, 3430.
35. G. Grause, S. Matsumoto, T. Kameda and T. Yoshioka, Ind. Eng. Chem. Res., 2011, 50, 5459.
36. S. Kumagai, Y. Morohoshi, G. Grause, T. Kameda and T. Yoshioka, Chem. Lett., 2013, 42, 212.
37. B. Janković and B. Adnađević, Int. J. Chem. Kinet., 2007, 39, 462.
38. A. I. Lesnikovich and S. V. Levchik, J. Therm. Anal. Calorim., 1985, 30, 677.
39. L. Vlaev, N. Nedelchev, K. Gyurova and M. Zagorcheva, J. Anal. Appl. Pyrolysis, 2008, 81, 253.
40. G. Grause, J. Ishibashi, T. Kameda, T. Bhaskar and T. Yoshioka, Polym. Degrad. Stab., 2010, 95, 1129.
41. F. J. Gotor, J. M. Criado, J. Malek and N. Koga, J. Phys. Chem. A, 2000, 104, 10777.
42. J. H. Sharp, G. W. Brindley and B. N. N. Achar, J. Am. Ceram. Soc., 1966, 49, 379.
43. CRC, Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, 1995.
44. C.-Y. Kao, B.-Z. Wan and W.-H. Cheng, Ind. Eng. Chem. Res., 1998, 37, 1228.
45. C. D. Doyle, J. Appl. Polym. Sci., 1961, 5, 285.
46. D. Dollimore, Thermochim. Acta, 1999, 340–341, 19.
47. B. Saha and A. K. Ghoshal, Ind. Eng. Chem. Res., 2006, 45, 7752.
48. I. Martin-Gullon, M. Esperanza and R. Font, J. Anal. Appl. Pyrolysis, 2001, 58–59, 635.
49. J. Yang, R. Miranda and C. Roy, Polym. Degrad. Stab., 2001, 73, 455.
50. J. Li and S. I. Stoliarov, Polym. Degrad. Stab., 2014, 106, 2.
51. N. Koga and H. Tanaka, Thermochim. Acta, 1988, 135, 79.
52. H. Tanaka and N. Koga, J. Therm. Anal., 1988, 34, 685.
53. M. Avrami, J. Chem. Phys., 1939, 7, 1103.
54. M. Avrami, J. Chem. Phys., 1940, 8, 212.
55. M. Avrami, J. Chem. Phys., 1941, 9, 177.
56. T. Ueno, T. Kajiya, T. Ishikawa and K. Takeda, Kobunshi Ronbunshu, 2007, 64, 575.
57. M. Tanaka and S. Nakazawa, Sen'i Gakkaishi, 1987, 43, 370.
58. P. E. Sánchez-Jiménez, L. A. Pérez-Maqueda, A. Perejón and J. M. Criado, Polym. Degrad. Stab., 2010, 95, 733.
59. V. Passalacqua, F. Pilati, V. Zomboni, B. Fortunato and P. Manaresi, Polymer, 1976, 17, 1044.
60. S. R. Mohammadi, H. A. Khonakdar, M. Ehsani, S. H. Jafari, U. Wagenknecht and B. Kretzschmar, J. Polym. Res., 2011, 18, 1765.
61. H. Zhang and I. M. Ward, Macromolecules, 1995, 28, 7622.

---