C-doped boron nitride fullerene as a novel catalyst for acetylene hydrochlorination: a DFT study

Abstract

Density functional theory calculations were used to investigate the mechanism of acetylene hydrochlorination separately catalyzed by un-doped B₁₂N₁₂ and carbon-doped BN fullerene (B_12−nN_11+nC (n = 0, 1)). We have discovered that carbon-doped BN clusters displayed extraordinary catalyst performance for acetylene hydrochlorination compared with un-doped B₁₂N₁₂ clusters. C₂H₂ was adsorbed onto B_12−nN_11+nC (n = 0, 1) clusters prior to HCl and then formed three adsorption states. The first two states were in a trans configuration, in which the two H atoms of C₂H₂ were on opposite sides of the C=C bond; the third state was a cis configuration, in which the two H atoms were on the same side of the C=C bond. Afterwards, we illustrated three possible pathways with corresponding transition states. In particular, the minimum energy pathway R1 based on the B₁₁N₁₂C catalyst had an energy barrier as low as 36.08 kcal mol⁻¹, with only one transition state.

---

1. Introduction

Not long after the discovery of C₆₀ by Kroto et al. in 1985,¹ research on fullerene and related materials boomed. With the first case of successful preparation of doped fullerene,² investigators have extensively researched the preparation, structure, and application of various doped fullerenes.^3–11 Among these doped fullerenes, the B₁₂N₁₂ cage is considered to be the smallest stable cage.^6,12,13 B₁₂N₁₂ cages were successfully synthesized by Oku et al. in 2004 and were analyzed by laser desorption time-of-flight mass spectrometry.^6,14 Their research revealed that B₁₂N₁₂ clusters consisting of four- and six-membered BN rings satisfy the isolated tetragonal rule. Although scientists have widely explored the usage of these clusters as catalysts, many studies have concentrated on their application as hydrogen-storage materials^8,9,15,16 and have neglected their potential roles in other reactions. In the present work, doped BN fullerene was used as a catalyst for acetylene hydrochlorination for the first time.

Mercuric chloride is the most commonly used catalyst for the industrial production of vinyl chloride monomer. However, mercuric chloride catalyst easily sublimes at high temperatures^17,18 and seriously harms human health and the environment. Therefore, possible alternatives that are efficient and environment friendly are necessary. In 1985,¹⁹ Hutchings et al. predicted that gold-based catalysts could be greener substitutes for mercuric chloride. They performed an experiment²⁰ to confirm that Au³⁺ possesses the highest catalytic activity among the selected metal complexes containing Bi³⁺,²¹ Pd²⁺,²² Pt²⁺,²³ and Pt⁴⁺.²⁴ However, the supported gold catalysts were more easily deactivated with prolonged reaction time because the active gold species Au³⁺ is reduced to Au⁰.²⁵ To overcome this difficulty, J. Zhang et al. studied the deactivation mechanism of AuCl₃ catalyst through the AuCl₃ dimer model and density functional theory (DFT).²⁶ M. Zhu et al. developed various methods to enhance the activation and stability of Au³⁺ by preparing AuCl₃/PPy–MWCNTs catalysts.^27–29 L. Kang et al. investigated the reaction mechanism of the hydrochlorination of acetylene to C₂H₃Cl over MCl_x (M = Hg, Au, Ru; x = 2, 3) catalyst. They concluded that RuCl₃ could be a good candidate catalyst based on theoretical calculations.³⁰ Other scientists have researched the mechanisms, active sites, and deactivation.^31–33 Most of the reported studies are focused on metal chloride catalysts,^34–38 and research on non-metallic catalysts, especially C-doped BN cages, for acetylene hydrochlorination is limited.^39–43

In the present study, DFT was used to study the adsorption and dissociation of C₂H₂ and HCl on un-doped B₁₂N₁₂ and C-doped B_12−nN_11+nC (n = 0, 1) cages, respectively. The mechanisms of acetylene hydrochlorination to vinyl chloride catalyzed by BNC (B_12−nN_11+nC (n = 0, 1)) cages were examined. These investigations on the reaction mechanism of acetylene hydrochlorination on BN cages can aid the design of new environmentally benign, non-mercury catalysts and facilitate the sustainable development of the polyvinyl chloride industry.

2. Computational methods

All DFT calculations were executed using the Guassian09 program package.⁴⁴ No symmetry constraints were imposed on the geometry optimization. The hybrid density functionals of Lee, Yang and Parr (B3LYP)⁴⁵ with the 6-31+G** basis set were applied for all structures, including reactants, products, intermediates, and transition states. All stationary points mentioned were characterized as minima (no imaginary frequency) or transition states (one imaginary frequency) through a Hessian calculation. Intrinsic reaction coordinate (IRC)^46,47 calculations were performed to confirm that the reaction links the correct products to the reactants. Transition-state structures were characterized using frequency calculations and by analyzing the vibrational modes. In all instances, only one imaginary frequency corresponding with the reaction coordinate was obtained. Basis set superposition error⁴⁸ corrections evaluated by the counterpoise method were considered.

Considering frontier molecular orbital (FMO) and charge-distribution analysis, we can estimate the approximate distribution of the active sites of the BNC cages, as well as the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) energies of the C₂H₂, HCl, and BNC cages. By calculating the HOMO–LUMO energy gaps, we obtained the lowest HOMO–LUMO energy gaps and ascertained the electron donor and acceptor. We have further verified the predicted consequence of FMO analysis through charge-distribution analysis.

3. Results and discussion

3.1. Geometries of reactants and adsorption onto BNC cages

3.1.1. Geometries of reactants. The reactants included isolated C₂H₂ molecules, HCl molecules, un-doped B₁₂N₁₂, and the corresponding C-doped B_12−nN_11+nC (n = 0, 1) cages. Fig. 1 displays the optimized structure of the reactants. The B₁₂N₁₂ cage is the smallest stable BN fullerene among all known BN cages.^3,6 All B or N sites are equivalent with Th symmetry for cages composed of alternately distributed boron and nitrogen atoms. Considering this cage from a structure perspective, the B₁₂N₁₂ cage (shown in Fig. 1(a)) is composed of six 4-membered rings (4-MR) and eight 6-membered rings (6-MR). The B–N bonds were of two types: one was shared by two adjacent 6-MRs with the lengths of 1.439 Å, and the other was shared by a 4-MR and a 6-MR with lengths of 1.487 Å. The charges were uniformly distributed on the B₁₂N₁₂ cage with a Mulliken value of 0.57 for B atoms and −0.57 for N atoms.

Fig. 1 Optimized structures of C₂H₂, HCl, un-doped B₁₂N₁₂ cluster (a), carbon-doped B₁₁N₁₂C (b) and B₁₂N₁₁C (c) cluster. Distances are in Å and angles are in °. Chlorine, carbon, boron, nitrogen and hydrogen atoms are depicted in blue-green, gray-green, pink, blue and silver-gray, respectively.

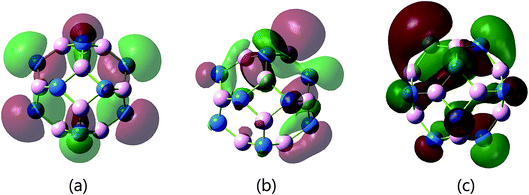
By separately substituting one C atom for a B or N atom in B₁₂N₁₂, B₁₁N₁₂C and B₁₂N₁₁C were obtained. As shown in the HOMO in Fig. 2(b), electrons accumulated around the C1 atom in B₁₁N₁₂C, as well as in B₁₂N₁₁C (Fig. 2(c)). The charges of the C1 atom in B₁₁N₁₂C and B₁₂N₁₁C were −0.812 and −0.023, respectively. As a result, C-doping lengthened the adjacent C1–N3 bond from 1.439 Å to 1.418 Å (Fig. 1(b)) and the C1–B3 bond to 1.546 Å in B₁₂N₁₁C (Fig. 1(c)), which made the C1 atom appear slightly embossed. The Mulliken charges of the C1 atom were −0.81 in B₁₁N₁₂C and −0.023 in B₁₂N₁₁C. The C1 site was more active than any other site in the cages.

Fig. 2 The calculated HOMO for B₁₂N₁₂ (a), B₁₁N₁₂C (b) and B₁₂N₁₁C (c) at B3LYP/6-31+G** level. According to the introduction of carbon, the electrons redistribute on BN clusters and accumulate around the C1 atom in B₁₁N₁₂C, as well as for B₁₂N₁₁C. These figures will contribute to the prediction of adsorption cite.

3.1.2. Adsorption of acetylene and hydrogen chloride onto BNC cages. Fig. 5 and Table 2 illustrate the weak adsorption of C₂H₂ and HCl onto the B₁₂N₁₂ cage. In Fig. 5, the distance between the adsorbate and the B₁₂N₁₂ cage was longer than 2 Å, reaching more than 3 Å for C₂H₂. Moreover, neither obvious change in bond length nor distortion in shape of the B₁₂N₁₂ cage and adsorbate was observed, indicating that C₂H₂ and HCl molecules were physically adsorbed onto the B₁₂N₁₂ cage. The adsorption energies (E_ad) were calculated by eqn (1).

E_ad = E_{adsorption state} − (E_reactant + E_catalyst) (1)

Table 2 shows the adsorption energies of C₂H₂ and HCl on the nanocages. The adsorption energies of C₂H₂ and HCl onto B₁₂N₁₂ were very low, suggesting that C₂H₂ and HCl cannot stably adsorb onto the B₁₂N₁₂ cage and be efficiently activated by catalyst.

Table 1 and Fig. 3 list the orbital energies of the HOMOs and LUMOs of C₂H₂, HCl, B₁₂N₁₂, B₁₁N₁₂C, and B₁₂N₁₁C, as well as their energy gaps. The energy gaps of the HOMO–LUMO (C₂H₂ → BNC) were smaller than those of the HOMO–LUMO (BNC → C₂H₂), indicating that C₂H₂ was an electron donor. In contrast to C₂H₂, the energy gaps of HOMO–LUMO (HCl → BNC) were larger than those of HOMO–LUMO (BNC → HCl), indicating that HCl was an electron acceptor. The energy gaps represented the ability of electrons to transfer from C₂H₂/HCl to the BNC cages. Fig. 3 clearly shows that the energy gaps of HOMO–LUMO (C₂H₂ → BNC) were smaller than those of HOMO–LUMO (HCl → BNC). Thus, we can predict that acetylene was better adsorbed onto the BNC cages than HCl, as verified by comparing adsorption energies.

Table 1 The orbital energies on the HOMO and LUMO of C₂H₂, HCl, B₁₂N₁₂, B₁₁N₁₂C and B₁₂N₁₁C, and their energy gaps between C₂H₂, HCl and BNC (B_12−nN_11+nC (n = 0, 1)) cages (energies in eV, isovalue = 0.02)

			HOMO–LUMO	HOMO–LUMO	HOMO–LUMO	HOMO–LUMO	HOMO–LUMO
			(BNC → C2H2)	(BNC → HCl)	(C2H2/HCl → B12N12)	(C2H2/HCl → B11N12C)	(C2H2/HCl → B12N11C)
	HOMO	LUMO	C2H2	HCl	B12N12	B11N12C	B12N11C
C2H2	−8.08	0.35			6.84	5.81	7.62
HCl	−9.19	−0.42			7.95	6.92	8.73
B12N12	−7.95	−1.24	8.30	7.53
B11N12C	−5.76	−2.27	6.11	5.34
B12N11C	−7.43	−0.46	7.78	7.01

---

Fig. 3 The energy gaps of HOMO–LUMO between adsorbates (C₂H₂ and HCl) and BNC clusters are illustrate in this figure for intuitive understanding. Further detail data is provides in Table 1.

The corresponding adsorption energies of C₂H₂ and HCl adsorbed onto BNC cages are displayed in Fig. 4. Besides, Table 2 lists the optimal adsorption energies of C₂H₂ and HCl onto the BNC cages. We can clearly observe that C₂H₂ was more easily adsorbed onto BNC than HCl, which confirmed the previous prediction obtained by the HOMO–LUMO energy gaps. These cages primarily adsorbed C₂H₂ to form BNC-C₂H₂ complexes, which subsequently adsorbed HCl because of the considerable difference in the adsorption energies of C₂H₂ and HCl. This conclusion was the same as that drawn from the HOMO–LUMO energy gap analysis.

Fig. 4 The adsorption energies of C₂H₂ and HCl separately adsorbed on BN clusters. We can easily conclude that the introduction of carbon on B₁₂N₁₂ could improve the ability of C₂H₂ and HCl adsorb on B₁₂N₁₂ (energies in kcal mol⁻¹).

Table 2 The optimal adsorption energies of C₂H₂ and HCl separately adsorb on BNC (B_12−nN_11+nC (n = 0, 1)) cages (energies in kcal mol⁻¹)

	B12N12	B11N12C	B12N11C
C2H2	−0.79	−25.70	−27.58
HCl	−0.50	−3.06	−0.16

---

To identify the most favorable adsorption configurations on the B₁₁N₁₂C and B₁₂N₁₁C cages, a C₂H₂ molecule was originally placed in different sites on the surface of the nanocages with different directions. We obtained the three most stable single-component adsorption configurations (A, B, and C), as shown in Fig. 5. A and B corresponds to a C₂H₂ molecule adsorbed onto a B₁₁N₁₂C cage, and C was corresponds to a C₂H₂ molecule adsorbed onto a B₁₂N₁₁C cage. Fig. 5(A and B) show that the C₂H₂ adsorbed onto the B₁₁N₁₂C cage in a different way, i.e., in the trans configuration for A and in the cis configuration for B. This subtle distinction considerably influenced the mechanism, as elaborated in the next part. Given that the π molecular orbital of C₂H₂ transferred to the BNC cages, the C≡C triple bond became a double bond, and the bond length increased from 1.208 Å to 1.312, 1.312, and 1.317 Å. A C–C single bond formed between the C2 atom of acetylene and the C1 atom of the BNC cage, and the bond lengths were 1.513, 1.506, and 1.517 Å, respectively. More distortions were observed in the angles of the C₂H₂ molecule, which revealed that C₂H₂ molecular was well-activated. These results further demonstrated that C-doped B_12−nN_11+nC (n = 0, 1) fullerenes had considerable sorption capacity and that the C1 site had high activity.

Fig. 5 The first two structures are C₂H₂ and HCl physical adsorb on B₁₂N₁₂ cage. A, B and C are corresponding to the three most stable adsorption configurations of C₂H₂ adsorb on B₁₁N₁₂C and B₁₂N₁₁C, respectively. All distances are in Å and angles are in °. Chlorine, carbon, boron, nitrogen and hydrogen atoms are depicted in blue-green, gray-green, pink, blue and silver-gray, respectively.

3.2. Reaction mechanisms of acetylene hydrochlorination over BNC cages

The possible reaction pathways were systematically examined to gain a better understanding of the reaction mechanism of B₁₁N₁₂C and B₁₂N₁₁C catalyzing the reaction of acetylene hydrochlorination. Fig. 6 shows the reaction pathways starting from HCl and C₂H₂ co-adsorption structures (Fig. 5(A, B, and C)) denoted as R1, R2, and R3, respectively. The structures of the various stationary points located on the potential energy surface are depicted in Fig. 7–9, along with the values of the most relevant geometrical parameters.

Fig. 6 The energy profiles for the different reaction pathways R1, R2 and R3 of acetylene hydrochlorination over the BNC (B_12−nN_11+nC (n = 0, 1)) cages. R1, R2 and R3 are separately start from adsorption complex A, B and C (energies in kcal mol⁻¹).

Fig. 7 Optimized structures of stationary points for reaction channel R1. The blue arrow presents the direction of vibration of H1 atom. All distances are in Å and angles are in °.

3.2.1. Reaction mechanism of R1. The reaction pathway started with the structure of C₂H₂ adsorbing onto B₁₁N₁₂C, as shown in Fig. 5(A). The adsorption configurations were of two types, i.e., cis- and trans-adsorption structures. The co-adsorption energy of the former was −28.39 kcal mol⁻¹, which was slightly higher than the −28.45 kcal mol⁻¹ of the latter. Accordingly, we considered that the trans-form resulted in a shorter reaction pathway and a significantly lower activation barrier of 36.08 kcal mol⁻¹ in pathway 1 than the 49.63 kcal mol⁻¹ in pathway 2. Therefore, only one transition state existed for pathway 1.

The HCl molecule subsequently adsorbed onto the C₂H₂–B₁₁N₁₂C complex to form a co-adsorption configuration. Considering the changes in the bond length and adsorption energy, HCl was nearly unactivated in the co-adsorption state. The co-adsorption structure can be converted into the de-adsorption structure through the transition state Ts1 (Fig. 7). In the Ts1 state, the HCl molecule shifted to the other side of the C=C double bond and closer to the C=C double bond. Meanwhile, the bond length of H–Cl increased from 1.306 Å to 1.877 Å compared with the co-adsorption state. The H1 atom approached the C2 atom, and the distance between them decreased to 1.355 Å. This finding proved that the HCl molecule completely dissociated and was activated in the Ts1 state. Only one imaginary frequency (−1090.30 cm⁻¹) was obtained from the vibrational analysis of the Ts1 structure. This frequency was associated with the stretching movement of the H1 atom. To achieve the Ts1 state, a climb over the energy barrier of 36.08 kcal mol⁻¹ (the activation energy of acetylene hydrochlorination) was required. This step was the rate-limiting step. To evaluate the catalyst activity of B₁₁N₁₂C in acetylene hydrochlorination, we compared the energy barrier in the rate-limiting step on B₁₁N₁₂C with other calculated non-metal catalysts (Table 3). The results showed that B₁₁N₁₂C performed well.

Table 3 Comparison of the energy barriers for acetylene hydrochlorination in rate-limiting step obtained with different catalysts (energies in kcal mol⁻¹)

Catalyst	Energy barrier (kcal mol^−1)	Ref.
B11N12C	36.08	This work (R1)
AuCl3	11.86	30
g-C3N4/AC	77.94	39
PSAC-N	28.83	41
NCNT	32.52	42

---

To gain a better understanding of the reaction mechanism, an IRC calculation was performed to confirm that the transition state structure linked the co-adsorption complex to the de-adsorption complex. No further intermediates were involved in the reactions. In the de-adsorption state, the target product C₂H₃Cl molecule adsorbed onto B₁₁N₁₂C cages to form adsorption complexes. The bond length of the calculated C2–C3 was 1.488 Å, longer than the 1.329 Å of the free C₂H₃Cl molecule. The final step was the desorption of C₂H₃Cl molecules, and the desorption energy was 25.41 kcal mol⁻¹, which was equal to the adsorption energy of the C₂H₃Cl molecule onto the B₁₁N₁₂C cage.

3.2.2. Reaction mechanism of R2 and R3. In view of the resemblance between the mechanisms of R2 and R3 (Fig. 8 and 9), we combined the two mechanisms for simplicity of explanation. Similar to R1, the C₂H₂ molecule was firstly chemisorbed onto the B₁₁N₁₂C and B₁₂N₁₁C cages, and then the HCl molecule continued to adsorb onto the C₂H₂–B₁₁N₁₂C and C₂H₂–B₁₂N₁₁C complexes to form co-adsorption structures. However, they physically adsorbed onto the complexes because of the weak interaction between the HCl molecule and the C-doped BN cage. The bond lengths of C1–C2, C2–C3, and H1–Cl were only very slightly changed, further confirming that HCl was unactivated.

Fig. 8 Optimized structures of stationary points for reaction channel R2. It has the same De-ads and Pr state with R1. The blue arrow presents the direction of vibration of H1 atom. All distances are in Å and angles are in °.

The structure of co-adsorption can change to Ims1 with transition state Ts1. In this structure, the H1–Cl bond was substantially lengthened and induced the elimination of thee HCl molecule. The H1–Cl bond length increased from 1.302 Å to 1.517 Å compared with the co-adsorption state in R2. A significant change in the coordination of the HCl molecule also occurred. The Cl atom approached the C2 site in R2, and the distance between them decreased from 3.647 to 1.988 Å compared with the co-adsorption state, indicating that HCl was completely activated. We observed an interesting phenomenon about the Ts1 state (Fig. 9) in R3. The H–Cl bond was not only broken but also nearly adsorbed in parallel onto the C=C bond and formed a dihedral angle of 0.883 between the H1–Cl and C2–C3 atoms. At the same time, the H–Cl bond length increased from 1.306 Å to 1.552 Å, but the other critical bonds, such as C1–C2 and C2–C3, underwent only very slight changes.

Fig. 9 Optimized structures of stationary points for reaction channel R3. The blue arrow presents the direction of vibration of H1 atom. All distances are in Å and angles are in °.

The only imaginary frequency (−2480 cm⁻¹ in R2 and −1780.75 cm⁻¹ in R3) was obtained from the vibrational analysis of the Ts1 structure. This phenomenon was associated with the stretching movement of the H1 atom. To achieve the Ts1 state, a climb over the energy barriers of 49.63 and 41.41 kcal mol⁻¹ (the activation energy of acetylene hydrochlorination) was required. This step was the rate-controlling step for both pathways.

To gain a better understanding of the reaction mechanism, an IRC calculation was performed for co-adsorption conversion to Ims1. The IRC calculation confirmed that the Ts1 state linked the co-adsorption and Ims1 states. In the Ims1 state, a C3–Cl bond was formed by the attraction of the C3 atom. Fig. 8 and 9 show that the HCl molecule dissociated in Ts1, and the Cl atom and the nearest C3 atom had opposite charges. The charges of the Cl atom were 0.089 in R2 and 0.129 in R3. The C3 atom had opposite charges of −0.163 in R2 and −0.070 in R3. The interaction between the opposite charges caused the chlorine atom to transfer from HCl to the C3 site of the C₂H₂–B₁₁N₁₂C complex to form a C3–Cl bond in the Ims1 state. The distance between the C3 and Cl atom decreased from 1.988 Å to 1.745 Å in R2 and 1.753 Å in R3 compared with the Ts1 state.

The intermediate state Ims1 can generate a de-adsorption product with transition state Ts2. In the Ts2 state of both pathways, the H1 atom that separated from the HCl molecule almost perpendicularly approached the C2 site. The distance between the C2 and H1 atoms was 2.169 Å in R2 and 2.09 Å in R3. The only imaginary frequency (475.15 cm⁻¹ in R2 and −459.88 cm⁻¹ in R3) was obtained from the vibrational analysis of the Ts2 structure, which was associated with the stretching movement of the H1 atom. To obtain the Ts2 state of R2, the Ims1 state required climbing over an energy barrier of only 1.4 kcal mol⁻¹. The corresponding energy barrier of R3 was 1.34 kcal mol⁻¹. Thus, the H1 atom was easily attracted by the C₂H₂Cl–B_12−nN_11+nC (n = 0, 1) complex.

IRC calculation was performed again to confirm that the Ts2 state can convert into the de-adsorption state, in which the target product C₂H₃Cl molecule adsorbed onto B_12−nN_11+nC (n = 0, 1) cages to form adsorption complexes. In spite of the different adsorption configurations in R1 and R2, the same de-adsorption configuration was formed. In the de-adsorption state of R3, the bond length of the calculated C2–C3 was 1.489 Å, longer than 1.329 Å in the free C₂H₃Cl molecule. The final step was the desorption of the C₂H₃Cl molecule, and the desorption energy in R3 was 23.98 kcal mol⁻¹, which was equal to the adsorption energy of the C₂H₃Cl molecule adsorbed onto the B₁₂N₁₁C cage.

4. Conclusions

According to our DFT calculations at the B3LYP/6-31+G** level, the doping of C atoms on the BN cages can significantly intensify the adsorption ability of the C₂H₂ molecule compared with the un-doped BN cages. The first step of the reaction was C₂H₂ adsorption, and the rate-limiting step was the dissociation of the HCl molecule in the TS1 state. In addition, we found that the trans-adsorption of the C₂H₂ molecule on the B₁₁N₁₂C cage was more favorable for acetylene hydrochlorination than cis-adsorption. Trans-adsorption can efficiently reduce the activation barrier and shorten the reaction pathway. The energy barrier for H1–Cl scission in pathway R1 was much lower than those in R2 and R3, suggesting that acetylene hydrochlorination much more easily occurred than in R1 and R3. Our investigations indicated that B₁₁N₁₂C performed well among non-metal catalysts and can be a candidate catalyst for acetylene hydrochlorination. We hope that our results can be useful for designing and developing novel nonmetallic catalysts.

Acknowledgements

We gratefully acknowledge the National Natural Science Fundation of China (NSFC, Grant No. 11304208) and the Science and Technology Fund Projects of Shihezi University (no. 2014ZRKXJQ03).

References

1. H. Kroto, R. E. Smalley and J. Heath, Nature, 1985, 318, 162–163.
2. T. Guo, C. Jin and R. E. Smalley, J. Phys. Chem., 1991, 95, 4948–4950.
3. F. Jensen and H. Toftlund, Chem. Phys. Lett., 1993, 201, 89–96.
4. D. L. Strout, J. Phys. Chem. A, 2000, 104, 3364–3366.
5. H. Wu, X. Xu, H. Jiao, F. Zhang and J. Jia, Chin. Sci. Bull., 2003, 48, 1102.
6. T. Oku, A. Nishiwaki and I. Narita, Sci. Technol. Adv. Mater., 2004, 5, 635–638.
7. M. D. Esrafili and R. Nurazar, Superlattices Microstruct., 2014, 67, 54–60.
8. T. Oku, M. Kuno and I. Narita, J. Phys. Chem. Solids, 2004, 65, 549–552.
9. M. D. Esrafili and R. Nurazar, Comput. Mater. Sci., 2014, 92, 172–177.
10. T. Oku, Energies, 2015, 8, 319–337.
11. A. Soltania, M. T. Baei, E. T. Lemeski and M. Shahini, Superlattices Microstruct., 2014, 76, 315–325.
12. G. Seifert, P. W. Fowler, D. Mitchell, D. Porezag and T. Frauenheim, Chem. Phys. Lett., 1997, 268, 352–358.
13. W. H. Moon, M. S. Son and H. J. Hwang, Appl. Surf. Sci., 2007, 253, 7078–7081.
14. T. Oku, T. Hirano, M. Kuno, T. Kusunose, K. Niihara and K. Suganuma, Mater. Sci. Eng., B, 2000, 74, 206–217.
15. H. Wu, X. Fan and J. Kuo, Int. J. Hydrogen Energy, 2012, 37, 14336–14342.
16. H. Wu, X. Fan, J. Kuo and W. Deng, Chem. Commun., 2010, 46, 883–885.
17. G. J. Hutchings and D. T. Grady, Appl. Catal., 1985, 16, 411–415.
18. G. J. Hutchings and D. T. Grady, Appl. Catal., 1985, 17, 155–160.
19. G. J. Hutchings, J. Catal., 1985, 96, 292–295.
20. B. Nkosi, N. J. Coville and G. J. Hutchings, J. Chem. Soc., Chem. Commun., 1988, 71–72.
21. X. Wei, F. Wei, W. Qian, G. Luo, H. Shi and Y. Jin, Chin. J. Process Eng., 2008, 6, 034.
22. Q. Song, S. Wang, B. Shen and J. Zhao, Pet. Sci. Technol., 2010, 28, 1825–1833.
23. U. Dzhemilev, O. Vostrikova and G. Tolstikov, AE Shilov, Gordon and Breach, New York, 1986, vol. 2.
24. S. A. Mitchenko, E. V. Khomutov, A. A. Shubin and Y. M. Shul'ga, J. Mol. Catal. A: Chem., 2004, 212, 345–352.
25. B. Nkosi, M. D. Adams, N. J. Coville and G. J. Hutchings, J. Catal., 1991, 128, 378–386.
26. J. Zhang, Z. He, W. Li and Y. Han, RSC Adv., 2012, 2, 4814–4821.
27. X. Li, M. Zhu and B. Dai, Appl. Catal., B, 2013, 142–143, 234–240.
28. C. Huang, M. Zhu, L. Kang and B. Dai, Catal. Commun., 2014, 54, 61–65.
29. C. Huang, M. Zhu, L. Kang, X. Li and B. Dai, Chem. Eng. J., 2014, 242, 69–75.
30. M. Zhu, L. Kang, Y. Su, S. Zhang and B. Dai, Can. J. Chem., 2013, 91, 120–125.
31. M. Conte, A. F. Carley, C. Heirene, D. J. Willock, P. Johnston, A. A. Herzing, C. J. Kiely and G. J. Hutchings, J. Catal., 2007, 250, 231–239.
32. K. Zhou, W. Wang, Z. Zhao, G. Luo, J. T. Miller, M. S. Wong and F. Wei, ACS Catal., 2014, 4, 3112–3116.
33. M. Conte, A. F. Carley, G. Attard, A. A. Herzing, C. J. Kiely and G. J. Hutchings, J. Catal., 2008, 257, 190–198.
34. J. Ma, S. Wang and B. Shen, React. Kinet., Mech. Catal., 2013, 110, 177–186.
35. S. Wang, B. Shen and Q. Song, Catal. Lett., 2009, 134, 102–109.
36. J. Zhao, X. Cheng, L. Wang, R. Ren, J. Zeng, H. Yang and B. Shen, Catal. Lett., 2014, 144, 2191–2197.
37. J. Zhao, J. Zeng, X. Cheng, L. Wang, H. Yang and B. Shen, RSC Adv., 2015, 5, 16727–16734.
38. K. Zhou, J. Jia, C. Li, H. Xu, J. Zhou, G. Luo and F. Wei, Green Chem., 2015, 17, 356–364.
39. X. Li, Y. Wang, L. Kang, M. Zhu and B. Dai, J. Catal., 2014, 311, 288–294.
40. B. Dai, K. Chen, Y. Wang, L. Kang and M. Zhu, ACS Catal., 2015, 5, 2541–2547.
41. X. Wang, B. Dai, Y. Wang and F. Yu, ChemCatChem, 2014, 6, 2339–2344.
42. K. Zhou, B. Li, Q. Zhang, J. Q. Huang, G. L. Tian, J. C. Jia, M. Q. Zhao, G. H. Luo, D. S. Su and F. Wei, ChemSusChem, 2014, 7, 723–728.
43. K. Zhou, J. Si, J. Jia, J. Huang, J. Zhou, G. Luo and F. Wei, RSC Adv., 2014, 4, 7766–7769.
44. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, H. P. H. X. Li, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian Inc., Wallingford CT, 2010.
45. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
46. C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154–2161.
47. C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527.
48. F. B. van Duijneveldt, J. G. van Duijneveldt-van de Rijdt and J. H. van Lenthe, Chem. Rev., 1994, 94, 1873–1885.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra08266h

---