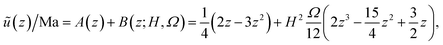DOI:
10.1039/C5RA08207B
(Paper)
RSC Adv., 2015,
5, 48563-48568
Maze solving using temperature-induced Marangoni flow
Received
4th May 2015
, Accepted 22nd May 2015
First published on 22nd May 2015
Abstract
The pH-induced Marangoni flow has been recently shown to be of use for analog computing of topological problems, such as maze solving. Here we show that the temperature-induced Marangoni flow can also be used to find the shortest path in a maze filled with a hot solution of a fatty acid, where the temperature gradient is created by cooling down the exit of the maze. Our method utilizes the fact that the temperature-induced Marangoni flow can transport dye particles at the liquid–air interface added to the entrance of the maze which subsequently dissolve in water during their motion revealing the most likely paths. The most intense flow is maintained through the shortest path which is, therefore, marked by the most intense color of the dissolved dye particles.
1. Introduction
So-called “unconventional computing” offers alternative approaches to solving some NP-hard mathematical problems in ways which are distinctly different in nature to those exploiting the established Von Neumann computer architecture.1 Unconventional chemical computing provides methods and algorithms in which chemistry plays a key role in driving phenomena which leads to the desired solution.2 In this new framework, there are generally two strategies which can be followed. One relies on designing and building logic (AND, OR, NAND, NOR and INV) gates, and combining these building blocks into an “unconventional” computational device.3–7 The second strategy is quite different and global in nature and involves using a physical or chemical phenomenon instead of relying on an assembly of local computational units (logical gates).2,8–10 In the latter case the solution is derived by exploiting a physical phenomenon that drives the “computation”, for example the soap bubble computers.11 The analog nature of this approach has the potential to make it more robust in many practical situations due to the reliance on readily used in electric instrument technology which precedes the digital computing. In the last few decades several analogue computational techniques have been explored and used for maze solving, including finding the shortest path.12–29 These methods can be grouped as physical-, biological-, electronic- and chemical, depending on the phenomena utilized in obtaining the solution. Examples relevant for maze solving include applying a pressure difference in a channel network,15 glow discharge in a microfluidic chip14,27 or reconfiguration of an organism (slime mold) between two food sources within the maze.13,19 Other successful approaches to “analog” maze solving have also been presented based on artificial chemotaxis in a liquid phase induced by the gradient of either pH or salt concentration.16,23,26 Recently, we showed that a pH-induced Marangoni flow in a millimeter sized channel network filled with an alkaline solution of a fatty acid provides a method for identifying the shortest path and, importantly, all existing paths through a maze in a parallel fashion.23 The Marangoni flow is established and maintained by the surface tension gradient at the liquid–air interface induced by pH. The resulting flow then drags chemically passive particles (dye powder particles) towards the exit of the maze following the shortest path. Marangoni flows are not limited to liquid–air interfaces; a successful realization of maze solving in a microfluidic maze has been presented using a submerged gel particle in a bulk liquid driven by the liquid-mixing-induced Marangoni effect.21
The aforementioned methods for non-conventional maze solving are all based on the presence of a gradient of a thermodynamical potential and thus confirm the universality of the principle. It is thus suggested that a gradient of any thermodynamic potential could be employed for this purpose. In our studies we found that, in addition to the hitherto known examples, also a temperature gradient can induce a Marangoni flow which can be used to solve the maze problem. Importantly, temperature gradients can be generated very easily with Peltier technology, and thus the results presented below may be of importance for future technological applications of Marangoni flow based analog computing.
2. Experimental
In experiments, we filled a centimeter-sized maze (channel depth of 1 mm and channel width of 1.4 mm) with a hot aqueous solution of sodium hydroxide (Sigma-Aldrich) with the concentration of 0.05 M that contained 0.2 v% of 2-hexyldecanoic acid (Sigma-Aldrich). Temperature of this solution was set to 373 K prior to transferring it (∼250 μL) to maze that were designed by photo- and laser-lithography and made of polydimethylsiloxane (PDMS). In order to create a temperature gradient in the maze, a small stainless steel sphere (d = 4 mm and m = 0.435 g) was cooled down using dry ice, and it was placed at one entrance (exit) of the maze prior to experiments. Immediately after the addition of the cooled metallic sphere, a small amount of phenol red dye (Sigma-Aldrich) powder (∼0.3 mg) was placed at the liquid–air interface at the other entrance of the maze (starting point). Maze solving was monitored by an optical image processing system. Fig. 1 shows the experimental setup.
 |
| | Fig. 1 The sketch of the experimental setup. | |
3. Results and discussion
3.1 Experimental findings
Positioning of a cooled (cold) metallic sphere in the hot solution lowers the temperature in the proximity of the sphere and creates a temperature gradient through the channel network in the maze. This temperature gradient translates into a surface tension gradient at the liquid–air interface, which induces a fluid flow, the so-called the Marangoni flow.30 Thus dye particles located at the liquid–air interface are dragged by this flow and move passively and collectively towards the lower temperature region. During the transport, the dye particles dissolve in water phase, colorize it and visualize the shortest path. Fig. 2 presents this maze solving method using temperature-induced liquid flow. The shortest path is found and visualized within ∼20 s.
 |
| | Fig. 2 Maze solving and finding the shortest paths in a maze filled with a hot alkaline solution of 2-hexyldecanoic acid at different times (a) t = 5 s, (b) t = 10 s, (c) t = 15 s and (d) t = 20 s. A cooled metallic sphere is placed at the exit (bottom). Phenol red dye particles are added at the entrance of the maze (top-right corner). Marangoni flow induced by temperature gradient carries particles towards the low temperature (higher surface tension) region at the liquid–air interface, and the shortest path is explored and visualized due to water solubility of the dye. | |
The Marangoni flow at the interface is always oriented towards the higher surface tension regions. The surface tension of a liquid is inversely proportional to temperature deviation from the critical temperature, so the lower the temperature is, the higher the surface tension is. Consequently, the flow at the liquid–air interface is directed from the region of higher temperature to the region of lower temperature (Fig. 3). This simple physical phenomenon can be utilized for efficient maze solving. The most intense fluid flow is established along the shortest path in a maze, where the gradient of the surface tension at the liquid–air interface is the highest, thus the majority of dye particles move toward the exit on the shortest path. It should be noted that we tried several fatty acids (such as oleic acid) at various concentrations and pH (ranging from 1 to 12), but among those tested, the most intense fluid flow can be established in case of 2-hexyldecanoic acid in highly basic solution. Therefore, we used this experimental condition for maze solving as described in the Experimental section.
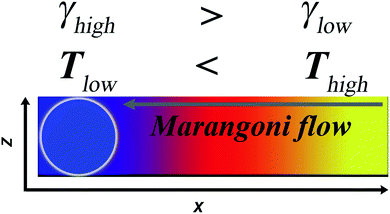 |
| | Fig. 3 The mechanism of the maze solving: temperature induced Marangoni flow. | |
In order to illustrate the maze solving dynamics we measured the dependence of the surface tension of fatty acid solution on temperature using the pendant drop method. Increasing the temperature decreases the surface tension (γ) virtually linearly, γ ∝ k(Tc − T), where k and Tc are the Eötvös constant and critical temperature, respectively. We used a boiling solution to fill the maze. A potential complication stems from the unavoidable decrease of the temperature of the solution in narrow channels in the maze. We measured this temperature drop, and the temperature decreased typically to 333 K prior to starting the experiments (placing dye powder particles to the entrance). The addition of the metallic sphere cooled down with dry ice warrants that the temperature at the exit is 273 K at the beginning of the experiments. Consequently, the temperature difference between the exit and the starting point is 60 K, which translates into 20.0 mN m−1 surface tension difference obtained from the pendant drop shape analysis (i.e., it is twice as large as the surface tension difference in the case of pure water). A pendant drop's shape depends on its surface tension and gravity. The degree of variation from the spherical shape was monitored with a camera at temperatures between 283 and 333 K with 5 K steps. From the video images the surface tensions were calculated using the Young–Laplace equation. Surface tension gradient in our experiments is 470 mN m−2, which is estimated from the surface tension difference and the length of the shortest path, which is 4.25 cm measured from Fig. 2. This surface tension gradient drives the flow at the liquid–air interface towards higher surface tension region (lower temperature).
There are two important empirical and experimental issues that should be mentioned and discussed. First, in the case of fluid flows induced by a temperature gradient, the average velocity of the liquid at the liquid–air interface is smaller than that in pH gradient-induced flow. In other words, the temperature-induced Marangoni effect is relatively weak and can, therefore, be used to solve topologically simple mazes, where the length of the shortest path is reduced compared to pH-driven cases.23 This is attributed to the fact that pH can change the surface tension of the solution of fatty acid in a more pronounced way than the temperature can.31 Another effect that needs to be taken into account arises from the fact that a horizontal temperature gradient between the entrance and the exit of the maze induces the Rayleigh–Bénard convection32 (near the cooled down metallic sphere the fluid moves downwards and continues its motion at the bottom of the channel towards the region of higher temperature, and due to inertia the fluid moves in opposite direction near the liquid–air interface, i.e., towards the lower temperature region). In effect, the flow responsible for maze solving is driven, in general, by both the Marangoni flow and the Rayleigh–Bénard convective cell established in the maze. We show below that the Rayleigh–Bénard convection is insignificant for sufficiently thin fluid layers.
3.2 Theoretical investigation
In order to estimate the importance of the two contributions driving the flow in the maze, we consider the simplest configuration in which a fluid flow is induced by a horizontal temperature gradient. We consider a situation when a horizontal fluid layer with a free surface is contained within a rigid container with the horizontal temperature gradient induced by imposing a constant temperature difference on two opposite walls. In order to capture the essential features of the dynamics we focus on the flow far away from the rigid boundaries and consider the contributions from the convective motions due to buoyancy and the surface-driven flow component due to Marangoni stresses arising due to the horizontal temperature difference. A significant difference between this setup and the classical problem with the vertical temperature gradient is that the unperturbed/reference fluid flow is non-trivial (i.e., there is no zero-velocity solutions even in the absence of perturbations). In what follows we only focus on determining the relative importance of the buoyancy versus Marangoni driven components in the unperturbed reference state in shallow fluid layers and do not consider potential instabilities of the reference flow which might arise in sufficiently deep layers with sufficiently strong temperature gradients.
We consider a horizontal layer of a thermally conductive fluid with density ρ under the Boussinesq approximation with the governing equations given by
| |
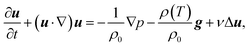 | (1) |
| |
 | (3) |
where
u(
x,
t),
T(
x,
t) are the velocity and temperature fields,
p(
x,
t) denotes the pressure field,
g is the acceleration of gravity,
ν is the kinematic viscosity, and
κ is the thermal diffusivity. The system is heated with a constant temperature gradient
β imposed in the horizontal direction and the free surface is assumed horizontal and non-deformable. Consequently the temperature distribution on the bottom is given by
T(
x,
y,
z = 0,
t) =
T0 +
βx, where
T0 is the temperature of the “cold” wall. The fluid density under the Bousinessq approximation is given by the linear equation of state
ρ(
x,
t) =
ρ0(1 −
α(
T(
x,
t) −
T0)) with
α the coefficient of thermal expansion and
ρ0 the reference density at
T0. The temperature-dependent surface tension is given by
γ(
x,
t) =
γ0 −
σ(
T(
x,
t) −
T0), where

is a positive constant.
The eqn (1)–(3) can be non-dimensionalised by using the depth H of the fluid as the length scale, H2/κ for the time scale, ρ0νκ/H2 for pressure and βH for temperature. This leads to equations
| |
 | (4) |
| |
 | (6) |
with boundary conditions.
| | |
u|z=0 = 0, (∂zu + Ma∇x,yT)|z=1 = 0, T|z=0 = T0 + x,
| (7) |
where Pr =
ν/
κ is the Prandtl number, Ra =
αβH4g/(
νκ) is the Rayleigh number, Ma =
αβH2/(
ρ0νκ) is the Marangoni number, and
C = 1/(
αβH).
In the presence of the horizontal temperature gradient the steady flow, representing the basic flow state, is given by
| | |
Pr−1(u·∇)u=−∇p − Ra(C − (T − T0))ez + Δu,
| (8) |
with the same boundary conditions as above.
We look for the steady solutions far away from the boundaries in the form
| |
u = (ũ(z),0,0)T, T(z) = T0 + x + ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) (z). (z).
| (11) |
Substituting these into eqn (8)–(10) and eliminating the pressure leads to
| |
 | (12) |
| |
 | (13) |
with boundary conditions
| |
ũ(z = 0) = 0, ∂zũ|z=1 = −Ma, ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) (z = 0) = 0, (z = 0) = 0,
| (14) |
with the constraint due to the incompressibility in
(9) given by
| |
 | (15) |
The solutions to (12) satisfying the constraints in eqn (14) and (15) are obtained easily in the form
| |
 | (16) |
and the solutions of
(13) are given by
| |
 | (17) |
Note that there remains one free constant of integration in the solution for ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) (z). This is due to the need for an additional boundary condition for
(z). This is due to the need for an additional boundary condition for ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) (z) on the free surface (i.e., at z = 1).
(z) on the free surface (i.e., at z = 1).
3.3 Competition between the buoyancy driven and Marangoni components in the steady solutions
It is transparent, based on the steady solutions (16) and (17), that (i) there has to be a nontrivial fluid flow in the presence of a horizontal temperature gradient, and (ii) both the buoyancy driven effect and thermocapillary effect sustain the flow. Here, we illustrate the relative importance of these two effects on the flow in (16) as a function of the fluid depth H. In order to achieve a meaningful comparison, we note that Ra ∝ H4, Ma ∝ H2 and rewrite (15) by factoring out the dependence on H in the dimensionless numbers Ra and Ma| |
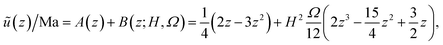 | (18) |
where A and B represent the Marangoni and buoyancy driven components, respectively, and Ω = αρ0g/σ. Therefore, for all other parameters constant, the Marangoni effects dominate the flow for sufficiently thin fluid layer. We show the profiles of the horizontal velocity (18) for different values of H in Fig. 4. Fig. 5 shows the two components of the flow (18) independently as a function of the fluid depth H. In the notation of (18) the Marangoni driven component is independent of H and shown in black; the buoyancy driven flow components are plotted in dashed lines for different values of H. Clearly, the importance of the buoyancy driven flow component quickly diminishes with decreasing fluid depth.
 |
| | Fig. 4 Horizontal velocity profiles for the steady solution (eqn (18)) of the flow driven by the horizontal velocity gradient as a function of the fluid depth H (the plots show ũ(z)/Ma for Ω = 6.2 × 103 m−2. The value of omega was calculated based on experimental parameters of the system). | |
 |
| | Fig. 5 The thermocapillary (A(z)) and buoyancy driven (B(z;H,Ω)) terms of the horizontal velocity profiles for the steady solution (eqn (18)) of the flow driven by the horizontal velocity gradient as a function of the fluid depth H (the plots show curves for Ω = 6.2 × 103 m−2. The value of omega was calculated based on experimental parameters of the system). | |
4. Conclusions
We presented a simple method for maze solving using the thermocapillary effect. We used a temperature gradient to drive the fluid flow, which is maintained by the non-uniform distribution of the surface tension (gradient of surface tension) at the liquid–air interface. Induced flow can drag passive tracers such as small dye particles, which dissolve in water phase thus visualizing the shortest path.
It should be noted that the gradient of the surface tension to propel particles has been used in several cases.33–35 Even the camphor boats represent similar system.36,37 In these systems, the motion of particles is governed by a local gradient of the surface tension created by a chemical entity (e.g., polymer gel, camphor particles) emitting surface active substances, thus changing locally the surface tension near the chemical object at the liquid–air interface. This is in contrast to our system, in which the surface tension gradient is established globally (independently of tracer particles) and exists through the maze. In the formerly mentioned systems the velocity of the particles depends on the shape and size of the particles, and it can reach an order of 10 cm s−1, this value is greater that the velocities of passive tracer particles measured in globally induced Marangoni flows (0.1–1 cm s−1). In other words, in our system the particles do not contribute for their motion and for the generation of the globally existing Marangoni flow. An extension of our method would be using topographically controlled Bénard–Marangoni cells for maze solving, in which the motion of particles could be externally driven.38
Additionally, we showed by simple theoretical calculations that in our setup (where the depth of the channel is negligible compared to its length), and provided that Ra ≪ Ma, the driving phenomenon for mass transfer is the thermocapillary effect. In this way, we provided an additional unconventional computing method for maze solving.
Acknowledgements
Authors acknowledge the financial support of the Hungarian Research Fund (OTKA K104666). A. B. is grateful for financial support from the Swiss National Science Foundation project no. #200021-137868. R. T. is grateful for financial support from the Swiss National Science Foundation Marie Heim Vögtlin Fellowship no. PMPDP2-139689/1. We thank Tina Künniger at Empa for the surface tension measurements.
References
- G. D. Crnkovic and R. Giovagnoli, Entropy, 2012, 14, 2408 CrossRef PubMed.
- A. Adamatzky, B. De Lacy Costello and T. Asai, Reaction-Diffusion Computers, Elsevier, 2005 Search PubMed.
- A. Tóth and K. Showalter, J. Chem. Phys., 1995, 103, 2058 CrossRef PubMed.
- A. Adamatzky and B. D. L. Costello, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 046112 CrossRef.
- J. N. Górecka, J. Górecki and Y. Igarashi, J. Phys. Chem. A, 2007, 111, 885 CrossRef PubMed.
- A. P. de Silva and N. D. McClenaghan, J. Am. Chem. Soc., 2000, 122, 3965 CrossRef CAS.
- G. Strack, M. Ornatska, M. Pita and E. Katz, J. Am. Chem. Soc., 2008, 130, 4234 CrossRef CAS PubMed.
- A. Adamatzky, Chaos, Solitons Fractals, 2004, 21, 1259 CrossRef CAS PubMed.
- A. Adamatzky, Phys. Lett. A, 2009, 374, 264 CrossRef CAS PubMed.
- A. Adamatzky, Int. J. Gen. Syst., 2015, 44, 277 CrossRef PubMed.
- M. Bern and R. Graham, Sci. Am., 1989, 260, 84 CrossRef.
- O. Steinbock, A. Tóth and K. Showalter, Science, 1995, 267, 868 CrossRef CAS PubMed.
- T. Nakagaki, H. Yamada and A. Tóth, Nature, 2000, 407, 470 CrossRef CAS PubMed.
- D. R. Reyes, M. M. Ghanem, G. M. Whitesides and A. Manz, Lab Chip, 2002, 2, 113 RSC.
- M. J. Fuerstman, P. Deschatelets, R. Kane, A. Schwartz, P. J. A. Kenis, J. M. Deutch and G. M. Whitesides, Langmuir, 2003, 19, 4714 CrossRef CAS.
- I. Lagzi, S. Soh, P. J. Wesson, K. P. Browne and B. A. Grzybowski, J. Am. Chem. Soc., 2010, 132, 1198 CrossRef CAS PubMed.
- A. M. Reynolds, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 062901 CrossRef CAS.
- Y. V. Pershin and M. Di Ventra, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 046703 CrossRef.
- A. Adamatzky, IEEE Trans. NanoBiosci., 2012, 11, 131 CrossRef PubMed.
- C. Scherber, A. J. Aranyosi, B. Kulemann, S. P. Thayer, M. Toner, O. Iliopoulosc and D. Irimia, Integr. Biol., 2012, 4, 259 RSC.
- Y. Wang, X. Liu, X. Li, J. Wu, Y. Long, N. Zhao and J. Xu, Langmuir, 2012, 28, 11276 CrossRef CAS PubMed.
- K. Suzuno and D. Ueyama, Proceedings of the 19th Symposium on Simulation of Traffic Flow, 2013, p. 85 Search PubMed.
- K. Suzuno, D. Ueyama, M. Branicki, R. Tóth, A. Braun and I. Lagzi, Langmuir, 2014, 30, 9251 CrossRef CAS PubMed.
- H. Wang, X. Lu, X. Zhang, Q. Wang and Y. Deng, Sci. World J., 2014, 2014, 271280 Search PubMed.
- S. Ayrinhac, Phys. Educ., 2014, 49, 443 CrossRef.
- J. Cejkova, M. Novak, F. Stepanek and M. Hanczyc, Langmuir, 2014, 30, 11937 CrossRef CAS PubMed.
- A. E. Dubinov, A. N. Maksimov, M. S. Mironenko, N. A. Pylayev and V. D. Selemir, Phys. Plasmas, 2014, 21, 093503 CrossRef PubMed.
- G. Zhao and M. Pumera, Lab Chip, 2014, 14, 2818 RSC.
- A. Braun, R. Tóth and I. Lagzi, Nachr. Chem., 2015, 63, 445 CrossRef CAS PubMed.
- L. E. Scriven and C. V. Sternling, Nature, 1960, 167, 186 CrossRef PubMed.
- N. M. Kovalchuk and D. Vollhardt, Langmuir, 2010, 26, 14624 CrossRef CAS PubMed.
- A. V. Getling, Rayleigh–Benard convection: structures and dynamics, World Scientific, 1998 Search PubMed.
- J. P. Gong, S. Matsumoto, M. Uchida, N. Isogai and Y. Osada, J. Phys. Chem., 1996, 100, 11092 CrossRef CAS.
- N. Bassik, B. T. Abebe and D. H. Gracias, Langmuir, 2008, 24, 12158 CrossRef CAS PubMed.
- G. Zhao and M. Pumera, Chem.–Asian J., 2012, 7, 1994 CrossRef CAS PubMed.
- S. Nakata, Y. Doi and H. Kitahata, J. Colloid Interface Sci., 2004, 279, 503 CrossRef CAS PubMed.
- E. Heisler, N. J. Suematsu, A. Awazu and H. Nishimori, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 055201(R) CrossRef.
- R. F. Ismagilov, D. Rosmarin, D. H. Gracias, A. D. Stroock and G. M. Whitesides, Appl. Phys. Lett., 2001, 79, 439 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2015 |
Click here to see how this site uses Cookies. View our privacy policy here.  c,
Kohta Suzunod,
Daishin Ueyamad and
István Lagzi*a
c,
Kohta Suzunod,
Daishin Ueyamad and
István Lagzi*a
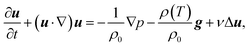

 is a positive constant.
is a positive constant.


![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) (z).
(z).


![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) (z = 0) = 0,
(z = 0) = 0,



![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) (z). This is due to the need for an additional boundary condition for
(z). This is due to the need for an additional boundary condition for ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) (z) on the free surface (i.e., at z = 1).
(z) on the free surface (i.e., at z = 1).