Interfacial rheology and aggregation behaviour of amphiphilic CBABC-type pentablock copolymers at the air–water interface: effects of block ratio and chain length†
Zhiguang Liab,
Xiaoyan Ma*ab,
Duyang Zangac,
Xinghua Guanab,
Lin Zhuab,
Jinshu Liuab and
Fang Chenab
aKey Laboratory of Space Applied Physics and Chemistry, Ministry of Education, School of Science, Northwestern Polytechnical University, Xi’an 710129, Shaanxi province, China. E-mail: m_xiao_yana@nwpu.edu.cn
bKey Laboratory of Polymer Science and Technology, School of Science, Northwestern Polytechnical University, Xi’an 710129, Shaanxi province, China
cNPU-UM II Joint Lab of Soft Matter, School of Science, Northwestern Polytechnical University, Xi’an 710129, China
First published on 18th September 2015
Abstract
The interfacial rheology and aggregation behaviour of three amphiphilic CBABC-type pentablock copolymers possessing different block ratios and chain lengths were investigated at the air–water interface, in which C, B and A represent poly(trifluoroethyl methacrylate)/PTFEMA, poly(methyl methacrylate)/PMMA and poly(ethylene glycol)/PEG, respectively. The influence of the block ratio and chain length on the interfacial rheology of the Langmuir films was studied via continuous compression, successive addition and step compression methods. The surface pressure–mean molecular area isotherms and limiting mean molecular areas of the three copolymers were studied via continuous compression. The surface pressure and modulus obtained from the continuous compression and successive addition methods were compared. Furthermore, the relaxation of the monolayer was discussed using the step compression method. A relaxation process was proposed that related to the adsorption–desorption exchange of molecules and polymer segments on the surface (fast relaxation process) and the reconformation of the adsorbed macromolecules inside the adsorption layer (slow relaxation process) at different mean molecular areas of compression. In addition, the Langmuir–Blodgett (LB) films prepared at various surface pressures from the three copolymers were scanned using atomic force microscopy (AFM) images, and a variety of morphologies such as macroporous, rugged, reticular and discontinuous continent structures were observed. Finally, the packing model of the structure evolution for the pentablock copolymer aggregates at the air–water interface was proposed.
1. Introduction
Amphiphilic block copolymers with complex architectures, and different block ratios and chain lengths have attracted considerable attention due to their outstanding solution properties, such as their self-assembly in the presence of a selective solvent or surface.1–3 In particular, the current interest in the properties of interfacial layers formed by these copolymers stems from their ability to spontaneously organize into ordered surface patterns.Many amphiphilic copolymers tend to form an ordered monolayer with a precise thickness and an organized molecular assembly with a well-defined molecular orientation when spread at the air–water interface.4–8 The surface morphologies of the monolayer can be easily adjusted by a lot of controllable factors, including the chemical structure of the copolymers as well as the relative length of each block, surface pressure, molecular weight, and so on.1,7,9–12 Through a Langmuir film balance, we can obtain information about not only the mechanical properties and the interaction of the molecules, but also the size, shape and orientation of the molecules.7,13 Duran et al. and Moffitt’s group found that the surface morphologies of the copolymer depended on the relative amounts of hydrophobic and hydrophilic blocks of polystyrene-b-poly(ethylene oxide) (PS-b-PEO) in both linear and star systems.14–17 The ability of the PS to aggregate into the surface morphologies was impacted by the ability of PEO to separate the PS chains, and these tendencies directly related to the block ratio and chain length.18 Furthermore, Logan and co-workers5 investigated the influence of PS on the morphologies of the monolayers by examining a series of PS-b-PEO containing unchanging PEO and variable chain lengths of PS, and found that the different morphologies of the copolymers formed were exclusively dot, spaghetti and continent nanostructures. In addition, the surface pressure at which a film was transferred led to apparent changes in the aggregation in star PS-b-PEO systems.
The surface properties of the amphiphilic block copolymers have been widely studied using the Langmuir trough technique, which allows the control of the nanostructures formed at the air–water interface.19–23 The two-dimensional properties of the aggregates and the conformational changes of the copolymer chains induced by compression of the film can be derived from interfacial rheology.24–27 Interfacial rheology of a Langmuir film is determined by a number of parameters, such as the spreading concentration, compression rate, block ratio and chain length.16,17,28–33 Furthermore, the investigation of interfacial rheology is used for understanding the viscoelastic properties,34 which provide the modulus and relaxation behaviour.35 Langevin et al.36 investigated the compression modulus of acrylic Langmuir films, which related to the elastic energy stored by the surface layer upon compression. Relaxation reveals a nonequilibrium via step compression, and could obtain the dilational modulus. Our group6 revealed the relaxation behaviour of the polystyrene-b-poly(acrylic acid) (PS-b-PAA) block copolymer. The modulus and two relaxation times of the monolayer were obtained from the fit of the relaxation isotherms. In particular, two types of relaxation mechanisms were involved for the two relaxation times, one was the exchange of molecules between the polymer solution and the interface, the other was the conformational change of molecules in the interfacial layer.37
In recent years, numerous investigations have been carried out on poly(ethylene glycol) (PEG) based block copolymers at the air–water interface.4,5,38–41 The surface-active nature of PEG promotes its spontaneous adsorption at the air–water interface and causes it to become more easily dissolved in the aqueous subphase. The hydrophobic block of poly(trifluoroethyl methacrylate) (PTFEMA) with its advantages of hydrophobicity, low surface energy and good stability is the best candidate to tether PEG to the surface. To the best of our knowledge, very little work has been carried out looking into fundamentally understanding the interfacial rheology and aggregation behaviour of PTFEMA based block copolymers at the air–water interface. Therefore, fundamental studies of PTFEMA based block copolymers performed at the interface can provide valuable interfacial phase behaviour in order to further guide their applications. In addition, the equilibrium behaviour of the PMMA based block copolymer films has been studied extensively in recent decades.2,42–48 And as far as we know, most of the investigations carried out at the air–water interface have paid more attention to AB-type diblock copolymers, while only a few studies have examined the aggregation of ABA-type multiblock copolymers,4,7,49 and the treatment of multiblock copolymers to adequately predict the aggregation and the interfacial rheology is still missing.
In order to reveal the self-assembly of PTFEMA based multiblock copolymers at the air–water interface, the interfacial rheology and aggregation behaviour of three amphiphilic CBABC-type pentablock copolymers of PTFEMA-b-PMMA-b-PEG-b-PMMA-b-PTFEMA with different block ratios and chain lengths are investigated. The aim of this study is to determine the precise influence of the block ratio and chain length on the interfacial rheology. The isotherms of the surface pressure and modulus via the compression and successive addition methods are compared. The relaxation times and dilational moduli in the relaxation are discussed through step compression method. Moreover, the morphologies of LB films prepared from the three copolymers at various surface pressures are also characterized. Finally, the packing model of the pentablock copolymer aggregate at the air–water interface is proposed.
2. Experimental
2.1. Materials
Three pentablock copolymers of PTFEMA-b-PMMA-b-PEG2000-b-PMMA-b-PTFEMA with different molecular weights were synthesized via atom transfer radical polymerization in our previous study.50 Gel permeation chromatography (GPC) analysis results are listed in Table 1. Water used in all experiments was de-ionized and ultrafiltrated to 18.2 MΩ with an ELGA Lab water system. Chloroform (CHCl3) was analytically pure and used without further purification. The spreading concentrations were prepared by weighing an appropriate amount of the copolymer into new glass reagent vials cleaned three times with acetone in an ultrasonic cleaning tank, and then a certain amount of CHCl3 was added gravimetrically; all the solutions were prepared 6 h prior to use to allow for equilibration.| Serial number | Block ratio PEG![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PMMA PMMA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PTFEMA PTFEMA |
Mn, g mol−1 | PDI |
|---|---|---|---|
| Copolymer-1 | 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 15 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 790 790 |
1.49 |
| Copolymer-2 | 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11 11 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 340 340 |
1.58 |
| Copolymer-3 | 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 7 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
1.57 |
2.2. Langmuir trough, isotherms of Langmuir films, BAM and AFM images
Isotherm characterization was accomplished using a Teflon Langmuir trough system (W = 200 mm, L = 310 mm, JML04C3, Powereach Ltd., China) equipped with two moving barriers and a Wilhelmy plate. The isotherms were measured with symmetric compression at a rate of 5 mm min−1 at 20 ± 2 °C.Three pentablock copolymers were spread at the air–water interface. In these experiments, the concentration of the solution was 0.3 mg mL−1, and the total mass of the copolymers was kept constant (0.015 mg).
To prepare a Langmuir film (normally an insoluble molecular film at the air–water interface), the three pentablock copolymers dissolved in CHCl3 were spread dropwise on an ultra-pure water subphase using a microsyringe, and the solvent was allowed to evaporate completely for 30 min. The surface concentrations were varied either by compressing the barriers or by adding small aliquots of solution to the interface (successive addition).36,51,52 Each small aliquot of solution was spread in successive addition and evaporated for 5 min. The relaxation was studied via step compression where the surface film was firstly compressed and afterwards the barriers were stopped to allow the relaxation of the monolayer. The relaxation curve was accepted only if the initial and final values of the surface pressure were in agreement with the corresponding equilibrium values.53
The Langmuir trough was also equipped with a Brewster Angle Microscope (JB04, Powereach Ltd., China) to image the copolymer and its solution films at the interface.
The LB films of the copolymers were the deposited films transferred onto glass substrates at various surface pressures. The glass substrate was immerged into the water subphase before spreading the copolymer solution. After being kept at the target transfer pressure, the submerged substrate was lifted vertically through the film at a speed of 3 mm min−1. These transferred films were dried in a vacuum desiccator for 24 h at room temperature. The transferred LB films were scanned in the tapping mode with AFM (MFP-3D-SA, Asylum Research Inc., USA) using silicon probes (AMCL-AC240, Olympus, Japan).
3. Results and discussion
3.1. Surface pressure–mean molecular area isotherms
Surface pressure (Π)–mean molecular area (MMA) isotherms of the Langmuir films obtained from the compression of the three pentablock copolymers are depicted in Fig. 1. It is found that copolymer-1 and copolymer-2 exhibit four regions (pancake, pancake to brush transition, brush and collapse), which is similar to the results in previous research.6,54 On the other hand, the Π–MMA isotherm of copolymer-3 shows only three regions, lacking the collapse region.In the pancake region (Region A), macromolecules of the copolymer occupy a large mean molecular area on the water surface and do not contact each other.55 The compression causes only an increase in polymer density, resulting in the surface pressure close to zero.6 In this case, the PEG chains are progressively dissolved in the aqueous subphase. In Region B, lateral compression may cause the macromolecules to contact each other and lead to a slow rise in the surface pressure, implying that the interaction exists between the macromolecules of the copolymer on the water surface. The smooth PEG chains begin to stretch and mostly loop into the water, and the compression causes the extrusion of the PMMA chains.
Upon further compression to the brush region (Region C), the PTFEMA chains are strongly compressed so that the surface pressure steeply increases, which implies that a larger enhancement of the interaction may have occurred.55 At the end of the Π–MMA isotherms (Region D) for copolymer-1 and copolymer-2, the surface pressure exhibits a tendency to level off. It indicates that the monolayer may collapse owing to the over-compression of the copolymers and the formation of multilayer structures on the water surface.6,7 On the other hand, the surface pressure of copolymer-3 does not reach the collapse region and shows an increasing tendency at the end.
It is observed that the block ratio and hydrophobic chain length have a major impact on the profile of the isotherms, and with the increase of the hydrophobic/hydrophilic ratio and hydrophobic chain length, the transition of the monolayer occurs sooner.3,5 It is noteworthy that copolymer-1 has the longest hydrophobic chain length, which has the best effect on the phase transition and surface pressure. It causes the extrusion of the hydrophobic chains which are relatively incompressible at the end of the compression. On the other hand, copolymer-3 does not reach the collapse region, which may be due to it having the lowest hydrophobic/hydrophilic ratio of the three copolymers. It can reach the collapse point when more of it is spread as shown in Fig. S1.† Therefore, copolymer-3 retards the interaction of the molecules at the maximum packing density.
The limiting mean molecular areas of the pancake and brush conformations (A0,p and A0,b, respectively) could be quantified by extrapolating the tangents to the inflection points of the Π–MMA isotherms to a surface pressure of zero (Fig. 1). For the three copolymers, A0,p and A0,b are illustrated in Fig. 2.
 | ||
| Fig. 2 Plots of the pancake and brush limiting areas A0,p and A0,b of the copolymers determined from the Π–MMA isotherms. (a) Copolymer-1, (b) copolymer-2, (c) copolymer-3. | ||
As observed in Fig. 2, both the A0,p and A0,b of copolymer-1 are the highest, while the A0,p, and A0,b of copolymer-3 are the lowest. The values of A0,p and A0,b could be affected greatly by the chain length of the copolymers. Copolymer-1 with the longest chain length relatively occupies the largest surface area, hence the A0,p of copolymer-1 is the highest. In the brush region, the PEG chains are fully desorbed into the water, therefore the A0,b is mainly determined by both the chain lengths of the PMMA and PTFEMA chains and the incompressible interspaces between them. As a result, the A0,b of copolymer-1 is also the highest.
3.2. Interfacial rheology
It is convenient to derive the compression modulus (E) to investigate the interfacial rheology. The compression modulus gives information about the compactness and packing of the film,56 which accounts for the elastic energy storage in the film upon compression.2,57 The compression modulus can be calculated from the derivative of the equilibrium surface pressure with respect to the surface concentration of the copolymer Γ (the Π–Γ isotherms of the copolymers upon compression are shown in Fig. 3(a) and come from Fig. 1), as in eqn (1):58| E = Γ(∂Π/∂Γ) | (1) |
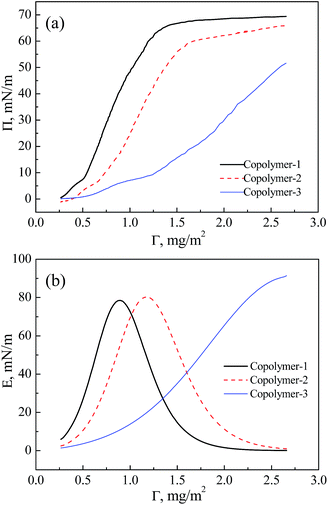 | ||
| Fig. 3 Compression properties of the three pentablock copolymers. (a) Π–Γ isotherms. (b) E–Γ isotherms. | ||
The E–Γ isotherms of the three copolymers are plotted in Fig. 3(b). It is found that the compression modulus may be correlated with the slope of the Π–Γ isotherm. Further compression is accompanied by an increase in E.59 High E is a sign that the macromolecules are packed tightly and that there is low interfacial fluidity among the packed molecules in Langmuir films. A monolayer with a high E value is rigid and difficult to deform.56 Moreover, the peak value of E represents that the molecules are in the most compact arrangement and the surface pressure increases rapidly.33 The E value decreases for copolymer-1 and copolymer-2 after the peak, which is attributed to the small value of dΠ/dΓ at higher pressure,59 indicating that no more elastic storage is possible now.60 Finally compression of the monolayer beyond the inflection point resulted in a collapse which manifested in a steep decrease of the modulus. At the end of the collapse region the modulus decreases to a low level as a consequence of the strong reduction of the available free area at the air–water interface and of the conformational degrees of freedom of the polymer chains.61,62 In this region relatively rigid monolayers fractured into straight strips. The strips piled up and formed multilayered structures as can be seen in the BAM image of copolymer-1 in the collapse region (MMA = 33.0 nm2). The BAM image is shown in Fig. S2 in the ESI.†
To further investigate the equilibrium and dynamic properties of the compression, the Π–Γ and E–Γ isotherms of successive addition are shown in Fig. 4(a) and (b), respectively. When a solution droplet is deposited on the water surface, the PEG adsorbs at the interface and the hydrophobic blocks, that are strongly incompatible with PEG and water, tend to be segregated toward the air. Subsequently, as the solvent evaporates, the copolymer “pancake” spreads over larger areas. With successive addition, the molecules gradually become closer, and the mobility of the blocks becomes restricted because of both space limitations and the mutual interactions. At the same surface concentration, the surface pressure of copolymer-1 is also the highest in Fig. 4(a).
 | ||
| Fig. 4 Equilibrium properties of the three pentablock copolymers obtained from successive addition. (a) Π–Γ isotherms and (b) E–Γ isotherms. | ||
It is obvious that the moduli for the three copolymers exhibit a maximum value. In general, successive addition can influence the surface modulus in two ways: one is to increase the surface concentration of copolymer and the other is to increase the ability of the copolymer molecules to diffuse from the bulk to the surface. The former can raise the surface pressure gradients, resulting in an increase in the modulus, and the latter may exert a contrary effect. When the concentration is low, the increase in the concentration mainly affects the surface adsorption; therefore, the modulus increases with the surface concentration. With a further increase in the surface concentration, the transfer of the copolymer molecules from the bulk to the air–water interface starts to dominate, which leads to the decrease of the modulus.63
From Fig. 3 and 4, it is found that the surface pressure and modulus in successive addition are much lower than those in compression.19,51,52 Rubio et al.53 carried out continuous compression experiments and found that once the monolayer was in the semidilute regime, the copolymer monolayer was brought into nonequilibrium states. It is more probable that continuous compression brings the system out of equilibrium, while the successive addition method reaches the equilibrium states and leads to the free arrangement of the molecules. The copolymer chains are weakly interacting, thus leading to lower values of the surface pressure and modulus. This reveals weak interactions between the molecules, thereby leading to the low stability of the films.64 Compared with successive addition, continuous compression indicates the formation of a critical concentrated solid state.
It has been reported that the surface relaxation can provide deep insight into the composition and structure of the adsorbed layers which is related to the aggregation or repulsion of the copolymer chains and the conformational rearrangement of the molecules.6,31,65 Measuring the relaxation at the air–water interface through step compression is a very useful dynamics technique to characterize the viscoelasticity of the Langmuir films.6,52,66 Fig. 5(a) shows the Π–t data of the relaxation behaviour of copolymer-1, and the variation of Π–MMA is shown in the inset of Fig. 5(a). It is found that the Π increases quickly and undergoes a sudden drop within a few seconds before tending to a new equilibrium value, illustrating that continuous compression leads to nonequilibrium states.19 This creates internal stress that acts as a restoring force for recovering the initial state when strain ceases. As a consequence, a surface pressure gradient appears and then relaxes to its equilibrium value.57 The macromolecular orientation and rearrangement at the higher surface pressure leads to a stronger internal stress, which results in a longer relaxation time.
As described in detail by Tschoegl,67 the theory of linear viscoelasticity suggests that the ΔΠ(t) relaxation transients can be described in terms of the sum of two decaying exponents and a plateau:
| ΔΠ(t) = A1e−t/τ1 + A2e−t/τ2 + ΔΠ∞ | (2) |
To further study the microscopic relaxation process and the relaxation mechanism based on the analysis above, we used an exponential function to fit the Π versus t curve obtained in the relaxation experiment. In the simplest case, when there is only one relaxation time, the pressure varies exponentially with time as e−t/τ (τ is the relaxation time).6,65 Here we choose a single exponential and two exponentials to fit the relaxation curves.
The time variation of the surface dilational modulus can be obtained from eqn (3) and (4):
| E(t) = E0e−t/τ + ΔE∞ | (3) |
| E(t) = E1e−t/τ1 + E2e−t/τ2 + ΔE∞ | (4) |
As depicted in Fig. 5(b), we found that the two exponential fitting curves fit the second and third relaxation curves better than the single exponential one. However, the first relaxation curve is better for the single exponential fitting. The main purpose of the fits is to obtain the dilational moduli and relaxation times of the copolymer films. The dilational modulus at short times can be obtained as E(0) = E1 + E2. The values of the dilational moduli and the relaxation times deduced from the fits of the Π–t evolution with eqn (3) and (4) are listed in Table 2.
| Copolymers | MMA, nm2 | E1, mN m−1 | τ1, s | E2, mN m−1 | τ2, s | F1 (%) | F2 (%) | E(0), mN m−1 | E, mN m−1 |
|---|---|---|---|---|---|---|---|---|---|
| Copolymer-1 | 108 | 0.12 | 163.90 | — | — | — | — | 0.12 | 16.04 |
| 53 | 10.98 | 30.45 | 7.67 | 496.33 | 8.07 | 91.93 | 18.65 | 76.12 | |
| 36 | 11.86 | 58.07 | 15.50 | 594.30 | 6.96 | 93.04 | 27.36 | 44.18 | |
| Copolymer-2 | 69 | 0.35 | 145.96 | — | — | — | — | 0.35 | 15.37 |
| 33 | 8.88 | 23.68 | 5.78 | 348.59 | 9.45 | 90.55 | 14.66 | 80.23 | |
| 26 | 13.53 | 82.12 | 16.30 | 1807.89 | 3.63 | 96.37 | 29.83 | 52.86 | |
| Copolymer-3 | 37 | 0.58 | 131.38 | — | — | — | — | 0.58 | 8.11 |
| 18 | 7.54 | 20.41 | 5.51 | 338.70 | 7.62 | 92.38 | 13.05 | 39.16 | |
| 13 | 10.92 | 58.80 | 13.93 | 540.83 | 7.85 | 92.15 | 24.85 | 75.66 |
As evidenced in Table 2, the times necessary for the surface pressure to reach a constant value are all quite long in different regimes. The relaxation time increased with the decreasing MMA. The good fits of the second and third relaxation curves using eqn (4) suggests that there are two physical mechanisms dominating the relaxation including fast and slow processes.68,69
The fractional contributions of the fast (F1) and slow (F2) relaxation processes can be obtained from eqn (5) and (6):70
 | (5) |
 | (6) |
The fast relaxation process with a characteristic time value (fast relaxation time τ1) of several tens of seconds is closely linked to the adsorption–desorption exchange of molecules and polymer segments on the surface.38 On the other hand, the slow relaxation process has a characteristic relaxation time value (slow relaxation time τ2) from several hundreds to thousands of seconds, and depends on the slower reconformations of the adsorbed macromolecules inside the adsorption layer.38 In Table 2 it is shown that the smaller the mean molecular area is, the longer the fast and slow relaxation times are.
In the first relaxation curve, there is only one relaxation process which can be regarded as the fast relaxation process dominating the dynamics properties. It is believed to be related to the adsorption–desorption exchange of the hydrophilic chains on the water surface. The PEG chains are found to be flat at the air–water interface before compression. With compression, the PEG chains adsorbing onto the water surface may be attributed to the rearrangement of the molecules. In the second and third relaxation curves, both the fast and slow relaxation processes influence the relaxation, and in Table 2 it is found that the slow relaxation dominates the global process.
The relaxation times are also dependent on the molecular weight and molecular architecture. In particular, copolymer-3 possesses the shortest relaxation times τ1 and τ2, which indicates the fastest adsorption–desorption exchange and a rapid molecular reorganization of the copolymer chains adsorbed at the interface probably as a result of having the lowest hydrophobicity and molecular weight.38
At the same mean molecular area, the compression modulus E and dilational modulus E(0) are compared as observed in Table 2. It is found that the compression modulus is higher than the dilational modulus. Continuous compression is a nonequilibrium and dynamic process, and the molecules do not have time to relax. Therefore, during compression the molecules aggregate more densely than in the relaxation process, and the modulus is higher in continuous compression than in step compression.
3.3. Surface morphologies of LB films
To highlight the block ratio, chain length and surface pressure dependence of the surface morphologies, the monolayer was transferred to a glass substrate from the water subphase. The submerged substrate was lifted vertically to the air, resulting in the film containing the hydrophobic chains sitting on top. Therefore, the brighter domains represent hydrophobic chains while the darker background reflects PEG or bare glass.5,6 Representative AFM images are shown in Fig. 6 and 7.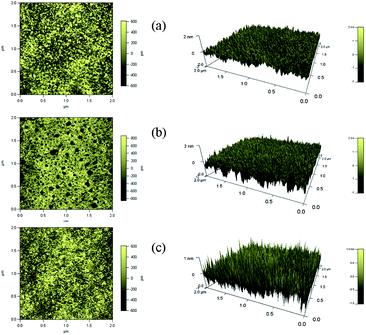 | ||
| Fig. 7 Topography (left) and 3D (right) images of the copolymer-2 LB films transferred at different surface pressures on glass substrates: (a) 5 mN m−1, (b) 30 mN m−1, (c) 62 mN m−1. | ||
As depicted in Fig. 6, the typical features are observed for the three copolymers at 30 mN m−1 in the isotherms. For copolymer-1, the images in Fig. 6(a) exhibit light raised rings surrounded by darker irregular rodlike aggregates. For copolymer-2 as depicted in Fig. 6(b), the morphology is a macroporous structure with black irregular holes. As observed in Fig. 6(c) for copolymer-3, the morphology is a rugged structure with a discontinuous continent, and darker irregular aggregates. The LB films show very large empty spaces between the domains as the chain length is decreased. Both the size and the shape of the domains seem to strongly depend on the molecular weight, block ratio and chain length,4,5 which are influenced by the chemical structure of the copolymer.
The importance of the PEG, PMMA and PTFEMA composition helps explain the nanostructures seen in the AFM images. The PEG chains are progressively dissolved in the water subphase. As a result, the morphologies of the LB films are determined by the PTFEMA and PMMA chains. A more dense continent monolayer is found in Fig. 6(a) due to the largest hydrophobic ratio and chain length of copolymer-1. The most prevalent hydrophobic block of this copolymer could thus directly produce a less extended film structure that contains the largest aggregates. With the decrease of the hydrophobic block ratio and chain length, the continuous region disappears and discontinuous continents appear (Fig. 6(b) and (c)).
In addition, the influence of the surface pressure on the assembly of the pentablock copolymers is also examined. Fig. 7 shows the typical AFM images of copolymer-2 at different surface pressures (5 mN m−1, 30 mN m−1 and 62 mN m−1).
As exhibited in Fig. 7(a), there are a few widely separated bright spots at 5 mN m−1. The restructuring of the monolayer is attributed to the initial spontaneous aggregation and conformation of the PEG chains due to their submergence in the water subphase during compression.1 The aggregations of dark regions among the hydrophobic chains are supposed to be PEG chains. As the surface pressure increases to 30 mN m−1, a reticular structure is observed in Fig. 7(b). The film is compact, and more bright regions appear with the compression. The block chains are rearranged at the interface, and the motion of the copolymer aggregates inside the film may result in a conformation change. When the surface pressure rises up to 62 mN m−1, the formation of densely packed structures is caused by the lateral compression of the relatively incompressible hydrophobic chains.
The roughness values of the three LB films of copolymer-2 increase from 299.2, 419.6 to 974.1 pm. From the 3D images and the roughness data, it is found that the roughness of the aggregation is increased by enhancing the surface pressure. This is interpreted as either the molecule being forced to alter its conformation due to the vicinity of its nearest neighbors with the increasing compression, or a densification of the packing of the copolymer molecules at a given surface pressure derived from the LB depositions. The aggregates’ transformation change from relatively dispersive structures to continuous structures upon compression is due to the rebuilding of the hydrophobic chains by the lateral compression.
From the results above, the changes in the morphologies obtained from the different copolymers at the same surface pressure and different transferred regions of identical copolymers are apparent. The block ratio and chain length of the copolymers and the surface pressure play an important role in the morphologies of the LB films, and this is similar to the result in previous research by Deschênes et al.4
3.4. Proposed packing model for the aggregation formation
From the analyses above, the packing model for the pentablock copolymer aggregate at the air–water interface is proposed in Fig. 8. | ||
| Fig. 8 Proposed packing model for the structure evolution for the pentablock copolymer based on the isotherms and AFM images. | ||
At Π ≈ 0 mN m−1, the copolymers are spread completely with disordered dispersion and occupy a large surface area as depicted in Fig. 8(a). Lateral compression causes an increase in the polymer density, and the orientation of the molecules may occur as shown in Fig. 8(b). In this case, the copolymer chains float on the water surface and adopt a flattened conformation on the water surface with maximum contact with the water surface (pancake conformation). Upon further compression, the copolymer molecules start to contact each other (Fig. 8(c)), and the PEG chains are progressively dissolved in the water subphase; in this circumstance, the underneath hydrophobic groups are contacted, making the surface pressure and compression modulus increase. As compression proceeds, compared to the rigid PMMA and PTFEMA chains, the smooth PEG chains begin to stretch and mostly loop into the water as shown in Fig. 8(d). Further compression causes the extrusion of the PMMA chains as shown in Fig. 8(e). Parts of the PMMA chains detach on the water surface and aggregate into thicker domains, which represents a transition from the pancake to the brush conformation of the monolayer. The chains strongly interact so the surface pressure rapidly increases. As shown in Fig. 8(f) the hydrophobic groups align vertically with further compression, the hydrophobic chains are densely packed and kept in touch with each other. At this point, the monolayer completely covers the surface in a uniform phase and the copolymer molecules reorganize into a brush conformation. The last compression leads to the film collapse which is attributed to the over-compression of the relatively incompressible hydrophobic chains (Fig. 8(g)),7 and the compression modulus starts to decrease.
4. Conclusions
In this paper, the interfacial rheology and aggregation behaviour of the amphiphilic CBABC-type pentablock copolymers PTFEMA-b-PMMA-b-PEG-b-PMMA-b-PTFEMA with different block ratios and chain lengths are investigated at the air–water interface.The influence of the block ratio and chain length on the interfacial rheology of the Langmuir films is studied via continuous compression, successive addition and step compression methods. It is found that copolymer-1 and copolymer-2 show four phase transition regions in the Π–MMA isotherms, while copolymer-3 lacks the collapse region. The higher the hydrophobic ratio and hydrophobic chain length are, the larger the surface pressure at the same mean molecular area is, as well as the limiting mean molecular area. Compared to successive addition, higher values of the surface pressure and modulus are observed in continuous compression due to the strongly interacting chains.
In addition, the relaxation of the monolayer is investigated through step compression. It is found that there are two relaxation processes (fast and slow relaxation processes) in the second and third relaxation curves, while only one relaxation process in the first curve. The fast relaxation process is attributed to the adsorption–desorption exchange of molecules and polymer segments on the surface. Meanwhile, the slow relaxation process is dominated by slower reconformations of the adsorbed macromolecules inside the adsorption layer. Furthermore, the LB films prepared from the three copolymers at various surface pressures have a variety of morphologies such as macroporous, rugged, reticular and discontinuous continent structures resulting from the block ratio, chain length and surface pressure. Finally, the packing model for the pentablock copolymer aggregates at the air–water interface is proposed.
Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant no. 51372206, 51301139), Natural Science Foundation of Shaanxi Province (Grant no. 2013JM2012), Innovation Project of Science and Technology of Shaanxi Province (Grant no. 2013KTCG01-14) and NPU Foundation for Fundamental Research (Grant no. 3102014JCQ01089).Notes and references
- M. J. Felipe, N. Estillore, R. B. Pernites, T. Nguyen, R. Ponnapati and R. C. Advincula, Langmuir, 2011, 27, 9327–9336 CrossRef CAS PubMed.
- A. Maestro, F. Ortega, F. Monroy, J. Krägel and R. Miller, Langmuir, 2009, 25, 7393–7400 CrossRef CAS PubMed.
- T. J. Joncheray, K. M. Denoncourt, M. A. R. Meier, U. S. Schubert and R. S. Duran, Langmuir, 2007, 23, 2423–2429 CrossRef CAS PubMed.
- L. Deschênes, M. Bousmina and A. M. Ritcey, Langmuir, 2008, 24, 3699–3708 CrossRef PubMed.
- C. P. Glagola, L. M. Miceli, M. A. Milchak, E. H. Halle and J. L. Logan, Langmuir, 2012, 28, 5048–5058 CrossRef CAS PubMed.
- X. Wang, X. Ma and D. Zang, Soft Matter, 2013, 9, 443–453 RSC.
- W. Lee, S. Ni, J. Deng, B.-S. Kim, S. K. Satija, P. T. Mather and A. R. Esker, Macromolecules, 2007, 40, 682–688 CrossRef CAS.
- J. Y. Park and R. C. Advincula, Soft Matter, 2011, 7, 9829–9843 RSC.
- I. I. Perepichka, A. Badia and C. G. Bazuin, ACS Nano, 2010, 4, 6825–6835 CrossRef CAS PubMed.
- E. W. Price, S. Harirchian-Saei and M. G. Moffitt, Langmuir, 2010, 27, 1364–1372 CrossRef PubMed.
- S. Harirchian-Saei, M. C. P. Wang, B. D. Gates and M. G. Moffitt, Langmuir, 2010, 26, 5998–6008 CrossRef CAS PubMed.
- I. I. Perepichka, K. Borozenko, A. Badia and C. G. Bazuin, J. Am. Chem. Soc., 2011, 133, 19702–19705 CrossRef CAS PubMed.
- L. Zhao, C. Feng, X. Pang, J. Jung, M. C. Stefan, P. Sista, R. Han, N. Fang and Z. Lin, Soft Matter, 2013, 9, 8050–8056 RSC.
- J. L. Logan, P. Masse, B. Dorvel, A. M. Skolnik, S. S. Sheiko, R. Francis, D. Taton, Y. Gnanou and R. S. Duran, Langmuir, 2005, 21, 3424–3431 CrossRef CAS PubMed.
- J. L. Logan, P. Masse, Y. Gnanou, D. Taton and R. S. Duran, Langmuir, 2005, 21, 7380–7389 CrossRef CAS PubMed.
- R. B. Cheyne and M. G. Moffitt, Langmuir, 2005, 21, 5453–5460 CrossRef CAS PubMed.
- R. B. Cheyne and M. G. Moffitt, Langmuir, 2006, 22, 8387–8396 CrossRef CAS PubMed.
- L. Zhao and Z. Lin, Soft Matter, 2011, 7, 10520–10535 RSC.
- H. Hilles, A. Maestro, F. Monroy, F. Ortega, R. G. Rubio and M. G. Velarde, J. Chem. Phys., 2007, 126, 124904 CrossRef PubMed.
- A. Maestro, L. J. Bonales, H. Ritacco, T. M. Fischer, R. G. Rubio and F. Ortega, Soft Matter, 2011, 7, 7761–7771 RSC.
- D. Zang, A. Stocco, D. Langevin, B. Wei and B. P. Binks, Phys. Chem. Chem. Phys., 2009, 11, 9522–9529 RSC.
- A. Maestro, E. Guzmán, E. Santini, F. Ravera, L. Liggieri, F. Ortega and R. G. Rubio, Soft Matter, 2012, 8, 837–843 RSC.
- C. Stefaniu, G. Brezesinski and H. Möhwald, Adv. Colloid Interface Sci., 2014, 208, 197–213 CrossRef CAS PubMed.
- J. Maldonado-Valderrama, A. Martín-Rodriguez, M. J. Gálvez-Ruiz, R. Miller, D. Langevin and M. A. Cabrerizo-Vílchez, Colloids Surf., A, 2008, 323, 116–122 CrossRef CAS PubMed.
- B. A. Noskov, G. Loglio and R. Miller, Adv. Colloid Interface Sci., 2011, 168, 179–197 CrossRef CAS PubMed.
- B. A. Noskov, Curr. Opin. Colloid Interface Sci., 2010, 15, 229–236 CrossRef CAS PubMed.
- C. Kotsmar, V. Pradines, V. S. Alahverdjieva, E. V. Aksenenko, V. B. Fainerman, V. I. Kovalchuk, J. Krägel, M. E. Leser, B. A. Noskov and R. Miller, Adv. Colloid Interface Sci., 2009, 150, 41–54 CrossRef CAS PubMed.
- J. Miñones, M. M. Conde, E. Yebra-Pimentel and J. M. Trillo, J. Phys. Chem. C, 2009, 113, 17455–17463 Search PubMed.
- T. Morioka, O. Shibata and M. Kawaguchi, Langmuir, 2010, 26, 18189–18193 CrossRef CAS PubMed.
- T. Morioka, O. Shibata and M. Kawaguchi, Langmuir, 2010, 26, 14058–14063 CrossRef CAS PubMed.
- A. Maestro, H. M. Hilles, F. Ortega, R. G. Rubio, D. Langevin and F. Monroy, Soft Matter, 2010, 6, 4407–4412 RSC.
- K. N. Witte, S. Kewalramani, I. Kuzmenko, W. Sun, M. Fukuto and Y. Y. Won, Macromolecules, 2010, 43, 2990–3003 CrossRef CAS.
- E. Spigone, G.-Y. Cho, G. G. Fuller and P. Cicuta, Langmuir, 2009, 25, 7457–7464 CrossRef CAS PubMed.
- R. Miller, J. Ferri, A. Javadi, J. Krägel, N. Mucic and R. Wüstneck, Colloid Polym. Sci., 2010, 288, 937–950 CAS.
- T. Naolou, K. Busse, B.-D. Lechner and J. Kressler, Colloid Polym. Sci., 2014, 292, 1199–1208 CAS.
- L. R. Arriaga, F. Monroy and D. Langevin, Soft Matter, 2011, 7, 7754–7760 RSC.
- Y. Guo, T. Chen, N. Zhao, Y. Shang and H. Liu, Colloid Polym. Sci., 2013, 291, 845–854 CAS.
- J. Juárez, S. Goy-López, A. Cambón, M. A. Valdez, P. Taboada and V. C. Mosquera, J. Phys. Chem. C, 2010, 114, 15703–15712 Search PubMed.
- W. M. de Vos, A. de Keizer, J. M. Kleijn and M. A. Cohen Stuart, Langmuir, 2009, 25, 4490–4497 CrossRef CAS PubMed.
- S. Vanslambrouck, B. Clement, R. Riva, L. H. Koole, D. G. M. Molin, G. Broze, P. Lecomte and C. Jerome, RSC Adv., 2015, 5, 27330–27337 RSC.
- X. Wang, G. Wen, C. Huang, Z. Wang and Y. Shi, RSC Adv., 2014, 4, 49219–49227 RSC.
- Y. Seo, C. Y. Cho, M. Hwangbo, H. J. Choi and S. M. Hong, Langmuir, 2008, 24, 2381–2386 CrossRef CAS PubMed.
- B. Chung, H. Choi, H. W. Park, M. Ree, J. C. Jung, W. C. Zin and T. Chang, Macromolecules, 2008, 41, 1760–1765 CrossRef CAS.
- Y. Sasaki, N. Aiba, H. Hashimoto and J. Kumaki, Macromolecules, 2010, 43, 9077–9086 CrossRef CAS.
- N. Mitsui, T. Morioka and M. Kawaguchi, Colloids Surf., A, 2012, 395, 248–254 CrossRef CAS PubMed.
- A. Maestro, F. Ortega, R. G. Rubio, M. A. Rubio, J. Krägel and R. Miller, J. Chem. Phys., 2011, 134, 104704 CrossRef CAS PubMed.
- Z. Wang, G. Wen, F. Zhao, C. Huang, X. Wang, T. Shi and H. Li, RSC Adv., 2014, 4, 29595–29603 RSC.
- G. Li Destri, F. Miano and G. Marletta, Langmuir, 2014, 30, 3345–3353 CrossRef CAS PubMed.
- K. Busse, C. Peetla and J. Kressler, Langmuir, 2007, 23, 6975–6982 CrossRef CAS PubMed.
- Z. Li, X. Ma, D. Zang, B. Shang, X. Qiang, Q. Hong and X. Guan, RSC Adv., 2014, 4, 49655–49662 RSC.
- A. Stocco, E. Rio, B. P. Binks and D. Langevin, Soft Matter, 2011, 7, 1260–1267 RSC.
- D. Zang, E. Rio, D. Langevin, B. Wei and B. Binks, Eur. Phys. J. E: Soft Matter Biol. Phys., 2010, 31, 125–134 CrossRef CAS PubMed.
- H. M. Hilles, M. Sferrazza, F. Monroy, F. Ortega and R. G. Rubio, J. Chem. Phys., 2006, 125, 074706 CrossRef PubMed.
- D. Langevin and F. Monroy, Curr. Opin. Colloid Interface Sci., 2010, 15, 283–293 CrossRef CAS PubMed.
- K. Kita-Tokarczyk, M. Junginger, S. Belegrinou and A. Taubert, in Self Organized Nanostructures of Amphiphilic Block Copolymers II, ed. A. H. E. Müller and O. Borisov, Springer Berlin, Heidelberg, 2011, vol. 242, pp. 151–201 Search PubMed.
- B. Gzyl-Malcher, M. Filek and G. Brezesinski, Langmuir, 2011, 27, 10886–10893 CrossRef CAS PubMed.
- F. Monroy, F. Ortega, R. G. Rubio and M. G. Velarde, Adv. Colloid Interface Sci., 2007, 134–135, 175–189 CrossRef CAS PubMed.
- G. L. Gaines, Insoluble monolayers at liquid-gas interfaces, Interscience Publishers, New York, 1966 Search PubMed.
- N. Chaudhary and R. Nagaraj, J. Colloid Interface Sci., 2011, 360, 139–147 CrossRef CAS PubMed.
- F. Monroy, F. Ortega, R. G. Rubio, H. Ritacco and D. Langevin, Phys. Rev. Lett., 2005, 95, 056103 CrossRef.
- H. M. Hilles, F. Ortega, R. G. Rubio and F. Monroy, Phys. Rev. Lett., 2004, 92, 255503 CrossRef.
- B. Martín-García, M. M. Velázquez, J. A. Pérez-Hernández and J. Hernández-Toro, Langmuir, 2010, 26, 14556–14562 CrossRef PubMed.
- Y. J. Chen, T. Liu, G. Y. Xu, J. Zhang, X. R. Zhai, J. Yuan and Y. B. Tan, Colloid Polym. Sci., 2015, 293, 97–107 CAS.
- H. Zhu, J. Matsui, S. Yamamoto, T. Miyashita and M. Mitsuishi, Soft Matter, 2015, 11, 1962–1972 RSC.
- F. Monroy, H. M. Hilles, F. Ortega and R. G. Rubio, Phys. Rev. Lett., 2003, 91, 268302 CrossRef.
- G. A. Georgiev, N. Yokoi, S. Ivanova, V. Tonchev, Y. Nencheva and R. Krastev, Soft Matter, 2014, 10, 5579–5588 RSC.
- N. Tschoegl, The phenomenological theory of linear viscoelastic behavior: an introduction, Springer Verlag, Berlin, 1989, pp. 445–457 Search PubMed.
- D. Zang and Y. Zhang, Sci. China: Phys., Mech. Astron., 2011, 54, 1587–1592 CrossRef CAS.
- Y. Y. Wang, Y. H. Dai, L. Zhang, L. Luo, Y. P. Chu, S. Zhao, M. Z. Li, E. J. Wang and J. Y. Yu, Macromolecules, 2004, 37, 2930–2937 CrossRef CAS.
- S. I. Lopes, A. M. Gonçalves da Silva, P. Brogueira, S. Piçarra and J. Martinho, Langmuir, 2007, 23, 9310–9319 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Π–MMA isotherm of copolymer-3 with a spreading amount of 0.025 mg and BAM image of a monolayer of copolymer-1 at the collapse region (MMA = 33.0 nm2). See DOI: 10.1039/c5ra08109b |
| This journal is © The Royal Society of Chemistry 2015 |



