The molecular mechanism of conformational changes of the triplet prion fibrils for pH

Abstract

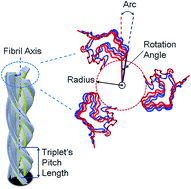
The HET-s prion fibril, which is found in the filamentous fungus Podospora anserina, exhibits conformational changes due to variations in pH. Here, we explain the effects of changing pH on the conformational changes of fibrils through the fundamental eigenmodes of the fibrils, in particular the torsional and bending modes, using a parameter free elastic network model. In particular, the motion resulting from these fundamental eigenmodes is found to be very similar to the conformational changes stimulated by pH variations as shown in previous experimental results. Finally, we calculated the mechanical properties of the triplet prion fibrils to elucidate its variations in the infectious state.

---

Introduction

Amyloid fibrils are misfolded proteins which cause various neurodegenerative diseases. Prion is a well-known amyloid which causes bovine spongiform encephalopathy (mad cow disease), Creutzfeldt–Jakob disease, Kuru disease, etc. A prion form of heterokaryon incompatibility protein-s (HET-s) aggregates and forms fibril shaped structures such as other amyloid proteins.¹ Recently, it is reported that HET-s prion has 2-D ordered structures and 1-D fibrils in different pH conditions.²

Daggett et al.³ observed Aβ-sheet forming during 10 ns equilibration in a low pH condition with molecular dynamics (MD) simulation. Understanding of the β-sheet forming may give insights into the mechanisms governing inhibition prion propagation. In that research, pH-induced conformational changes for prion protein revealed the mechanism of conversion from PrP^C to PrP^Sc which is the origin of the fatal infectiousness of prion protein.⁴ The MD shows the protofibril formation mechanism of the PrP^Sc whose building block was a PrP^Sc trimer that is composed of β-sheet, α-helix and tails on its inner and outer surfaces.³ The trimer structure had characteristics of prion fibrils that is shown in the HET-s prion fibrils whose cross-sectional shape is triangular.¹ Because of the triangular shape of HET-s, it can have three fundamental bending modes.⁵ In addition, the direction of conversion from PrP^C to PrP^Sc follows the eigenmodes of PrP^C which are analyzed by normal mode analysis.⁶ This result is interesting because normal mode analysis cannot account for chemical effects such as pH; however conversion from PrP^C to PrP^Sc was depicted by eigenmodes. This implies conversion to PrP^Sc is assisted by environmental condition such as pH, though the ability to change to the scrapie form is intrinsic to the prion structure.⁷

The HET-s prion fibrils in the filamentous fungus Podospora anserina exhibit hierarchical structures from 1-D to the 2-D ordered structure and those hierarchy structures are related to the infectivity of the prion.^1,8 When HET-s(218–289) dimers form a left-handed singlet fibril, the fibril has infectivity which is reflected by the high mechanical properties⁵ and the exposed lateral surface of the fibril.² The enhanced mechanical properties arise because the left-handed twisting pattern of the HET-s prion fibrils have higher hydrogen bond density rather than right-handed normal fibrils.⁵ Moreover, singlet HET-s fibrils gather to form higher hierarchical structure as triplet fibrils or 2-D angled-layer structures according to the environmental pH conditions.² The triplet fibrils exhibit conformational changes for different pH conditions, which are similar to the well-known breathing mode of tubular structures. Breathing mode is a radial motion that changes the radius of the structure, and has been observed in allosteric transitions of chaperonin GroEL, and hollow nanostructures such as carbon nano tube (CNT). It is obvious that there is a large difference in the source of breathing mode of these structures, because the breathing mode of GroEL is due to allosteric conformational change of each subdomains. However the common point is that these structures are a hollow shaped, and have breathing mode.

The low-frequency normal modes from normal mode analysis (NMA) of elastic network model (ENM) is effectively applied to various protein researches such as conformational dynamics of proteins, and mechanical property measurements.^9,10 The ENM is a C_α based coarse-grained model whose potential is harmonic between each C_α atom within the cut-off distance. Although the ENM model is simplistic, it has been applied to study the structure–function relationship of large proteins to understand the transition between open and closed form for induced fit model observed upon ligand binding.¹¹ Moreover, the ENM is valuable to show the global dynamics of protein and its mechanical properties in conjunction with continuum mechanics theories, shedding light on the structure–property relationship of protein. The fundamental mode shapes such as bending, torsional mode and its mechanical properties of amyloid fibrils, prion fibrils and microtubules are studied using ENM with Euler–Bernoulli beam theory which are comparable to the experiments.^12–14 Especially, the mechanical properties difference due to the polymorphism of amyloid, which is the possibility of chemical bond configuration in the steric zipper can be observed by the ENM.¹⁴ Also, ENM can show that the HET-s singlet prion fibrils exhibit superior mechanical properties than normal protein fibrils originated by the distinct helical shapes of the fibrils whether left-handed or right-handed.⁵ One research of Mizuno group's gave a topology information about the HET-s singlet prion fibrils being able to conform diverse formations for pH conditions.² The HET-s single fibrils formed triplet fibrils which look like a yarn at low pH condition, and angled-layered structure was formed at neutral pH condition.² In addition, the HET-s triplet fibrils have an ability of infection at pH 3. However, the HET-s triplet fibrils in pH 2, which also looks similar with those in pH 3, do not show any infectious feature. An explanation for that interesting feature has not been revealed, which is one of the objectives of the present research.

Here, we employed the parameter free ENM (pfENM)¹⁵ to describe the conformational changes of triplet HET-s prion fibrils and obtain its mechanical properties. The pfENM is a specific branch of ENM which does not consider the cut-off distance. It is due to the special structural form of HET-s triplet, with large spaces between single fibril which is not described well by the properly used cut-off distance of ENM. So it was more efficient than normal ENM, to show the mechanochemical characteristics depending on the structures impacted by pH conditions. We used 2KJ3,¹⁶ which is a high-resolution structure of the HET-s(218–289) prion in its amyloid form obtained by solid-state NMR, to rebuild a computational model of the HET-s triplet fibrils. The pH 2 triplet is reconstructed by referring to the experimental data,² using only C_α atoms of 2KJ3.

Model

To prepare the model of HET-s triplet fibril for our simulation, we used PDB code 2KJ3,¹⁶ which is a high-resolution structure of the HET-s(218–289) prion in its amyloid form obtained by solid-state NMR. The pH 2 triplet is reconstructed by referring to the experimental data,² using only C_α atoms of 2KJ3.¹⁶ In the Fig. 1, the schematic of triplet fibril is shown where the radius refers to the shortest distance from the fibril axis, the rotation angle is the twisted angle between two adjacent subunits, arc is calculated with rotation angle and radius, and refers to the twisted distance between two adjacent subunits in singlet. The pitch length of the triplet fibril is the one-third pitch length of the singlet fibril. Each of the singlet fibrils are rotated 120 degrees based on the fibril axis. Top view is part of the reconstructed structure using the C_α atoms of 2KJ3.¹⁶ It shows the two intact subunits of the three singlet fibrils. The triplet fibril was recomposed by using only C_α atoms from the monomer of 2KJ3, and used 8640 C_α atoms in total (a single monomer uses 72 C_α atoms, and there were 40 stacks in total). We built four models in different length to find the length effect to the triplet fibril. Model 1 has 40 stacks which is 112 nm in length, model 2 and model 3 have 60 and 92 stacks respectively. Finally, the longest model 4 has 117 stacks, which is 329.47 nm.

Fig. 1 The schematic diagram of the HET-s triplet fibril. We construct the HET-s triplet fibril according to the experimental parameters² such as fibril axis, radius, rotation angle per subunit, arc per subunit and triplet's pitch length. One subunit of triplet fibril is colored red. A triplet fibril consist of three singlet fibrils which are reconstructed by using C_α atoms of 2KJ3.¹⁶ Radius is the length between the fibril axis and the closest residue of triplet fibril. Rotation angle/subunit means the twisted angle between first (red) and second (blue) subunit of triplet fibril. Arc per subunit represents the calculated length of arc by using rotation angle per subunit.

Methods

Parameter free elastic network model (pfENM)

The elastic network model (ENM) is a simple coarse-grained model which describes the protein structure with C_α atoms only, and interaction of atoms within the cut-off distance is described with harmonic potential.^9,17,18 Despite its simplicity, ENM describes protein motion with low-frequency normal modes well. However, the range of cut-off distance is important with analysis using ENM, and usually 7–15 Å is applied for various ENM analyses. However, when a short cut-off distance is used, the atomic interactions are not sufficiently strong to induce. In contrast, large cut-off distance makes the structure stiff which leads to an increase of the frequencies for each mode. For the both cases, small or large cut-off distance, are not suitable for ENM. However, HET-s triplet in this research has a large distance of ∼22 Å between singlet fibrils. Applying ENM to HET-s triplet required cut-off distance larger than 22 Å, which is known to be not suitable. Indeed, we tried to apply this cut-off distance but it did not describe the normal mode well. So we applied pfENM to obtain the fundamental low-frequency normal mode of HET-s triplet. The difference of ENM and pfENM is application of cut-off distance. For ENM, atom interaction strength inside cut-off distance is the same, while the interaction strength of pfENM depends on the distance. In the ENM, the Hessian matrix (H) which contains the second derivative of harmonic potentials is used to represent the anisotropic fluctuations of proteins. The harmonic potential of ENM can be described as following.here, γ is the force constant between i-th residue and j-th residue, s_ij is the distance between i-th residue and j-th residue, and 0 indicates the equilibrium state.

The Hessian matrix consists of n by n components each of size 3 by 3, which leads the total size is 3N × 3N. The i and j components of H is given as,

where, x_i, y_i, and z_i are the Cartesian components of i-th residue and V represents the harmonic potential energy of the network which is made of alpha carbons described in eqn (1). As shown in eqn (2), Hessian matrix is a second-derivative of potential energy acting as a stiffness matrix.

Until this step, the basic equations are common for ENM and pfENM. In this stage we apply the concept of pfENM, all pairs of interactions between C_α are considered and there is no cut-off distance, so that its computational burden is higher than the original ENM. Despite this disadvantage, pfENM provides reliable stiffness of structure with large gap such as HET-s triplet fibril. Previous study from Yang et al.¹⁹ shows how well the modes of pfENM are related to conformational changes observed by experimental methods. In the pfENM, each elements of the Hessian matrix (H^pf_ij) is given as,

H^pf_ij = H_ijr_ij⁻ⁿ, (n = 1, 2, 3, …), (3)

where the best power (n) dependence of the pfENM for the large conformational transitions are in the range of r_ij⁻⁶ to r_ij⁻⁸. We modified pfENM to predict the conformational change of pH 2 triplet fibrils and to get accurate mechanical properties. To obtain proper eigenvalues we used a modified matrix, which was described in our previous work as,^5,14

H^pf*_ij = c*·H_ijr_ij⁻⁶, (4)

where c* is a constant which is approximated by calculating the mechanical properties of HET-s singlet from our previous study. Using the Hessian matrix from eqn (4), we solved eigenvalue problem to obtain the normal mode of HET-s triplet fibril.

Results

Torsional mode of HET-s triplet fibril

In Fig. 2, the conformational change of the triplet fibril from pH 2 to pH 3 based on the low-frequency normal mode is shown. As the pH increased from 2 to 3, the radius of the triplet fibril increased, and the triplet-forming singlet also had increased rotation angle/subunit value. The conformational change of HET-s triplet fibril from pH 2 to pH 3 seems to be in torsional mode. Also using the calculated torsional mode showed similar conformational change of the pH 2 model into the pH 3 model. The torsion mode (7 or 9th mode depending on the length), was found to have the dominant effect while it was slightly coupled by a bending mode. Due to the coupled bending mode, the breathing mode for the triplet fibril can be observed as pH increases from 2 to 3. Such conformational change along the radial direction can be called the “breathing mode”.

Fig. 2 The conformational change of HET-s triplet fibril pH 2 to pH 3 which is induced by torsional mode shape. It is comparable to the experimental study² that shows the conformational change of HET-s triplet fibrils according to the changes of pH condition. Top and lateral views at pH 2 are shown on the left side and pH 3 is on the right side. The torsional mode has the largest effect on conformational change. Radial breathing mode can be observed by the coupled mode.

In the Table S1,† the structural parameter for HET-s triplet fibrils are shown for pH 2 and 3. Here, “experiment” represents the data from the experimental studies on the triplet fibrils² and the “model” refers to the data set of reconstruction for triplet fibrils for computational model.

We calculated fundamental normal modes for HET-s triplet fibrils to understand the motions. In Fig. 3 we plotted eigenvalues of torsional modes obtained from HET-s triplet fibrils in different lengths. For the structures in longitudinal shapes usually have bending motion for the lowest frequency normal modes (7th mode). It is interesting that model 1 depicts torsional modes in the 7th mode, which usually describes bending modes in common. Model 2, 3, and 4 depicted 9th mode as torsional mode. From this result, we can conclude that model 1 is too short to observe fully beam-like behavior. But for the models longer than model 1, they have bending modes at 7th mode, and the torsional mode is shifted to 9th mode. It means HET-s triplet behaves as hollow beam structure when it is at least ∼168 nm long. It is obvious that as the structure becomes longer, the eigenvalue of the torsional mode converges. Convergence of the eigenvalue also implies convergence of its related mechanical properties.

Fig. 3 Eigenvalue of torsional modes calculated from HET-s triplet fibril in four different length models. The length of fibril is increased as the model index is increased. Torsional mode is appeared in 7th mode of model 1, but mode index is increased to 9th mode from model 2 to model 4. As the fibril length is increased, the eigenvalue of torsional mode is stabilized.

Describing conformational change with torsional mode

For validation of the role of the torsional mode to the conformational change of HET-s triplet fibril, we calculated the overlap (O_i)²⁰ that represents the similarity between the direction of global conformational displacement in experiment and the direction obtained with normal mode analysis, using the equation below.where v_i is the ith eigenvector and Δx is the displacement vector between the experimental reference structure of pH 2 and pH 3 triplets. In the low-frequency region, except for the first six rigid body modes, the overlap value of the torsion mode exhibited the highest value shown in the Fig. 4. As we expected, conformational change of HET-s triplet fibril from pH 2 to pH 3 is related to torsional mode. Also it is interesting that torsional mode of relatively short fibrils (model 1 and model 2) had overlap of ∼0.5, while it of longer fibrils (model 3 and model 4) exhibited overlap of ∼0.8. For model 1 and model 2, 18th and 23rd modes were also confirmed as higher order torsional modes. It seems that first torsional mode is effective when the triplet fibril becomes longer which is shown by higher overlap value. Bending and torsion modes are fundamental modes for fibril structures, and they are usually known to have an important role in structural behavior of amyloid fibrils such as Amyloid beta (Aβ), human Islet Amyloid Poly Peptide (hIAPP) fibrils, and microtubules.^{5,13,19,21,22} In our overlap calculation it is found that bending mode is not related to the conformational change due to pH change. Usually the lowest frequency mode (7th mode) display bending mode, 7th mode of model 1 was close to torsional mode. Moreover, bending mode of other models (model 2, 3, and 4) displayed no relationship with the conformational change of HET-s triplet fibril. Therefore, the pH induced conformational change of HET-s triplet fibril can be explained by the torsional mode which is related to breathing motion. There were researches about chemical oscillators being able to exert influence on conformational change of proteins and their motion.^7,23,24 In our research, we measured formational similarity with fundamental modes of the biological structures at several tens of GHz based on our calculation. Natural frequencies which depend on structure's geometries^5,13,14 can be affected by chemical oscillators. In the range of fundamental natural frequencies of the HET-s fibril, HET-s fibrils have a possibility of behaving breathing motion, and it would be interesting to determine if a breathing motion of HET-s triplet could be observed with a chemical oscillator.

Fig. 4 (a) Cumulative overlap between normal modes calculated from pH 2 model and direction vector between pH 2 to pH 3 model. All of the torsional modes from models behave as the major conformational change mode. For all 4 models, torsional mode (7th mode for model 1, and 9th mode for the others) has overlap over 0.5 showing the largest portion of total amount. (b) Conformational changes from pH 2 to pH 3 induced by each modes for model 1. Arrows and circles are drawn to show the differences changed.

Measuring mechanical properties of HET-s triplet fibril

Here, we measured mechanical properties of HET-s triplet fibril to compare the effect of conformation change due to the pH difference. For obtaining the mechanical properties for fundamental mode shapes, the Euler–Bernoulli beam theory is used to estimate the bending rigidities and torsional modulus for HET-s triplet fibrils. Here, pH 2 and pH 3 triplets are considered as a hollow cylinder like microtubules.¹² Normally, following equations are used to obtain the bending rigidity and the torsional modulus for the triplet. The natural frequencies corresponding to bending, torsion modes can be obtained from equations given as,^25–27here, f^B and f^T are the bending and torsional natural frequencies calculated by NMA, L is the length of the triplet, ρ is mass density, A is cross-sectional area for fibrils. And α is a boundary condition depends on mode numbers. E_B, I, and G_T are indicating that the bending elastic modulus, cross-sectional moment of inertia and torsional shear modulus, respectively. By assuming as a hollow cylinder and applying the Euler–Bernoulli beam theory, the bending rigidity and the torsional modulus were obtained. The bending rigidity of the triplet fibrils is higher than that of the singlet fibrils which are in the previous study,⁵ due to a higher thickness of triplet fibrils. Also, the torsional modulus of triplet fibrils is comparable to the microtubules.¹⁹

In Fig. 5, pH 2 triplet fibrils have higher mechanical properties than that of the pH 3 triplet fibrils. The torsional modulus for torsion mode, which exhibits more dominant effect in the conformational change of the triplet fibrils, has a higher value in pH 2 structure. It indicates that pH 2 fibril is more stable than the pH 3 structure is. A fact that pH 3 triplet fibrils have a higher tendency to be disentangled than that of pH 2 triplet fibrils have is confirmed from the previous studies,² and such phenomenon can be explained with the result of weak interaction between the singlet fibrils which are composing the triplet fibrils. When triplet fibrils are affected by the change of pH surroundings, pH 3 triplet fibrils which have lower bending rigidity can be easily bent, and more easily separated. That structural change can cause the lower interaction between singlet fibrils. The motion of winding-unwinding of the triplet is dominantly affected by the torsional mode, and the fact that the direction of the conformational change which is induced by the real chemical reaction is highly comparable to the direction of torsional mode shapes which was estimated with the pfENM in this research. In addition, a tendency of pH 3 triplet fibrils being easily disentangled can be explained with lower torsional modulus. As a result, a reduction in the bending rigidity and torsional modulus of pH 3 triplet fibrils, as compared with pH 2 triplet fibril, are connected to the infectious mechanism of pH 3 triplet fibrils.

Fig. 5 Mechanical properties of pH 2 and pH 3 HET-s triplet fibrils. Bending rigidity (blue) and torsional elastic modulus (red) are shown. The pH 2 fibril has higher mechanical properties than pH 3.

Moreover, we calculated the mechanical properties of the triplet fibrils in pH 2 condition in different lengths (model 1 to model 4). Compared to the singlet fibril, the triplet fibril structure has larger pitch length which makes the structure longer. We calculated bending rigidity (Fig. 6(a)) and torsional modulus (Fig. 6(b)) for four different length models using the following equation based on Timoshenko beam theory:

here E_B is effective bending elastic modulus dependent to length, E⁰_B is the length-independent bending elastic modulus, G_s is the intrinsic shear modulus, I, A, and L represent the cross-sectional moment of inertia, the cross-sectional area, and the length, respectively, a and b are the boundary condition dependent constants, and c is a shear coefficient that depends on the cross-sectional shape. Bending rigidity of 4 models were perfectly fitted with the Timoshenko's beam theory. Torsional modulus is also calculated for 4 models. Torsional modulus is decreased as the triplet fibril becomes longer. Weakening of torsional modulus in longer triplet fibril may cause conformational change due to pH change easily.

Fig. 6 Mechanical properties of HET-s triplet fibril in pH 2 condition. (a) Bending rigidity for different length models fitted to Timoshenko's beam theory and (b) torsional modulus for different length models.

In our previous study, we determined that the singlet of the HET-s prion nano fibril has several fundamental mode shapes and estimated some mechanical properties.⁵ In particular we found that the direction of the bending mode for the singlet has three unique configurations because of its triangular cross-sectional shape and estimated several mechanical properties on the fibril length. A feature of the singlet fibrils, which is changed its conformation due to the pH condition, is revealed in the experimental study.² Especially those singlet fibrils compose the triplet fibrils in the condition of pH 2 and pH 3. The pH 3 triplet has more un-winded form than the pH 2 triplet fibril and it is easy for the pH 3 triplet fibril to be changed into singlet fibril, which has previously been related to the infectious feature. HET-s triplet fibril changes its conformation in the low pH domain. We also showed that the pH 3 triplet is more unwound than the pH 2 triplet.

Conclusion

In this research, we quantified the bending rigidity and torsional modulus for HET-s prion triplet fibrils at different pH 2 and 3 using pfENM in conjunction with continuum beam theory. We found that the conformational changes in going from pH 2 fibrils to pH 3 fibrils is due to the fundamental eigenmodes, and specifically the torsional modes. From this result, the directions of conformational changes of the fibrils driven by pH changes could be described by the low-frequency normal modes of the triplet fibrils, and a direct connection as to how the mechanical property differences due to the pH changes affect the infectious characteristics of prion was established. The HET-s triplet fibril changed its conformation during pH change, while our pfENM calculated similar motion of conformational change without chemical effect of pH change. We may conclude that pH plays a key role in initiating the conformational change of HET-s triplet fibril, while the basic structural motion is highly affected by fundamental modes of motion. The possibility for the HET-s triplet fibril to be utilized in applications could be discussed, in that its breathing motion, which is due to the pH variation, can cause the change of its mechanical properties and the fact that the diameter of that nano-scaled tube can be controlled. We close by noting the importance of temperature on the conformation changes of proteins, a factor that was not considered in the present work. Interestingly, the torsional modes of metallic nanowires with geometries similar to the HET-s triplet were strongly impacted by temperature changes.²⁸ This motivates future studies involving temperature effect on the vibrational modes of HET-s triplets, studies which are currently underway.

Acknowledgements

S. N. gratefully acknowledges the financial support from NRF under Grant nos 2007-0056094, 2014R1A2A1A11052389. G. Y. is grateful to the financial support from NRF under Grant no. 2012R1A1A2038373 and Korea University Grant.

References

1. C. Wasmer, A. Lange, H. Van Melckebeke, A. B. Siemer, R. Riek and B. H. Meier, Science, 2008, 319, 1523–1526.
2. N. Mizuno, U. Baxa and A. C. Steven, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 3252–3257.
3. M. L. DeMarco and V. Daggett, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 2293–2298.
4. D. O. V. Alonso, S. J. DeArmond, F. E. Cohen and V. Daggett, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 2985–2989.
5. G. Yoon, Y. Kab Kim, K. Eom and S. Na, Appl. Phys. Lett., 2013, 102, 011914.
6. A. O. Samson and M. Levitt, Biochemistry, 2011, 50, 2243–2248.
7. G.-P. Zhou and R.-B. Huang, Curr. Top. Med. Chem., 2013, 13, 1152–1163.
8. F. Chiti and C. M. Dobson, Annu. Rev. Biochem., 2006, 75, 333–366.
9. T. Haliloglu, I. Bahar and B. Erman, Phys. Rev. Lett., 1997, 79, 3090.
10. I. Bahar and A. J. Rader, Curr. Opin. Struct. Biol., 2005, 15, 586–592.
11. I. Bahar, T. R. Lezon, L.-W. Yang and E. Eyal, Annu. Rev. Biophys., 2010, 39, 23–42.
12. M. A. Deriu, M. Soncini, M. Orsi, M. Patel, J. W. Essex, F. M. Montevecchi and A. Redaelli, Biophys. J., 2010, 99, 2190–2199.
13. Z. Xu, R. Paparcone and M. J. Buehler, Biophys. J., 2010, 98, 2053–2062.
14. G. Yoon, J. Kwak, J. I. Kim, S. Na and K. Eom, Adv. Funct. Mater., 2011, 21, 3454–3463.
15. L. Yang, G. Song and R. L. Jernigan, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 12347–12352.
16. H. Van Melckebeke, C. Wasmer, A. Lange, E. Ab, A. Loquet, A. Böckmann and B. H. Meier, J. Am. Chem. Soc., 2010, 132, 13765–13775.
17. M. M. Tirion, Phys. Rev. Lett., 1996, 77, 1905.
18. A. R. Atilgan, S. R. Durell, R. L. Jernigan, M. C. Demirel, O. Keskin and I. Bahar, Biophys. J., 2001, 80, 505–515.
19. A. Kis, S. Kasas, B. Babić, A. J. Kulik, W. Benoît, G. A. D. Briggs, C. Schönenberger, S. Catsicas and L. Forró, Phys. Rev. Lett., 2002, 89, 248101.
20. L. Yang, G. Song and R. L. Jernigan, Biophys. J., 2007, 93, 920–929.
21. T. P. Knowles, A. W. Fitzpatrick, S. Meehan, H. R. Mott, M. Vendruscolo, C. M. Dobson and M. E. Welland, Science, 2007, 318, 1900–1903.
22. R. I. Dima and H. Joshi, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 15743–15748.
23. H. Zhou, E. Liang, X. Ding, Z. Zheng and Y. Peng, Chem. Commun., 2012, 48, 10553–10555.
24. H. Zhou, X. Ding, Z. Zheng and Y. Peng, Soft Matter, 2013, 9, 4956–4968.
25. J. N. S. P. G. Timoshenko, Theory of elasticity, Mc Graw Hill, 1970.
26. J. M. G. S. Timoshenko, Mechanics of Materials, Brooks/Cole Engineering Division, 1984.
27. L. Meirovitch, Fundamentals of Vibrations, McGraw Hill, 2001.
28. S. Jiang, H. Zhang, Y. Zheng and Z. Chen, J. Phys. D: Appl. Phys., 2009, 42, 135408.

---

Footnote

† Electronic supplementary information (ESI) available: The details of structural information of the HET-s triplet nanofibrils, and theoretical methods are presented in supporting materials. See DOI: 10.1039/c5ra08015k

---