Mechanism and stereoselectivity of the Rh(II)-catalyzed cyclopropanation of diazooxindole: a density functional theory study

Abstract

The mechanism and origin of stereoselectivity of rhodium(II)-catalyzed cyclopropanation reactions with diazooxindole and styrene has been studied using density functional theory calculations. The catalyzed reactions by achiral Rh₂(OAc)₄ and chiral Rh₂(S-PTTL)₄ as well as the uncatalyzed model were comparatively studied. The computational results indicate that the cyclopropanation step in both Rh₂(OAc)₄ and Rh₂(S-PTTL)₄ models is a single concerted but asynchronous process. The nitrogen extrusion step is found to be the rate-limiting step of the catalytic cycle, whereas the cyclopropanation step is the stereoselectivity-determining step. The diastereomeric ratios (dr) and the enantiomeric excess (ee) values are successfully predicted, which are in good agreement with the experimental values. The high trans-diastereoselectivity might be governed by the π–π interactions between the syn indole ring in carbenoid ligand and the phenyl group in styrene, whereas the good enantioselectivity can be ascribed to the steric interaction between the phenyl ring in styrene and the phthalimido group in the catalyst as well as the aromatic interactions (π–π and CH–π) in the transition states. Additionally, the methodological study using different functionals demonstrated the importance of considering the dispersion interactions in the current reaction systems. This theoretical study will help in understanding the mechanism of the asymmetric cyclopropanations of olefins through carbene-transfer reactions.

---

1 Introduction

Spirocyclic oxindole is a privileged structural motif that exists in a large number of natural and synthetic compounds exhibiting biological and pharmaceutical activities.^1–4 Therefore, spirocyclic oxindole scaffolds have continued to draw attention in recent years. Among the spirocyclic oxindoles, 3-spirocyclopropane-2-oxindoles represent an important class that has shown remarkable biological activities and emerged recently as potent drug candidates.^5–7 As a result, great efforts have been directed toward asymmetric construction of these scaffolds.^8–12

Since the pioneering work of Nozaki and Noyori,¹³ the transition metal-catalyzed asymmetric cyclopropanation between diazo compounds and alkenes has emerged as a powerful strategy for the synthesis of cyclopropane derivatives.^14–20 Among the various transition-metal catalysts used, rhodium(II) catalysts bearing carboxylate ligands are one of the most extensively studied and employed catalysts in cyclopropanation reactions.^14,21,22

Among the Rh(II)-carboxylate catalysts, Rh₂(S-PTTL)₄ (dirhodium(II)tetrakis[N-phthaloyl-(S)-tert-leucinate]) is a distinguished example. Rh₂(S-PTTL)₄ was firstly developed by Hashimoto group²³ and has proven to be one of the most universally efficient catalysts for a series of asymmetric reactions, including intramolecular C–H insertions,^24,25 intermolecular 1,3-dipolar cycloadditions via the generation of ester-carbonyl ylides,^26,27 2,3-sigmatropic rearrangements,²⁸ amination²⁸ as well as cyclopropanation.²⁹

Recently, Arai and Awata reported the first enantioselective access to spiro-cyclopropyloxindoles via Rh₂(S-PTTL)₄ catalytic asymmetric cyclopropanation using alkene and diazooxindole (Scheme 1).³⁰ The reaction proceeded smoothly with 1 mol% catalyst loading to provide a good yield with moderate to good enantioselectivity and excellent trans-diastereoselectivity.

Scheme 1 Rh₂(S-PTTL)₄ catalyzed cyclopropanation of styrene and diazooxindole.

As we know, controls of enantioselectivity and/or diastereoselectivity are the key issues in catalytic asymmetric synthesis. To help improve the catalytic system, many experimental^29,31–39 and theoretical studies^40–47 have been carried out to elucidate the reaction mechanism of Rh(II)-carboxylate catalyzed asymmetric cyclopropanation. These mechanistic studies reveal that the Rh(II)-catalytic cycle consists of two main steps, rhodium carbenoid formation and subsequent trapping by olefin (Scheme 2).

Scheme 2 Proposed catalytic cycle for the asymmetric cyclopropanation.

Although general agreement on the mechanism of metal carbenoid formation is reached, there are still debates on the details of the conversion of carbenoid to the product. Davies et al. initially proposed a [2 + 1] pathway initiated by a “side on” approach of alkene to the metal carbene to explain the stereochemical outcome.³⁵ Subsequently, Singleton et al. suggested an “end on” approaching mode.⁴¹ In addition, Corey and co-workers^48,49 suggested a [2 + 2] cycloaddition of alkene with a tribridged metal carbenoid, which now has been largely disregarded in dirhodium(II) catalysis.⁵⁰

Most previous mechanistic studies employed simplified, achiral catalyst model, such as dirhodium(II) tetraformate Rh₂(O₂CH)₄ or dirhodium(II) tetraacetate Rh₂(OAc)₄.^{40–42,45,46} Although results from these models do provide some preliminary insights into the catalyst selectivity, chiral catalyst models based on the “real-world” catalysts are required to better understand the role of the chiral catalysts and the detail reaction process. Indeed, recent studies have demonstrated the importance of considering interactions between the Rh-complex and carbene, as well as the conformational mobility of the ligand in these systems.^29,51

In recent years, computational chemistry, especially density functional theory (DFT) methods have been successfully applied to the mechanistic studies on the transition-metal mediated cyclopropanation reactions.^52–69 However, to the best of our knowledge, no theoretical study on the Rh₂(S-PTTL)₄-catalyzed cyclopropanation of diazooxindoles has ever been reported. Thus, we conducted a computational study on the cyclopropanation between diazooxindoles and styrene to shed light on the catalytic mechanism and the origin of the stereoselectivity. To reveal the catalytic mechanism better, comparative calculations on uncatalyzed and achiral catalyst-catalyzed cyclopropanation reactions have also been performed.

2 Computational details

All calculations have been performed with Gaussian 09 software package.⁷⁰ Molecular geometries were optimized without constraints at the B3LYP^71–73 level of theory in gas phase. The effective core potential (ECP) of Lanl2DZ^74,75 was used to describe Rh, whereas the 6-31G(d) basis set⁷⁶ was used for all the other atoms. The harmonic vibrational frequency calculations at the same level have been carried out to confirm all the stationary points as minima or transition states. The combination of the functional and the basis sets was shown to give reliable results for other rhodium(II) carbenoids.^29,40,41,45 The connectivity between the transition structures and the related reactants and products was confirmed by intrinsic reaction coordinate (IRC)⁷⁷ calculations.

To improve energetic properties, single-point calculations were conducted using larger basis sets 6-311+G(d,p) for H, C, N, and O atoms. The solvent effects (CH₂Cl₂) were considered by using the SMD⁷⁸ solvation model, with single-point calculations based on the gas-phase optimized geometries. The energies discussed in the text are Gibbs free energies calculated at 298.15 K unless otherwise stated.

Recently, there was increasing awareness of the importance of dispersion interactions in organometal mediated homogeneous catalysis.^79–82 In order to investigate the influence of dispersive forces, the empirical dispersion correction of Grimme⁸³ was used in single-point calculations (denoted as D3-B3LYP). For comparison, the M06 ⁸⁴ and wB97XD⁸⁵ functionals with empirical correction of dispersion interactions were also evaluated (Table S1 in ESI†). Our results showed that D3-B3LYP, M06 and wB97XD methods with dispersion correction gave the qualitatively similar results with each other, while the B3LYP method without dispersion correction presented quite different energy values from them. The dispersion correction has little influence on the barrier energy of the N₂ extrusion step, while significant effect on the cyclopropanation step was observed. More importantly, it is somewhat surprising to find that the B3LYP method was not able to predict the correct, even qualitatively, results regarding the rate-determining step in the catalytic cycle. This indicates that dispersion-including methods are needed to describe the styrene addition step more correctly. Considering the consistency and efficiency, the D3-B3LYP method was chosen for following study and the corresponding results were discussed.

Natural bond orbital (NBO)^86,87 analysis was performed at the same level as the one used for geometry optimization. All charge distribution analysis discussed in this article are made on the basis of the natural population analysis (NPA) in solvent. 3D representations of the most significant structures have been created by using CYLView.⁸⁸

3 Results and discussion

3.1 Uncatalyzed model

We first study the uncatalyzed reaction for comparison. The cyclopropanation between diazooxindole (1) and styrene (2) in the absence of catalysts is a single concerted step, in which the cyclopropanation and the extrusion of a N₂ molecule from diazo take place simultaneously, affording the 3-spirocyclopropane-2-oxindole product. The reaction proceeds through nucleophilic attack from the olefinic carbons (C² and C³) of styrene on the carbon atom (C¹) attached to dinitrogen of diazooxindole (Fig. 1). The distances of C¹–C² and C¹–C³ are not equal in the transition state (TS), indicating that this process is nonsynchronous. Since diazooxindole is planar, two faces (Re and Si) are available for styrene to approach. For each face, styrene can attack along two different approaching trajectories (trans or cis), which lead to four isomeric products including (S,R)-trans, (R,S)-trans, (S,S)-cis, and (R,R)-cis. Correspondingly there are four isomeric TSs which are pairs of trans- or cis-adducts, each being, in turn, a pair of enantiomers. As expected, no notable difference in either barrier or geometry was found between two trans or cis isomeric transition states. Here we only discuss the Si-face results. The Re-face results were given in Fig. S1 in ESI.† The calculated Gibbs free energy barriers are 41.7 and 42.4 kcal mol⁻¹ for the trans and cis pathways, respectively (Fig. 1). Clearly, the trans pathway is favored by 0.7 kcal mol⁻¹ over the cis pathway, which accounts for the higher trans selectivity than that of cis isomer. As shown in Fig. 1, there is little difference in the structural parameters between the trans- and cis-isomeric TSs.

Fig. 1 Energy profile for the uncatalyzed cyclopropanation of diazooxindole and styrene for the Si-face pathway.

3.2 Achiral Rh₂(OAc)₄ model

Rh₂(OAc)₄ (3), the parent compound of the dirhodium carboxylates, is a simplified and reasonable model used in mechanistic study to mimic rhodium carboxylates. Previously, Rh₂(OAc)₄ was also used as catalyst in the racemic version of the cyclopropanation reaction reported by Arai and Awata.³⁰ Therefore, we investigate the Rh₂(OAc)₄ catalyzed cyclopropanation reaction of diazooxindole and styrene.

Rh₂(OAc)₄ has D_4h symmetry, which is the highest obtainable symmetry for dirhodium paddlewheel complexes.²¹ Our calculated structural parameters are in nice accordance with those of X-ray (see Fig. S2 in ESI†).⁸⁹ This further indicates that the method employed in this study is suitable for the studied systems.

3.2.1 Formation of Rh(II) carbenoid. The first step in the catalytic cycle is complexation of diazooxindole 1 to the catalyst 3. Rh₂(OAc)₄ has two facile axial coordinate sites, both or either of which can be occupied by substrate molecules. Previous experimental studies^90,91 have proved that carbene bonding occurs only at one coordinate site at a time. Therefore, we only considered the case in which only one site is occupied. Three possible coordination modes of 1 to 3 are conceivable, depending on the atom bonding to the catalyst, via the carbene carbon atom (4, Fig. S3 in ESI†), the terminal diazo nitrogen (5) or the carbonyl oxygen (6).^41,45,81 Besides diazooxindole, styrene may also coordinate with the catalyst. Fig. S3† displays the located complexes via different coordination site between Rh₂(OAc)₄ and styrene, 7 and 8.

As can be seen from Fig. S3,† complex 6 is most stable, indicating that 1 tends to bond to 3 through its O atom. Complex 4 is less favorable than 6 by 4.0 kcal mol⁻¹. For the two complexes of 3 with styrene 2, 7 and 8, both of them are energetically unfavorable with respect to the isolated 2 and 3 by more than 2.8 kcal mol⁻¹, though 7 in which styrene is coordinated via the alkene moiety is slightly more stable than 8. These data suggest that catalyst 3 prefers to coordinate with diazooxindole 1 via the carbonyl oxygen to afford complex 6. Although complex 6 is the most favorable one among the possible complexes, only complex 4 is presumed to be the product-forming complex.^41,45,81 Thus, 6 is expected to first isomerize to 4 with a 4.0 kcal mol⁻¹ free energy increase before it reacts with 2. A similar process is shown likely by Houk et al.⁹²

Fig. 2 presents the potential energy profile for the Rh₂(OAc)₄ catalyzed cyclopropanation of diazooxindole starting from the complex 4 whose formation from 1 and 3 is predicted to be weak endergonic by 3.4 kcal mol⁻¹. Subsequently, the rhodium–diazooxindole complex 4 has to overcome a potential free energy barrier of 15.5 kcal mol⁻¹ (TS9) for nitrogen extrusion to form the rhodium carbenoid intermediate 10. This process is exergonic by 7.7 kcal mol⁻¹ relative to the free reactants (1, 2, and 3). The calculated activation enthalpy (ΔH^‡₂₉₈) for N₂ extrusion (15.3 kcal mol⁻¹) is close to the experimental value (ΔH^‡ = 15.0 kcal mol⁻¹) for carbenoid generation from 3 and ethyl diazoacetate.⁹³ Similar values were also found in previous theoretical studies on the reaction models of methyl diazoacetate (ΔH^‡ = 15.3 kcal mol⁻¹;⁴¹ ΔE^‡ = 11.9 kcal mol⁻¹)⁴² or ethyl diazoacetate (ΔH^‡ = 14.8 kcal mol⁻¹)⁴⁵ with Rh₂(O₂CH)₄.

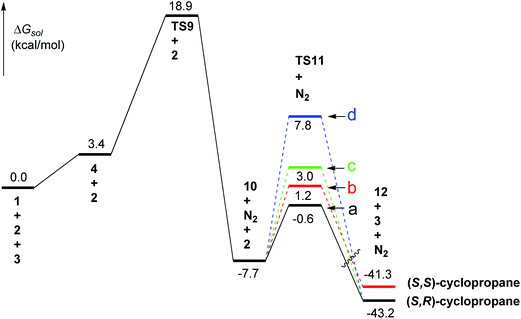Fig. 2 Free energy profile for the Rh₂(OAc)₄ catalyzed cyclopropanation of diazooxindole and styrene.

Pirrung et al.⁹¹ demonstrated that the reversible formation of some alternative complexes between the substrate and the catalyst, even if they are nonproductive bystanders, will affect the reaction rate by lowering the overall initial energy of the system. In this sense, the free energy barrier for extrusion of N₂ would be 19.5 kcal mol⁻¹, the energy difference between the most stable complex 6 and TS9.

As can be seen from Fig. 3, the C¹–N bond is lengthened from 1.30 in 1 to 1.33 Å in 4 upon the complexation between 1 and 3. Concomitantly the Rh¹–Rh² distance extends from 2.39 to 2.41 Å, implying weakening of Rh–Rh bonding. With the strengthening of Rh¹–C¹ bonding, as shown by significant shortening of Rh¹–C¹ bond from 2.48 in 4 to 2.10 Å in TS9, C¹–N bond is further elongated from 1.33 to 1.80 Å in TS9, and Rh¹–Rh² stretches to 2.45 Å (TS9). In N₂ extrusion product 10 the Rh¹–C¹ bond further decreases to 1.97 Å while Rh¹–Rh² extends slightly to 2.46 Å. The variation of Rh¹–C¹ and Rh¹–Rh² bond lengths shows that TS9 possesses more character of the carbenoid complex 10. As shown in Fig. 3 and S4,† the carbenoid would preferentially line up staggered to the carboxylate ligands of the catalyst to avoid steric repulsion between the bulky phenyl group in diazooxindole and the carboxylate ligand. Moreover, a staggered arrangement is required for stabilization of the carbenoid ligand by metal back-bonding.^35,42

Fig. 3 Calculated structures (side view) of the stationary points involved in the Rh₂(OAc)₄ catalyzed cyclopropanation. Values in parentheses are bond orders.

3.2.2 Cyclopropanation. The following step in the catalytic cycle is the cyclopropanation reaction between the formed carbenoid 10 and styrene 2. This reaction takes place in a single step, as verified by our intrinsic reaction coordinate (IRC) calculations. Since Rh₂(OAc)₄ catalyst is symmetric, the two faces of metal carbene are homotopic, and therefore styrene can equally attack metal carbene through either Re or Si face. Herein only Si-face results are given and discussed below.

Styrene can access the carbenoid complex through either an end-on trajectory (the alkene parallel to the Rh–C bond), or a side-on trajectory (the alkene perpendicular to the Rh–C bond). For each trajectory, styrene may approach in four different orientations depending on the position of the phenyl group in styrene with respected to the carbonyl group (cis or trans) and the catalyst (endo or exo). Four transition states end-on/trans/exo (TS11-a), end-on/cis/exo (TS11-b), side-on/cis/exo (TS11-c), and side-on/trans/endo (TS11-d) were successfully located (Fig. 3). The predicted Rh–C–C=C dihedral angles are −174.4°, 173.4°, 96.8° and −97.3° for the four transition states, respectively. All our efforts to locate the endo transition structures for TS11-a, TS11-b and TS11-c were unsuccessful, due to the styrene rotation upon optimization around the C¹–C² bond to afford an exo orientation (for more details, see ESI†). Similar phenomenon has also been observed in previous study on Au-catalyzed cyclopropanation.⁶¹

Among the four located TSs, only TS11-d adopts the endo-mode, the others adopt the exo-mode. The minority of endo-mode is not unexpected because it is unfavored relative to the exo-mode due to the steric hindrance between the phenyl group in styrene and the ligands in catalyst, especially for the end-on trajectory. Indeed, the TS11-d was too high in energy to be of importance as discussed in following text.

As shown in Fig. 2, the end-on transition state TS11-a and the side-on transition states TS11-c and TS11-d, leading to the trans-substituted cyclopropane (12a), are calculated to have free energy barriers of 7.1 (a), 10.7 (c) and 15.5 (d) kcal mol⁻¹; whereas the end-on transition state TS11-b leading to the cis-substituted cyclopropane (12b), represents a barrier of 8.9 kcal mol⁻¹. Among these four TSs, the side-on TS11-d is not of importance because of its significantly high barrier (15.5 kcal mol⁻¹). Clearly, the end-on approaching of the styrene is favored over the side-on trajectory. Taking the three favored transition states into account and using the Boltzmann equation, we calculated the trans/cis ratio to be 95.4 : 4.6, which is in very good agreement with the experimental value (95 : 5).³⁰

The whole process is highly exergonic, with predicted energy lowering of 41.3 and 43.2 kcal mol⁻¹ respectively with respect to the free reactants (Fig. 2). The final product is more than 30 kcal mol⁻¹ more stable than the carbenoid complex 10. Clearly, the nitrogen extrusion from complex 4 is the rate-limiting step of the catalytic cycle.

Of the two end-on transition states TS11-a and TS11-b, the former that produces trans-product is the more favorable. It can be seen from the NBO results (Table S3 in ESI†) that the interactions between carbene complex and styrene in both TS11-a and TS11-b are mainly from π(C46–C48) → LP*C39 and LP*C39 → π*(C46–C48). The corresponding second order perturbation stabilization energy E(2) of TS11a are larger than that of TS11b. In addition, the aromatic interactions (π–π) between syn indole ring in carbenoid ligand and styrene are also contribute to the stabilization of the TSs, especially for the trans one (TS11a). These differences may be responsible for the favorability of TS11a than TS11b, resulting in an excess of the trans-diastereomeric cyclopropane. Our further calculations shown that when the phenyl group in styrene was substituted by n-C₃H₇, the value of ΔΔG^‡ decreased from 1.8 to 1.4 kcal mol⁻¹, and as a result, the diastereoselectivity (dr) decreased due to the disappearance of the π–π interactions. This is in agreement with the experimental observations,³⁰ which further confirmed the important role of the dispersion interactions in stereocontrol.^61,79,82,94

Contrary to D3-B3LYP, the B3LYP computations provided a smaller difference in free-energy barriers ΔΔG^‡ (only 0.5 kcal mol⁻¹) and predict a lower trans/cis ratio (72 : 28) for styrene, in poor agreement with experimental result (95 : 5). It is understandable if we take into account that the noncovalent interactions involved in cyclopropanation step influence the diastereoselectivity and that the B3LYP functional is incapable of providing an accurate and reliable description of noncovalent (especially dispersion) interactions. Clearly, the incorporation of nonlocal dispersion effects is crucial to achieve a reasonable agreement between theory and experiment.

As can be seen from Fig. 3, upon styrene approach, the carbene will bend (the two Rh atoms are no longer co-planar with the carbenoid) and C¹ possesses more sp³-hybridiztion character. In TS11, there are no significant changes in the length of Rh¹–Rh² bonds with respect to 10. However, and Rh¹–C¹ is lengthened by more than 0.08 Å. The geometrical parameters of the core structure of the four TS11 are very similar with each other. Like the un-catalyzed reaction, the cyclopropanation step in Rh₂(OAc)₄ model is also concerted but asynchronous as evidenced by the large difference between the distances of C¹–C² and C¹–C³. C¹–C² bond forms slightly ahead of C¹–C³ bond. The C¹–C² and C¹–C³ bond orders in all four transition states are less than 0.4, indicative of early, reactant-like transition states for the cyclopropanation step. In addition, the two end-on transition states (TS11-a and TS11-b) show more early transition state character than the two side-on TSs (TS11-c and TS11-d).

The natural population analysis (NPA, Table S4 in ESI†) shows that the carbenoid moiety in the carbenoid complex 10 has a positive charge of +0.33, indicating that complex 10 is an electrophilic carbenoid, and this is further confirmed by the analysis of the LUMO orbital of the complex 10 (Fig. S5 in ESI†). As depicted in Fig. S5,† LUMO of complex 10 was composed mainly of the carbene carbon 2p_z orbital, which accepts rather small back-donation from the Rh¹ 4d_xz orbital to form an extended π*-system that possesses a strongly electrophilic carbene carbon. The carboxylate groups in 10 are less negatively charged (−1.31) as compared to that of catalyst 3 (−1.42), which is likely induced by the back-donation from the Rh¹ atom to the carbenoid moiety. By comparison, the charge on the Rh¹ atom changes little during the carbene complex formation (+0.51 → +0.47).

3.3 Chiral Rh₂(S-PTTL)₄ model

The above results obtained with the achiral Rh₂(OAc)₄ model present valuable information about the general mechanism of the Rh(II)-carboxylate catalyzed cyclopropanation reaction of diazooxindoles. However, the simplicity of the model precludes a detailed insight into the origin of the stereoselectivity, especially the enantioselectivity. Therefore, to further probe the reaction mechanism and the effect of the ligand in catalysts on the stereoselectivity, the chiral Rh₂(S-PTTL)₄ model was employed.

Recently, Fox and co-workers reported the X-ray crystal structure of the Rh₂(S-PTTL)₄.²⁹ Their results revealed that Rh₂(S-PTTL)₄ adopts a C₄-symmetry-like “chiral crown” conformation, in which all four N-phthalimide groups are located on one face, and the four tert-butyl groups are oriented on the opposite face. This chiral crown structure was supported by themselves and other research groups in subsequent investigations on other phthalimido-derived catalysts.^95–98 According to this model, the reactive chiral face consisting of the chiral crown-like ligands in Rh₂(S-PTTL)₄ guides the facial selectivity and the four bulky tert-butyl groups limit the reactivity of the achiral face of the catalyst.

Based on the X-ray structure of Rh₂(S-PTTL)₄, the cavity formed by four N-phthalimide groups has a wide (∼15 Å) and narrow dimension (∼11 Å). This unique structure will affect the alignment of carbene in the cavity of the catalyst and the catalytical behavior as shown in Fox's study.²⁹ Recent investigations by other groups supported the importance of the steric environment within the catalyst.^51,97 As such, we first explored the coordination of diazooxindole with Rh₂(S-PTTL)₄. All together, we have located twelve distinct minima on the potential energy surfaces corresponding to different conformations of the diazooxindole with Rh₂(S-PTTL)₄ (see ESI†). The lowest energy conformation is depicted in Fig. S6 in ESI.† Our calculations indicate that the oxindole group orients itself away to avoid the steric repulsion with the phthalimido walls. Thus diazooxindole is preferentially aligned with the wide dimension of the chiral cavity (14, Fig. S6†). Similar to the Rh₂(OAc)₄ model, the carbenoid would preferentially line up staggered to the carboxylate ligands and aligned with the wide dimension of the chiral cavity (16, Fig. S6†). This is similar with the Fox's results using α-alkyl-α-diazoester as carbene precursor.²⁹

Similar to the Rh₂(OAc)₄ model, in Rh₂(S-PTTL)₄ system, styrene can also attack carbenoid 16 through either Re or Si faces; and in each face, two trajectories (end-on and side-on) are possible. However, in this case, the two faces (Re and Si) are no longer equivalent due to the chiral environment of the Rh₂(S-PTTL)₄ catalyst. As can be seen from Fig. 4, three transition states including two end-on (TS17-a and TS17-d) and one side-on (TS17-e) were located for the Si-face, while two end-on transition state (TS17-b and TS17-c) was found for Re-face. TS17-a, TS17-d and TS17-e correspond to the TS11-a, TS11-b and TS11-c, respectively. The side-on transition state, congener of TS11-d that adopts the endo-mode, was not located due to the severe steric repulsion between the phenyl group in styrene and the catalyst. Considering that TS11-d does not contribute much in the Rh₂(OAc)₄-catalyzed process, the absence of the congener in Rh₂(S-PTTL)₄ catalyzed cyclopropanation should not exert noticeable influence either. For the case of Re-face, we were not able to locate the side-on transition state similar to TS17-e due to the large steric repulsion between the phenyl group and the phthalimido ligand.

Fig. 4 Optimized structures of the stationary points involved in the Rh₂(S-PTTL)₄ catalyzed cyclopropanation.

By comparison, it was found that the key geometrical parameters of the structures in the reaction pathway for Rh₂(S-PTTL)₄ are very similar to the analogous structures for Rh₂(OAc)₄. As shown in Fig. 4, the cyclopropanation step in the Rh₂(S-PTTL)₄ system is also concerted but highly asynchronous as evidenced by the distances and bond orders of C¹–C² and C¹–C³. Moreover, the end-on transition states (TS17-a, TS17-b, TS17-c and TS17-d) are slightly early than the side-on TS (TS17-e).

Fig. 5 shows the potential energy profile for the Rh₂(S-PTTL)₄ catalyzed cyclopropanation of diazooxindole and styrene. The initial complexation of diazooxindole 1 with the catalyst 13 is predicted to be exergonic by 5.6 kcal mol⁻¹. Then loss of the N₂ from 14 via TS15 has a free energy barrier of 13.9 kcal mol⁻¹. The generated carbenoid intermediate 16 is stabilized relative to the free reactants (1, 2, and 13) by −14.8 kcal mol⁻¹. Compared to the Rh₂(OAc)₄ model, the calculated activation enthalpy of N₂ extrusion (ΔH^‡₂₉₈ = 14.6 kcal mol⁻¹) decreases slightly and is also close to the experimental value (ΔH^‡ = 15.0 kcal mol⁻¹).⁹³

Fig. 5 Free energy profile for the Rh₂(S-PTTL)₄ catalyzed cyclopropanation of diazooxindole and styrene.

In the case of Si-face, the end-on transition state TS17-a yielding the trans product is 2.2 kcal mol⁻¹ lower in energy than the end-on transition state TS17-d that leads to the cis product. This difference is 0.4 kcal mol⁻¹ larger than that of Rh₂(OAc)₄ model (1.8 kcal mol⁻¹). Thus Rh₂(S-PTTL)₄ exhibits higher diastereoselectivity than achiral Rh₂(OAc)₄. With the four main TSs, we calculated a trans/cis ratio of 97.3 : 2.7, which is in very good agreement with the experimental value (97 : 3). The side-on transition state TS17-e producing the trans isomer is predicted to have a barrier of 5.3 kcal mol⁻¹, significantly higher than those of the others, and thus its contribution is trivial.

It was observed that the barrier of Re-trans path (TS17-b) is 2.0 kcal mol⁻¹, higher than that of Si-trans path (TS17-a) by 0.6 kcal mol⁻¹. This means Si-face attack is favored over the Re-face, which accounts for the enantioselectivity of the reaction. With the barriers, the ee value was predicted to be of 50.3%, which is reasonably close to the experimental value of 66%.

It can be observed from Fig. 5 that formation of carbenoid 16 presents the highest barrier in the catalytic cycle and therefore is the rate-determining step. This is in line with the case of Rh₂(OAc)₄. In addition, the cyclopropanation process is thermodynamically very favorable (−41.3 to −43.2 kcal mol⁻¹), in agreement with the irreversible character of cyclopropanation reactions.

In an effort to gain some insights into the origin of the stereoselectivity observed, we examined the calculated TS structures (Fig. 6). As shown in Fig. 6a, π–π interaction between the syn indole ring in carbenoid ligand and the phenyl group in styrene might happen in TS17-a, while this interaction is lacking in TS17-d (Fig. 6c). The stabilising π–π interaction would stabilize TS17-a, resulting in an excess of the trans-diastereomeric cyclopropane.

Fig. 6 Factors control the stereoselectivity in the Rh₂(S-PTTL)₄ catalyzed cyclopropanation of diazooxindole. Three key transition states TS17-a (a), TS17-b (b) and TS17-d (c) are presented and the key nonbonding interactions (in Å) are indicated.

As far as the enantioselectivity is concerned, the unfavorability of Re-face attack might due to the steric repulsion between the phenyl group in styrene and the phthalimido ligand in catalyst (Fig. 6b). Meanwhile, the π–π interaction might happen in the Si-face attack mode between the carbenoid ligand and the phthalimido group in the catalyst, which will promote the stability of Si-face TS (TS17-a, Fig. 6a). Moreover, TS17-a also possesses relatively strong CH–π interactions between phenyl hydrogen and the phthalimido group (interaction distances of 3.28–3.48 Å), which further stabilize TS17-a. On the contrary, the π–π interaction between the carbenoid ligand and the phthalimido group is lacking in the Re-face attack model (TS17-b). Although the CH–π interactions are still present in TS17-b, they are very weak due to the large distances and the less ideal alignment. To sum up, the two factors, steric repulsion and aromatic interactions (π–π and CH–π), are responsible for the good enantioselectivity.

Compared with the Rh₂(OAc)₄ model, Rh₂(S-PTTL)₄ reduces the barriers of the cyclopropanation step significantly, as shown by the barriers of 1.4 (TS17-a), 3.6 (TS17-d) and 5.4 (TS17-e) kcal mol⁻¹ which are more than 5 kcal mol⁻¹ lower than the corresponding barriers with the Rh₂(OAc)₄-system, 7.1, 8.9 and 10.7 kcal mol⁻¹. This may be explained by the enhancement of the eletrophilicity of carbenoid complex 16. According to the NPA analysis (Table S5 in ESI†), the carbenoid moiety in carbenoid complex 16 has a positive charge of +0.36, suggesting an electrophilic carbenoid as supported by the LUMO orbital diagram (Fig. 7). By comparison, the charge on the carbenoid moiety in 16 is larger than that of complex 10. On the other hand, the energy of LUMO of 16 (−3.83 eV) is lower than that of 10 (−3.77 eV), indicating that carbenoid complex 16 has stronger eletrophilicity than 10. This might account for the decrease of the barriers of cyclopropanation step in the Rh₂(S-PTTL)₄ system.

Fig. 7 Diagram of LUMO of carbenoid complex 16.

4 Conclusions

In this paper, we have presented a detail computational study on the mechanism of Rh(II)-catalyzed cyclopropanation reactions between diazooxindole and styrene to gain insight into the origin of the stereoselectivity. Density functional theory at the SMD-(D3) B3LYP/6-311+G**-Lanl2DZ//B3LYP/6-31G*-Lanl2DZ level was used for the investigations. In the absence of the catalyst, the cyclopropanation between diazooxindole and styrene is a single concerted step, with very high barrier of 42.4 and 41.7 kcal mol⁻¹ for the cis and trans pathway, respectively. The catalyzed reaction proceeds through a stepwise process including the formation of carbene species and a cyclopropanation step to provide the cyclopropane product and regenerate the catalyst. The rate-determining step of the catalytic cycle was found to be the formation of a Rh(II) carbenoid, representing a barrier of 15.5 and 13.9 kcal mol⁻¹ for Rh₂(OAc)₄ and Rh₂(S-PTTL)₄, respectively. The computational results show that styrene can approach to the carbenoid complex through the end-on or side-on trajectory, and the former is more favorable than the latter. The predicted diastereomeric ratio (trans/cis) and the enantiomeric excess (ee) values are in good agreement with the experimental values. The present calculations indicate that the nonbonding interactions play an important role in determining the stereoselectivity. The origin of the high trans-diastereoselectivity lies in the π–π interactions between the syn indole ring in carbenoid ligand and the phenyl group in styrene, whereas the good enantioselectivity can be ascribed to steric interaction between the phenyl ring in styrene and the phthalimido ligand in catalyst as well as the stabilizing π–π and CH–π interactions in transition states. In addition, the methodological studies using different functionals demonstrated the importance of inclusion of dispersion correction to correctly elucidate the reaction mechanism. These results provide valuable information about the origin of the stereoselectivity, which might be useful in further developments of the Rh(II)-catalyzed cyclopropanations.

Acknowledgements

The authors acknowledge the financial support from the National Key Basic Research Development Program of China (973 Program) 2011CB808604, and the Natural Science Foundation of China (no. 20973090 and 21273103). Y.-S. Xue also thanks the financial support from Jiangsu Key Laboratory of New Drug Research and Clinical Pharmacy (ZR-XY201404), the Science and Technology Plan Projects of Xuzhou (XZZD1224), the Priority Academic Program Development of Jiangsu Higher Education Institutions and the Innovative Practice Training Program for Students of Jiangsu Higher Education Institutions (201410313052X).

Notes and references

1. B. Tan, N. R. Candeias and C. F. Barbas, Nat. Chem., 2011, 3, 473–477.
2. T. Mugishima, M. Tsuda, Y. Kasai, H. Ishiyama, E. Fukushi, J. Kawabata, M. Watanabe, K. Akao and J. Kobayashi, J. Org. Chem., 2005, 70, 9430–9435.
3. C. V. Galliford and K. A. Scheidt, Angew. Chem., Int. Ed., 2007, 46, 8748–8758.
4. T. Jiang, K. L. Kuhen, K. Wolff, H. Yin, K. Bieza, J. Caldwell, B. Bursulaya, T. Y. H. Wu and Y. He, Bioorg. Med. Chem. Lett., 2006, 16, 2105–2108.
5. J. R. Bagley, S. A. Thomas, F. G. Rudo, H. K. Spencer, B. M. Doorley, M. H. Ossipov, T. P. Jerussi, M. J. Benvenga and T. Spaulding, J. Med. Chem., 1991, 34, 827–841.
6. T. Jiang, K. L. Kuhen, K. Wolff, H. Yin, K. Bieza, J. Caldwell, B. Bursulaya, T. Tuntland, K. Y. Zhang, D. Karanewsky and Y. He, Bioorg. Med. Chem. Lett., 2006, 16, 2109–2112.
7. D. W. Robertson, J. H. Krushinski, G. D. Pollock, H. Wilson, R. F. Kauffman and J. S. Hayes, J. Med. Chem., 1987, 30, 824–829.
8. X. W. Dou and Y. X. Lu, Chem.–Eur. J., 2012, 18, 8315–8319.
9. A. Noole, N. S. Sucman, M. A. Kabeshov, T. Kanger, F. Z. Macaev and A. V. Malkov, Chem.–Eur. J., 2012, 18, 14929–14933.
10. Z.-Y. Cao, Y.-H. Wang, X.-P. Zeng and J. Zhou, Tetrahedron Lett., 2014, 55, 2571–2584.
11. Z. Y. Cao, F. Zhou, Y. H. Yu and J. Zhou, Org. Lett., 2013, 15, 42–45.
12. Z. Y. Cao, X. Wang, C. Tan, X. L. Zhao, J. Zhou and K. Ding, J. Am. Chem. Soc., 2013, 135, 8197–8200.
13. H. Nozaki, S. Moriuti, H. Takaya and R. Noyori, Tetrahedron Lett., 1966, 5239–5244.
14. M. P. Doyle and D. C. Forbes, Chem. Rev., 1998, 98, 911–935.
15. F. Lopez and J. L. Mascarenas, Beilstein J. Org. Chem., 2013, 9, 2250–2264.
16. G. Bartoli, G. Bencivenni and R. Dalpozzo, Synthesis-Stuttgart, 2014, 46, 979–1029.
17. A. Caballero, A. Prieto, M. M. Díaz-Requejo and P. J. Pérez, Eur. J. Inorg. Chem., 2009, 2009, 1137–1144.
18. J. M. Concellon, H. Rodriguez-Solla, C. Concellon and V. del Amo, Chem. Soc. Rev., 2010, 39, 4103–4113.
19. G. Maas, Chem. Soc. Rev., 2004, 33, 183–190.
20. D. Y. Qian and J. L. Zhang, Chem. Soc. Rev., 2015, 44, 677–698.
21. J. Hansen and H. M. L. Davies, Coord. Chem. Rev., 2008, 252, 545–555.
22. F. G. Adly and A. Ghanem, Chirality, 2014, 26, 692–711.
23. N. Watanabe, T. Ogawa, Y. Ohtake, S. Ikegami and S. Hashimoto, Synlett, 1996, 85–86.
24. K. Minami, H. Saito, H. Tsutsui, H. Nambu, M. Anada and S. Hashimoto, Adv. Synth. Catal., 2005, 347, 1483–1487.
25. H. Saito, H. Oishi, S. Kitagaki, S. Nakamura, M. Anada and S. Hashimoto, Org. Lett., 2002, 4, 3887–3890.
26. N. Shimada, M. Anada, S. Nakamura, H. Nambu, H. Tsutsui and S. Hashimoto, Org. Lett., 2008, 10, 3603–3606.
27. H. Tsutsui, N. Shimada, T. Abe, M. Anada, M. Nakajima, S. Nakamura, H. Nambu and S. Hashimoto, Adv. Synth. Catal., 2007, 349, 521–526.
28. S. Kitagaki, Y. Yanamoto, H. Tsutsui, M. Anada, M. Nakajima and S. Hashimoto, Tetrahedron Lett., 2001, 42, 6361–6364.
29. A. DeAngelis, O. Dmitrenko, G. P. A. Yap and J. M. Fox, J. Am. Chem. Soc., 2009, 131, 7230–7231.
30. A. Awata and T. Arai, Synlett, 2013, 24, 29–32.
31. J. L. Maxwell, K. C. Brown, D. W. Bartley and T. Kodadek, Science, 1992, 256, 1544–1547.
32. M. P. Doyle, Chem. Rev., 1986, 86, 919–939.
33. M. P. Doyle, J. H. Griffin, V. Bagheri and R. L. Dorow, Organometallics, 1984, 3, 53–61.
34. M. P. Doyle, Acc. Chem. Res., 1986, 19, 348–356.
35. H. M. L. Davies, P. R. Bruzinski, D. H. Lake, N. Kong and M. J. Fall, J. Am. Chem. Soc., 1996, 118, 6897–6907.
36. H. B. Wang, D. M. Guptill, A. Varela-Alvarez, D. G. Musaev and H. M. L. Davies, Chem. Sci., 2013, 4, 2844–2850.
37. K. P. Kornecki, J. F. Briones, V. Boyarskikh, F. Fullilove, J. Autschbach, K. E. Schrote, K. M. Lancaster, H. M. L. Davies and J. F. Berry, Science, 2013, 342, 351–354.
38. J. P. Snyder, A. Padwa, T. Stengel, A. J. Arduengo, A. Jockisch and H. J. Kim, J. Am. Chem. Soc., 2001, 123, 11318–11319.
39. V. N. G. Lindsay, C. Nicolas and A. B. Charette, J. Am. Chem. Soc., 2011, 133, 8972–8981.
40. E. Nakamura, N. Yoshikai and M. Yamanaka, J. Am. Chem. Soc., 2002, 124, 7181–7192.
41. D. T. Nowlan, T. M. Gregg, H. M. L. Davies and D. A. Singleton, J. Am. Chem. Soc., 2003, 125, 15902–15911.
42. J. Hansen, J. Autschbach and H. M. L. Davies, J. Org. Chem., 2009, 74, 6555–6563.
43. J. A. S. Howell, Dalton T., 2007, 1104–1114.
44. J. Hansen, B. Li, E. Dikarev, J. Autschbach and H. M. L. Davies, J. Org. Chem., 2009, 74, 6564–6571.
45. H. T. Bonge and T. Hansen, J. Org. Chem., 2010, 75, 2309–2320.
46. H. T. Bonge and T. Hansen, Tetrahedron Lett., 2010, 51, 5298–5301.
47. J. A. S. Howell, Dalton T., 2007, 3798–3803.
48. Y. Lou, M. Horikawa, R. A. Kloster, N. A. Hawryluk and E. J. Corey, J. Am. Chem. Soc., 2004, 126, 8916–8918.
49. Y. Lou, T. P. Remarchuk and E. J. Corey, J. Am. Chem. Soc., 2005, 127, 14223–14230.
50. D. T. Nowlan and D. A. Singleton, J. Am. Chem. Soc., 2005, 127, 6190–6191.
51. C. Qin, V. Boyarskikh, J. H. Hansen, K. I. Hardcastle, D. G. Musaev and H. M. Davies, J. Am. Chem. Soc., 2011, 133, 19198–19204.
52. F. Bernardi, A. Bottoni and G. P. Miscione, Organometallics, 2001, 20, 2751–2758.
53. A. Cornejo, J. M. Fraile, J. I. Garcia, M. J. Gil, V. Martinez-Merino, J. A. Mayoral and L. Salvatella, Organometallics, 2005, 24, 3448–3457.
54. G. Drudis-Sole, F. Maseras, A. Lledos, A. Vallribera and M. Moreno-Manas, Eur. J. Org. Chem., 2008, 5614–5621.
55. J. M. Fraile, J. I. Garcia, V. Martinez-Merino, J. A. Mayoral and L. Salvatella, J. Am. Chem. Soc., 2001, 123, 7616–7625.
56. J. I. Garcia, G. Jimenez-Oses and J. A. Mayoral, Chem.–Eur. J., 2011, 17, 529–539.
57. G. Luo, Y. Luo, S. Maeda, J. P. Qu, Z. M. Hou and K. Ohno, Organometallics, 2014, 33, 3840–3846.
58. T. Rasmussen, J. F. Jensen, N. Ostergaard, D. Tanner, T. Ziegler and P. O. Norrby, Chem.–Eur. J., 2002, 8, 177–184.
59. C. Rodriguez-Garcia, A. Oliva, R. M. Ortuno and V. Branchadell, J. Am. Chem. Soc., 2001, 123, 6157–6163.
60. T. Shi, Y. Luo, X. L. Wang, S. Y. Lu, Y. L. Zhao and J. Zhang, Organometallics, 2014, 33, 3673–3682.
61. E. Soriano and J. Marco-Contelles, Chem.–Eur. J., 2008, 14, 6771–6779.
62. B. F. Straub, I. Gruber, F. Rominger and P. Hofmann, J. Organomet. Chem., 2003, 684, 124–143.
63. A. Fedorov, L. Batiste, A. Bach, D. M. Birney and P. Chen, J. Am. Chem. Soc., 2011, 133, 12162–12171.
64. T. Ikeno, I. Iwakura, S. Yabushita and T. Yamada, Org. Lett., 2002, 4, 517–520.
65. B. F. Straub, J. Am. Chem. Soc., 2002, 124, 14195–14201.
66. M. Buhl, F. Terstegen, F. Loffler, B. Meynhardt, S. Kierse, M. Muller, C. Nather and U. Luning, Eur. J. Org. Chem., 2001, 2151–2160.
67. M. Jaccob and P. Venuvanalingam, Rsc Advances, 2013, 3, 17793–17802.
68. T. Wang, Y. Liang and Z. X. Yu, J. Am. Chem. Soc., 2011, 133, 13762–13763.
69. H. Y. Xu, X. T. Zhang, Z. F. Ke, Z. F. Li, X. Y. Xu, C. Y. Su, D. L. Phillips and C. Y. Zhao, Rsc Advances, 2013, 3, 17131–17142.
70. M. J. T. G. W. Frisch, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, revision D.01, 2013.
71. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
72. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377.
73. C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789.
74. W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284–298.
75. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283.
76. W. J. R. Hehre, L. P. V. R. Schleyer and J. A. Pople, Ab Initio Molecular Orbital Theory, Wiley, New York, 1986.
77. C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527.
78. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
79. E. H. Krenske and K. N. Houk, Acc. Chem. Res., 2013, 46, 979–989.
80. M. Patil, C. Loerbroks and W. Thiel, Org. Lett., 2013, 15, 1682–1685.
81. M. L. Rosenberg, A. Krapp and M. Tilset, Organometallics, 2011, 30, 6562–6571.
82. M. Kumar, R. V. Chaudhari, B. Subramaniam and T. A. Jackson, Organometallics, 2014, 33, 4183–4191.
83. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104–154123.
84. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
85. J. D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
86. A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746.
87. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
88. C. Y. Legault, CYLView 1.0b, Universite de Sherbrooke, Sherbrooke, Quebec, Canada, 2009.
89. F. A. Cotton, B. G. Deboer, M. D. Laprade, J. R. Pipal and D. A. Ucko, Acta. Crystall B-Stru., 1971, 27, 1664–1671.
90. M. C. Pirrung and A. T. Morehead, J. Am. Chem. Soc., 1996, 118, 8162–8163.
91. M. C. Pirrung, H. Liu and A. T. Morehead, J. Am. Chem. Soc., 2002, 124, 1014–1023.
92. Y. Lan and K. N. Houk, J. Org. Chem., 2011, 76, 4905–4909.
93. A. J. Anciaux, A. J. Hubert, A. F. Noels, N. Petiniot and P. Teyssie, J. Org. Chem., 1980, 45, 695–702.
94. E. H. Krenske, Org. Biomol. Chem., 2013, 11, 5226–5232.
95. A. DeAngelis, D. T. Boruta, J. B. Lubin, J. N. Plampin 3rd, G. P. Yap and J. M. Fox, Chem. Commun., 2010, 46, 4541–4543.
96. V. N. G. Lindsay, W. Lin and A. B. Charette, J. Am. Chem. Soc., 2009, 131, 16383–16385.
97. T. Goto, K. Takeda, N. Shimada, H. Nambu, M. Anada, M. Shiro, K. Ando and S. Hashimoto, Angew. Chem., Int. Ed., 2011, 50, 6803–6808.
98. A. Ghanem, M. G. Gardiner, R. M. Williamson and P. Muller, Chem.–Eur. J., 2010, 16, 3291–3295.

---

Footnote

† Electronic supplementary information (ESI) available: Comparison of different DFT methods (Table S1), calculated relative free energies with and without BSSE correction (Table S2), NBO analysis of TS11a and TS11b (Table S3), natural charge analysis (Tables S4 and S5), energy profile for the uncatalyzed cyclopropanation in Re-face pathway (Fig. S1), comparison between the DFT and X-ray structure of Rh₂(OAc)₄ (Fig. S2), and other figures and tables, and xyz file giving the Cartesian coordinates for all structures. See DOI: 10.1039/c5ra07981k

---