Anti-site disorder and physical properties in microwave synthesized RE₂Ti₂O₇ (RE = Gd, Ho) pyrochlores

Abstract

In this work we report on the microwave assisted synthesis of nano-sized Gd₂Ti₂O₇ (GTO) and Ho₂Ti₂O₇ (HTO) powders from the RE₂Ti₂O₇ pyrochlore family (RE = rare earth). Synchrotron X-ray powder diffraction was used to study RE–Ti cationic anti-site defects with concentrations that decrease in both samples with increasing temperature starting from 1100 °C, and the defects disappear at 1400 °C. SQUID magnetometry measurements revealed that GTO shows a predominantly anti-ferromagnetic structure, whereas HTO exhibits magnetic saturation and a ferromagnetic component at low temperature. Impedance spectroscopy data revealed strongly increased ionic oxygen vacancy conduction in HTO ceramic pellets as compared to GTO, which may be associated with a higher degree of oxygen vacancy disorder. This argument was supported by Raman spectroscopy data.

---

1. Introduction

Pyrochlore oxide compounds of the type A₂B₂O₇ are functional materials for a wide range of potential applications due to their high oxygen ion conductivity, dielectric tunability, exotic magnetic properties, multiferroic behaviour and superconductivity.^1–7 Furthermore, due to their high chemical stability and flexibility to form solid solutions with many cations, pyrochlores have been proposed as a host matrix for immobilizing toxic nuclear waste.^8,9

Rare-Earth (RE) titanate pyrochlores have the general formula RE₂Ti₂O₇, where the crystal structure may be regarded a RE³⁺ and Ti⁴⁺ cation ordered superstructure of oxygen deficient fluorite (RE_0.5Ti_0.5O_2-0.25). A concentration of 0.25 oxygen vacancies per formula unit allows ionic oxygen vacancy conduction to occur. The pyrochlore structure (Fig. 1) exhibits an F-centred cubic unit cell with space group (S.G): Fd3̄m (#227) and cell parameter a ≈ 10 Å, which corresponds to approximately the double of the fluorite unit cell parameter.¹⁰ The larger RE³⁺ cations are located on 16d eight-coordinated sites at the centre of scalenohedrons, while Ti⁴⁺ are located on 16c six-coordinated sites at the centre of trigonal antiprisms. The 7 oxygen O²⁻ anions in the chemical formula RE₂Ti₂O₆O′ are located on two different sites: (1) 6 oxygen O(1) on four-coordinated 48f positions with two A cation and two B cation nearest neighbours, and (2) one oxygen O(2) on four-coordinated 8b sites with four A cation nearest neighbours. The third anionic tetrahedral O(3) sites are empty, consisting in four-coordinated 8a sites surrounded by four B cation neighbours. These systematically vacant O(3) sites are characteristic of the ordered pyrochlore structure, in contrast to anion deficient fluorites where anion vacancies are randomly distributed throughout the anion sub-structure. Merely based on steric considerations regarding the cationic radii r, one would expect the eight-coordinated 16d sites in RE₂Ti₂O₇ pyrochlores to be fully occupied by the larger RE³⁺ cations, whereas the smaller Ti⁴⁺ would be located on the six-coordinated 16c positions: r(^VIIIGd³⁺) = 1.053 Å, r(^VIIIHo³⁺) = 1.015 Å and r(^VITi⁴⁺) = 0.605 Å.¹¹ However, in the A₂B₂O₇ pyrochlore structure crystal defects commonly occur, where the two most important ones are (i) cation anti-site, and (ii) anion Frenkel defects. Cation anti-site defects consist in a positional exchange of an A³⁺ (here RE³⁺) with a B⁴⁺ (here Ti⁴⁺) cation, whereas Frenkel anion disorder occurs when a 48f site oxygen anion is displaced to a nominally vacant 8a interstitial site, thus leaving a 48f site unoccupied.^10,12

Fig. 1 Schematic representation of the ideal RE₂Ti₂O₇ pyrochlore structure. Trigonal antiprisms (green) contain the 16c six-coordinated Ti⁴⁺ cations at the centre and the 48f oxygen O(1) at the corners (not shown). The RE³⁺ cations (green) are located at the centre of a scalenohedron (not drawn out), where 8 of the 10 corners are occupied by the 48f O(1) and the 8b O(2) oxygen, the latter are shown in red.

Disordered oxygen vacancies (e.g. in oxygen deficient fluorites) favour higher oxygen ion mobility and conductivity.^13–16 Therefore, high oxygen mobility and conductivity in the pyrochlore structure was claimed to be favoured by a certain degree of A and B anti-site defects, because anti-site defects may be directly coupled to the oxygen vacancy disorder, i.e. increased anti-site defects directly induce increased oxygen vacancy disorder in the nominally oxygen ordered structure and improve oxygen ion conductivity.^13–15 In this context it should be noted that increasing concentrations of pyrochlore A and B anti-site defects can be regarded a precursor to the formation of the fluorite structure with a disordered arrangement of the cationic sub-lattice and the oxygen vacancies. On the other hand, some authors have reported that some degree of oxygen structural disorder can exists in pyrochlores despite a fully ordered cationic sub-lattice, as evidenced by Raman spectroscopy, and the anti-site and anion Frenkel defects may not always be directly coupled.^17,18

Here in this work the coupling of anti-site and Frenkel defects could not be confirmed for the HTO samples, because a negligible anti-site defect concentration was detected by synchrotron X-ray diffraction (SXRD), but Raman spectroscopy suggested considerable oxygen vacancy disorder in HTO. The latter finding was corroborated by significantly enhanced ionic oxygen vacancy conduction in the HTO sample as compared to GTO, detected by impedance spectroscopy on sintered ceramic pellets.

It has been established previously that the concentration of pyrochlore A and B anti-site defects depends on the details of the synthesis procedure.^17–19 Here in this work we demonstrate that the microwave (MW)-assisted method produces off-equilibrium (metastable) pyrochlore-type phases with varying amounts of anti-site defects, in agreement with other more recently developed alternative synthesis methods, e.g. mechanical milling.¹⁹ Traditionally, RE₂Ti₂O₇ compounds are prepared by solid state reactions, which require repeated and long synthesis procedures at temperatures of up to ≈1400 °C and intensive grinding at the initial and intermediate stages of processing to achieve single phase material.^20–22 In the last decades several alternative routes have been proposed such as microwave (MW) synthesis, molten salt mediated synthesis, co-precipitation of hydroxides, sol–gel and citrate based methods, and mechanical milling, where the time and temperature requirements for synthesis are significantly reduced.^19,23–26 However, these methods usually require a second calcination step in a conventional furnace to obtain phase pure materials and the total reaction time increases. MW-assisted synthesis may be particularly useful due to the nanometre-sized particles that can be obtained at reduced synthesis time and processing costs.^27–32 In the work presented here we use a domestic microwave oven for the first heat treatment process of only 20 min, followed by a 2 h calcination procedure at 1100 °C in a conventional furnace to obtain highly crystalline single phase materials.³³ We explore this fast MW-assisted synthetic route for RE₂Ti₂O₇ pyrochlores with RE = Gd, Ho. The nano-metric particle sizes may improve the sintering activity of the resulting powders, which is beneficial to obtain dense bulk materials by ceramic sintering to study the dielectric properties. Furthermore, a quick and economic sintering process may be relevant for potential industrial applications. By example, we present the microwave synthesis of Gd₂Ti₂O₇ (GTO) and Ho₂Ti₂O₇ (HTO) pyrochlores, and their structural, magnetic and dielectric properties.

2. Experimental

2.1. Synthesis

Highly reactive TiO₂ amorphous powder was previously obtained from titanium(IV) propoxide dissolved in isopropyl alcohol, and the mixture was hydrolysed by adding water. An amorphous bulky gel was obtained, which was filtered and dried at 80 °C for 12 hours. Furthermore, the respective RE-nitrates (RE(NO₃)₃·xH₂O) (99.9% Sigma-Aldrich) were used as precursor oxides, where the amounts of water of hydration (x = 4.61 for RE = Gd and x = 3.54 for RE = Ho) were determined previously by thermogravimetric analysis. For one sample batch ≈1.3 g of the stoichiometric precursor mixture was homogenized together with 5% (wt) carbon black powder, which serves as a microwave absorber to improve the heat transfer. The mixture was ground intimately and pressed into pellets of 13 mm diameter and ≈650 mg using a uniaxial press, and the pellets were placed into a small porcelain crucible inside another larger one stuffed with mullite. The crucibles were MW-irradiated in a domestic microwave oven operating at 2.45 GHz frequency and a power of 800 W. After MW irradiation for 20 min, in a second heating step the pellets were calcined at 1100 °C for 2 h using a conventional furnace. The 2 h holding time and 1100 °C temperature were determined by a trial-and-error procedure, where calcining at 800 °C for 12 h and at 1000 °C for 12 h both proved to be insufficient to obtain a single pyrochlore phase. Furthermore, a control experiment was performed to synthesize GTO powder at 1200 °C for 3 h without the previous microwave heating step, but again no single phase could be obtained. Additional control experiments were carried out to prove the reproducibility of the synthesis process by using different microwave furnaces under the same conditions. All together, we have used 3 different domestic microwave furnaces (Sanyo EM – S1057G ES2; Balay 3WMX1918X 17L; CATA FS 20 WH) all operating at 2.45 GHz frequency and 800 W. After the second calcination step the resulting phases were confirmed to be all reproducible by standard X-ray diffraction (XRD).

In the field of solid state synthesis especially domestic microwave furnaces are well-known to often entail problems with the reproducibility of the final products due to the lack of temperature control. In this work we did not encounter this problem, most likely due to the fact that we used a microwave heating source only for the first synthesis step to produce precursor powder followed by a second step calcination process in a conventional furnace. In the conventional furnace the temperature is well-controlled and reproducibility problems usually do not occur.

All samples were analysed by standard XRD and scanning electron microscopy (SEM) twice: first, after the initial microwave treatment and second, after the subsequent calcination treatment at 1100 °C in the conventional furnace. In each case the pellets were extracted from the microwave or the conventional furnaces and were ground into powder form. Three batches of the final single phase products were further heated at 1200 °C, 1300 °C and 1400 °C for 12 h each to study the temperature dependence of the concentration of anti-site defects. For ionic conductivity measurements by impedance spectroscopy, GTO and HTO pressed pellets of 5 mm diameter and 2 mm thickness were sintered at 1400 °C for 4 h (heating and cooling ramps of 2 °C min⁻¹). The relative densities of the sintered GTO and HTO pellets were ≈95% of the crystallographic value. Both faces of the pellets were covered with Au electrodes using dc sputtering to facilitate impedance spectroscopy measurements.

2.2. Characterization

The phase composition of all samples were determined by conventional X-ray diffraction (XRD) on a PANAnalytical X'Pert PRO MPD apparatus using CuK_α radiation.

High-resolution powder synchrotron X-ray diffraction (SXRD) patterns were collected at the SpLine beamline (BM25A) of the Spanish CRG at the European Synchrotron Radiation Facility (ESRF, Grenoble) with a fixed wavelength of λ = 0.49684897 Å (24954.112 eV). Powdered samples were placed inside capillaries with diameters ranging from 0.2–0.5 mm, where the capillaries were rotated during exposure. In each case the absorption was calculated to maximize the signal-to-time ratio for every sample. Data were collected in a continuous 2θ-scan mode from 3° to 35°.

Structural refinements using (S)XRD data were carried out by the Rietveld method using FULLPROF software.³⁴ A Pseudo-Voigt function was selected as the line profile and the corresponding parameters were refined. Furthermore, the set of pre-defined background points, scale factor, zero shift, lattice parameters, atomic O displacement and the overall Debye–Weller factors were refined. These overall factors were converted into individual isotropic Debye–Waller factors and refined. The cation occupation was also refined to detect possible anti-site defects.

Scanning electron microscopy (SEM) micrographs were collected on an FEI XL30® apparatus equipped with an attached analyser for energy dispersive spectroscopy (EDS).

Unpolarised Raman spectroscopy experiments were performed using a micro-Raman confocal spectrometer (Voyage™ BWS435-532SY, BW&Tek). An excitation wavelength of 532.0 nm was produced by a solid state laser with an incident power fixed at 10 mW. The spectrometer was equipped with an Olympus BX51 microscope allowing the collection of the Raman signal on backscattering configuration through a 50× long working distance objective. With this setup, the spectral resolution was about 4 cm⁻¹. A Chameleon™ CMLN-13S2C digital camera has also been coupled to the equipment.

Magnetic susceptibility measurements of GTO and HTO powder samples calcined at 1100 °C were performed in a Quantum Design XL-SQUID magnetometer in the temperature range of 2–300 K at 1 kOe applied magnetic field. The temperature dependence of the magnetic susceptibility was measured following zero-field-cooled and field-cooled (ZFC–FC) procedures with intermediate demagnetization at room temperature. Ferri-magnetic hysteresis cycles were recorded at 1.7 K from magnetization vs. applied field measurements.

Impedance spectroscopy was carried out on 1400 °C sintered ceramic pellets between 150 and 550 K using a Novocontrol Alpha-A High Performance Frequency Analyzer equipped with a nitrogen gas cooled sample chamber. A 100 mV amplitude alternating voltage signal was employed and the data was recorded between 0.5 Hz to 3 MHz in terms of the real and imaginary parts of the impedance (Z′–Z′′). The data were converted into the permittivity notation ε′–ε′′ using the standard conversion.³⁵ High temperature impedance spectroscopy was carried out using a Solartron 1260 Frequency Response Analyzer in the 1 Hz to 1 MHz range between 298 and 1273 K in different atmospheres (air, pure oxygen or pure Ar), using a 100 mV amplitude alternating voltage signal.

3. Results and discussion

3.1. Reaction pathways

Fig. 2 shows the conventional XRD patterns from the 20 min MW-irradiated precursor mixtures for the nominal GTO compound after the subsequent calcination at 800 °C (Fig. 2a). Calcining at 800 °C for 12 h proved to be suitable to remove the traces from the carbon black powder used as a microwave absorber, but the synthesis reaction was still not complete and a mixture of GTO and the unreacted precursors Gd₂O₃ and TiO₂ (anatase) is evident. The XRD pattern for the sample calcined at 1000 °C during 12 h (Fig. 2b) reveals that even at this elevated temperature some unreacted Gd₂O₃ and TiO₂ (rutile) still remain. A better result was obtained after calcining at 1100 °C for only 2 h (Fig. 3a) and a single pyrochlore phase with high crystallinity is evident. A similar behaviour is observed for the Ho-containing sample. Fig. 3a and b demonstrate that both GTO and HTO powders can be obtained as pure single phases by calcining the 20 min MW-treated powders at 1100 °C for 2 h. Thus, it seems that the key parameter is the temperature rather than the holding time to complete the synthesis reaction. On the contrary, the XRD pattern of a sample of GTO prepared by the conventional calcination treatment (without previous microwave irradiation) (Fig. 3c) reveals that the reaction is not complete in spite of using higher temperature and larger reaction times (1200 °C, 3 hours). This is not surprising since the preparation of pyrochlore oxides by traditional solid-state reaction from a mixture of oxides commonly requires repeated grinding and long heating cycles at temperatures higher than 1200 °C to achieve complete reaction.^20–22 Thus, we can confirm that the use of microwave heating is useful to reduce the reaction time, temperature and costs for the synthesis of RE-titanate pyrochlores.

Fig. 2 XRD pattern for Gd₂Ti₂O₇ powders irradiated by microwaves for 20 min and subsequently calcined at 800 °C (a) and 1000 °C (b) for 12 h. Besides the pyrochlore material (first row of vertical bars) unreacted Gd₂O₃ (second row) and TiO₂ (anatase in (a), rutile in (b), third row) are observed.

Fig. 3 XRD pattern for (a) Gd₂Ti₂O₇ and (b) Ho₂Ti₂O₇, obtained from MW-irradiated precursors calcined at 1100 °C for 2 h and (c) for a non-MW-irradiated Gd₂Ti₂O₇ sample calcined at 1200 °C for 3 h. In (a) and (b) only the pyrochlore phase is observed, in (c) pyrochlore (first row of vertical bars), unreacted Gd₂O₃ (second row) and TiO₂ (rutile, third row) are observed.

3.2. Microstructural characterization

Fig. 4 shows the backscattered-electron mode SEM micrographs of the single phase RE₂Ti₂O₇ final product powders after 20 min of microwave irradiation and 2 h calcination at 1100 °C. The powders are composed of agglomerations of submicron or nanometric spherical particles with high homogeneity and a sponge-like texture. This morphology may arise most likely from the large amount of gases produced during the decomposition of the starting nitrates and oxidation of active carbon to CO₂. It is worth mentioning that the small particle size persists after the second 1100 °C calcination step, facilitating a good sintering activity of the powders. Therefore, a short sintering process of the pressed pellets for 4 h at 1400 °C is sufficient to obtain highly densified ceramics as a result of significant and rapid particle growth, as demonstrated in Fig. 4c and d. EDS analyses confirmed the nominal metallic compositions (≈RE 50% and Ti 50%). Furthermore, the homogeneous contrast in the backscattered SEM images in Fig. 4 implies that RE and Ti cations are well dispersed across the samples discarding any segregation of impurity phases.

Fig. 4 SEM micrographs of the RE₂Ti₂O₇ samples. (a) and (b) correspond to Gd₂Ti₂O₇ and Ho₂Ti₂O₇ powder samples. (c) and (d) correspond to the respective pellets sintered at 1400 °C during 4 h.

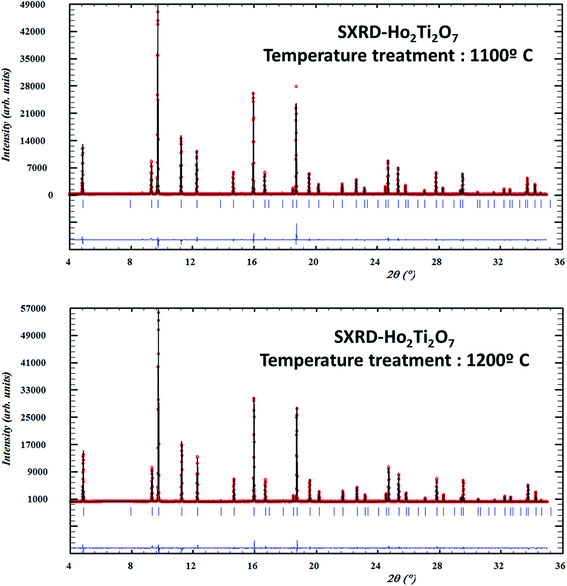
3.3. Analysis of anti-site defects by SXRD

As mentioned above (Section 1), the pyrochlore structure can be considered a superstructure of an anion-deficient fluorite atomic arrangement. Therefore, the pyrochlore diffraction pattern contains a set of strong peaks characteristic of the fluorite substructure plus an additional set of superstructure reflections. The intensities of the latter depend on factors like the degree of ordering, difference in the average scattering factors of the elements involved and distribution of oxygen vacancies.¹³ Superstructure peaks due to the pyrochlore long-range atomic ordering are evident in the SXRD patterns from the GTO and HTO samples treated at different temperatures from 1100 °C to 1400 °C (Fig. 5 and 6). Since the temperature for the pellet sintering process was 1400 °C, the structural results obtained from the 1400 °C heated samples may also be representative for the sintered pellets, which were analysed by impedance spectroscopy to determine the ionic conductivities (Section 3.6).

Fig. 5 Rietveld refinement of synchrotron XRD patterns of Ho₂Ti₂O₇ treated at 1100 °C and 1200 °C. Experimental pattern (red dotted line), calculated (black solid line), and their difference (blue bottom line) are depicted. Green vertical bars indicate the reflection positions.

Fig. 6 Rietveld refinement of synchrotron XRD patterns of Gd₂Ti₂O₇ treated at 1300 °C and 1400 °C. Experimental pattern (red dotted line), calculated (black solid line), and their difference (blue bottom line) are depicted. Green vertical bars indicate the reflection positions.

The structure factors (F_hkl) of the superstructure peaks depend on the difference of scattering power between the 16d and the 16c sites and the F_hkl factors for peaks with even h, k and l depend on the total of the scattering power in both positions. Therefore, the relative intensities of the superstructure peaks are a direct reflection of the cation distribution in the structure.

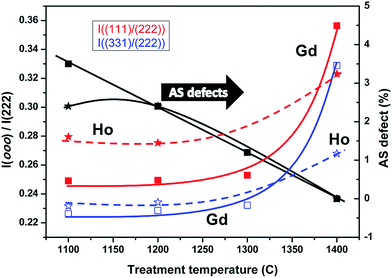
We started our structural refinements of the SXRD data with the fully ordered pyrochlore structure, where all RE ions are constrained to the 16d sites and the Ti to the 16c sites. However, it became evident from the fitting process that more scattering power should be located in the 16c site which could only be accomplished by allowing the exchange of RE and Ti cations from their nominal positions, i.e. the occurrence of A and B anti-site defects. The final refined cation distributions presented in Table 1 show a perceptible fraction of Gd and Ho cations to be located at the six-coordinated 16c site, which reduced after heating the powders at higher temperatures (up to 1400 °C). The anti-site defect percentages are 3.6% for Gd₂Ti₂O₇ and 2.4% for Ho₂Ti₂O₇ at 1100 °C. This is consistent with the different relative intensities of the superstructure peaks shown in Fig. 7, where the anti-site defect concentrations show clear temperature dependence. Generally, anti-site defects are more common when the A and B cations have similar ionic radii, whereas in the RE₂Ti₂O₇ case presented here the A- and B-site cationic radii are quite different and the anti-site defect concentration is then expected to be strongly temperature dependent.^18,19,36 The temperature dependence of the anti-site defect concentrations is summarized in Table 1.

Table 1 Structural parameters at room temperature for pyrochlore RE₂Ti₂O₇ (RE = Gd, Ho) obtained from synchrotron X-ray diffraction data on samples heated at different temperatures

	Ho2Ti2O7			Gd2Ti2O7
	1100 °C	1200 °C	1400 °C	1100 °C	1200 °C	1300 °C	1400 °C
a (Å)	10.10004(6)	10.09882(5)	10.09828(3)	10.18126(8)	10.18407(5)	10.18496(5)	10.18507(6)
A position	16d			16d
U × 100 (Å^2)	0.72(1)	0.74(2)	0.38(3)	0.84(1)	0.62(2)	0.56(3)	0.45(2)
Occ RE/Ti	1.952(3)/0.048(3)	1.952(2)/0.048(2)	2.000(2)/0.000(2)	1.929(3)/0.071(3)	1.952(2)/0.048(2)	1.976(2)/0.024(2)	2.000(2)/0.000(2)
B position	16c			16c
U × 100 (Å^2)	1.01(5)	1.03(3)	0.39(2)	1.22(2)	0.83(1)	0.65(2)	0.95(4)
Occ Ti/RE	1.952(3)/0.048(3)	1.952(2)/0.048(2)	2.000(2)/0.000(2)	1.929(3)/0.071(3)	1.952(2)/0.048(2)	1.976(2)/0.024(2)	2.000(2)/0.000(2)
O(1) position	48f			48f
X	0.4229(4)	0.4232(4)	0.4227(4)	0.4239(4)	0.4244(3)	0.4253(3)	0.42877(5)
U × 100 (Å^2)	0.71(2)	0.71(2)	0.42(1)	0.82(3)	1.13(1)	0.88(2)	0.93(1)
O(2) position	8b			8b
U × 100 (Å^2)	0.09(2)	0.02(4)	0.51(3)	0.09(2)	0.16(3)	0.01(2)	0.23(3)
χ^2	4.24	4.43	4.60	4.78	4.74	3.57	6.21
Rwp/Rexp (%/%)	9.63/4.67	9.13/4.34	9.36/4.36	10.7/4.92	9.23/4.24	7.59/4.02	12.3/3.94
RBragg	2.42	2.35	2.83	2.40	2.16	1.90	5.50
Space group	Fd3̄m (#227): 16d (1/2 1/2 1/2), 16c (0 0 0), 48f (x 1/8 1/8), 4b (3/8 3/8 3/8)			Fd3̄m (#227): 16d (1/2 1/2 1/2), 16c (0 0 0), 48f (x 1/8 1/8), 4b (3/8 3/8 3/8)

---

Fig. 7 Left axis: Temperature dependence of the intensity of the superstructure peaks (111) in red and (331) in blue, referred to that of the (222) peak for GTO (solid lines) and HTO (dashed lines). Right axis: Anti-site (AS)-defect concentrations for Gd₂Ti₂O₇ (solid squares) and Ho₂Ti₂O₇ (asterisks). Lines are a guide for the eyes.

The pyrochlore unit cell parameter is mainly determined by the size of the BO₆ distorted octahedra (=trigonal antiprisms) and, bearing in mind the ionic radii of RE³⁺ and Ti⁴⁺ cations, it is clear that a higher degree of occupation of the 16c sites by RE cations increases the size of the BO₆ units and concomitantly the unit cell.¹⁹ Since thermal treatment removes anti-site defects it would therefore be expected that heating at higher temperatures would result in smaller unit cell parameters. Additionally, the unit cell parameters may also be affected by a small concentration (δ) of non-stoichiometric oxygen vacancies (RE₂Ti₂O_7−δ), compensated by the formation of Ti³⁺.^37,38 By heating at high temperature in oxidizing conditions these anion vacancies would be filled, accompanied by oxidation of large Ti³⁺ cations to smaller Ti⁴⁺, and the unit cell parameter would again decrease. We believe that non-stoichiometric oxygen vacancies may well exist in our samples since we use strongly reducing carbon as MW-absorber and the obtained products would therefore be expected to be oxygen-deficient to a certain extent. Therefore, we presume that at least two mechanisms may operate at the same time during heat treatment at elevated temperatures in air: (i) cation re-distribution among A- and B-sites, and (ii) oxidation of Ti³⁺ to Ti⁴⁺ through incorporation of oxygen into non-stoichiometric anion vacancies. Both processes would induce shortening of the unit cell.

The unit cell size for HTO (Table 1) displays such a trend, whereas for GTO the unit cell shows an expansion as the temperature of the heat treatments increases. We suspect that the thermal expansion of the GTO lattice may dominate over the decreasing anti-site defect concentration and/or the concentration of non-stoichiometric oxygen vacancies may be significantly lower, which then results in a different evolution of the unit cell size. Alternatively, the GTO phase may be affected by additional structural variations.

3.4. Raman spectroscopy

Fig. 8 shows the Raman spectra for GTO and HTO samples heat treated at different temperatures. The observed Raman modes have been assigned to F_2g and A_1g modes according to the literature,^39–42 where some unassigned modes (small black arrows) have been interpreted as two-phonon modes. The Raman modes in Fig. 8 have different intensities due to the different RE³⁺ cations in GTO and HTO, which is expected according to the literature. The drastic change of Raman mode intensities with the heat treatment temperature observed in the GTO sample (but not in the HTO) is unusual and may point towards additional structural variations. This could possibly be correlated with the unusual changes of the unit cell volume mentioned above in Section 3.3.

Fig. 8 Raman shift. (a) Gd₂Ti₂O₇ (red) heat treated at 1100 °C, (b) Gd₂Ti₂O₇ heat treated at 1400 °C, (c) Ho₂Ti₂O₇ (blue) heat treated at 1200 °C, (d) Ho₂Ti₂O₇ heat treated at 1400 °C.

The main feature of the Raman spectra shown in Fig. 8 is the appearance of an additional phonon (large blue arrows) centred at 750 cm⁻¹ in HTO (but not in GTO). This mode has been observed previously in Y₂Zr_2−yTi_yO₇ pyrochlore structures and was associated with a substructure with varying oxygen coordination.⁴² We interpret the occurrence of this mode as a clear sign of oxygen disorder in the HTO, and the two types of defects, anti-site and Frenkel anion defects, may be uncoupled to a certain extent. This notion is corroborated by a strongly increased ionic oxygen vacancy conduction in the HTO sample as demonstrated below (Section 3.6) despite the absence of anti-site disorder detected by SXRD measurements (Section 3.3).

3.5. Magnetic properties of the magnetic structure

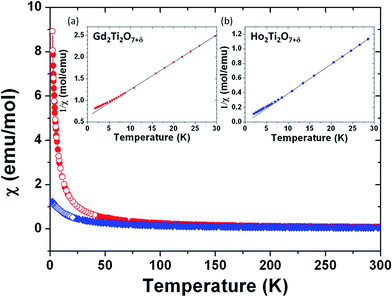
The magnetic structure of RE₂Ti₂O₇ (RE = Gd, Ho) pyrochlores is determined by the magnetically active RE-cations, which form a tetrahedral sublattice where the tetrahedral antiferromagnetic interactions exhibit strong frustration.⁴³ The magnetic ground state has been referred to as a spin ice, where a “two spins in, two spins out” configuration may be satisfied in every tetrahedron.^44,45

Fig. 9 shows the temperature dependence of the magnetic susceptibility for both powder samples. No significant differences between ZFC (solid marks) and FC (hollow marks) susceptibility curves are evident. The insets in Fig. 9 show plots of the reciprocal magnetic susceptibility 1/χ vs. T at low temperature, indicating a deviation from the Curie–Weiss law [χ = C/(T − θ)] below ≈10 K in both samples. The Curie–Weiss fits are indicated by black solid lines, which allowed the extraction of the Curie constant C, related to the effective magnetic moment μ_eff, and the Weiss constant θ. In the case of GTO a linear regression analysis yields μ_eff ≈ 5.7 μ_B/Gd³⁺ and θ ≈ −9.8 K. A negative θ value suggests that antiferromagnetic interactions may be predominant. For HTO, μ_eff ≈ 7.3 μ_B/Ho³⁺, and θ ≈ +0.2 K. The latter positive value suggests that ferromagnetic interactions may be predominant. The experimental magnetic moments are smaller than the theoretical ones: μ_eff = 7.9 μ_B for the free ion ⁸S_7/2 ground state of Gd³⁺ and 10.6 μ_B for the ⁵I₈ Ho³⁺ ground state. This discrepancy between theoretical and experimental magnetic moments may be related to the magnetic frustration commonly encountered in pyrochlore structures.

Fig. 9 Temperature dependence of the magnetic susceptibilities χ for Gd₂Ti₂O₇ (red circles) and Ho₂Ti₂O₇ (blue squares) at 1 kOe. Solid and empty symbols represent ZFC and FC data respectively. Insets: inverse susceptibility 1/χ. The black line represents the fit to the Curie–Weiss law. A deviation is demonstrated below ≈ 10 K.

Fig. 10 presents the magnetization vs. applied field plots at 1.7 K for GTO and HTO, where a small hysteresis is observed. In the case of HTO a magnetic saturation is observed, which confirms the positive value of the Weiss constant and the notion that a soft ferromagnetic component drives the magnetic behaviour. A more detailed investigation into the magnetic structure of the GTO and HTO phases in terms of neutron diffraction experiments may be indicated to elucidate the origin of the ferromagnetic component in HTO, but this goes behind the scope of the work presented here.

Fig. 10 Magnetic hysteresis loop at 1.7 K in the magnetic field range of −50 to 50 kOe for (a) Gd₂Ti₂O₇ (red circles) and (b) Ho₂Ti₂O₇ (blue squares). Insets: magnification of the hysteresis loops.

3.6. Dielectric properties

Impedance Spectroscopy (IS) data collected at 560 K for GTO and HTO ceramic pellets sintered at 1400 °C are shown in Fig. 11 in terms of the complex impedance plane plots of −Z′′ vs. Z′. For both samples (Fig. 11a and b) one regular semicircle is displayed. The data can therefore be modeled by a resistor–capacitor (RC) element where the resistance R corresponds to the respective semicircle diameter. The specific capacitance (discussed below) extracted from the single semicircles is in an order of magnitude that indicates that this dielectric contribution can be ascribed to an intrinsic grain interior bulk effect.⁴⁶

Fig. 11 Complex impedance plane plots of −Z′′ vs. Z′ for (a) Gd₂Ti₂O₇ (red open diamonds) and (b) Ho₂Ti₂O₇ (blue open diamonds) ceramic pellets. The equivalent circuits used for fitting the data are depicted in the figure insets. Solid black squares and lines indicate the fitted curves.

At the low frequency end the data points for the HTO sample in the −Z′′ vs. Z′ notation (Fig. 11b) align linearly in a “pike-like” fashion, which is inconsistent with the conventional RC element model. This behavior is commonly interpreted as a blocking effect of the electrode sample interface (IF).³⁵ This constitutes evidence for ionic charge transport where the blocking effect of the interface occurs as a result of the different types of dominating charge carriers in the Au electrodes (electrons) and in the ceramic (oxygen vacancies). Therefore, ionic oxygen vacancy conductivity in the HTO samples is indicated, and electronic contributions may be small. The charge transport across blocking electrode interfaces is usually by diffusion, which was not accounted for in the equivalent circuit model here, because rather complex circuit components such as Warburg elements are needed to describe diffusion processes by an equivalent circuit component.³⁵ For the GTO sample the interface pike contribution is not visible in Fig. 11a, most likely due to insufficient resolution at the low frequency end. The interface contribution may possibly appear at lower frequency. This may be attributed to the higher resistivity of the GTO sample, which indicates a slower charge transport mechanism at the same temperature, and the same features in the impedance spectra would be visible at lower frequency.

The resulting equivalent circuits used for fitting the data from GTO and HTO ceramic pellets are displayed in the insets of Fig. 11a and b and a good fit to the data can be obtained in the high and intermediate frequency range where the bulk contributions are dominant. It should be noted that the semicircles in Fig. 11 are slightly suppressed in a way that the semicircle center seems to be slightly shifted below the Z′ x-axis. This indicates a certain degree of non-ideality of the dielectric relaxation processes, which can be accounted for by connecting a constant phase element (CPE) in parallel to the ideal RC element.⁴⁷ The CPE behavior is usually explained in the framework of a broadening of the distribution of relaxation times τ across the macroscopic sample, where τ = RC, with R being the resistance and C the capacitance of an ideal RC element.^35,48

In both cases, for GTO and HTO, only one semicircle is evident from Fig. 11, although the pike-like interface contribution suggests ionic type charge transport, at least in the HTO. This is rather unusual, because ionic charge transport is understood to be inhibited by Schottky-type charge transport barriers at the grain boundary (GB) regions, and both bulk and GB contributions are expected to appear in form of two separated semicircles in −Z′′ vs. Z′ plots.⁴⁶ The reasons for the disappearance of the GB contributions are not entirely clear but the GB Schottky model may possibly not be valid here.

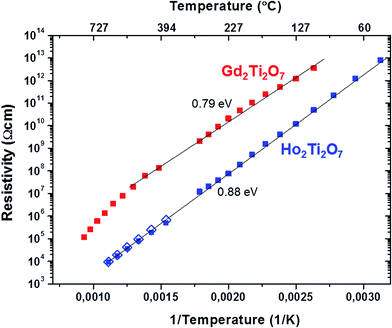
The ionic conductivity in the HTO sample is larger (the resistivity is lower) as compared to GTO, which is obvious from the different semicircle diameter (the difference is about a factor of 150). This large difference in resistivity is also evident in Fig. 12, where semi-logarithmic plots of resistivity ρ vs. reciprocal temperature 1/T are depicted. The resistivity values were obtained from the resistors in the equivalent circuits depicted in the insets of Fig. 11a and b. In the case of the HTO sample the open blue symbols represent resistivity values from impedance measurements under Ar atmosphere, which are almost identical to the ones from measurements under air (blue solid symbols). This implies that the ionic oxygen vacancy conduction in HTO may be independent from the ambient conditions.

Fig. 12 Resistivity vs. 1/T for the bulk contributions of Gd₂Ti₂O₇ (red squares) and Ho₂Ti₂O₇ (blue squares) ceramics obtained from the equivalent circuit fits. The respective charge transport activation energies were obtained from linear fits (black solid lines) to the Arrhenius plots (ln ρ vs. 1/T) and the respective values are given.

The curve for the GTO ceramic pellet (red solid symbols) shows a deviation from the linear behaviour above ≈500 °C (773 K), which may again be associated with the unusual changes in the GTO lattice parameter at high T (Section 3.3).

The activation energy E_A for the GTO ceramic was determined from the respective Arrhenius curves (ln ρ vs. 1/T, not shown here) in the linear regime below ≈500 K (773 °C) only, whereas the entire T-range was considered for HTO. E_A was found to be 0.79 eV and 0.88 eV for GTO and HTO respectively, which is in a typical range for oxygen ion conduction.^49–54 Both E_A values are rather similar, which suggests a similar charge transport mechanism. E_A was determined by assuming a linear Arrhenius behaviour of ρ = ρ₀ exp(E_A/k_BT). However, alternative models of ρ/T = ρ₀ exp(E_A/k_BT) have also been proposed in the literature,^55,56 in which case the activation energies would be slightly increased to 0.83 eV and 0.92 eV for GTO and HTO respectively. Within the second more advanced model the pre-exponential factors ρ₀ have been claimed to exhibit a reciprocal relationship with the concentration of mobile species. From our fits we find ρ₀ to be 1.3 10⁻¹ Ω cm K⁻¹ and 8.3 10⁻⁵ Ω cm K⁻¹ for GTO and HTO respectively. The concomitant increased concentration of mobile species in HTO is in agreement with the lower nominal resistivity, which may be interpreted in terms of increased oxygen vacancy conduction in agreement with the increased oxygen vacancy disorder in HTO detected by Raman spectroscopy (Section 3.4). Since our ionic conductivity measurements were performed on GTO and HTO pellets sintered at 1400 °C, A and B anti-site defects may well be excluded in both compositions (see Table 1) and the increased oxygen vacancy conduction in HTO may imply a certain decoupling of anti-site and anion Frenkel defects.

Fig. 13 shows the capacitance values obtained from the equivalent circuit fits, plotted as dielectric permittivity ε′ vs. temperature. The ε′ values obtained from the bulk semicircles in GTO and HTO are both in a range that is typical for bulk values.⁴⁶ The permittivity in the GTO is perceptibly increased as compared to the HTO, despite the equivalent crystal structure and similar cationic composition. The reasons for this increase are unclear, but we suspect that it may be correlated with the anomalous increase of the GTO unit cell (Section 3.3) and the significant changes in the Raman mode intensities (Section 3.4), both with increasing the heat treatment temperature. Although the HTO phase may be more relevant for applications due to an increased ionic conductivity, the GTO sample exhibits interesting unit cell volume changes accompanied by unusual Raman mode intensities, and both GTO and HTO species may deserve further research work in the future.

Fig. 13 Dielectric permittivity vs. temperature data using the capacitance values for the bulk contributions of Gd₂Ti₂O₇ (red squares) and Ho₂Ti₂O₇ (blue squares) ceramics obtained from the equivalent circuit fits. The temperature independent intrinsic bulk dielectric permittivity is indicated by the black lines and the respective values are given.

Both, the resistivity ρ and dielectric permittivity ε′ values presented in Fig. 12 and 13 were reproducible in control samples of GTO and HTO composition within an experimental error of ≈10%, which may arise from the uncertainty in measuring the pellet dimensions to calculate the specific parameters ρ and ε′.

4. Conclusions

We have successfully synthesized the two representatives RE = Gd, Ho from the RE₂Ti₂O₇ pyrochlore family using a microwave assisted synthesis route. The GTO and HTO phases obtained show small particle sizes with a high sintering activity. RE–Ti cationic anti-site defects were found to decrease in concentration with increasing temperature starting from 1100 °C, and completely disappear at 1400 °C. GTO shows a predominantly antiferromagnetic structure, whereas HTO exhibits magnetic saturation and a ferromagnetic component. Impedance spectroscopy data revealed enhanced ionic oxygen vacancy conduction in the HTO sample, which may be associated with oxygen vacancy disorder revealed by Raman spectroscopy that is uncoupled from the anti-site defects.

Acknowledgements

We thank the Spanish Ministerio de Ciencia e Innovación and the Comunidad de Madrid for funding the projects MAT2013-64452-C4-1-R and S2013MIT-2753 respectively. Financial support from Universidad CEU San Pablo is acknowledged. We thank the Spanish Ministerio de Ciencia e Innovación (MICINN) and Consejo Superior de Investigaciones Científicas (CSIC) for financial support and for provision of synchrotron radiation facilities. We would like to thank the beamline staff (German Castro y Alvaro Muñoz) for assistance in using beamline BM25-SpLine. R. S. wishes to acknowledge a Ramon y Cajal fellowship from the MICINN/MINECO in Spain. Thanks to Jacobo Santamaría, Carlos León and Alberto Rivera-Calzada for allowing use and help with the Novocontrol impedance spectroscopy facilities at the GFMC.

References

1. J. E. Greedan, in Functional Oxides, ed. D. W. Bruce, D. O'Hare and R. I. Walton, Wiley, 2011, ch. 2, pp. 41–117.
2. M. Mirsaneh, B. E. Hayden, E. Furman, S. Perini, M. T. Lanagan and I. M. Reaney, Appl. Phys. Lett., 2012, 100, 082901.
3. P. Holtappels, F. W. Poulsen and M. Mogensen, Solid State Ionics, 2000, 135, 675–679.
4. M. A. Subramanian, G. Aravamudan and G. V. Subba Rao, Prog. Solid State Chem., 1983, 15, 55–143.
5. D. J. P. Morris, D. A. Tennant, S. A. Grigera, B. Klemke, C. Castelnovo, R. Moessner, C. Czternasty, M. Meissner, K. C. Rule, J.-U. Hoffmann, K. Kiefer, S. Gerischer, D. Slobinsky and R. S. Perry, Science, 2009, 326, 411–414.
6. X. W. Dong, K. F. Wang, S. J. Luo, J. G. Wan and J. M. Liu, J. Appl. Phys., 2009, 106, 4.
7. Z. Hiroi and M. Hanawa, J. Phys. Chem. Solids, 2002, 63, 1021–1026.
8. S. X. Wang, L. M. Wang, R. C. Ewing and K. V. Govindan Kutty, Nucl. Instrum. Methods Phys. Res., Sect. B, 2000, 169, 135–140.
9. D. P. Reid, M. C. Stennett and N. C. Hyatt, J. Solid State Chem., 2012, 191, 2–9.
10. C. R. Stanek, L. Minervini and R. W. Grimes, J. Am. Ceram. Soc., 2002, 85, 2792–2798.
11. R. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767.
12. P. Nachimuthu, S. Thevuthasan, M. H. Engelhard, W. J. Weber, D. K. Shuh, N. M. Hamdan, B. S. Mun, E. M. Adams, D. E. McCready, V. Shutthanandan, D. W. Lindle, G. Balakrishnan, D. M. Paul, E. M. Gullikson, R. C. C. Perera, J. Lian, L. M. Wang and R. C. Ewing, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 100101.
13. B. J. Wuensch, K. W. Eberman, C. Heremans, E. M. Ku, P. Onnerud, E. M. E. Yeo, S. M. Haile, J. K. Stalick and J. D. Jorgensen, Solid State Ionics, 2000, 129, 111.
14. J. Chen, J. Lian, L. M. Wang, R. C. Ewing, R. G. Wang and W. Pan, Phys. Rev. Lett., 2002, 88, 105901.
15. P. K. Moon and H. L. Tuller, MRS Symposia Proceedings No. 135: Solid State Ionics, Pittsburgh, 1989, p. 149.
16. A. Rivera-Calzada, M. R. Diaz-Guillen, O. J. Dura, G. Sanchez-Santolino, T. J. Pennycook, R. Schmidt, F. Y. Bruno, J. Garcia-Barriocanal, Z. Sefrioui, N. M. Nemes, M. Garcia-Hernandez, M. Varela, C. Leon, S. T. Pantelides, S. J. Pennycook and J. Santamaria, Adv. Mater., 2011, 23, 5268–5274.
17. K. J. Moreno, A. F. Fuentes, U. Amador, J. Santamarıa and C. Leon, J. Non-Cryst. Solids, 2007, 353, 3947–3955.
18. K. J. Moreno, A. F. Fuentes, M. Maczka, J. Hanuza, U. Amador, J. Santamaría and C. León, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 184303.
19. A. F. Fuentes, K. Boulahya, M. Maczka, J. Hanuza and U. Amador, Solid State Sci., 2005, 7, 343–353.
20. A. Garbout, I. Ben Taazayet-Belgacem and M. Férid, J. Alloys Compd., 2013, 573, 43–52.
21. M. Roy, I. Bala and S. K. Barbar, J. Therm. Anal. Calorim., 2012, 110, 559–565.
22. R. S. Pavlov, J. B. C. Castelló, V. B. Marzá and J. M. Hohembergerger, J. Am. Ceram. Soc., 2002, 85, 1197–1202.
23. A. V. Shlyakhtina, O. K. Karyagina and L. G. Shcherbakova, Inorg. Mater., 2004, 40, 59–65.
24. L. Zhang, H. Zhong, W. Zhang, L. Lu, X. Yang and X. Wang, J. Alloys Compd., 2008, 463, 466–470.
25. M. L. Hand, M. C. Stennett and N. C. Hyatt, J. Eur. Ceram. Soc., 2012, 32, 3211–3219.
26. X. Lu, Y. Ding, H. Dan, S. Yuan, X. Mao, L. Fan and Y. Wu, Ceram. Int., 2014, 40, 13191–13194.
27. J. Zhao and W. Yan, in Modern Inorganic Synthetic Chemistry, Elsevier, Amsterdam, 2011, pp. 173–195,  DOI:10.1016/b978-0-444-53599-3.10008-3.
28. M. Gupta and E. W. W. Leong, Microwaves and Metals, Wiley, 2008.
29. J. Prado-Gonjal, A. M. Arévalo-López and E. Morán, Mater. Res. Bull., 2011, 46, 222–230.
30. J. Prado-Gonjal, R. Schmidt, J.-J. Romero, D. Ávila, U. Amador and E. Morán, Inorg. Chem., 2013, 52, 313–320.
31. J. Prado-Gonjal, R. Schmidt and E. Morán, Inorganics, 2015, 3, 101.
32. R. Schmidt, J. Prado-Gonjal and E. Morán, in CRC Concise Encyclopedia of Nanotechnology, ed. B. Kharisov, O. Kharissova and U. Ortiz-Mendez, CRC Press Taylor & Francis Group, Boca Raton (USA), 2015, ch. 46.
33. J. Prado-Gonjal, R. Schmidt and E. Morán, in Perovskite: Crystallography, Chemistry and Catalytic Performance, ed. J. Zhang and H. Li, Nova Science Pub Incorporated, 2012, pp. 117–140.
34. J. Rodriguez-Carvajal, Satellite Meeting on Powder diffraction of the XV Congress of the IUCr, 1990.
35. E. Barsukov and J. Macdonald, Impedance Spectroscopy: Theory, Experiment and Applications, John Wiley & Sons Inc., Hoboken, 2005.
36. P. K. Moon and H. L. Tuller, MRS Online Proc. Libr., 1988, 135, 149,  DOI:10.1557/proc-135-149.
37. D. V. West, T. M. McQueen, Q. Huang and R. J. Cava, J. Solid State Chem., 2008, 181, 1753–1758.
38. G. Sala, M. J. Gutmann, D. Prabhakaran, D. Pomaranski, C. Mitchelitis, J. B. Kycia, D. G. Porter, C. Castelnovo and J. P. Goff, Nat. Mater., 2014, 13, 488–493.
39. M. T. Vandenborre, E. Husson, J. P. Chatry and D. Michel, J. Raman Spectrosc., 1983, 14, 63–71.
40. F. W. Poulsen, M. Glerup and P. Holtappels, Solid State Ionics, 2000, 135, 595–602.
41. B. P. Mandal, A. Banerji, V. Sathe, S. K. Deb and A. K. Tyagi, J. Solid State Chem., 2007, 180, 2643–2648.
42. M. Glerup, O. F. Nielsen and F. W. Poulsen, J. Solid State Chem., 2001, 160, 25–32.
43. K. Matsuhira, Y. Hinatsu, K. Tenya and T. Sakakibara, J. Phys.: Condens. Matter, 2000, 12, L649.
44. T. Fennell, P. P. Deen, A. R. Wildes, K. Schmalzl, D. Prabhakaran, A. T. Boothroyd, R. J. Aldus, D. F. McMorrow and S. T. Bramwell, Science, 2009, 326, 415–417.
45. A. P. Sazonov, A. Gukasov and I. Mirebeau, J. Phys.: Condens. Matter, 2011, 23, 164221.
46. J. T. S. Irvine, D. C. Sinclair and A. R. West, Adv. Mater., 1990, 2, 132.
47. E. J. Abram, D. C. Sinclair and A. R. West, J. Electroceram., 2003, 10, 165.
48. R. Schmidt, W. Eerenstein, T. Winiecki, F. D. Morrison and P. A. Midgley, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 245111.
49. J. Prado-Gonjal, R. Schmidt, J. Espíndola-Canuto, P. Ramos-Alvarez and E. Morán, J. Power Sources, 2012, 209, 163–171.
50. M. A. Frechero, O. J. Durá, M. R. Díaz-Guillén, K. J. Moreno, J. A. Díaz-Guillén, J. García-Barriocanal, A. Rivera-Calzada, A. F. Fuentes and C. León, J. Non-Cryst. Solids, 2015, 407, 349–354.
51. L. G. Shcherbakova, J. C. C. Abrantes, D. A. Belov, E. A. Nesterova, O. K. Karyagina and A. V. Shlyakhtina, Solid State Ionics, 2014, 261, 131–140.
52. J. Prado-Gonjal, R. Heuguet, D. Muñoz-Gil, A. Rivera-Calzada, S. Marinel, E. Morán and R. Schmidt, Int. J. Hydrogen Energy, 2015 DOI:10.1016/j.ijhydene.2015.07.161.
53. M. R. Díaz-Guillén, M. A. Frechero, J. A. Díaz-Guillén, A. F. Fuentes and C. León, J. Electroceram., 2015, 34, 15–19.
54. M. Stojmenović, M. Žunić, J. Gulicovski, D. Bajuk-Bogdanović, I. Holclajtner-Antunović, V. Dodevski and S. Mentus, J. Mater. Sci., 2015, 50, 3781–3794.
55. B. P. Mandal, S. K. Deshpande and A. K. Tyagi, J. Mater. Res., 2008, 23, 911–916.
56. K. J. Moreno, G. Mendoza-Suárez, A. F. Fuentes, J. García-Barriocanal, C. León and J. Santamaria, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 132301.

---