Influence of the alloying elements Re, Co and W on the propagation of the Ni/Ni3Al interface crack
Shu-Lan Liua,
Chong-Yu Wang*ab and
Tao Yua
aCentral Iron and Steel Research Institute, Beijing 100081, PR China. E-mail: cywang@mail.tsinghua.edu.cn
bDepartment of Physics, Tsinghua University, Beijing 100084, PR China
First published on 9th June 2015
Abstract
The influence of the alloying elements Re, Co and W on the propagation of the (010)[101] Ni/Ni3Al interface crack has been investigated by molecular dynamics simulations and the discrete-variational method. The simulation results show that the interface crack propagates in a brittle manner at low temperature (5 K), but in a ductile manner at high temperature (1273 K), both with and without the addition of alloying elements. Owing to the scientific and technological importance of superalloys, the effects of the chemical bonding behavior between the alloying element X (X = Re, Co, or W) and Ni atoms on the crack shape, crack propagation velocity, and dislocation emission were investigated. At low temperature, the alloying elements Re and W inhibit the propagation of the Ni/Ni3Al interface crack, while at high temperature Re, Co and W can improve the ductility of Ni-based single-crystal superalloys. Furthermore, the adhesion work of the interface, surface energy, and unstable stacking energy were calculated to understand the propagation mechanism of the Ni/Ni3Al interface crack because of alloying element addition. The results of this study may provide useful information for the design of Ni-based superalloys.
1. Introduction
Because of their outstanding high-temperature mechanical properties, Ni-based single-crystal (SC) superalloys are important high-temperature materials, and they are used in turbine blades of advanced aircraft engines.1,2 The typical microstructure of these alloys is composed of the ordered L12 γ′-Ni3Al phase coherently embedded in a solid solution matrix of the γ-Ni phase. Because of the chemical composition and structural character, Ni-based SC superalloys are much stronger than pure γ or γ′ single-phase materials at high temperature.3–5 The properties of the γ/γ′ interface have a great influence on the performance of Ni-based superalloys. Thus, it is important to study the γ-Ni/γ′-Ni3Al interface.The strength of the γ/γ′ interface can be significantly improved by the addition of alloying elements, such as Re, Ta, W, Mo, Ru, and Co. In the past few years, the Ni/Ni3Al interface has been investigated using density functional theory. Chen et al.6 investigated the strengthening effect of alloying elements on the Ni/Ni3Al interface by calculating the bond orders, and showed that the rupture strength of Ni-based SC superalloys can be improved by Re, Ta, W, and Mo. Other studies7–11 have found that the binding strength, ductility, rupture strength, and toughness of the γ/γ′ interface can be improved by the addition of the refractory elements Re and Ru. Moreover, it has been reported that Co has little effect on improving the strength of the γ/γ′ interface.8 Recently, Liu et al.12 investigated the influence of Re on the propagation of the Ni/Ni3Al interface crack by the molecular dynamics (MD) method, and they found that Re is able to inhibit the crack propagation at low temperature and improve the ductility of superalloys because of the strong bond strength of Ni–Re.
In general, the final fracture of materials is caused by the breaking of atomic bonds, and the rupture strength can be improved by forming stronger atomic bonds during crack propagation. Improvement of the atomic bonds can be achieved by certain alloying elements. At present, in view of the construction of Ni–Al–X (X = Re, Co, or W) embedded-atom method (EAM) potentials13–15 and the important influence of Re, Co, and W on the mechanical properties of superalloys,16–19 it is essential to investigate the influence of these three alloying elements on the propagation of the Ni/Ni3Al interface crack at the atomic scale.
In the present study, 1 or 2 at% X (X = Re, Co, or W) atoms were randomly doped in the Ni matrix of the Ni/Ni3Al interface system to investigate the influence of alloying element X on the propagation of the Ni/Ni3Al interface crack at low (5 K) and high (1273 K) temperatures. Here, we investigate the crack propagation velocity, crack tip shape, and dislocation emission. The surface energy, unstable stacking energy, adhesion work of the interface, and bonding strength between atoms were also calculated to analyze the reasons for the influences of the alloying elements.
2. Model and simulation conditions
In the present study, the simulation model is divided into two parts by the (010) plane. The upper part is Ni3Al and the lower part is Ni, and the lattice constants for both parts are kept the same for the assumption of coherence. A sharp crack in the Ni/Ni3Al interface is obtained according to the anisotropic elastic displacement field.20 As shown in Fig. 1, the crack surface is the (010) plane, and the crack front is oriented along the [101] direction. The crack model consists of 200 atomic layers along the x[10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] direction, 160 atomic layers along the y[010] direction, and 60 atomic layers along the z[101] direction, including 480
] direction, 160 atomic layers along the y[010] direction, and 60 atomic layers along the z[101] direction, including 480![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms. Two larger simulation boxes (one with 200 atomic layers along the x and y directions, respectively, and 60 atomic layers along the z direction; and another with 200 atomic layers along the x direction, 160 atomic layers along the y direction, and 80 atomic layers along the z direction) were tested. It was found that the simulation results, such as the configuration evolution, elastic constants, surface energy, and crack propagation velocity, were insensitive to the system size. Thus, the smaller system size was used for the simulations. The initial crack length was about l = 50 Å. In Ni-based SC superalloys, it is known that the alloying elements Re and Co tend to distribute in the γ phase, while W uniformly distributes in both the γ and γ′ phases.21,22 In the present study, it was confirmed that the crack propagates in the γ-Ni matrix phase near the interface (as shown in Sections 3.2.1 and 3.3.1), and the path of the crack propagation did not change even the X atoms were randomly distributed in the Ni3Al phase of the Ni/Ni3Al superalloy system. Thus, 1 or 2 at% X (X = Re, Co, or W) atoms were randomly doped into the Ni matrix of the Ni/Ni3Al interface model to compare the effects of the three alloying elements.
000 atoms. Two larger simulation boxes (one with 200 atomic layers along the x and y directions, respectively, and 60 atomic layers along the z direction; and another with 200 atomic layers along the x direction, 160 atomic layers along the y direction, and 80 atomic layers along the z direction) were tested. It was found that the simulation results, such as the configuration evolution, elastic constants, surface energy, and crack propagation velocity, were insensitive to the system size. Thus, the smaller system size was used for the simulations. The initial crack length was about l = 50 Å. In Ni-based SC superalloys, it is known that the alloying elements Re and Co tend to distribute in the γ phase, while W uniformly distributes in both the γ and γ′ phases.21,22 In the present study, it was confirmed that the crack propagates in the γ-Ni matrix phase near the interface (as shown in Sections 3.2.1 and 3.3.1), and the path of the crack propagation did not change even the X atoms were randomly distributed in the Ni3Al phase of the Ni/Ni3Al superalloy system. Thus, 1 or 2 at% X (X = Re, Co, or W) atoms were randomly doped into the Ni matrix of the Ni/Ni3Al interface model to compare the effects of the three alloying elements.
 | ||
| Fig. 1 Structural model of the Ni/Ni3Al interface crack. The blue line is the interface and the red lines are the upper and lower crack surfaces. | ||
In experiments, the γ/γ′ (Ni/Ni3Al) interface of Ni-based SC superalloys is a diffuse interface with a width of about 1–3 nm.22,23 There are two interfacial widths, one corresponding to an order–disorder transition and the other to compositional transition across the interface.23 In this work, our purpose is focused on the doping effect of alloying elements on the Ni/Ni3Al interface. Thus, the Ni/Ni3Al interface model without transition layers was adopted in the present study.
As shown in Fig. 2, three different types of mode I interface cracks were originally constructed as follows. (i) The upper crack surface consists of Ni atoms, and the lower crack surface consists of Ni and Al atoms (Fig. 2(a)). (ii) The upper crack surface consists of Ni and Al atoms, and the lower crack surface consists of Ni atoms (Fig. 2(b)). (iii) Both of the crack surfaces consist of Ni atoms (Fig. 2(c)). In the present study, the MD simulations showed that the crack always propagates along the Ni–Ni layers near the Ni/Ni3Al interface, as shown in Fig. 2(c), which is consistent with experiments.24–26 Therefore, the type (iii) interface crack model was used to perform the following simulations. Fig. 3 shows the atomic configuration of the Ni/Ni3Al interface systems used in this study with 2 at% X (X = Re, Co, or W) atoms at the crack tip before relaxation.
The crack system was loaded in mode I, and strain loading was performed in the y[010] direction. The strain rate was ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 1 × 109 s−1. The periodic boundary condition was applied in the direction parallel to the crack front, and fixed boundary conditions (the outermost four atomic layers were fixed) were used in the x[10
= 1 × 109 s−1. The periodic boundary condition was applied in the direction parallel to the crack front, and fixed boundary conditions (the outermost four atomic layers were fixed) were used in the x[10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] and y[010] directions. In the MD simulations, Newton's equations of motion were solved with the Gear algorithm.27 The time steps were 5 × 10−15 and 1 × 10−15 s at 5 and 1273 K, respectively. In the simulation process, the temperature was kept constant with the velocity renormalization technique. The Ni–Al–X (X = Re, Co, or W) embedded-atom method (EAM) potentials13–15 and the XMD program28 were used.
] and y[010] directions. In the MD simulations, Newton's equations of motion were solved with the Gear algorithm.27 The time steps were 5 × 10−15 and 1 × 10−15 s at 5 and 1273 K, respectively. In the simulation process, the temperature was kept constant with the velocity renormalization technique. The Ni–Al–X (X = Re, Co, or W) embedded-atom method (EAM) potentials13–15 and the XMD program28 were used.
3. Results and discussion
3.1 Mechanical parameters of the Ni matrixes with and without X (X = Re, Co, or W) addition
To examine the reliability of the Ni–Al–X (X = Re, Co, or W) EAM potentials, we calculated the three independent elastic constants C11, C12, and C44, the bulk modulus B, the shear modulus G, Young's modulus E, and the lattice constant a for the prefect Ni matrixes with 0, 1, and 2 at% X atoms.The simulated results are listed in Table 1. Herein, the bulk modulus B = (C11 + 2C12)/3 and the shear modulus G were calculated as the arithmetic Hill average:,29 G = (GV + GR)/2, where GV = (C11 − C12 + 3C44)/5 and GR = 5/(4S11 − 4S12 + 3S44) (S11, S12, and S44 are the elastic compliances30) are the Voigt and Reuss bounds, respectively. Young's modulus E was obtained as E = 9GB/(G + 3B). In Table 1, the lattice constant of pure Ni is 3.52 Å, which is in agreement with previous theoretical and experimental results.31,32 With the addition of Re or W atoms, the lattice constant of the system increases, while it dose not change with the addition of Co atoms. This can be explained by the different atomic radii of the host and alloying atoms. The radii of Re (1.37 Å) and W (1.37 Å) are larger than that of the host atom Ni (1.25 Å), and the radius of Co (1.25 Å) is comparable with that of the host atom. Furthermore, except for Co, the values of C11, C12, C44, B, E, and G increase with the addition of Re or W atoms. The higher the concentration of Re or W atoms, the larger the values of Cij, B, E, and G, which reveals that Re and W can improve the mechanical strength of superalloys. These results are consistent with previous studies.33,34 The ductile/brittle behavior of the material is related to the ratio of G/B or Poisson's ratio ν (ν = (3B − 2G)/2(3B + 2G)). The lower the value of G/B or the higher the value of ν, the more ductile the material. From Table 1, with increasing concentration of Re or W, the ratio of G/B decreases and the value of ν increases. However, the addition of Co has no effect on the values of G/B and ν. This means that Re and W can increase the ductility of superalloys at high temperature. It is clear from Table 1 that different elements have different effects on the elastic properties of the Ni matrix.
| System | C11 (GPa) | C12 (GPa) | C44 (GPa) | B (GPa) | G (GPa) | E (GPa) | G/B | ν | a (Å) | |
|---|---|---|---|---|---|---|---|---|---|---|
| a Ref. 31.b Ref. 32. | ||||||||||
| Ni | This work | 237 | 150 | 127 | 179.0 | 82.7 | 215.4 | 0.462 | 0.299 | 3.520 |
| EAMa | 241 | 151 | 127 | 181.0 | 83.8 | 217.9 | 0.463 | 0.299 | 3.52 | |
| Expb | 246 | 147 | 125 | 180.0 | 86.2 | 223.0 | 0.478 | 0.293 | 3.52 | |
| Ni(Re) | 1 at% Re | 239 | 152 | 128 | 181.0 | 83.1 | 216.2 | 0.459 | 0.301 | 3.524 |
| 2 at% Re | 241 | 154 | 129 | 183.0 | 83.5 | 217.5 | 0.456 | 0.302 | 3.527 | |
| Ni(Co) | 1 at% Co | 236 | 149 | 126 | 178.0 | 82.3 | 213.9 | 0.462 | 0.299 | 3.519 |
| 2 at% Co | 234 | 148 | 125 | 176.7 | 81.6 | 212.0 | 0.462 | 0.299 | 3.519 | |
| Ni(W) | 1 at% W | 238 | 152 | 128 | 180.7 | 82.7 | 215.3 | 0.458 | 0.301 | 3.524 |
| 2 at% W | 239 | 154 | 129 | 182.3 | 82.8 | 215.6 | 0.454 | 0.303 | 3.528 | |
In addition, for pure Ni, the difference of the elastic constants between the present study and previous theoretical and experimental results31,32 is negligible. Thus, it can be concluded that the Ni–Al–X (X = Re, Co, or W) EAM potentials well describe the systems in the present study.
3.2 Influence of alloying element on crack propagation at low temperature
To investigate the influence of alloying element X (X = Re, Co, or W) on brittle crack propagation of the Ni/Ni3Al interface at low temperature, the structure evolution of the crack tip and the crack propagation velocity at 5 K were simulated. In addition, the adhesion work (Wad) of the interface was calculated to investigate the reason for the influence of the alloying elements on the crack propagation velocity at low temperature.![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 1 × 109 s−1 with 2 at% X (X = Re, Co, or W). From the evolution configurations of the crack tip in Fig. 4, it can be seen that the interface crack propagates in a cleavage manner and the crack tip retains the original sharp shape (as shown in Fig. 2) at low temperature with and without the alloying element addition. During the process of crack propagation, there is no dislocation near the crack tip even with the addition of alloying atoms. Moreover, the crack path does not change and the crack propagates along the Ni/Ni3Al interface, which is in agreement with experimental studies.24–26
= 1 × 109 s−1 with 2 at% X (X = Re, Co, or W). From the evolution configurations of the crack tip in Fig. 4, it can be seen that the interface crack propagates in a cleavage manner and the crack tip retains the original sharp shape (as shown in Fig. 2) at low temperature with and without the alloying element addition. During the process of crack propagation, there is no dislocation near the crack tip even with the addition of alloying atoms. Moreover, the crack path does not change and the crack propagates along the Ni/Ni3Al interface, which is in agreement with experimental studies.24–26
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 1 × 109 s−1 at 5 K with and without the addition of alloying element X (X = Re, Co, or W). From Table 2, the crack propagation velocity clearly decreases with the addition of 2 at% Re or W atoms, but not with the addition of Co. For example, with the addition of 2 at% Re and W, the crack propagation velocities were 274.3 and 229.7 m s−1 at 30 ps, which are 8.8% and 23.7% less than the crack propagation velocity without alloying element addition (300.9 m s−1), respectively. In contrast, the crack propagation velocity increases by 4.2% with 2 at% Co addition. The order of the crack propagate velocity with the alloying element addition is Co > No > Re > W (“No” means “the interface system without the addition of alloying element”). This indicates that Re and W can reduce the brittle crack propagation velocity of the Ni/Ni3Al interface at low temperature, and W has the greatest effect. This may be related to the bonding strength between atoms, which will be discussed in Section 3.4.
= 1 × 109 s−1 at 5 K with and without the addition of alloying element X (X = Re, Co, or W). From Table 2, the crack propagation velocity clearly decreases with the addition of 2 at% Re or W atoms, but not with the addition of Co. For example, with the addition of 2 at% Re and W, the crack propagation velocities were 274.3 and 229.7 m s−1 at 30 ps, which are 8.8% and 23.7% less than the crack propagation velocity without alloying element addition (300.9 m s−1), respectively. In contrast, the crack propagation velocity increases by 4.2% with 2 at% Co addition. The order of the crack propagate velocity with the alloying element addition is Co > No > Re > W (“No” means “the interface system without the addition of alloying element”). This indicates that Re and W can reduce the brittle crack propagation velocity of the Ni/Ni3Al interface at low temperature, and W has the greatest effect. This may be related to the bonding strength between atoms, which will be discussed in Section 3.4.
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 1 × 109 s−1 at 5 K. Ni (2 at% X) means 2 at% X randomly doped in the Ni matrix
= 1 × 109 s−1 at 5 K. Ni (2 at% X) means 2 at% X randomly doped in the Ni matrix
| Ni/Ni3Al | Ni (2 at% Re)/Ni3Al | Ni (2 at% Co)/Ni3Al | Ni (2 at% W)/Ni3Al | |
|---|---|---|---|---|
| Vcrack (at 30 ps) | 300.9 | 274.3 | 313.5 | 229.7 |
| Vcrack (at 35 ps) | 334.2 | 311.7 | 347.7 | 267.6 |
| Vcrack (at 40 ps) | 401.1 | 374.1 | 411.3 | 336.3 |
As shown in Fig. 5, the simulation model contained 8000 atoms, and had dimensions of 50.4 × 71.3 × 25.2 Å3 in the x[10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ], y[010], and z[101] directions, respectively. Periodic boundary conditions were used in the x and z directions, and the free boundary condition was used in the y direction. The Wad of the interface can be obtained by the following expression:5,12,36
], y[010], and z[101] directions, respectively. Periodic boundary conditions were used in the x and z directions, and the free boundary condition was used in the y direction. The Wad of the interface can be obtained by the following expression:5,12,36
| Wad = (ENi + ENi3Al − ENi/Ni3Al)/S | (1) |
Table 3 lists the Wad values of the systems with and without the addition of alloying element X (X = Re, Co, or W) in interface layers i and j (as shown in Fig. 5). From Table 3, the addition of Re or W atoms can effectively increase the adhesion work of the Ni/Ni3Al interface. For example, compared with the Ni/Ni3Al interface system without alloying element addition, the values of Wad increase by 1.43% and 2.69% with the addition of 2 at% Re and W atoms, respectively, but Wad decreases by 0.23% with 2 at% Co addition. The magnitude of the change of the Wad value with alloying elements is in the order: W > Re > Co, which is the opposite trend to the influence of the alloying elements on the interface brittle crack propagation velocity (as discussed in Section 3.2.2). That is, the larger the value of Wad, the smaller the crack propagation velocity of the interface. Therefore, it can be predicted that an alloying element with a large Wad value will reduce the brittle crack propagation velocity of the Ni/Ni3Al interface. Moreover, the value of Wad increases with the increasing atomic concentration of Re or W, but decreases for Co. This indicates that at low temperature Re and W can inhibit brittle crack propagation of the Ni/Ni3Al interface, and W has the greatest effect, while Co can accelerate interface crack propagation, which agrees well with the results discussed in Section 3.2.2.
| System | Wad (J m−2) | |
|---|---|---|
| Ni/Ni3Al | 3.016 | |
| Ni(Re)/Ni3Al | 1 at% Re | 3.038 |
| 2 at% Re | 3.059 | |
| Ni(Co)/Ni3Al | 1 at% Co | 3.013 |
| 2 at% Co | 3.009 | |
| Ni(W)/Ni3Al | 1 at% W | 3.056 |
| 2 at% W | 3.097 |
3.3 Influence of alloying element on the crack propagation at high temperature
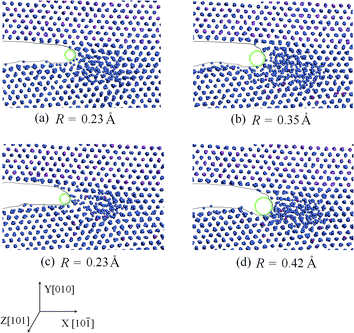
To investigate the influence of the alloying element on the crack propagation of the Ni/Ni3Al interface at high temperature, we gave the crack-tip shapes at 1273 K. The surface energy and unstable stacking energy were calculated to evaluate the competition between crack cleavage and dislocation emission at the crack tip.![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 1 × 109 s−1 at 1273 K. From Fig. 6, at high temperature the cracks advance in a ductile manner in the Ni matrix, which is consistent with experiments,24–26 and the crack tips become blunt with the addition of the alloying elements.
= 1 × 109 s−1 at 1273 K. From Fig. 6, at high temperature the cracks advance in a ductile manner in the Ni matrix, which is consistent with experiments,24–26 and the crack tips become blunt with the addition of the alloying elements.
In this section, to evaluate the bluntness of crack tip, the curvature radius (R) was given by drawing an inscribed circle at the crack tip. The curvature radius of the crack tip increases when adding 2 at% Re (R = 0.35 Å in Fig. 6(b)) or W (R = 0.42 Å in Fig. 6(d)). However, when adding 2 at% Co (R = 0.23 Å in Fig. 6(c)), the curvature radius is the same as without alloying element addition (R = 0.23 Å in Fig. 6(a)). This may be because the Ni–Re and Ni–W bonds are stronger than the Ni–Ni bond while the Ni–Co bond is weaker, which will be confirmed in Section 3.4. The larger curvature radius means that bond breaking of the crack tip is more difficult and the dislocation emission near the crack tip becomes easy. Obviously, the above discussion shows that Re and W can prevent the bond breaking in the cleavage plane. Furthermore, W has the greatest strengthening effect on the interface crack at high temperature.
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 1 × 109 s−1. When 2 at% W atoms were added in the Ni matrix, the a/6〈112〉{111} partial dislocation appeared near the crack tip at 45 ps (as shown by the red atoms in Fig. 7), while at the same time there was no dislocation with the addition of 2 at% Re or Co. This reveals that dislocation emission becomes easy with the addition of W atoms at high temperature.
= 1 × 109 s−1. When 2 at% W atoms were added in the Ni matrix, the a/6〈112〉{111} partial dislocation appeared near the crack tip at 45 ps (as shown by the red atoms in Fig. 7), while at the same time there was no dislocation with the addition of 2 at% Re or Co. This reveals that dislocation emission becomes easy with the addition of W atoms at high temperature.
The crack propagates in the Ni matrix at high temperature, as shown in Fig. 6, and γs for the (100) plane of the Ni matrix was calculated using the MD method. The calculation model contained 240![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms, including 200 atomic layers along the x[10
000 atoms, including 200 atomic layers along the x[10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] direction, 80 atomic layers along the y[010] direction, and 60 atomic layers along the z[101] direction. The surface energy γs is defined as12,38
] direction, 80 atomic layers along the y[010] direction, and 60 atomic layers along the z[101] direction. The surface energy γs is defined as12,38
| γs = (Eoff − Eon)/(2S) | (2) |
Table 4 lists the calculated values of γs for the systems with and without alloying element X (X = Re, Co, or W) in the Ni matrix. Compared with the pure Ni matrix, the value of γs increases with the addition of Re or W atoms, and decreases with the addition of Co atoms. Moreover, the higher the concentration of Re or W atoms, the larger the value of γs, while the opposite trend is observed for Co. For example, the calculated values of γs with 1 and 2 at% Re atoms were 1.602 and 1.616 J m−2, while for Co they were 1.589 and 1.586 J m−2, respectively. Comparing the values of γs for the same concentrations of Re and W atoms, W has a greatest effect on the surface energy, which may be related to the strengths of the Ni–X bonds, which will be discussed in Section 3.4.
The energy barrier for partial dislocation nucleation can be approximately evaluated by the unstable stacking energy (γμs), which was introduced by Rice.37 As shown in Fig. 7, the a/6〈112〉 Shockley partial dislocation occurs in the Ni matrix with the addition of alloying element W. Here, the γμs values of the a/6〈112〉 Shockley partial dislocation for the systems with and without X (X = Re, Co, or W) atoms were calculated by the MD method. The simulation model included 201![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 atoms, with 168 atomic layers along the x[112] direction, 120 atomic layers along the y[11
600 atoms, with 168 atomic layers along the x[112] direction, 120 atomic layers along the y[11![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] direction, and 60 atomic layers along the z[
] direction, and 60 atomic layers along the z[![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10] direction. Periodic boundary conditions were applied in the x and z directions, and a free boundary condition was used in the y direction. The simulation model was divided into two equal parts by the (11
10] direction. Periodic boundary conditions were applied in the x and z directions, and a free boundary condition was used in the y direction. The simulation model was divided into two equal parts by the (11![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) plane: the lower half part was fixed and the upper half part was gradually slipped along the [112] direction in the (11
) plane: the lower half part was fixed and the upper half part was gradually slipped along the [112] direction in the (11![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) plane. Then, the relative energy difference of the system before and after slipping was calculated by12,39
) plane. Then, the relative energy difference of the system before and after slipping was calculated by12,39
| EPOT(R,0) = (EPOT(R) − EPOT(0))/S | (3) |
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) plane. When R = 0.5b (b is the magnitude of the Burgers vector of the a/6[112] Shockley partial dislocation), the γμs of the system can be approximately obtained.
) plane. When R = 0.5b (b is the magnitude of the Burgers vector of the a/6[112] Shockley partial dislocation), the γμs of the system can be approximately obtained.
Table 4 lists the calculated γμs values for the systems with (1 and 2 at%) and without X (X = Re, Co, or W) atoms. From Table 4, the value of γμs decreases with the addition of alloying elements, and the higher the concentration of X atoms, the lower the values of γμs. The ratio of γs/γμs is also listed in Table 4. The γs/γμs ratios all increase when 1 or 2 at% X (X = Re, Co, or W) atoms are randomly doped into the Ni matrix. As an example, the γs/γμs ratio increases by 2.06%, 0.93%, and 14.73% with the addition of 2 at% Re, Co, and W, respectively. This reveals that at high temperature, dislocation emission becomes much easier and cleavage is more difficult when alloying atoms are randomly doped into the pure Ni matrix. Doping with W results in the largest increase of γs/γμs, which suggests that the dislocation more easily occurs with the addition of W atoms than with Re or Co atoms. This was confirmed in Section 3.3.2. Moreover, the a/6〈112〉 Shockley partial dislocation occurs in the Ni matrix with 6 at% Re (or Co) addition at 45 ps, which is consistent with a previous study.12 Accordingly, we predict that a dislocation will occur in the Ni matrix of a Ni/Ni3Al interface system with a large γs/γμs ratio when doped with an appropriate amount of an alloying element.
3.4 Bonding strength of Ni–X (X = Re, Co, or W)
From the above results, the effects of the three alloying elements Re, Co, and W on the crack propagation of the Ni/Ni3Al interface at low or high temperature are different. The reason may be related to the interatomic interactions of Ni–X (X = Re, Co, or W). Thus, it is necessary to calculate and compare the bonding strengths of Ni–X and Ni–Ni.
 | (4) |
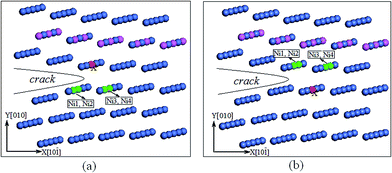
Because both the upper and lower crack surfaces consist of Ni atomic layers, we only considered the interatomic energies between alloying element X (X = Re, Co, or W) and Ni atoms. First, two interface crack models were constructed to calculate the IE: one with X on the upper surface of the crack tip (Fig. 9(a)) and the other with X on the lower surface (Fig. 9(b)). Both of the crack models consisted of 8000 atoms, with 20 atomic layers along the z[101] direction and 40 atomic layers along the x[10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] and y[010] directions. The alloying X (X = Re, Co, or W) atom was at the center of the crack tip along the crack front. Then, each model was relaxed by MD simulation with the Ni–Al–X (X = Re, Co, or W) EAM potential.13–15 Finally, a cluster containing 150 atoms located at the crack tip of the Ni/Ni3Al interface was selected to perform the DVM calculation. Here, spin-polarization calculations were performed, and more calculation details of the IE can be found in the literature.45,48
] and y[010] directions. The alloying X (X = Re, Co, or W) atom was at the center of the crack tip along the crack front. Then, each model was relaxed by MD simulation with the Ni–Al–X (X = Re, Co, or W) EAM potential.13–15 Finally, a cluster containing 150 atoms located at the crack tip of the Ni/Ni3Al interface was selected to perform the DVM calculation. Here, spin-polarization calculations were performed, and more calculation details of the IE can be found in the literature.45,48
Fig. 10 shows the absolute values of the IE between alloying atom X (X = Re, Co, or W) and its four nearest-neighbor atoms. In Fig. 10(a) and (b), the absolute values of IE between Re (or W) and the four nearest-neighbor atoms (Ni1–Ni4) are all larger than that of Ni–Ni. Ni–W has the largest absolute value of IE, which is more than three times larger than the IE of Ni–Ni. This reveals that there is a stronger bond between Re (and W) and Ni atoms than between Ni atoms, and the Ni–W bond is the strongest. Co exhibits the smallest absolute IE with Ni1–Ni4, which is even less than the IE of Ni–Ni. This suggests that there is a weaker bond between Co and Ni atoms than between Ni and Ni atoms. From Fig. 10, the order of the interaction between alloying atom X (X = Re, Co, or W) and Ni atoms in the Ni/Ni3Al interface crack is W > Re > Co, which agrees with the result from the well depth of the pair potential, as discussed in Section 3.4.1.
From the above discussion, we can conclude that the Ni–Re and Ni–W bonds are indeed stronger than Ni–Ni. Therefore, at low temperature, Re and W can prevent brittle propagation of the Ni/Ni3Al interface crack, while at high temperature the crack tip becomes blunter with the addition of Re or W atoms. In contrast, the trend for Co is the opposite because the Co–Ni bond is weaker than the Ni–Ni bond. Moreover, W forms the strongest bonds with Ni atoms. Thus, at high temperature dislocation begins to appear from the crack tip with 2 at% W doping in the Ni matrix.
4. Conclusions
In summary, the Ni/Ni3Al interface crack at the (010)[101] orientation was constructed to investigate the influence of the alloying elements Re, Co, and W on the propagation of the interface crack at low and high temperatures. The results are as follows:(1) The alloying elements Re and W can improve the mechanical properties of superalloys. Moreover, the calculated results, such as the ratio of G/B and Poisson's ratio ν, show that Re and W can increase the ductility of superalloys at high temperature, and W has a greater effect than Re.
(2) The Ni/Ni3Al interface crack propagates in a brittle manner at low temperature, but in a ductile manner at high temperature, both with and without the addition of alloying elements.
(3) The alloying elements Re and W can restrict brittle propagation of the Ni/Ni3Al interface crack because Ni–Re and Ni–W bonds are stronger than Ni–Ni bonds. This means that Re and W can decrease the brittleness of superalloys, and W has a greater effect. Moreover, the propagation velocity of the brittle crack is inversely proportional to the adhesion work of interface, which can be used to predict that an alloying element with large Wad is able to prevent brittle crack propagation.
(4) At high temperature, the crack tip of the Ni/Ni3Al interface becomes blunt with the addition of Re or W atoms, and dislocation occurs near the crack tip when 2 at% W atoms are added. This reveals that the alloying elements Re and W can improve the ductility of superalloys at high temperature, and W has the greater effect.
(5) The competition between cleavage and dislocation emission of the interface crack can be evaluated by the ratio γs/γμs, the higher the ratio, the easier dislocation emission and the more difficult cleavage.
Acknowledgements
This work was supported by the National Basic Research Program of China (Grant no. 2011CB606402) and the National Natural Science Foundation of China (Grant no. 51071091). The simulations were performed using the “Explorer 100” cluster system at Tsinghua National Laboratory for Information Science and Technology, Beijing, China.References
- R. C. Reed, The Superalloys: Fundamentals and Applications, Cambridge University Press, Cambridge, 2006 Search PubMed.
- S. Tin, L. Zhang, R. A. Hobbs, A. C. Yeh, C. M. F. Rae and B. Broomfield, in Superalloys 2008,Proceedings of the Eleventh International Symposium on Superalloys, The Minerals, Metals and Materials Society, Warrendale, 2008, p. 81 Search PubMed.
- J. X. Zhang, T. Murakumo, Y. Koizumi, H. Harada and S. Masaki, Metall. Mater. Trans. A, 2002, 3, 3741 CrossRef PubMed.
- H. Harada and H. Murakami, Springer Series in Materials Science, Springer, Berlin, 1999, vol. 34, p. 39 Search PubMed.
- J. G. Yu, Q. X. Zhang, R. Liu, Z. F. Yue, M. K. Tang and X. W. Li, RSC Adv., 2014, 4, 32749 RSC.
- K. Chen, L. R. Zhao and J. S. Tse, Mater. Sci. Eng., A, 2004, 365, 80 CrossRef PubMed.
- K. Chen, L. R. Zhao and J. S. Tse, Mater. Sci. Eng., A, 2003, 360, 197 CrossRef.
- X. F. Gong, G. X. Yang, Y. H. Fu, Y. Q. Xie, J. Zhuang and X. J. Ning, Comput. Mater. Sci., 2009, 47, 320 CrossRef CAS PubMed.
- P. Peng, A. K. Soh, R. Yang and Z. Q. Hu, Comput. Mater. Sci., 2006, 38, 354 CrossRef CAS PubMed.
- C. Wang and C. Y. Wang, Surf. Sci., 2008, 602, 2604 CrossRef CAS PubMed.
- L. Peng, P. Peng, Y. G. Liu, S. He, H. Wei, T. Jin and Z. Q. Hu, Comput. Mater. Sci., 2012, 63, 292 CrossRef CAS PubMed.
- Z. G. Liu, C. Y. Wang and T. Yu, Modell. Simul. Mater. Sci. Eng., 2013, 21, 045009 CrossRef.
- J. P. Du, C. Y. Wang and T. Yu, Modell. Simul. Mater. Sci. Eng., 2013, 21, 015007 CrossRef.
- J. P. Du, C. Y. Wang and T. Yu, Chin. Phys. B, 2014, 23, 033401 CrossRef.
- Q. N. Fan, C. Y. Wang, T. Yu and J. P. Du, Phys. B, 2015, 456, 283 CrossRef CAS PubMed.
- A. D. Celel and D. N. Duhl, Second-generation nickel-base single crystal superalloy, Superalloys, 1988, 235 Search PubMed.
- K. Chen, L. R. Zhao and J. S. Tse, Philos. Mag., 2003, 83, 1685 CrossRef CAS PubMed.
- W. Z. Wang and T. Jin, Mater. Sci. Eng., A, 2008, 479, 148 CrossRef PubMed.
- Y. Amouyal, Z. Mao and C. Booth-Morrison, et al., Appl. Phys. Lett., 2009, 94, 041917 CrossRef PubMed.
- Z. Suo, Proc. R. Soc. London, Ser. A, 1990, 427, 331 CrossRef CAS.
- A. Volek, F. Pyczak, R. F. Singer and H. Mughrabi, Scr. Mater., 2005, 52, 141 CrossRef CAS PubMed.
- R. C. Reed, A. C. Yeh, S. Tin, S. S. Babu and M. K. Miller, Scr. Mater., 2004, 51, 327 CrossRef CAS PubMed.
- R. Srinivasan, R. Banerjee, J. Y. Hwang, G. B. Viswanathan, J. Tiley, D. M. Dimiduk and H. L. Fraser, Phys. Rev. Lett., 2009, 102, 086101 CrossRef CAS.
- F. Schubert, T. Rieck and P. J. Ennis, in Proceedings of the Ninth International Symposium on Superalloys, TMS, Warrendale, 2000, p. 314 Search PubMed.
- M. B. Henderson and J. W. Martin, Acta Mater., 1996, 44, 111 CrossRef CAS.
- M. Ott and H. Mughrabi, Mater. Sci. Eng., A, 1999, 272, 24 CrossRef.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, Oxford, 1987, p. 83 Search PubMed.
- J. Rifkin, Center for Simulation, University of Connecticut, CT, (http://xmd.sourceforge.net/) Search PubMed.
- R. Hill, Proc. Phys. Soc., London, 1952, 65, 349 CrossRef.
- G. Grimvall, Thermophysical properties of materials, North-Holland, Amsterdam, 1999 Search PubMed.
- Y. Mishin, Acta Mater., 2004, 52, 1451 CrossRef CAS PubMed.
- G. Simmons and H. Wang, Single Crystal Elastic Constants and Calculated Aggregate Properties, MIT Press, Cambridge, 1971 Search PubMed.
- Y. J. Wang and C. Y. Wang, Philos. Mag., 2009, 89, 2935 CrossRef CAS PubMed.
- Y. J. Wang and C. Y. Wang, Mater. Res. Soc. Symp. Proc., 2009, 1224, FF05 CrossRef PubMed.
- M. W. Finnis, J. Phys.: Condens. Matter, 1996, 8, 5811 CrossRef CAS.
- C. Wang and C. Y. Wang, Appl. Surf. Sci., 2009, 255, 3669 CrossRef CAS PubMed.
- J. R. Rice, J. Mech. Phys. Solids, 1992, 40, 239 CrossRef CAS.
- S. L. Liu, C. Y. Wang, T. Yu and Z. G. Liu, Comput. Mater. Sci., 2015, 97, 102 CrossRef CAS PubMed.
- H. X. Xie, C. Y. Wang and T. Yu, J. Mater. Res., 2008, 23, 1597 CrossRef CAS.
- P. A. Gordon and T. Neeraj, Acta Mater., 2009, 57, 3091–3100 CrossRef CAS PubMed.
- S. Y. Wang, C. Y. Wang, J. H. Sun, W. H. Duan and D. L. Zhao, Phys. Rev. B, 2001, 65, 035101 CrossRef.
- Z. G. Liu, C. Y. Wang and T. Yu, Comput. Mater. Sci., 2014, 83, 196 CrossRef CAS PubMed.
- C. Y. Wang and D. L. Zhao, Mater. Res. Soc. Symp. Proc., 1994, 318, 571 CrossRef CAS.
- C. Y. Wang, Acta Metall. Sin., 1997, 33, 54 CAS.
- F. H. Wang and C. Y. Wang, Phys. Rev. B, 1998, 57, 289 CrossRef CAS.
- D. E. Ellis, G. A. Benesh and E. Byrom, Phys. Rev. B, 1977, 16, 3308 CrossRef CAS.
- D. Guenzburger and D. E. Ellis, Phys. Rev. B, 1992, 45, 285 CrossRef CAS.
- Z. Z. Chen and C. Y. Wang, Phys. Rev. B, 2005, 72, 104101 CrossRef.
| This journal is © The Royal Society of Chemistry 2015 |