Electronic structures of two types of TiO2 electrodes: inverse opal and nanoparticulate cases
Abstract
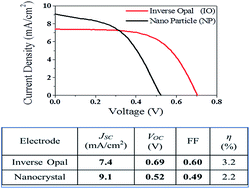
We present a comparison between the electronic structures of inverse opal (IO) and nanoparticulate (NP)-TiO2 electrodes. The electronic structure details were obtained from optical absorption, fluorescence, and valence band studies in order to clarify the nature of the higher photovoltaic performance observed in sensitized solar cells using IO-TiO2 electrodes. We used photoacoustic (PA) and photoluminescence (PL) spectroscopy to characterize the optical absorption and fluorescence properties, respectively. Photoelectron yield (PY) spectroscopy was applied to characterize the position of the valence band maximum (VBM) of the IO- and NP-TiO2 electrodes. The PA spectrum for IO-TiO2 is different to that for NP-TiO2, indicating differences in the exciton–phonon interactions and the density of states in the conduction band. PL measurements showed that the curvature of the valence band structure of IO-TiO2 is different to that of NP-TiO2. Also, PL measurements showed that the oxygen vacancy in IO-TiO2 is different to that in NP-TiO2. Moreover, PY measurements showed VBM in IO-TiO2 to be at a higher position than that in NP-TiO2, suggesting a correlation with the increased open circuit voltage (Voc) in sensitized solar cells.

 Please wait while we load your content...
Please wait while we load your content...