Improved magnetic damping in CoFeB|MgO with an N-doped Ta underlayer investigated using the Brillouin light scattering technique
Abstract
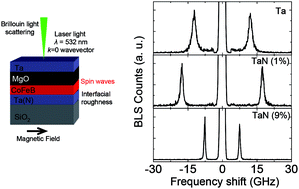
Understanding the role of interfacial roughness on magnetic damping is important for developing advanced spintronic based devices. Using Brillouin light scattering (BLS), here we investigate the interfacial roughness contributing to magnetic inhomogeneity in the technologically important ultrathin CoFeB|MgO heterostructures with Ta and N-doped Ta underlayers. The spin wave frequencies corresponding to uniform precession modes in the BLS spectra for perpendicularly magnetized as well as in-plane magnetized films are investigated. The linewidth shows pronounced dependence on the N-doping in the underlayer. The analysis of linewidth suggests that the magnetic inhomogeneity and the damping reduce significantly by N-doping in the underlayer.

 Please wait while we load your content...
Please wait while we load your content...