Aluminum interaction with 2,3-diphosphoglyceric acid. A computational study†
Noelia Luque,
Jon I. Mujika,
Elena Formoso and
Xabier Lopez*
Kimika Fakultatea, Euskal Herriko Unibertsitatea UPV/EHU, Donostia International Physics Center (DIPC), P. K. 1072, 20080 Donostia, Euskadi, Spain. E-mail: xabier.lopez@ehu.es
First published on 3rd July 2015
Abstract
The interaction of aluminum with 2,3-diphosphoglyceric acid (2,3-DPG) is thought to be one of the strongest interactions of aluminium with a biophosphate molecule. In this article, the affinity energies for a family of Al–(2,3-DPG) complexes are calculated at the DFT level of theory. The study includes a total of 26 structures that vary from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes, to 1
1 complexes, to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 stoichiometry and ternary complexes with citrate, considering different coordination modes and protonation states. Our results demonstrate that in the case of 1
2 stoichiometry and ternary complexes with citrate, considering different coordination modes and protonation states. Our results demonstrate that in the case of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes, the 2,3-DPG ligand could compete with citrate for complexation with aluminum at physiological pH. However, for the rest of the complexes there is a clear preference for Al(Citr)2 > Al(2,3-DPG)(Citr) ternary complex > Al(2,3-DPG)2 complexes. For each of these groups the charge of the ligand determines the affinity but to a lower extent than the nature of the Citr/2,3-DPG ligands. In summary, our results point to a high variety of possible complexation modes of 2,3-DPG to aluminum, showing a higher preference towards the formation of ternary complexes.
1 complexes, the 2,3-DPG ligand could compete with citrate for complexation with aluminum at physiological pH. However, for the rest of the complexes there is a clear preference for Al(Citr)2 > Al(2,3-DPG)(Citr) ternary complex > Al(2,3-DPG)2 complexes. For each of these groups the charge of the ligand determines the affinity but to a lower extent than the nature of the Citr/2,3-DPG ligands. In summary, our results point to a high variety of possible complexation modes of 2,3-DPG to aluminum, showing a higher preference towards the formation of ternary complexes.
1 Introduction
Aluminum, the most abundant metal in the earth’s crust, has largely been excluded from biochemical evolution because of its efficient cycling within the lithosphere.1,2 However, human intervention (soil acidification, food additives, pharmaceuticals, Al-containers, water treatment, etc.) has increased the availability of biologically reactive aluminum,2 and its presence in our bodies has been linked to various human diseases.3–5 Unfortunately, the molecular basis for aluminum toxicity is still poorly understood. A first step to understand the biochemistry of aluminum is to determine the coordination chemistry of aluminum with those biomolecules that are more prone to interact with it.6,7 However, this is a difficult issue due to the complexity and variety of species that aluminum can form in solution, its low solubility and the difficulty to attain thermodynamic equilibrium due to the slow ligand exchange rate.Aluminum as a strong Lewis acid, shows a strong preference for binding negatively-charged oxygen atoms. In fact, citrate, which contains three carboxylates and one alcohol group (Fig. 1), is recognized as the main aluminium low-molecular-mass chelator in blood serum.8 On the other hand, molecules containing phosphate groups are also a likely target for interacting with the cation.9–11 Due to the variety of cellular processes in which molecules containing phosphate groups are present (ATP, phosphorylated proteins, DNA, RNA, etc.), this high affinity to form Al(III)–phosphate compounds could disrupt key processes of the cell metabolism. In fact, aluminum is able to cross the blood brain barrier and reach the nucleus of neurons,4,5,12 binding to nuclear chromatin and disrupting the transcription of genetic information.10,13 Besides, the ability of aluminum to enhance neurofibrilary tangle formation14 through the stabilization of phosphorylated tau protein is well known.15 In this vein, aluminum has been recognized as a neurotoxic compound.16
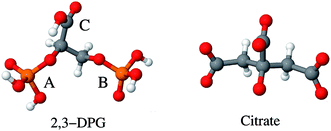 | ||
| Fig. 1 The two aluminum ligands employed in this study: 2,3-diphosphoglyceric acid (2,3-DPG) and citrate. Note that 2,3-DPG is presented in its neutral protonation state. | ||
The toxicity of aluminum has been linked to various ill-conditions, among them anaemia. It is known that prolonged elevated doses of aluminum exposure contribute to the microcytic hypochromic anemia.17–19 The cause for aluminum induced anaemia is uncertain: the iron levels are normal, but the red blood cells are reduced in size (microcytosis). Aluminium is known to affect the erythrocyte membrane integrity20,21 and lowers haemoglobin levels interfering with the haemoglobin synthesis. 2,3-DPG is an important constituent of red cells, present at a 2–4 mM concentration, and besides ATP, has been proposed to be the predominant small molecule binder in red cells. The interaction of aluminum with 2,3-DPG could play an important role to transport aluminum from the plasma to the inside of red cells. The amount of 2,3-DPG considerably exceeds haemoglobin, and even though the Al(III) interaction with 2,3-DPG is strong, the aluminum levels are probably not high enough to withdraw significant quantities of 2,3-DPG from interacting with haemoglobin. However, a 2,3-DPG complex of aluminum may become an active toxic species and therefore the characterization of the possible species to be formed, the preferential coordination modes and binding affinity are of high interest.
Theoretical calculations can help to shed light on the different aluminum-complexes formed in aqueous solution at equilibrium22–33 and non-equilibrium34,35 regimes. In this sense, we have recently been able to provide the first consistent theoretical binding map of Al(III) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexation with phosphates,36 which allowed determination of the relative affinity of aluminum towards different structural phosphate motifs. Thus, we characterized the coordination chemistry of around 60 phosphates to aluminum, including in our dataset various types of biologically relevant phosphates with different degrees of esterification, charge, and number of phosphate units. Our calculations reveal important trends in the intrinsic affinity of aluminum for different types of phosphate, finding that the strongest interaction occurs for ATP-like triphosphates, phosphate monoesters, and highly-charged bisphosphates. In this sense, molecules such as 2,3-diphosphateglycerate, also called 2,3-bisphosphoglycerate (2,3-DPG presented in Fig. 1), are ideal candidates for aluminum chelation. This potential aluminum binder is present at high concentrations in red cells, and has been proposed37 to be the predominant small ligand chelator of aluminum inside red cells. Thus, the formation of Al–(2,3-DPG) species could then lead to harmful species, and be the basis of toxic effects of aluminum, such as aluminum-induced anaemia.
1 complexation with phosphates,36 which allowed determination of the relative affinity of aluminum towards different structural phosphate motifs. Thus, we characterized the coordination chemistry of around 60 phosphates to aluminum, including in our dataset various types of biologically relevant phosphates with different degrees of esterification, charge, and number of phosphate units. Our calculations reveal important trends in the intrinsic affinity of aluminum for different types of phosphate, finding that the strongest interaction occurs for ATP-like triphosphates, phosphate monoesters, and highly-charged bisphosphates. In this sense, molecules such as 2,3-diphosphateglycerate, also called 2,3-bisphosphoglycerate (2,3-DPG presented in Fig. 1), are ideal candidates for aluminum chelation. This potential aluminum binder is present at high concentrations in red cells, and has been proposed37 to be the predominant small ligand chelator of aluminum inside red cells. Thus, the formation of Al–(2,3-DPG) species could then lead to harmful species, and be the basis of toxic effects of aluminum, such as aluminum-induced anaemia.
In the present manuscript, we use density functional theory in its B3LYP form to characterize 26 Al–(2,3-DPG) complexes which vary in the type of coordination, total charge, and ligand/aluminum ratio. The high affinity of aluminum for 2,3-DPG is confirmed, similar to the one for ATP (a known biophosphate Al(III) binder), and a diversity of possible competing compounds in solution is identified. In the case of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes the affinities are such that 2,3-DPG could compete with citrate for aluminum binding at physiological pH. However, the incorporation of a second 2,3-DPG to the aluminum coordination sphere is less likely than the formation of ternary compounds with citrate. With an excess of citrate, Al(Cit)2 formation would be favored, so that citrate could have the potential to withdraw aluminium from interacting with 2,3-DPG.
1 complexes the affinities are such that 2,3-DPG could compete with citrate for aluminum binding at physiological pH. However, the incorporation of a second 2,3-DPG to the aluminum coordination sphere is less likely than the formation of ternary compounds with citrate. With an excess of citrate, Al(Cit)2 formation would be favored, so that citrate could have the potential to withdraw aluminium from interacting with 2,3-DPG.
2 Methods
2.1 Density functional theory calculations
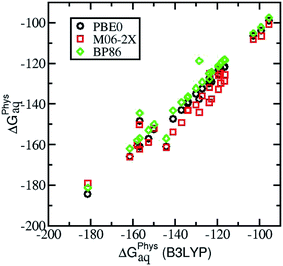
All geometrical optimizations were carried out in aqueous phase using the Gaussian 09 program,38 B3LYP functional39–42 and 6-31++G(d,p) basis set. To confirm that the optimized structures were real minima on the potential energy surfaces, frequency calculations were carried out at the same level of theory. All structures showed positive force constants for all the normal modes of vibration. The frequencies were then used to evaluate the zero-point vibrational energy (ZPVE) and the thermal (T = 298 K) vibrational corrections to the enthalpies and Gibbs free energies within the harmonic oscillator approximation. To calculate the entropy, the different contributions to the partition function were evaluated using the standard statistical mechanics expressions in the canonical ensemble and the harmonic oscillator and rigid rotor approximation. The solvent effect was introduced using the self-consistent reaction field (SCRF) method with the polarized continuum model (PCM), using the integral equation formalism variant (IEFPCM).43 The electronic energies were refined by single-point energy calculations at the B3LYP/6-311++G(3df,2p) level of theory. To confirm the adequacy of the methodology, we re-evaluated the affinity energies by single-point calculations with three different functionals: PBE0, BP86 and M062-X. Although B3LYP tends to underestimate the ligand binding affinities, the trends in binding affinity are equally described by the different functionals (see Fig. 2). Results with different functionals can be found in the ESI.†2.2 Binding free energies in solution
We studied three different types of complexes: the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 aluminum–2,3-DPG structures and the 1
2 aluminum–2,3-DPG structures and the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ternary complexes by Al(III), 2,3-DPG and citrate. The 1
1 ternary complexes by Al(III), 2,3-DPG and citrate. The 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex formation stability was studied following the ligand substitution reaction shown in (1):
1 complex formation stability was studied following the ligand substitution reaction shown in (1):| [Al(H2O)6](aq,1 M)3+ + L(aq,1 M)q− → [Al(H2O)6−mL](aq,1 M)3−q + mH2O(aq,1 M) | (1) |
ΔHcomplaq = Haq(Al(H2O)6−mL) + mHaq(H2O) − Haq(Al(H2O)6) − Haq(L) + ΔnRT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(24.46) ln(24.46)
| (2) |
Since the enthalpies are determined using an ideal gas at 1 atm as the standard state, the last term in eqn (2) corresponds to the volume change due to the transformation from 1 atm to 1 M in solution, where Δn refers to the change in the number of species in the reaction.44 In a similar way, the free energy of the complexes is determined as:
ΔGcomplaq = Gaq(Al(H2O)6−mL) + mGaq(H2O) − Gaq(Al(H2O)6) − Gaq(L) + ΔnRT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(24.46) + mRT(ln ln(24.46) + mRT(ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55.34) 55.34)
| (3) |
In the case of the second substitution for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 or ternary complexes, the considered substitution equation is as follows:
2 or ternary complexes, the considered substitution equation is as follows:
| [Al(H2O)6](aq,1 M)3+ + L(aq,1 M)q− + M(aq,1 M)r− → [Al(H2O)6−mLM](aq,1 M)3−q−r + mH2O(aq,1 M) | (4) |
The enthalpy and free energy in solution corresponding to the binding of the ligand in these last two cases are coherent with eqn (2) and (3) with the corresponding changes.
The pKa values for 2,3-DPG are 3.32, 6.09 and 7.27,37 for the carboxylic acid, the 3-phosphate and the 2-phosphate, respectively (C, B and A groups in Fig. 1) and the values for citric acid are 3.09, 4.75 and 5.41.45 The pKa values of all titratable groups of citrate were computed previously,46 and the value of the alcohol group drops from 11.6 in solution to 5.4 when interacting with Al(III), because the acidity of the ligand changes upon its coordination to Al(III). Thus, the OH group of the citrate is considered protonated in solution under physiological conditions, but deprotonated when coordinated to Al(III). In eqn (2) and (3) the same protonation state was considered for citrate in solution and coordinated to Al(III), therefore a correction must be introduced for those complexes where citrate is involved:
| ΔGdeprot = 2.303RT(pKa − pH) | (5) |
In the case of 2,3-DPG, we consider some of the complexes with the ligand protonated. In such cases the three pKa values stated above (3.32, 6.09 and 7.27) were considered to evaluate the protonation energy as:
| ΔGprot = 2.303RT(pH − pKa) | (6) |
The final free energy at physiological pH values (ΔGPhysaq) for all compounds is therefore evaluated as:
| ΔGPhysaq = ΔGcomplaq + ΔGdeprotaq or ΔGPhysaq = ΔGcomplaq + ΔGprotaq | (7) |
3 Results
There are three potential chelating functional groups in 2,3-DPG: two phosphate groups and a carboxylic group (as illustrated in Fig. 1). In this paper, the two phosphate groups are referred to as A (2-phosphate group) and B (3-phosphate group), and the carboxylic group as C. All three groups present in 2,3-DPG comprise acid oxygens that are able to interact with Al(III). There are two strong acid deprotonation steps, one from each phosphate group. The successive mixed pKa values reported in ref. 37 are 3.32, 6.09 and 7.27, which belong to the glyceric acid group, the 3-phosphate group (B group) and the 2-phosphate group (A group), respectively. Therefore, a big variety of binding modes and protonation states for Al–(2,3-DPG) complexes is possible. A total of 26 compounds were considered here. The affinity energies can be found in Table 1 and Fig. 3. This dataset comprises Al–(2,3-DPG) complexes with different binding modes and various total charges (−1, −2, −5, −6, −7). We can classify these complexes in three different groups: (i) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Al–(2,3-DPG) complexes, (ii) 1
1 Al–(2,3-DPG) complexes, (ii) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 Al–(2,3-DPG)2 complexes and (iii) ternary Al–(2,3-DPG)(Citr) complexes. We have also determined the complexation energies of aluminum with citrate in the 1
2 Al–(2,3-DPG)2 complexes and (iii) ternary Al–(2,3-DPG)(Citr) complexes. We have also determined the complexation energies of aluminum with citrate in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Al–Citr and 1
1 Al–Citr and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 Al–Citr2 complexes for comparison.
2 Al–Citr2 complexes for comparison.
| Structure | ΔHcomplaq | ΔGcomplaq | ΔGPhysaq |
|---|---|---|---|
Complexes 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1 1 |
|||
| [Al(2,3-DPG)AC(H2O)4]2−(‡) | −119.22 | −118.40 | −118.40 |
| [Al(2,3-DPG)bAC(H2O)4]1− | −102.89 | −100.84 | −99.05 |
| [Al(2,3-DPG)BC(H2O)4]2−(‡) | −103.69 | −102.82 | −102.82 |
| [Al(2,3-DPG)aBC(H2O)4]1−(‡) | −96.97 | −95.61 | −95.43 |
| [Al(2,3-DPG)AB(H2O)4]2−(‡) | −119.72 | −119.33 | −119.33 |
| [Al(2,3-DPG)ABC(H2O)3]2− | −118.85 | −123.54 | −123.54 |
| [Al(Citr)(H2O)3]1− | −124.90 | −133.02 | −123.46 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
Complexes 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 2 2 |
|||
| [Al(2,3-DPG)2,AC(H2O)2]7− | −136.19 | −134.01 | −134.01 |
| [Al(2,3-DPG)bb2,AC(H2O)2]5− | −131.94 | −130.64 | −127.06 |
| [Al(2,3-DPG)aa2,AC(H2O)2]5−(‡) | −119.80 | −118.70 | −118.34 |
| [Al(2,3-DPG)ab2,AC(H2O)2]5− | −121.13 | −119.91 | −116.34 |
| [Al(2,3-DPG)b2,AC(H2O)2]6− | −136.68 | −135.45 | −133.66 |
| [Al(2,3-DPG)2,AC*(H2O)2]7− | −131.26 | −130.03 | −130.03 |
| [Al(2,3-DPG)2,AB(H2O)2]7− | −138.05 | −136.85 | −136.85 |
| [Al(2,3-DPG)bb2,AB(H2O)2]5− | −123.99 | −122.94 | −119.36 |
| [Al(2,3-DPG)aa2,AB(H2O)2]5− | −127.15 | −123.01 | −122.66 |
| [Al(2,3-DPG)ab2,AB(H2O)2]5− | −121.47 | −118.52 | −116.56 |
| [Al(2,3-DPG)2,AB*(H2O)2]7− | −142.97 | −140.89 | −140.89 |
| [Al(2,3-DPG)2,AB*,aa(H2O)2]5− | −128.35 | −124.10 | −123.74 |
| [Al(2,3-DPG)2,ABC]7− | −114.11 | −128.43 | −128.43 |
| [Al(Citr)2]5− | −182.65 | −200.39 | −181.28 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
Complexes 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1 1 |
|||
| [Al(2,3-DPG)AC(Citr)(H2O)]6− | −162.75 | −170.94 | −161.39 |
| [Al(2,3-DPG)bAC(Citr)(H2O)]5− | −160.28 | −168.13 | −156.79 |
| [Al(2,3-DPG)AB(Citr)(H2O)]6− | −157.95 | −166.19 | −156.64 |
| [Al(2,3-DPG)bAB(Citr)(H2O)]5− | −147.91 | −155.51 | −144.17 |
| [Al(2,3-DPG)aAB(Citr)(H2O)]5− | −154.38 | −162.25 | −152.52 |
| [Al(2,3-DPG)ABC(Citr)]6− | −150.86 | −167.37 | −157.82 |
| [Al(2,3-DPG)bABC(Citr)]5− | −144.30 | −161.24 | −149.90 |
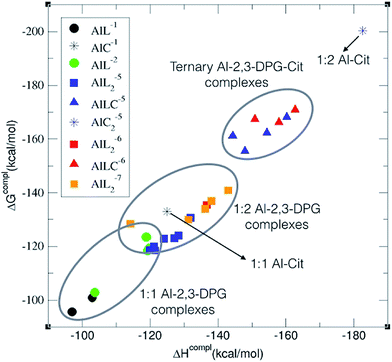
As one can see in Fig. 3, the complexation energies can be clustered in three different zones with affinity energies decreasing in the following order: ternary Al–(2,3-DPG)(Citr) > 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 Al–(2,3-DPG)2 complexes > 1
2 Al–(2,3-DPG)2 complexes > 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Al–(2,3-DPG) complexes. Thus, the inclusion of citrate to form ternary complexes stabilizes the interaction of 2,3-DPG with aluminum. However, in the case of one ligand complexes there is a more competitive situation between citrate and 2,3-DPG for binding aluminum (see below), especially when we consider the deprotonation energy of the citrate alcohol group at physiological pH (ΔGaqPhys column in Table 1). These theoretical results are in line with the high affinity of 2,3-DPG for aluminum previously demonstrated in experimental studies.37,16 In our previous paper,36 we already demonstrated the favorable binding to a bis-phosphate group analogous to the one present in 2,3-DPG, with complexation energies close to the values of an ATP-like triphosphate group.
1 Al–(2,3-DPG) complexes. Thus, the inclusion of citrate to form ternary complexes stabilizes the interaction of 2,3-DPG with aluminum. However, in the case of one ligand complexes there is a more competitive situation between citrate and 2,3-DPG for binding aluminum (see below), especially when we consider the deprotonation energy of the citrate alcohol group at physiological pH (ΔGaqPhys column in Table 1). These theoretical results are in line with the high affinity of 2,3-DPG for aluminum previously demonstrated in experimental studies.37,16 In our previous paper,36 we already demonstrated the favorable binding to a bis-phosphate group analogous to the one present in 2,3-DPG, with complexation energies close to the values of an ATP-like triphosphate group.
It is also remarkable that within each of the three zones in Fig. 3, charge is a driving factor for the binding affinity, obtaining the largest complexation energies for the higher charged compounds. However, this trend is not monotonic and, depending on which complex we compare for the Al–(2,3-DPG)2 and Al–(2,3-DPG)(Citr) cases, we can get the reverse situation. In our previous paper on 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 aluminum–phosphate interaction,36 we clearly found that charge was the main driving force for the ligand binding affinity, but the charges of the complexes were between +3 and −1. In the present paper, for the two ligand complexes we are dealing with complexes of substantially higher charge (−5, −6, −7), and therefore we are reaching the limit of acceptable coulombic repulsion between negative charges. As a consequence, not only charge but a combination of different factors will determine the preferential binding for a given compound.
1 aluminum–phosphate interaction,36 we clearly found that charge was the main driving force for the ligand binding affinity, but the charges of the complexes were between +3 and −1. In the present paper, for the two ligand complexes we are dealing with complexes of substantially higher charge (−5, −6, −7), and therefore we are reaching the limit of acceptable coulombic repulsion between negative charges. As a consequence, not only charge but a combination of different factors will determine the preferential binding for a given compound.
3.1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 1 Al–(2,3-DPG) complexes
1 Al–(2,3-DPG) complexes
Taking into account the different pKa values and the protonation states proposed in ref. 37, six complexes arise as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Al–(2,3-DPG) complexes (see Fig. 4). The first two complexes have the aluminum cation coordinated with the carboxylic group and the A-phosphate group, both of them in a monodentate mode, which we called the AC form. They differ in the protonation state of the B-phosphate group, namely: deprotonated (a) or protonated (b). In the next two structures the phosphates are interchanged so that the groups B and C are coordinated to Al(III), the BC form, with the A-phosphate group deprotonated (c) or protonated (d). In the fifth complex aluminum is coordinated to the two phosphates (e), which is called the AB form, and in the last structure the cation is coordinated to all possible chelating groups (f) and it is called the ABC form. In Table 1 we present the energetics of the substitution reaction for each complex contemplated in this work. Note that in some structures (referred to with the ‡ symbol in Table 1) a spontaneous proton transfer from an Al(III)-bound water molecule to a phosphate group occurred. However, a partial estimation of the energy associated with this proton transfer revealed that its presence does not alter the main qualitative trends in binding affinities outlined in this article (see discussion).
1 Al–(2,3-DPG) complexes (see Fig. 4). The first two complexes have the aluminum cation coordinated with the carboxylic group and the A-phosphate group, both of them in a monodentate mode, which we called the AC form. They differ in the protonation state of the B-phosphate group, namely: deprotonated (a) or protonated (b). In the next two structures the phosphates are interchanged so that the groups B and C are coordinated to Al(III), the BC form, with the A-phosphate group deprotonated (c) or protonated (d). In the fifth complex aluminum is coordinated to the two phosphates (e), which is called the AB form, and in the last structure the cation is coordinated to all possible chelating groups (f) and it is called the ABC form. In Table 1 we present the energetics of the substitution reaction for each complex contemplated in this work. Note that in some structures (referred to with the ‡ symbol in Table 1) a spontaneous proton transfer from an Al(III)-bound water molecule to a phosphate group occurred. However, a partial estimation of the energy associated with this proton transfer revealed that its presence does not alter the main qualitative trends in binding affinities outlined in this article (see discussion).
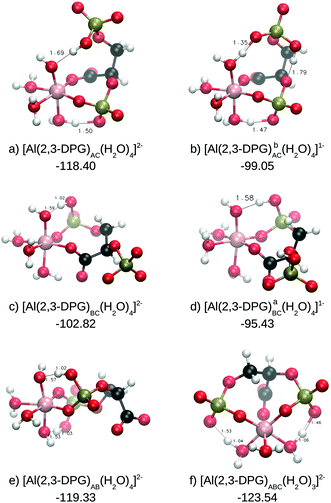 | ||
Fig. 4 Al–(2,3-DPG) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes. The subscripts indicate the coordination mode of 2,3-DPG to Al(III). Their formation energies (ΔGPhysaq) are shown in kcal mol−1. 1 complexes. The subscripts indicate the coordination mode of 2,3-DPG to Al(III). Their formation energies (ΔGPhysaq) are shown in kcal mol−1. | ||
We find similar energetics of the deprotonated ligands (a total charge of −2) in the coordination forms AC, AB and ABC. In the last case, the free energy is more favorable due to the liberation of one more water molecule, which favors the entropy of the system by about 4–5 kcal mol−1 compared to those of the other two complexes. The least favorable complex is the BC form, which has similar energetics in its protonated and deprotonated forms, and is also similar to those of AC in its protonated form. These complexes are about 17 kcal mol−1 less favorable than the others mentioned before. Thus, there is clear preference for interaction with the 2-phosphate group (A-phosphate group) as suggested by Sóvágó et al.,37 with a competition between the 3-phosphate group (B-phosphate group) and acetate to be the second chelating functional group of aluminum. When comparing the complexation energies of these compounds to the one of the Al–Citr complex, we find that they are slightly lower. However, when considering the deprotonation energy of citrate at physiological pH, we obtain very similar ΔGPhysaq for Al–Citr and for Al–(2,3-DPG)ABC. Overall, we can conclude therefore that 2,3-DPG binding is competitive with citrate binding at physiological pH for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes, with three binding modes that are competitive among them: AC, AB and ABC.
1 complexes, with three binding modes that are competitive among them: AC, AB and ABC.
3.2 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 2 Al–(2,3-DPG)2 complexes
2 Al–(2,3-DPG)2 complexes
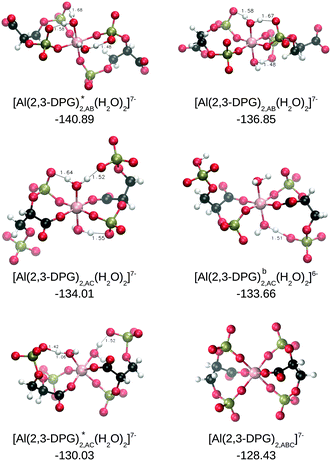
Next, we analyze the energetics corresponding to the complexation of two 2,3-DPG ligands by aluminum (see Fig. 5). We have considered 13 possible compounds that differ in the coordination mode and protonation state of the 2,3-DPG ligand. Based on the results for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes, the 2-phosphate group (A group) coordination is maintained for all complexes. Because of the different protonation states, the resultant total charge of the complexes can be −5, −6 or −7. Due to the highly charged nature of the ligands, the additional second ligand provides only a moderate increase in complexation energies, between 5 to 15 kcal mol−1 (see Table 1). Thus, the complexation free energies for the double ligand incorporation with Al(III) are only moderately higher than those of the 1
1 complexes, the 2-phosphate group (A group) coordination is maintained for all complexes. Because of the different protonation states, the resultant total charge of the complexes can be −5, −6 or −7. Due to the highly charged nature of the ligands, the additional second ligand provides only a moderate increase in complexation energies, between 5 to 15 kcal mol−1 (see Table 1). Thus, the complexation free energies for the double ligand incorporation with Al(III) are only moderately higher than those of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes, with values varying from −116.34 to −140.89 kcal mol−1 for ΔGPhysaq. In terms of coordination modes, there is a slight preference for AB over the AC coordination mode, but the differences are small so that our results would support a mixture of these coordination modes in solution. We found that the tri-coordinated complex is the least stable together with the protonated complexes. Regarding the charge of the ligand, there is an increase in binding with the charge of the system, finding the largest complexation energy for a −7 complex in AB coordination, and the lowest for a −5 complex in AC coordination. However, this trend in higher binding with higher charge is not monotonic, and some of the −7 complexes have lower complexation energies than those of the −6 or −5 complexes.
1 complexes, with values varying from −116.34 to −140.89 kcal mol−1 for ΔGPhysaq. In terms of coordination modes, there is a slight preference for AB over the AC coordination mode, but the differences are small so that our results would support a mixture of these coordination modes in solution. We found that the tri-coordinated complex is the least stable together with the protonated complexes. Regarding the charge of the ligand, there is an increase in binding with the charge of the system, finding the largest complexation energy for a −7 complex in AB coordination, and the lowest for a −5 complex in AC coordination. However, this trend in higher binding with higher charge is not monotonic, and some of the −7 complexes have lower complexation energies than those of the −6 or −5 complexes.
In a previous work, Sóvágó and coworkers37 proposed as a predominant complex an [Al–(2,3-DPG)2,AC]7− complex. Our results partially support that proposal, since this type of complex appears among the ones with the largest affinity.
3.3 Ternary 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 1 Al–(2,3-DPG)(Citr) complexes
1 Al–(2,3-DPG)(Citr) complexes
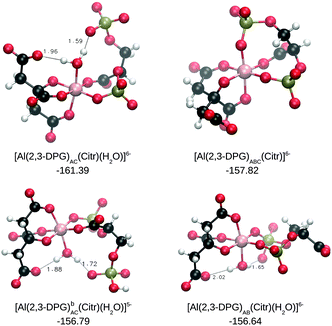
We also considered the possibility of the formation of ternary complexes in the presence of citrate (see Fig. 6). We first started from the three most stable complexes with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry, AC, AB, and ABC complexes and added the citrate ligand. All these 1
1 stoichiometry, AC, AB, and ABC complexes and added the citrate ligand. All these 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes show a very similar complexation enthalpy, namely −119.22, −119.72 and −118.85 kcal mol−1, respectively. When citrate is introduced, they still have similar formation enthalpies, but with differences around 5–12 kcal mol−1 among them (see Table 1). Quite interestingly, in this case there is a slight preference for the AC coordination mode over AB or ABC, with the highest affinity for a −6 complex in the AC binding mode. Again, there is a slight preference for more negatively charged complexes, with −6 complexes having higher complexation energies than those of the −5 ones.
1 complexes show a very similar complexation enthalpy, namely −119.22, −119.72 and −118.85 kcal mol−1, respectively. When citrate is introduced, they still have similar formation enthalpies, but with differences around 5–12 kcal mol−1 among them (see Table 1). Quite interestingly, in this case there is a slight preference for the AC coordination mode over AB or ABC, with the highest affinity for a −6 complex in the AC binding mode. Again, there is a slight preference for more negatively charged complexes, with −6 complexes having higher complexation energies than those of the −5 ones.
It is remarkable that all of the ternary complexes show higher complexation energies (ΔGPhysaq between −144.17 and −161.39 kcal mol−1) than those of the Al–(2,3-DPG)2 species (ΔGPhysaq between −116.34 and −140.89 kcal mol−1). However, all of them are smaller than that of Al–Citr2, even if the deprotonation is taken into account; ΔGPhysaq is −181.28 kcal mol−1. This points to the formation of ternary compounds when both citrate and 2,3-DPG are present in solution. Notice that the existence of ternary compounds has been established48,49 in the context of citrate and phosphate interactions with aluminum. Our prediction is that 2,3-DPG will also be prone to form such complexes.
4 Discussion
In the present paper, using density functional theory, we have characterized 26 of such Al–(2,3-DPG) complexes varying in the type of coordination, total charge, and ligand/aluminum ratio. Our results confirm the high affinity of aluminum to 2,3-DPG, giving rise to a rich speciation chemistry, with various competitive possible species that differ in coordination mode and protonation state. Note that in some of these structures a spontaneous proton transfer from the Al(III)-bound water molecule to a phosphate group takes place. In these structures, the potential energy surfaces corresponding to the proton transfer back to the water molecule were characterized (data not shown). In all cases, the energy difference is in the 5–8 kcal mol−1 range. Thus, even though in some particular cases the relative energy between the two structures could be altered when this correction was included, the difference is small enough to maintain the overall trend shown in Fig. 3.In the case of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes the affinities are such that 2,3-DPG could compete with citrate for aluminum binding at physiological pH. We want to remind you that in the blood plasma, the predominant small molecule aluminum carrier is citrate,24,29,46 while the major protein carrier is transferrin.50–52 Speciation model calculations10 have demonstrated that the free Al(III) concentrations allowed by the most likely Al(III) binders ATP and 2,3-DPG in cells, and citrate and transferrin in blood plasma are about the same. Our results for 1
1 complexes the affinities are such that 2,3-DPG could compete with citrate for aluminum binding at physiological pH. We want to remind you that in the blood plasma, the predominant small molecule aluminum carrier is citrate,24,29,46 while the major protein carrier is transferrin.50–52 Speciation model calculations10 have demonstrated that the free Al(III) concentrations allowed by the most likely Al(III) binders ATP and 2,3-DPG in cells, and citrate and transferrin in blood plasma are about the same. Our results for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes are coherent with this trend for binding affinities. However, at higher concentrations of citrate and 2,3-DPG, where the formation of 1
1 complexes are coherent with this trend for binding affinities. However, at higher concentrations of citrate and 2,3-DPG, where the formation of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and ternary complexes would be predominant, we have shown a preference for citrate binding, either through ternary complexes or by formation of Al(Cit)2. Note that the presence of ternary complexes has been established when phosphates and citrate are present in the solution.48 Moreover, it is known that for ATP comparable concentrations of citrate (in excess with respect to Al) withdraws Al3+ from ATP. The same behaviour is expected for 2,3-DPG, and citrate could act, in this sense, as a protective agent preventing the interaction of Al3+ with 2,3-DPG. In fact, we have recently established a similar protective effect of citrate in the case of the Al3+–α-ketoglutarate interaction.47
2 and ternary complexes would be predominant, we have shown a preference for citrate binding, either through ternary complexes or by formation of Al(Cit)2. Note that the presence of ternary complexes has been established when phosphates and citrate are present in the solution.48 Moreover, it is known that for ATP comparable concentrations of citrate (in excess with respect to Al) withdraws Al3+ from ATP. The same behaviour is expected for 2,3-DPG, and citrate could act, in this sense, as a protective agent preventing the interaction of Al3+ with 2,3-DPG. In fact, we have recently established a similar protective effect of citrate in the case of the Al3+–α-ketoglutarate interaction.47
As for the coordination mode, potentiometric measurements revealed that 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes are formed with Al(III), and complexation most likely occurs at the carboxylate-2-phosphate group chelating site. Our result are coherent with the formation of 1
2 complexes are formed with Al(III), and complexation most likely occurs at the carboxylate-2-phosphate group chelating site. Our result are coherent with the formation of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes and the preferential chelation of the 2-phosphate group. However, for a second chelating group different possibilities could coexist: both chelation to the carboxylate and 3-phosphate groups and even chelation to the three functional groups at the same time. In fact, the geometry seems to be critical in determining the stability of the species, and the higher stability of citrate. Tri-coordinated citrate forms two 5- and 6-membered rings, while a 7-membered ring is the smallest ring that 2,3-DPG can form. To form this ring, the 2-phosphate group must interact with Al(III) and indeed the results predict that this group must be chelated to the cation. On the other hand, the charge born by Al(III) is similar in Al(Cit)2 and the most stable Al–(2,3-DPG)2 species (data not shown), certainly due to the hard acid character of aluminum. This fact indicates therefore that the higher stability provided by citrate is not due to a higher charge transfer to Al(III), but rather due to a better geometrical disposition of the chelating groups.
2 complexes and the preferential chelation of the 2-phosphate group. However, for a second chelating group different possibilities could coexist: both chelation to the carboxylate and 3-phosphate groups and even chelation to the three functional groups at the same time. In fact, the geometry seems to be critical in determining the stability of the species, and the higher stability of citrate. Tri-coordinated citrate forms two 5- and 6-membered rings, while a 7-membered ring is the smallest ring that 2,3-DPG can form. To form this ring, the 2-phosphate group must interact with Al(III) and indeed the results predict that this group must be chelated to the cation. On the other hand, the charge born by Al(III) is similar in Al(Cit)2 and the most stable Al–(2,3-DPG)2 species (data not shown), certainly due to the hard acid character of aluminum. This fact indicates therefore that the higher stability provided by citrate is not due to a higher charge transfer to Al(III), but rather due to a better geometrical disposition of the chelating groups.
Nevertheless, the final outcome will depend on a delicate balance between the relative concentrations of the different ligands (citrate, 2,3-DPG, etc.). For high [Cit] and if all Al(III) is bound to citrate, the Al(Cit)2 species would be clearly predominant. However, for lower citrate concentrations, and in the presence of Al(Cit) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes, the Al(Citr)–2,3-DPG ternary complexes could be formed. Finally, the results predict that Al–2,3-DPG species would only be formed in the absence of citrate. In addition, other factors such as non-equilibrium states and the slow ligand exchange rate of aluminum should be taken into account. Due to this slow rate, intermediate species can appear in significant concentrations due to their long lifetimes.34,35 Hence, even with an excess of citrate, a normal condition in blood, the lifetime of Al(III) or Al(Cit) 1
1 complexes, the Al(Citr)–2,3-DPG ternary complexes could be formed. Finally, the results predict that Al–2,3-DPG species would only be formed in the absence of citrate. In addition, other factors such as non-equilibrium states and the slow ligand exchange rate of aluminum should be taken into account. Due to this slow rate, intermediate species can appear in significant concentrations due to their long lifetimes.34,35 Hence, even with an excess of citrate, a normal condition in blood, the lifetime of Al(III) or Al(Cit) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes could be long enough to form different complexes with 2,3-DPG.
1 complexes could be long enough to form different complexes with 2,3-DPG.
5 Conclusions
We have characterized the coordination mode and binding affinity for 26 complexes between aluminum and 2,3-DPG using density functional theory with the B3LYP functional. Our theoretical results support 2,3-DPG as an important chelator of aluminum in biological systems, especially in red cells, where 2,3-DPG is present in significant concentrations. We have also determined that there is a high variety of possible species with preference of coordination to 2-phosphate groups, and a competitive situation between acetate and 3-phosphate binding for the second chelator functional group. In the presence of citrate, we predict the formation of ternary compounds, even though at high concentrations of citrate the Al(Cit)2 species would be predominant. The complexes characterized in this work will be very valuable to interpret experimental information and identify possible deleterious Al–2,3-DPG complexes.Acknowledgements
Financial support comes from Eusko Jaurlaritza and the Spanish Office for Scientific Research. The SGI/IZO–SGIker UPV/EHU is gratefully acknowledged for the generous allocation of computational resources. XL would like to thank the Spanish Ministerio de Ciencia e Innovacion (CTQ2012-38496-C05-04) for funding.References
- C. Exley, J. Inorg. Biochem., 2003, 97, 1 CrossRef CAS.
- C. Exley, Trends Biochem. Sci., 2009, 34, 589 CrossRef CAS PubMed.
- T. L. Macdonald and R. B. Martin, Trends Biochem. Sci., 1988, 13, 15 CrossRef CAS.
- P. Vasudevaraju, M. Govindaraju, A. P. Palanisamy, K. Sambamurti and K. S. J. Rao, Indian J. Med. Res., 2008, 128, 545 CAS.
- L. Tomljenovic, J. Alzheimer’s Dis., 2011, 23, 567 CAS.
- T. Kiss, J. Inorg. Biochem., 2013, 128, 156 CrossRef CAS PubMed.
- J. I. Mujika, E. Rezabal, J. M. Mercero, F. Ruipérez, D. Costa, J. M. Ugalde and X. Lopez, Comput. Struct. Biotechnol. J., 2014, 9, e201403002 Search PubMed.
- M. Hémadi, G. Miquel, P. H. Kahn and J. M. El Hage Chahine, Biochemistry, 2003, 42, 3120 CrossRef PubMed.
- K. Atkári, T. Kiss, R. Bertani and R. B. Martin, Inorg. Chem., 1996, 35, 7089 CrossRef PubMed.
- T. Kiss, P. Zatta and B. Corain, Coord. Chem. Rev., 1996, 149, 329 CAS.
- D. Mazzuca, N. Russo, M. Toscano and A. Grand, J. Phys. Chem. B, 2006, 110, 8815 CrossRef CAS PubMed.
- J. R. Walton, Neurotoxicology, 2006, 27, 385 CrossRef CAS PubMed.
- V. B. Gupta, S. Anitha, M. L. Hegde, L. Zecca, R. M. Garruto, R. Ravid, S. K. Shankar, R. Stein, P. Shanmugavelu and K. S. J. Rao, Cell. Mol. Life Sci., 2005, 62, 143 CrossRef CAS PubMed.
- C. Exley, Coord. Chem. Rev., 2012, 256, 2142 CrossRef CAS PubMed.
- M. Abdel-ghany, A. Khalek and D. Shalloway, J. Biol. Chem., 1993, 268, 11976 CAS.
- R. B. Martin, Acc. Chem. Res., 1994, 27, 204 CrossRef CAS.
- M. Touam, F. Martinez, B. Lacour, R. Bourdon, J. Zingraff, S. Dicuilio and T. Drueke, Clin. Nephrol., 1983, 19, 295 CAS.
- K. Rosenlöf, F. Fyhrquist and R. Tenhunen, Lancet, 1990, 335, 247 CrossRef.
- J. L. Lin, M. T. Kou and M. L. Leu, Nephron, 1996, 74, 33 CrossRef CAS PubMed.
- M. Suwalsky, B. Ungerer, F. Villena, B. Norris, H. Cárdenas and P. Zatta, J. Inorg. Biochem., 1999, 75, 263 CrossRef CAS.
- M. Suwalsky, B. Ungerer, F. Villena, B. Norris, H. Cárdenas and P. Zatta, Brain Res. Bull., 2001, 55, 205 CrossRef CAS.
- M. Lubin, E. Bylaska and J. Weare, Chem. Phys. Lett., 2000, 322, 447 CrossRef CAS.
- A. J. Sillanpää, J. T. Päivärinta, M. J. Hotokka, J. B. Rosenholm and K. E. Laasonen, J. Phys. Chem. A, 2001, 105, 10111 CrossRef.
- A. J. A. Aquino, D. Tunega, G. Haberhauer, M. H. Gerzabek and H. Lischka, Phys. Chem. Chem. Phys., 2001, 3, 1979 RSC.
- T. Swaddle, Coord. Chem. Rev., 2001, 219, 665 CrossRef.
- E. Rezabal, J. M. Mercero, X. Lopez and J. M. Ugalde, J. Inorg. Biochem., 2006, 100, 374 CrossRef CAS PubMed.
- E. Rezabal, J. M. Mercero, X. Lopez and J. M. Ugalde, ChemPhysChem, 2007, 8, 2119 CrossRef CAS PubMed.
- E. Rezabal, J. M. Mercero, X. Lopez and J. M. Ugalde, J. Inorg. Biochem., 2007, 101, 1192 CrossRef CAS PubMed.
- A. L. Oliveira de Noronha, L. Guimarães and H. A. Duarte, J. Chem. Theory Comput., 2007, 3, 930 CrossRef CAS.
- M. B. Hay and S. C. B. Myneni, J. Phys. Chem. A, 2008, 112, 10595 CrossRef CAS PubMed.
- X. Yang, Q. Zhang, L. Li and R. Shen, J. Inorg. Biochem., 2007, 101, 1242 CrossRef CAS PubMed.
- J. F. Fan, L. J. He, J. Liu and M. Tang, J. Mol. Model., 2010, 16, 1639 CrossRef CAS PubMed.
- B. M. Lu, X. Y. Jin, J. Tang and S. P. Bi, J. Mol. Struct., 2010, 982, 9 CrossRef CAS PubMed.
- J. Beardmore, G. Rugg and C. Exley, J. Inorg. Biochem., 2007, 101, 1187 CrossRef CAS PubMed.
- J. Beardmore and C. Exley, J. Inorg. Biochem., 2009, 103, 205 CrossRef CAS PubMed.
- N. B. Luque, J. I. Mujika, E. Rezabal, J. M. Ugalde and X. Lopez, Phys. Chem. Chem. Phys., 2014, 16, 20107 RSC.
- I. Sóvágó, T. Kiss and R. B. Martin, Polyhedron, 1990, 9, 189 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision A.1, Gaussian Inc, Wallingford CT, 2009 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 2999 CrossRef CAS PubMed.
- J. Alí-Torres, L. Rodríguez-Santiago and M. Sodupe, Phys. Chem. Chem. Phys., 2011, 13, 7852 RSC.
- R. M. C. Dawson and W. Elliott, Data for Biochemical Research, Oxford science publications, Clarendon Press, 1989 Search PubMed.
- J. I. Mujika, J. M. Ugalde and X. Lopez, Phys. Chem. Chem. Phys., 2012, 14, 12465 RSC.
- J. I. Mujika, J. M. Ugalde and X. Lopez, J. Phys. Chem. B, 2014, 18, 1345 Search PubMed.
- A. Lakatos and F. Evanics, Eur. J. Inorg. Chem., 2001, 3079 CrossRef CAS.
- X. Ma, L. Li, C. Xu, H. Wei, X. Wang and X. Yang, Molecules, 2012, 17, 9379 CrossRef CAS PubMed.
- S. Murko, R. Milacic and J. Scancar, J. Inorg. Biochem., 2007, 101, 1234 CrossRef CAS PubMed.
- J. I. Mujika, X. Lopez, E. Rezabal, R. Castillo, S. Marti, V. Moliner and J. M. Ugalde, J. Inorg. Biochem., 2011, 105, 1446 CrossRef CAS PubMed.
- J. I. Mujika, B. Escribano, E. Akhmatskaya, J. M. Ugalde and X. Lopez, Biochemistry, 2012, 51, 7017 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra06796k |
| This journal is © The Royal Society of Chemistry 2015 |