Structural evolution of a Si melt in nanoscale confined space
Leining Zhanga,
Weikang Wua,
Hongru Rena,
Jichen Dongb,
Yao Liu*a and
Hui Li*a
aKey Laboratory for Liquid-Solid Structural Evolution and Processing of Materials, Ministry of Education, Shandong University, Jinan 250061, People's Republic of China. E-mail: liuyao@sdu.edu.cn; lihuilmy@hotmail.com
bDepartment of Mechanical and Biomedical Engineering, City University of Hong Kong, 83 Tat Chee Avenue, Hong Kong
First published on 26th May 2015
Abstract
Molecular dynamics (MD) simulations are performed to systematically study the structural evolution of a Si melt confined in nanoscale space. The freezing Si structure at 300 K is stratification which is composed of a stable crystalline shell and a metastable glassy core. Due to the spatial restriction effect, the confined structure consists of higher-coordinated clusters compared to the bulk Si. It is revealed that the statistical average of the ordered shell and the disordered core gives rise to the split of the second peak of the pair distribution function curves of the Si melt. Moreover, increasing the cavity size is detrimental to the stability of the layered configuration of the confined melt and increasing the cooling rate mainly influences the arrangement of Si atoms adjacent to the SWCNT wall. Interestingly, we also find that the cylindric cavity is more beneficial than the square one in inducing the formation of long-range crystalline order in nanoscale space.
1. Introduction
Polymorphic Si, including monocrystalline, polycrystalline, amorphous and other allotropes has been widely used in various electronic devices as one of the most important functional materials during the last few decades.1–4 It is known that the atomic structure of the material determines its final performance. Previous studies show that bulk Si in the solid state is a semiconductor, while it is metallic in the liquid state.5,6 However, low-dimensional Si nanostructures are considered to possess distinctive structures and properties that are remarkably different from those of bulk counterparts.7–12 In fact, Si nanowires (Si NWs) have aroused significant attention in recent years because of their intriguing structural, surface, electronic, and mechanical properties and potential applications in future nanoscale devices.13–16 Menon et al.17 demonstrated that cage-like Si NWs are able to maintain their structural integrity over a larger range of strain conditions than the tetrahedral Si NWs. Rurali et al.18 have addressed that there is an intrinsic relation between the reconstruction of Si NW facets and its transport properties, which makes the use of Si NWs as conductors without doping possible.The use of nanopores as templates is a powerful way of synthesizing nano-materials in a controlled manner. In particular, exploring the possibility of using single-walled carbon nanotubes (SWCNTs) as nano-moulds to synthesize one-dimensional nano-materials has aroused increasing interest.19–24 It has been well acknowledged that SWCNTs exhibit exceedingly high mechanical, thermal and chemical stability and well-defined cavity.25–27 A wide array of materials, such as metals or their compounds, liquids, and even fullerenes, have been found, both theoretically and experimentally, to form intriguing one-dimensional structures within SWCNTs.28–34 Compared to weakly bonded molecules and non-directionally bonded metals, the covalently bonded Si might exhibit different structural evolution behaviors when encapsulated in SWCNTs, which can be used to obtain Si NWs with peculiar structures and properties. It has been demonstrated that Si NWs is an attractive anode material for Li ion batteries with low discharge potential and high charge capacity, but Si anodes have limited applications because their volume changes significantly during charging and discharging process, which results in pulverization and capacity fading.35,36 Here, using CNTs for encapsulating Si atoms also offers an effective way to minimize the volume expansion and resist oxidation, which may result in a promising nano-composite for the anode of Li ion battery. However, a comprehensive physical and dynamic insight into the structural evolution of Si melt confined in SWCNTs during freezing has not been achieved until now.
In this study, the detailed structural transformation from liquid to solid of Si melt confined in SWCNTs is systematically explored through MD simulations, which have been extensively proved to be a powerful and reliable tool to study the structural evolution of nano-materials at the atomic scale. The results would offer an opportunity to well understand the structural evolution of liquid Si in nanoscale cavity and may provide a possible way to fabricate novel Si NWs structures.
2. Models and theoretical methods
All MD simulations are carried out by using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) package.37 To simulate the freezing process, NPT ensemble with the Nosé–Hoover thermostat and barostat is chosen to control the temperature and pressure. The pressure is maintained at 1 bar. The Velocity-Verlet algorithm is used with an integration time step of 1.0 fs. The Stillinger–Weber (SW) potential and the adaptive intermolecular reactive empirical bond order (AIREBO) potential are employed to describe the Si–Si interaction38 and the C–C interaction,39 respectively. The C–Si interaction40 is described by Tersoff potential, which has been successfully used to simulate the Si–CNT systems.41–43 The initial configurations are constructed by filling the SWCNTs with a small amount of Si melt step by step until the SWCNTs are fully loaded. At each step the structures are relaxed at 3000 K for 20 ps. All the SWCNTs are 49.19 Å in length. The density of the Si melt in different SWCNTs for these configurations is almost the same and is 2.10 g cm−3. With the increase of the SWCNT diameter, these structures consist of 50 to 1280 Si atoms and 320 to 1600 C atoms. These configurations are then quenched from 3000 to 300 K with cooling rates ranging from 0.1 to 10 K ps−1. Such models are reasonable because previous studies have demonstrated that SWCNTs encapsulating Si nano-particles are stable under high temperature.41 In addition, the freezing process of bulk Si without any restriction is also calculated as a comparison.3. Results and discussion
Si melt is first encapsulated in a SWCNT(12, 12) to explore its freezing behavior with a cooling rate of 1 K ps−1. Fig. 1(a)–(d) reveal the configurations of Si in this SWCNT during cooling from 3000 to 300 K. The Si melt initially has a blurring outmost layer and a completely disordered core. After the encapsulation, the Si atoms adjacent to the tube wall tend to be arranged in order. When the temperature keeps decreasing, the Si melt in the outmost layer gets increasingly ordered and a neighboring second layer appears between the outmost layer and core. But, the second layer is much more disordered than the outmost one and no more new layer emerges. Moreover, the outlayer Si atoms are completely ordered at 300 K, and their arrangement is similar to the (1 0 0) face of Si crystal. The stratification phenomenon has been found widely in other confined melt, which is caused by the short-range interaction between interfaces.44 It can be seen that the confined Si atoms can be obviously divided into two parts by calculating the average potential energy per atom at 300 K, one is the outmost layer next to the SWCNT wall (SiW) and the other is the internal part (SiI), as shown in Fig. 1(e). The result shows that ESiW = −7.515 eV and ESiI = −3.997 eV, indicating the fact that the completely ordered outlayer SiW is more stable than the disordered SiI structure. This is because the Si atoms in the outmost layer arrange orderly firstly in their lowest energy with the strong Si–SWCNT interfacial interaction, and then act as a new wall to restrict the inner Si atoms, which forms second disordered layered structure with bits of pentagonal and hexagonal structures paralleled to the wall. The second layer is relatively disordered with many defects because those Si atoms link together through directional covalent bonds, thus it is difficult to meet the direction requirement of bond angle of the Si crystal during the freezing process, indicating that the arrangement of the second layer results from the combined action of the Si–Si interfacial interaction and the Si–Si lattice energy. Because the second layer with higher energy is metastable and cannot act as the restricting wall, the arrangement of the atoms is disordered even the circles are not parallel to the wall any more, indicating that only the stable wall is beneficial to form the layered structure. To further explore the structural transformation, Fig. 2 shows the average coordination number of different parts. Clearly, the coordination number shows a strong dependence on temperature. For SiI, its average coordination number is almost the same as that of bulk Si at high temperature, but at low temperature, the case is different. When quenched to 300 K the coordination number of bulk Si follows N4 (0.546) > N5 (0.406) > N6 (0.044) > N7 (0.002) (here, N4–7 represents the percentage of 4–7 fold coordinated clusters), in consistent with previous study45 showing that four-fold coordination predominates in amorphous silicon at room temperature, followed by five-fold coordinated clusters. In addition, the coordination number fraction of SiW follows N5 (0.760) > N4 (0.150) > N6 (0.009) at 300 K. The outlayer Si atoms connect with the internal atoms by covalent bounds owing to the limited space, making the melt produce much five-fold coordination clusters. The coordination numbers of SiI at 300 K follows N5 (0.439) > N4 (0.349) > N6 (0.177) > N7 (0.023). Interestingly, N5 of SiI is larger than that of bulk Si but lower than that of SiW. The solidified structure confined in SWCNT possesses higher coordination number compared to the bulk Si because of the spatial restriction effect. In addition, the average coordination number of SiI is larger than that of SiW in the whole freezing process, which makes whole structure have a low-coordinated shell but a high-coordinated core. This fact indicates that the SWCNT wall limits the formation of high-coordinated Si clusters near the wall in the vertical direction.The freezing behavior of Si melt in SWCNTs can be influenced by many factors, such as diameter of the SWCNT, cooling rate and geometry of the cavity etc., which may play important roles in controlling the configuration of the solidified structure. To reveal the influence of diameter on the freezing behavior of Si melt, armchair SWCNTs with different diameters indexed by (4, 4), (6, 6), (8, 8), (10, 10), (12, 12), (14, 14), (16, 16), (18, 18) and (20, 20) are chosen as the moulds. Fig. 3(a) shows the snapshots of the Si melt quenched to 300 K with a cooling rate of 1 K ps−1. It is obvious that all the confined Si structures possess a coaxial cylindrical layer near the wall. As the diameter increases, the outmost and second layers exist stably all the time, while the third layer with lower density emerges only in SWCNT(14, 14). Interestingly, when further increasing the diameter, a completely disordered core structure appears instead of the third layer. With the increase of the diameter, the Si–SWCNT interfacial interaction decays and the effect of the Si–Si lattice energy gradually emerges, the Si–Si energy becomes predominate and makes the atoms in the core form a disordered structure. It is worth noting that, in large diameter SWCNTs, amounts of vacancies appear in the core of the Si solid compared with the outmost and second layers because of the volume contraction of the core during the freezing. The strong interfacial interactions make the Si atoms of the outmost and second layers tend to be preferentially fixed near the wall, but the Si atoms in the core are more free than the atoms of outmost layer to easily allow a volume contraction induced by the Si–Si lattice energy. To identify the layered structure more clearly, the radial density profiles are shown in Fig. 3(b). The result shows that the position of the first peak of the radial density is unchanged all the time, suggesting that the distance between the outermost Si layer and the tube wall is constant because of the strong Si–SWCNT interfacial interaction. The second peak shifts toward larger distances until the diameter increases to 13.56 Å (SWCNT(10, 10)), which results from the strong spatial restriction effect of small diameter. Because the atoms of the second layer are controlled by the combined action of the Si–Si interfacial interaction and the Si–Si lattice energy, it forms a disordered layer which makes the height of the second peak slightly be suppressed.
In order to further understand the structural transformation of Si melt, the pair distribution function (PDF) curves, g(r), of the Si melt at different stages are shown in Fig. 4. Fig. 4(a) shows that, when the diameter of the SWCNT is small, the first peak shifts to large distances and the intensity increases with the increase of the diameter because of the strong restriction on the Si melt. When the diameter of the cavity increases, the confinement of the wall on Si atoms is weakened which makes the distance between the atoms increase. When the diameter of the SWCNT exceeds 13.56 Å (SWCNT(10, 10)), the restriction of the wall does not play the dominant role any more, making the position of the first peak be recovered to its normal state. By comparing Fig. 4(b) and (c), it can be found that the overall g(r) curves of the confined melt are similar to those of SiW in SWCNT(10, 10), SWCNT(12, 12) and SWCNT(14, 14), because the number of SiW atoms is much more than that of SiI atoms in these three models (the proportion of SiW atoms accounted for total Si atoms is 74.52%, 61.80% and 52.75%, respectively). As can be seen from Fig. 4(c), the second peak moves to larger distance with the increase of diameter. In terms of the physical significance of PDFs,46 the abscissa value Ri of the ith peak always represents the average distance from ith nearest-neighbor shell to the central atom, for example, R1 represents the average distance of the first nearest-neighbor shell. Since the distance between the nearest-neighbor atoms remains unchanged, with the reduction of the curvature of the cylindrical shell, the distance from the second nearest-neighbor atoms to the central atom would increase, leading the second peak to move to larger distances. In Table 1, the distance from the second nearest-neighbor atoms to the central atom is calculated through their specific geometrical relation. As shown in the sketch map in Table 1, the distance can be computed as follows:
| DSi = DCNT − 1.627 × 2 | (1) |
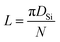 | (2) |
 | (3) |
Fig. 4(d) shows that the PDF curves of the SiI and the bulk Si are similar because the Si–Si lattice energy is predominate in the internal region and the constriction effect is weakened. A pronounced bump appears between the first and second peaks, which is a characteristic of glassy structures.47 The formation of the bump is directly related to the arrangement of neighboring atoms, suggesting the existence of the short-range order in the melt. This is due to the fact that the arrangement of atoms in the freezing structure does not satisfy the directional requirement of Si–Si covalent bonds, leading to the lack of long-range ordered structures. Moreover, all peaks intensity of the SiI reduces greatly compared with the bulk one, suggesting that the order degree of the internal Si melt declines owing to the spatial restriction effect. Importantly, we can observe the split of the second peak of g(r) curves for Si confined in SWCNT(12, 12) and SWCNT(14, 14). As verified in Fig. 4(d), the PDF of the outmost layer shows typical crystal feature, and that of the internal layer indicates glassy characteristic, but the statistical average of the outmost crystal structure and the internal core glassy structure exhibits split feature, thus we conclude that the split of the second peak is the result of the combined effect of the SiW and the SiI. It should be noted that the R1 of Si melt at different states under 300 K follows SiW (r = 2.65 Å) > SiI (r = 2.45 Å) > bulk Si (r = 2.35 Å). When further increasing the diameter, the g(r) curves of SiW present different characteristics, because the reduction of the curvature makes the structure of SiW be like the Si crystal. If we increase the number of the internal Si atoms, the split second peak would turn into two independent peaks like the crystal peak.
To reveal the effect of cooling rate on the freezing behavior, the PDF curves of Si melt in SWCNT(18, 18) quenched to 300 K with different cooling rates are calculated and shown in Fig. 5(a). As the cooling rate increases, the intensity of the first peak has almost no change, while others are significantly suppressed, manifesting that the structure of the confined Si melt becomes more disordered and freezes into a low ordering degree structure at high cooling rate. Fig. 5(b) and (c) show the PDF curves of SiW and SiI, respectively. The peaks of SiW PDF curve obviously become shorter and wider with the increase of cooling rate, and some peaks (such as the second, third and fourth peaks) even disappear when the cooling rate increases to 10 K ps−1. In contrast, the PDF curves of SiI have no noticeable changes. These phenomena suggest that the change of cooling rate mainly influences the arrangement of Si atoms adjacent to the SWCNT wall.
To demonstrate the confinement effect of geometry on the melt, the cylindric cavity is changed to the square one. Fig. 6(a) shows the configurations of Si melt quenched to 300 K with a cooling rate of 1 K ps−1 confined in square cavity with different sizes, as denoted by SiS1, SiS2 and SiS3 for simplicity, respectively. Similar to the cases of cylindric SWCNTs, there is an obvious stratification between Si atoms adjacent to tube wall and the internal ones, and the internal structure becomes more and more disordered with the increase of the tube size. It can be seen that, the Si atoms arrange more orderly with lower potential energy at the corner, which is induced by the relatively strong interaction between the Si atoms and the cavity wall with a large curvature. We also calculate the PDF of quenched bulk Si melt and Si melt encapsulated in square-shaped cavities with different sizes. Fig. 6(b(I)) shows that the order degree reduces with the increase of cavity size, which is consistent with the configurations in Fig. 6(a). Fig. 6(b(II)) illustrates the effect of cavity shape on the PDF curve of Si melt. The first peak of Si melts confined in square and cylindric cavity shifts to larger distances compared to the bulk one. More importantly, when the cross-sectional areas are same, the order degree of quenched Si melt confined in cylindric cavity is higher than that in square cavity, indicating that the cylindric cavity is superior to the square one in forming long-range order which can be demonstrated by the crystalline peak appeared in the PDF curve of the melt in SWCNT.
4. Conclusion
This study systematically investigated the structural evolution of a Si melt confined in nanoscale cavity. Owing to the competition between the interfacial interaction and the Si–Si interaction, a coaxial layered structure composed of an ordered shell and an internal disordered core forms in the one-dimensional space during the rapid cooling process. The split of the second peaks of the PDF curves is observed, which is a result of the combined effect of the ordered shell and the disordered core. During the structural evolution process, Si melt tends to form more five-coordinated clusters owing to the spatial restriction. Cylindric cavity is found to be more helpful than the square one to form long-range crystalline order because of its different curvature.This work may spark off new ways to explore and control the structural evolution of confined Si melt in order to provide theoretical guidance in fabricating nano-material in confined cavity.
Acknowledgements
The authors would like to acknowledge the support from the National Natural Science Foundation of China (Grant no. 51271100) and (Grant no. 51402170). This work is also supported by the National Basic Research Program of China (Grant no. 2012CB825702). This work is also supported by the Special Funding in the Project of the Taishan Scholar Construction Engineering.References
- X. Liu, J. Feldman, D. Cahill, R. Crandall, N. Bernstein, D. Photiadis, M. Mehl and D. Papaconstantopoulos, Phys. Rev. Lett., 2009, 102, 035901 CrossRef PubMed
.
- R. J. Knuesel and H. O. Jacobs, Adv. Mater., 2011, 23, 2727–2733 CrossRef CAS PubMed
.
- S. W. Chang, V. P. Chuang, S. T. Boles and C. V. Thompson, Adv. Funct. Mater., 2010, 20, 4364–4370 CrossRef CAS
.
- F. Kail, J. Farjas, P. Roura, C. Secouard, O. Nos, J. Bertomeu and P. R. i. Cabarrocas, Phys. Status Solidi RRL, 2011, 5, 361–363 CrossRef CAS
.
- N. I. Jakse, L. Hennet, D. L. Price, S. Krishnan, T. Key, E. Artacho, B. Glorieux, A. Pasturel and M.-L. Saboungi, Appl. Phys. Lett., 2003, 83, 4734 CrossRef CAS
.
- W. Jank and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 1497 CrossRef CAS
.
- Y. Zhao and B. I. Yakobson, Phys. Rev. Lett., 2003, 91, 035501 CrossRef PubMed
.
- Y. Wang, B. Li and G. Xie, RSC Adv., 2013, 3, 26074 RSC
.
- P. De Padova, C. Quaresima, C. Ottaviani, P. M. Sheverdyaeva, P. Moras, C. Carbone, D. Topwal, B. Olivieri, A. Kara, H. Oughaddou, B. Aufray and G. Le Lay, Appl. Phys. Lett., 2010, 96, 261905 CrossRef
.
- G. G. Guzman-Verri and L. C. Lew Yan Voon, J. Phys.: Condens. Matter, 2011, 23, 145502 CrossRef CAS PubMed
.
- Y. He, X. Li, H. Li, Y. Jiang and X. Bian, Nanoscale, 2014, 6, 4217–4224 RSC
.
- J. Bai, H. Tanaka and X. C. Zeng, Nano Res., 2010, 3, 694–700 CrossRef CAS
.
- K. Nishio, T. Ozaki, T. Morishita, W. Shinoda and M. Mikami, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 075431 CrossRef
.
- M. Menon and E. Richter, Phys. Rev. Lett., 1999, 83, 792–795 CrossRef CAS
.
- R. Kagimura, R. W. Nunes and H. Chacham, Phys. Rev. Lett., 2005, 95, 115502 CrossRef CAS PubMed
.
- K. Nishio, T. Morishita, W. Shinoda and M. Mikami, J. Chem. Phys., 2006, 125, 074712 CrossRef PubMed
.
- M. Menon, D. Srivastava, I. Ponomareva and L. A. Chernozatonskii, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 125313 CrossRef
.
- R. Rurali and N. Lorente, Phys. Rev. Lett., 2005, 94, 115502 CrossRef
.
- Y. Jiang, H. Li, Y. Li, H. Yu, K. M. Liew, Y. He and X. Liu, ACS Nano, 2011, 5, 2126–2133 CrossRef CAS PubMed
.
- H. Gao, Y. Kong, D. Cui and C. S. Ozkan, Nano Lett., 2003, 3, 471–473 CrossRef CAS
.
- C.-c. Ling, Q.-z. Xue, D. Xia, M.-x. Shan and Z.-d. Han, RSC Adv., 2014, 4, 1107–1115 RSC
.
- J. W. Kang and H. J. Hwang, Nanotechnology, 2004, 15, 115–119 CrossRef CAS
.
- Y. Y. Jiang, H. Li, K. Zhang, H. Q. Yu, Y. Z. He and X. G. Song, Europhys. Lett., 2012, 97, 16002 CrossRef
.
- K. Koga, G. T. Gao, H. Tanaka and X. C. Zeng, Nature, 2001, 412, 802–805 CrossRef CAS PubMed
.
- P. G. Collins and P. Avouris, Sci. Am., 2000, 283, 62–69 CrossRef CAS PubMed
.
- Q. Zheng, Q. Xue, K. Yan, L. Hao, Q. Li and X. Gao, J. Phys. Chem. C, 2007, 111, 4628–4635 CAS
.
- K. Liew, C. Wong, X. He and M. Tan, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 075424 CrossRef
.
- W. Choi, J. Kang and H. Hwang, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 193405 CrossRef
.
- C. Guerret-Piecourt, Y. L. Bouar, A. Lolseau and H. Pascard, Nature, 1994, 372, 761–765 CrossRef CAS
.
- J. Won Kang and H. Jung Hwang, J. Phys. Soc. Jpn., 2004, 73, 738–744 CrossRef
.
- S. Arcidiacono, J. Walther, D. Poulikakos, D. Passerone and P. Koumoutsakos, Phys. Rev. Lett., 2005, 94, 105502 CrossRef CAS PubMed
.
- R. R. Fang, Y. Z. He, K. Zhang and H. Li, J. Phys. Chem. C, 2014, 118, 7622–7629 CAS
.
- Y. Maniwa, H. Kataura, M. Abe, S. Suzuki, Y. Achiba, H. Kira and K. Matsuda, J. Phys. Soc. Jpn., 2002, 71, 2863–2866 CrossRef CAS
.
- S. Okada, S. Saito and A. Oshiyama, Phys. Rev. Lett., 2001, 86, 3835 CrossRef CAS PubMed
.
- U. Kasavajjula, C. Wang and A. J. Appleby, J. Power Sources, 2007, 163, 1003–1039 CrossRef CAS
.
- C. K. Chan, H. Peng, G. Liu, K. McIlwrath, X. F. Zhang, R. A. Huggins and Y. Cui, Nat. Nanotechnol., 2008, 3, 31–35 CrossRef CAS PubMed
.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS
.
- F. H. Stillinger and T. A. Weber, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 5262–5271 CrossRef CAS
.
- S. J. Stuart, A. B. Tutein and J. A. Harrison, J. Chem. Phys., 2000, 112, 6472–6486 CrossRef CAS
.
- J. Tersoff, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 5566–5568 CrossRef
.
- K. Nishio, T. Ozaki, T. Morishita and M. Mikami, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 201401 CrossRef
.
- J. Diao, D. Srivastava and M. Menon, J. Chem. Phys., 2008, 128, 164708 CrossRef PubMed
.
- X. Zhang, M. Hu and D. Poulikakos, Nano Lett., 2012, 12, 3410–3416 CrossRef CAS PubMed
.
- J. N. Israelachvili, Intermolecular and Surface Forces, Academic Press, 1992 Search PubMed
.
- W. D. Luedtke and U. Landman, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 1164–1174 CrossRef CAS
.
- X. J. Liu, Y. Xu, X. Hui, Z. P. Lu, F. Li, G. L. Chen, J. Lu and C. T. Liu, Phys. Rev. Lett., 2010, 105, 155501 CrossRef CAS PubMed
.
- W. Luedtke and U. Landman, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 4656–4663 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2015 |







