Intermolecular OHN hydrogen bond with a proton moving in 3-methylpyridinium 2,6-dichloro-4-nitrophenolate†
Abstract
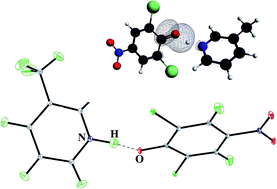
The neutron structure of 3-methylpyridinium 2,6-dichloro-4-nitrophenolate measured at different temperatures is used to discuss the structural parameters of the OHN intermolecular hydrogen bridges with the proton moving. The experimental and optimized structures, with the precise location of the proton, are used to explain the mechanism of proton transfer in the OHN hydrogen bridge.

 Please wait while we load your content...
Please wait while we load your content...