Vacancy mediated ionic conduction in Dy substituted nanoceria: a structure–property correlation study

Abstract

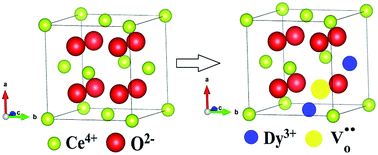
The oxygen vacancy evolution and ion dynamics in Dy doped nanoceria have been investigated with microstructural, optical and ionic conductivity studies. The influence of Dy³⁺ ions on the microstructures and the optical and ionic conductivity properties of these nanoparticles has been studied using X-ray diffraction, HR-TEM, EDAX, UV-vis, Raman and impedance spectroscopy. From Rietveld refinement of the XRD profiles, it has been found that the oxygen vacancies, lattice parameters and Ce–O bond lengths increase with Dy³⁺ ion concentration. The Rietveld analysis, together with HR-TEM, confirms the cubic fluorite structure with space group Fm3̄m of all the samples. The EDAX spectra show good stoichiometry of the different atoms in the samples. The direct band gap, calculated from UV-vis spectra, shows a red shift with increasing concentration of Dy³⁺ ions. Raman spectroscopy studies of the samples gave insight into their vibrational properties and pointed to the fact that the oxygen vacancy content increased significantly with the doping concentration. The number of oxygen vacancies and their interaction with dopant cations strongly influence the electrical properties of Dy doped ceria.

---

1. Introduction

The ionic conductivity of ceria based solid solutions has been reported to be an order of magnitude greater than that of yttrium-stabilized zirconia (YSZ) when it is in nanocrystalline form.¹ Ceria based nanomaterials have also found applications as catalytic supports in automotive exhaust systems.² Rare earth elements are praised as valuable materials due to their special optical, electrical and magnetic properties, which are attributed to their particular electron configurations.³ When ceria is doped with rare earth elements, the substitution of Ce⁴⁺ in ceria by these trivalent cations distorts the lattice structure and generates oxygen vacancies,⁴ which permits high oxygen ion conduction. The oxygen vacancy concentration of CeO₂ can be varied by varying the dopant concentration.⁵ Rare earth doped ceria is also a good candidate as a wavelength converter of near UV photons to IR photons.⁶ A comprehensive knowledge of the crystal structures of these compounds and a better understanding of their mechanism of ionic conduction are therefore required to develop better electrolyte materials. Hence, in order to use rare earth doped ceria as electrolyte materials, many researchers have studied the crystal structures, ordering of oxygen vacancies and diffusion paths of these ionic conductors.^7–10 The movements of these oxygen vacancies are influenced by their interactions with dopant cations. A relatively small concentration of point defects may affect the physical properties of these materials in very significant ways.¹¹ Raman spectroscopy is an essential tool to investigate this type of local structural distortion.¹² The main difficulty for the application of rare earth doped ceria in SOFC electrolytes is the creation of both electronic and ionic charge carriers at low oxygen partial pressures. The ionic conduction in rare earth doped ceria is dominated by the association between the trivalent cations and the oxygen vacancies. Among the various rare earth doped ceria materials, ceria doped with Sm³⁺ and Gd³⁺ shows higher ionic conductivity because of the optimal radii of these elements and, therefore, their smaller association enthalpy.^13,14 Recent studies¹⁵ have also pointed out that Dy doped ceria may be a promising solid electrolyte material for applications in low temperature SOFCs.

In our present work, Dy doped Ce_1−xDy_xO_2−δ (0.0 ≤ x ≤ 0.5) nanoparticles were prepared using the citrate auto-ignition method. The detailed microstructures and the optical properties of these nanoparticles were investigated. The effect of dysprosium doping on the evolution of oxygen vacancies with respect to microstructure and optical properties, and the dependence of electrical conductivity on the doping concentration and oxygen vacancies, are discussed and correlated.

2. Materials and methods

The Dy doped ceria nanomaterials Ce_1−xDy_xO_2−δ (0.0 ≤ x ≤ 0.5) were prepared by using a low temperature citrate auto-ignition method. Ce(NO₃)₃·6H₂O (99.9%) and Dy₂O₃ (99.9%) were used as starting materials. The process of sample preparation has been described in our previous work.¹⁶ The as prepared powdered samples were annealed at 400 °C for 2 h, then sintered at 600 °C for 6 h. During annealing/sintering the temperature was increased at the rate of 5 °C min⁻¹, and the materials were then cooled to room temperature by normal furnace cooling. To identify the crystal structures and phase purity of the samples, X-ray diffraction profiles were recorded with a powder X-ray diffractometer (BRUKER, Model D8 Advance-AXS) using CuK_α radiation [ λ = 1.5406 Å] from 2θ = 20° to 90° with a step size of 0.05°. The microstructural analyses at high magnification were performed by placing the particles in a Formvar-carbon coated 300 mesh copper grid with the help of a transmission electron microscope (JEOL, Model JEM-2010) operated at 200 kV. The TEM micrographs were further analyzed using the Gatan microscopy suite. The compositions of the samples were evaluated by energy dispersive X-ray analysis (Hitachi S-3500). Ultraviolet-visible (UV-vis) absorption spectra were taken at room temperature in the wavelength range of 200–1100 nm using a Shimadzu spectrophotometer (Model-1800). Raman spectra of the materials were recorded at room temperature using a Triple Raman Spectrometer (Jobin-Yvon Horiba T64000) equipped with a TE cooled charge coupled-device detector and an Olympus microscope using a He–Ne laser at the 632.817 nm line as the excitation source in the wavenumber range of 200–800 cm⁻¹. For the electrical measurements, cylindrical pellets were prepared from sintered powder by uniaxial pressing in a 10 mm diameter stainless steel die. The pellets were covered on both sides with conductive graphite paste to make the electrodes. The electrical measurements were performed using two probe methods in air. A LCR meter (HIOKI, Model 3532-50) interfaced with a PC was used to collect the electrical data in the frequency range of 42 Hz–5 MHz and in the temperature range of 250–550 °C.

3. Results and discussion

3.1. X-Ray diffraction analysis and Rietveld refinement

Fig. 1(a) shows the XRD pattern of the Ce_1−xDy_xO_2−δ (x = 0.00–0.50) samples. It may be found that when ceria is doped with Dy, there is no noticeable change in the diffraction pattern, i.e. any additional peak due to Dy is absent. This confirms the complete dissolution of Dy into the ceria lattice. The observed peaks in the XRD pattern were well indexed and consistent with the reference data [JCPDS file: 34-03940]. The observed Bragg reflection peaks confirmed the cubic fluorite structure of the samples. We have plotted the maximum intensity peak (111) against the concentration of Dy in Fig. 1(b). It can be seen from Fig. 1(b) that the peak shifts towards the lower angle side with increasing doping concentration (x). This shift of the (111) peak clearly indicates the lattice expansion with Dy content in the ceria lattice.

Fig. 1 (a) XRD patterns of the doped and undoped ceria Ce_1−xDy_xO_2−δ (x = 0.00–0.50). (b) Shift of (111) peak shift with doping concentration x. The refined XRD patterns obtained from Rietveld analysis of the samples for (c) x = 0.20 and (d) x = 0.50.

To obtain microstructural information for the samples, we have performed Rietveld analysis of the XRD data using MAUD 2.33 software, which is specially designed to simultaneously refine both the structural and microstructural parameters through a least squares method. Fig. 1(c) and (d) show the refined XRD pattern obtained from Rietveld analysis for the samples x = 0.20 and x = 0.50 respectively. The shape of the diffraction profile is fitted with a pseudo-Voigt function (described by Gaussian + Lorentzian functions with a refinable degree of mixing) with asymmetry because this function takes individual results into account for both the particle size and strain broadening of the experimental data.¹⁷ The angular dependence of the peak full width at half maximum (FWHM) is described by Caglioti's formula. The background of each XRD profile is fitted using a polynomial of degree 5. The difference between the observed and simulated diffraction patterns was minimized using the Marguardt least-squares procedure. This minimization was carried out using reliability index parameters such as weighted residual error (R_wp), expected error (R_exp) and goodness of fit (GoF).^18–20 These parameters are defined as:

where Y_o,n and Y_c,n are the observed and calculated data at point n, respectively; Bkg_n is the background at data point n; N is the number of data points; P is the number of parameters; and w_n is the weighting factor given to data point n. In counting statistics, this last factor is given by w_n = 1/σ(Y_o,n)², where σ(Y_o,n) is the error in Y_o,n. Both R_wp and GoF are good global indicators of the refinement process, since the numerators of these factors contain the residual function which is being minimized. A desirably good refinement is represented by the low values of these parameters: R_wp around 0.10 for XRD in a conventional diffractometer, and GoF around 1.²¹ In all refinements, GoF is between 1.1 and 1.2, which indicates the success of the refinement. Different Reitveld parameters, such as R_exp, R_wp and GoF, for each XRD profile are listed in Table 1. We have evaluated the effective particle size (D) and RMS strain (〈ε²〉^1/2) using the Popa model.²² Other structural parameters such as lattice parameter, Ce–O bond length, atomic position and occupancies were calculated and are given in Table 1.

Table 1 Rietveld refinement analysis results and theoretical densities for the Ce_1−xDy_xO_2−δ samples (x = 0.00–0.50). The errors after the fourth decimal are indicated inside parentheses

Ce1−xDyxO2−δ (x = 0–0.5)	x = 0.00	x = 0.10	x = 0.15	x = 0.20	x = 0.25	x = 0.30	x = 0.40	x = 0.50
Crystal system	Cubic	Cubic	Cubic	Cubic	Cubic	Cubic	Cubic	Cubic
Space group	Fm3̄m	Fm3̄m	Fm3̄m	Fm3̄m	Fm3̄m	Fm3̄m	Fm3̄m	Fm3̄m
Atomic co-ordinate
Ce(4a)
(x,y,z)	(0,0,0)	(0,0,0)	(0,0,0)	(0,0,0)	(0,0,0)	(0,0,0)	(0,0,0)	(0,0,0)
Occupancy	0.9989(7)	0.9106(1)	0.8499(5)	0.8039(3)	0.7632(2)	0.7155(1)	0.6265(7)	0.5091(3)
Dy(4a)
(x,y,z)	—	(0,0,0)	(0,0,0)	(0,0,0)	(0,0,0)	(0,0,0)	(0,0,0)	(0,0,0)
Occupancy	—	0.0894(5)	0.1501(3)	0.1961(8)	0.2368(4)	0.2845(4)	0.3735(7)	0.4909(2)
O(8c)
(x,y,z)
Occupancy	0.9859(1)	0.9482(5)	0.9334(8)	0.8898(6)	0.8813(2)	0.8634(1)	0.8176(1)	0.7698(5)
Lattice parameter (Å)	5.3976(9)	5.4019(1)	5.4045(5)	5.4064(4)	4.4085(3)	5.4101(1)	5.4117(8)	5.4138(0)
Particle size (nm)	14.86	21.65	16.67	13.88	13.49	13.78	20.16	21.53
RMS strain	1.25 × 10^−5	8.33 × 10^−4	2.25 × 10^−4	1.25 × 10^−5	7.68 × 10^−5	3.14 × 10^−4	1.25 × 10^−4	1.07 × 10^−3
Ce–O bond length (Å)	2.3372(7)	2.3391(0)	2.3402(4)	2.3410(6)	2.3419(6)	2.3426(5)	2.3433(7)	2.3442(4)
Density (g cm^−3)	7.268	7.312	7.332	7.354	7.376	7.399	7.453	7.505
Rwp (%)	5.42	4.34	5.26	5.79	3.69	3.61	4.34	5.03
Rexp (%)	4.63	3.91	4.69	5.03	3.29	3.11	3.67	4.37
GOF	1.17	1.11	1.12	1.15	1.12	1.16	1.18	1.15

---

The Rietveld analysis indicated that each sample had the cubic fluorite structure with space group Fm3̄m. In this structure, cerium ions occupy the vertices and face of the cubic unit cell. Each cerium ion (Ce⁴⁺) is co-ordinated with eight oxygen ions (O²⁻) arranged in a perfect cube, while each oxygen ion is surrounded by four cerium ions in a tetrahedral arrangement. This structure is often described as a cubic closed packing of cerium ions with oxygen ions occupying all tetrahedral holes.²³ The crystal structure of pure ceria is shown in Fig. 2(a). All the cerium ions (Ce⁴⁺) are situated at site 4a with the atomic co-ordinate (0,0,0), and the oxygen ions (O²⁻) are at site 8c, corresponding to the (1/4, 1/4, 1/4) position. All the ion positions are fixed during the whole refinement process. Generally, when the fluorite structured ceria is doped with a trivalent cation such as Dy³⁺, one oxygen vacancy is formed for every two trivalent cations for charge neutrality, which is represented by Kröger–Vink notation:

Fig. 2 The crystal structure of (a) pure ceria and (b) doped ceria.

Here Dy′_Ce indicates one Ce⁴⁺ site occupied by a Dy³⁺ ion, and represents the oxygen vacancy. The defect structure of the doped ceria is shown in Fig. 2(b). Here, the occupancy of Ce⁴⁺ ions in the 4a site and O²⁻ ions in the 8c site of undoped ceria are 0.9989(7) and 0.9859(1) respectively (Table 1). In doped ceria, the occupancy of Ce⁴⁺ ions decreases with the doping concentration, and the occupancy of dopant ions (Dy³⁺) in the 4a site increases. The occupancy of O⁻² ions at the 8c site decreases with the doping concentration of Dy³⁺ ions, which indicates a higher number of oxygen vacancies. The formation of these oxygen vacancies has been confirmed in earlier studies.^24–27 Fig. 3 shows the variation of the lattice parameters of the Ce_1−xDy_xO_2−δ (x = 0.00–0.50) samples as a function of total dopant concentration (x). It can be seen that the lattice parameter increases with dopant concentration, which is due to the fact that the ionic radius of Dy³⁺ (1.027 Å) is greater than the ionic radius of Ce⁴⁺ (0.97 Å). It can be seen from Fig. 3 that for the Ce_1−xDy_xO_2−δ system, the lattice parameter increases linearly with increasing Dy³⁺ concentration up to x = 0.25, following Vegard's law.²⁸ After x = 0.25, the lattice parameter of the Ce_1−xDy_xO_2−δ system also increases linearly, but the rate of increase is different. Using a least-squares fitting algorithm, a linear relationship was obtained between the lattice parameters (a) and dopant concentration (x). These can be represented as

a(x, 0 ≤ x ≤ 0.25) = 5.39771 + 0.04369x (4)

and

a(x, 0.3 ≤ x ≤ 0.5) = 5.40451 + 0.01847x (5)

Fig. 3 Variation of the lattice parameter with doping concentration x.

Similar results were found earlier for the Ce_1−xGd_xO_2−δ (0.05 ≤ x ≤ 0.4) system.²⁹ In the present study, the slower increase of the lattice parameters at higher concentrations (x > 0.25) can be attributed to the effect of the interaction between the dopant cations and the oxygen vacancies, which tends to contract the unit cell.³⁰ As the oxygen vacancy increases with doping concentration x, at higher doping concentrations the number of oxygen vacancies is much greater. Therefore, the interaction between the oxygen vacancies and dopant ions is greater at higher concentrations. At higher doping concentrations, the oxygen vacancies and defect associations appearing in the solid solutions are expected to have different interactions with the network ions, and the oxygen vacancy is believed to produce a lattice contraction rather than a defect association.³¹ The RMS strain for the sample Ce_0.8Dy_0.2O_2−δ shows a minimum value of 1.25 × 10⁻⁵. The Ce–O bond length of the system was also evaluated by Rietveld analysis and was found to increase with x, i.e. the change in the lattice parameter demonstrates the same behavior as the Ce–O bond length change. During the formation of rare earth doped ceria solid solutions, several defect reactions can occur. Among these, the oxygen vacancy model is very important, and is represented by the Kröger–Vink notation as given earlier. With the help of the oxygen vacancy model of doped ceria, we can determine the density of the system Ce_1−xDy_xO_2−δ (x = 0.00–0.50) using the following equation:

where M_Dy, M_Ce and M_O are the atomic weights of Dy, Ce and oxygen, repectively; N_A is Avogadro's number, and a is the lattice parameter. The values of the densities are given in Table 1 and are found to increase with doping concentration, as the atomic weight of Dy (162.5) is greater than that of Ce (140.11).

3.2. Energy dispersive X-ray analysis

The composition of the obtained system was analyzed by means of energy dispersive X-ray analysis (EDAX). Fig. 4(a)–(d) show the EDAX spectra for the compositions x = 0.00, x = 0.10, x = 0.20 and x = 0.50 respectively. The presence of major chemical elements, namely cerium, dysprosium and oxygen, in the prepared samples was confirmed from this analysis. The percentages of the Dy/Ce values are given in the inset of Fig. 4(a)–(d). The doped ceria did not deviate from their initial stoichiometry and matched well with the initial degree of Dy substitution. The EDAX spectrum clearly shows that oxygen content in the Ce_1−xDy_xO_2−δ system decreases with doping concentration, i.e. the oxygen vacancies increase with doping concentration. This result is in good agreement with the Rietveld analysis results discussed earlier.

Fig. 4 Energy dispersive X-ray analysis (EDAX) for (a) x = 0.00, (b) x = 0.10, (c) x = 0.20 and (d) x = 0.50. The percentage of Dy/Ce values are given in the inset.

3.3. Transmission Electron Microscopy (TEM) studies

The nanostructures of the samples were further characterized by transmission electron microscopy. The nanoflakes for the sample x = 0.2 are distributed uniformly, as observed in the bright field TEM image of Fig. 5(a). All the samples show similar nanostructures, with negligible size variation with composition. The crystallite size distribution for the sample x = 0.2 is shown in the inset of Fig. 5(a). It can be inferred that the average crystallite size is ∼16.84 nm, indicating that the sample preparation is successful in producing such nanostructures. In Fig. 5(b), the lattice fringe pattern is shown for the composition x = 0.2. The fast Fourier transform (FFT) of the embraced zone is shown in the inset of Fig. 5(b). At least three different pairs of bright spots are found, and these spots are identified as reflections from the (111), (002) and (11−1) lattice planes, as shown in the inset of Fig. 5(b). The sharp and bright spots further confirmed the cubic symmetry and good crystallinity of the sample. Using SAED studies, D. R. Ou et al. have shown an increase in the local ordering of oxygen vacancies with increasing doping concentration in lanthanide doped ceria.³² In Fig. 5(c) the simulated lattice pattern is also shown, with prominent lattice planes orientated along the (111) direction. It can be inferred that the lattice fringe in Fig. 5(c) consists of the (111), (002) and (11−1) planes, as previously suggested by the FFT pattern. To obtain more information, we have analyzed the atomic model using the XRD refinement results. Fig. 5(c) contains all of these lattice planes with a viewing direction along [−110], as suggested by the atomic model in Fig. 5(d). It can be noted that Dy³⁺ is partially occupying the Ce⁴⁺ site, so these cations cannot be isolated; however, the position of the cation (Ce⁴⁺/Dy³⁺) is detectable, as observed in Fig. 5(c) and (d).

Fig. 5 (a) Indicates the distribution of nanoflakes for the composition x = 0.2. The crystallite size distribution is also shown in the inset of (a). In (b) the lattice plane is shown. The FFT image is also shown in the inset of (b). The simulated lattice pattern is shown in (c). In (d) the atomic model indicates the orientation of the atoms. The gray spheres in (d) indicate the Ce⁴⁺/Dy³⁺ atoms, whereas darker spheres are O²⁻.

3.4. UV-vis spectroscopy

Fig. 6(a) shows the UV-VIS absorption spectra recorded for pure and doped ceria. It can be seen that there is a strong absorption band below 400 nm in the spectra for all the samples, which is due to the charge transfer from O⁻²(2p) to Ce⁴⁺(4f) orbitals in CeO₂.³³ However, there is no absorption in the visible region. The optical band gap values for the Ce_1−xDy_xO_2−δ (x = 0.00–0.50) system can be estimated from the absorption spectra following Tauc's rule:³⁴

αhν = A(hν − E_g)ⁿ (7)

where α is the absorption co-efficient, hν is the photon energy, E_g is the band gap energy, A is a constant and n can have values of 1/3, 1/2, 2, and 3 for the direct forbidden, direct allowed, indirect allowed, and indirect forbidden transitions respectively. The band gap corresponding to the direct transition was obtained by extrapolating the linear portions of (αhν)² versus the hν curves to (αhν)² equal to zero. A plot of (αhν)² as a function of photon energy hν for the sample Ce_0.75Dy_0.25O_2−δ is shown in Fig. 6(b). The calculated values of E_g for all the samples are given in Table 2. Undoped ceria shows the highest band gap value of 2.750 eV, and for Dy³⁺ doped ceria the values of the band gap decrease with dopant concentration x. Thus, the absorption spectra of Dy³⁺ doped ceria nanocrystals exhibit red shifts compared to that of pure ceria. In CeO₂, all valance Ce states, including the 4f states, are empty, and the system is a wide gap insulator with a measured fundamental band gap of 6.0 eV between the valance and conduction bands; this is formed predominantly by the O⁻² (2p) to Ce⁴⁺ (5d) states respectively.³⁵ The vacant 4f states lie in the gap. However, in our present study, the band gap value of CeO₂ is much lower than 6.0 eV. This is because a small amount of Ce³⁺ is present at the surface of CeO₂ ³⁶ and one electron per Ce atom populates a Ce 4f state, resulting in a decrease in the band gap value of ceria. The co-existence of a small amount of Ce³⁺ ions was also confirmed by XPS analysis.³⁷ The red shift of the direct band gap with x can be explained in several ways. Firstly, when Dy³⁺ ions are incorporated into the ceria lattice, the valency changes from Ce⁴⁺ to Ce³⁺ ions decrease due to the replacement of Ce³⁺ ions by trivalent Dy³⁺ ions, as confirmed by several authors using XPS.^38–40 The substitution of Ce³⁺ ion with Dy³⁺ ion increases with doping concentration, and this substitution increases the oxygen vacancy concentration due to a charge compensation mechanism, as discussed earlier. Secondly, the red shift may be due to the presence of oxygen defect levels between the O2p and Ce4f levels that capture the excited electrons and decrease the effective band gap.⁴¹ Lastly, the doping of Dy ions creates ground and excited f-energy states in the mid band gap of ceria. These energy states of Dy accept many of the excited electrons coming from the O2p level.¹¹ This ultimately leads to effective reduction in the band gap, i.e. a red shift.

Fig. 6 (a) The UV-VIS absorption spectra for pure and doped ceria Ce_1−xDy_xO_2−δ (x = 0.00–0.50) and (b) the plot of (αhν)² as a function of photon energy hν for the sample Ce_0.8Dy_0.2O_2−δ.

Table 2 The values of the band gap (E_g) for the Ce_1−xDy_xO_2−δ samples (x = 0.00–0.50). The errors after the third decimal are indicated inside parentheses

Samples	Band gap (eV)
CeO2	2.750(5)
Ce0.9Dy0.1O2−δ	2.714(1)
Ce0.85Dy0.15O2−δ	2.685(4)
Ce0.8Dy0.2O2−δ	2.590(3)
Ce0.75Dy0.25O2−δ	2.529(2)
Ce0.7Dy0.3O2−δ	2.516(1)
Ce0.6Dy0.4O2−δ	2.511(8)
Ce0.5Dy0.5O2−δ	2.471(5)

---

3.5. Raman spectroscopy

The Raman spectra of sintered samples Ce_1−xDy_xO_2−δ (x = 0.0–0.5) are shown in Fig. 7. These spectra exhibit a very intense Raman band centered at 462 cm⁻¹ to 484 cm⁻¹, as listed in Table 3. These bands were attributed to the Raman-active vibrational mode F_2g of the fluorite-type structure, which can be viewed as a symmetrical stretching vibration of oxygen atoms around the Ce³⁺ ions⁴² and is sensitive to the crystalline symmetry.⁴³ Table 3 also reveals that the F_2g mode shifts towards higher wavenumbers with increasing concentration of Dy³⁺ cations (i.e. with x). This shift is due to the increase in the number of oxygen vacancies, i.e. the decrease in the amount of oxygen ions bound to Ce or Dy ions.⁴⁴ Therefore, the number of oxygen vacancies increases in the Ce_1−xDy_xO_2−δ system (x = 0.0–0.5) with x, and this is in good agreement with the Rietveld analysis result. A second order Raman band below 400 cm⁻¹ and above 500 cm⁻¹ was observed, which is due to the extrinsic oxygen vacancies introduced into the ceria when the Ce⁴⁺ ions are replaced by Dy³⁺ ions. These Raman bands are also due to defect spaces such as M₄O_v and O₆O_v type complexes (M = metal ion and O_v = oxygen vacancy), where an M₄O_v type complex consists of an oxygen vacancy surrounded by four nearest neighbor metal ions and an O₆O_v type complex consists of an oxygen vacancy surrounded by six next nearest neighbor oxygen ions. These second order Raman bands below 400 cm⁻¹ were also observed in earlier studies.⁴⁵ The relative intensity of these bands also increases with the doping concentration of Dy³⁺ cations. For pure ceria, a single intense band centered at 462 cm⁻¹ is observed, which signifies that there is apparently no extrinsic oxygen vacancy. As shown in Fig. 7, for all the doped samples, there is a D band above 500 cm⁻¹ which splits into D₁ and D₂ bands for the samples x = 0.1–0.4. The D₁ and D₂ bands were merged into a broad single band for the sample x = 0.5. The center of the D₁ and D₂ bands shifts towards higher wavenumbers with the concentration of Dy³⁺ cations. These disordered D₁ and D₂ bands were used as a powerful tool to investigate the association of the formation of defects with the decrease in the total lattice energy in ceria based materials.⁴⁶ Hence, the D₂ bands from 597 cm⁻¹ to 610 cm ⁻¹ are attributed to defect spaces with O_h symmetry, which include a Dy³⁺ atom in 8-fold co-ordination of O²⁻ but do not contain any O²⁻ vacancies. The D₁ bands from 552 cm⁻¹ to 576 cm⁻¹ were assigned to defect spaces with symmetries other than O_h symmetry, including O²⁻ vacancies in the and complexes. Both the D₁ and D₂ bands shift towards higher wavenumbers with increasing concentration of Dy³⁺ ions, and the shift of D₁ is assigned to the increase of the complex compared to that of the complex. The ratio of the intensities of the different bands is listed in Table 3. The ratio of I_F2g/I_D1 and I_F2g/I_D2 decreases with increasing x, which is related to the degree of defect sites on CeO₂. This also indicates a higher number of oxygen vacancies with higher doping concentrations.⁴⁷ According to Nakajima et al.,⁴⁸ a low ratio of I_D1/I_D2 indicates that Ce³⁺ ions preferentially locate in a Ce³⁺O₈ type complex, and a higher value of this ratio indicates an increase in the concentration of the amalgamated defects of O²⁻ vacancies in Dy³⁺O₈ type complexes. S. F. Wang et al.⁴⁹ and Z. D. Dohčević-Mitrović et al.⁵⁰ have also shown the increase of oxygen vacancies with doping concentration in rare earth doped ceria solid solutions using Raman spectroscopy. The shift of the Raman bands and the change in the intensity ratio with doping concentration also confirms the formation of solid solutions in our present study by the citrate auto-ignition method.

Fig. 7 Raman spectra of sintered samples Ce_1−xDy_xO_2−δ (x = 0.0–0.5).

Table 3 Positions of different Raman bands and intensity ratios of different Raman bands for the Ce_1−xDy_xO_2−δ samples (x = 0.00–0.50)

Samples	Positions of Raman bands (cm^−1)			IF2g/ID1	IF2g/ID2	ID1/ID2
	F2g	D1	D2
CeO2	462	—	—	—	—	—
Ce0.9Dy0.1O2−δ	463	552	597	12.81	14.22	1.09
Ce0.8Dy0.2O2−δ	465	558	599	6.00	7.53	2.24
Ce0.7Dy0.3O2−δ	467	563	600	3.13	3.76	1.20
Ce0.6Dy0.4O2−δ	472	571	605	2.01	2.19	1.08
Ce0.5Dy0.5O2−δ	484	576	610	1.51	1.51	1.00

---

3.6. Electrical conductivity

Fig. 8(a) shows the variation of the real part σ′(ω) of complex conductivity as a function of frequency at a temperature of 525 °C for the Ce_1−xDy_xO_2−δ system (0.0 ≤ x ≤ 0.5). This figure reveals that conductivity spectra of this system consists of two parts, namely a frequency independent part in the low frequency region which corresponds to the DC conductivity caused by random hopping of the ions, and a frequency dependent part in the high frequency region which corresponds to the AC conductivity caused by the correlated forward backward hopping motion of the charge carriers among the localized sites.⁵¹ Therefore, the conductivity spectra can be well described by the following equation:

σ′ = σ_dc + σ_ac (8)

Fig. 8 (a) The variation of the real part σ′(ω) of complex conductivity as a function of frequency at a temperature of 525 °C for all the samples, (b) the variation of σ(0) with doping concentration at different temperatures and (c) Arrhenius plot of the system Ce_1−xDy_xO_2−δ (x = 0.10–0.50).

This spectrum also shows the similar nature of all the compositions. The Random free-energy Barrier Model (RBM), proposed by Dyre,⁵² describes the frequency dependent conductivity over a wide range of frequencies in disordered solids at constant temperature. This model is based on the determination that DC conductivity is more thermally activated than AC conductivity. We used RBM to evaluate the DC conductivity or the total conductivity. According to RBM, the complex conductivity σ*(ω) is given by

where σ(0) is the DC conductivity and is the attempt frequency to overcome the highest free energy barrier. The real part of σ*(ω) has been used to fit the conductivity spectra, as shown in Fig. 8(a). The variation of σ(0) with the doping concentration of Dy³⁺ for different temperatures is shown in Fig. 8(b). This figure reveals that the DC conductivity increases with doping concentration and shows a maximum value for x = 0.20; a further increase of the doping concentration decreases the conductivity. The oxygen vacancies inside the grain and grain boundary control the whole conduction process. This variation may be due to the number of oxygen vacancies present in the system and the interaction between the oxygen vacancies and dopant cations. As discussed earlier, the oxygen vacancies increase with doping concentration; therefore, conductivity is expected to increase with doping concentration. At higher doping concentrations, the number of oxygen vacancies will be greater, so there may be strong interactions between these vacancies and Dy³⁺ ions. Therefore, the motion of free oxygen vacancies at higher doping concentrations should be limited, and conductivity decreases. Fig. 8(c) shows the temperature dependence of DC conductivity σ(0), which obeys the Arrhenius equation given bywhere σ₀ is the pre-exponential factor, being a constant in a certain temperature range, K_B is Boltzmann's constant, T is the absolute temperature and E_a is the activation energy for DC conduction. E_a can be calculated easily from the slope of the Arrhenius plot. It is observed in Fig. 8(c) that the DC conductivity increases with temperature, which indicates that oxygen ion conduction in these compositions is a thermally activated process. The activation energies for DC conduction are listed in Table 4. The activation energy shows a minimum value for the sample x = 0.20, which shows the maximum conductivity. In another study by S. Kuharuangrong,⁵³ the activation energies for x = 0.10, x = 0.20 and x = 0.30 were reported as 1.06 eV, 1.11 eV and 1.15 eV respectively, and the composition x = 0.30 showed the highest conductivity among all the compositions. These activation energy values are very close to those found for our system. Again, according to S. Acharya,¹⁵ the composition x = 0.15 shows the lowest activation energy (0.86 eV) and the highest conductivity (7.42 × 10⁻² S cm⁻¹). A. K. Baral et al.²⁷ had reported the activation energy and conductivity at 550 °C for the composition x = 0.20 in their study as 1.16 eV and 1.36 × 10⁻⁴ S cm⁻¹, respectively. However, in our present system, the composition x = 0.20 shows a lower activation energy and higher conductivity at 550 °C (5 × 10⁻⁴ S cm⁻¹) than the previous study by A. K. Baral et al. Again, Y. Wang et al.⁵⁴ reported the activation energy and conductivity for the composition x = 0.10 in their study as 0.79 eV and 2 × 10⁻⁴ S cm⁻¹, respectively. Therefore, our conductivity and activation energies are comparable to previously reported studies. The activation energy and conductivity values of our present study and previous studies are also listed in Table 4. The scaling behavior of the conductivity spectra shows the effect of temperature on the conduction mechanism. The conductivity spectra of the compositions obey the time–temperature superposition principle (TTSP), i.e. all the conductivity spectra at different temperatures are superimposed on a single master curve. In the case of the real part of the complex conductivity, the TTSP can be represented by the following scaling law:⁵⁵

Table 4 The values of activation energy (E_a) and conductivities for the samples Ce_1−xDy_xO_2−δ (x = 0.10–0.50). The errors after the second decimal are indicated inside parentheses

Sample	Activation energy (eV)	Conductivity at 550 °C (Ω^−1 cm^−1)
Ce0.9Dy0.1O2−δ	1.12(2)	5 × 10^−5
	0.79 (ref. 54)	2 × 10^−4
Ce0.85Dy0.15O2−δ	1.10(9)	3 × 10^−4
	0.86 (ref. 15)	7.42 × 10^−2
Ce0.8Dy0.2O2−δ	1.10(5)	5 × 10^−4
	1.16 (ref. 27)	1.36 × 10^−4
Ce0.75Dy0.25O2−δ	1.15(8)	3.3 × 10^−4
Ce0.7Dy0.3O2−δ	1.19(8)	2.9 × 10^−4
	1.15 (ref. 53)
Ce0.6Dy0.4O2−δ	1.21(4)	8 × 10^−5
Ce0.5Dy0.5O2−δ	1.46(2)	1 × 10^−5

---

The scaling function F is independent of both the temperature and composition. Fig. 9(a) shows the superposition of all the curves on a master curve for x = 0.20. Similar behavior was also found for other compositions. This behavior simply indicates that the conduction mechanism (movement of oxygen ions through the crystal lattice as a result of thermally activated hopping of the oxygen ions moving from a crystal lattice site to another crystal lattice site) does not depend on temperature, i.e. the change in temperature only changes the number of charge carriers without changing the conduction mechanism.⁵⁶ Fig. 9(b) shows the scaled spectra for different compositions for a particular temperature, which shows the superposition of all the curves on a single curve. This indicates the doping concentration independence of the conduction mechanism. More clearly, the migration of charge carriers in our present system takes place through a simple hopping mechanism. The only likely migration events involve an oxygen ion hopping to a vacancy in a nearest neighbor or a next nearest neighbor site, thus exchanging its place with the vacancy. The increase of the doping concentration only changes the number of oxygen vacancies; the conduction mechanism, as mentioned above, remains unchanged.

Fig. 9 (a) Scaling of the real part of the ac conductivity σ′(ω) of the complex conductivity spectra σ*(ω) for Ce_0.8Dy_0.2O_2−δ at several temperatures and (b) conductivity master curve for different compositions at a temperature of 500 °C.

4. Conclusion

In summary, Dy doped ceria-based nanoparticles were obtained by the citrate auto-ignition method. The good stoichiometry of the atoms in the obtained samples was confirmed by EDAX. Rietveld analysis of the XRD data and HRTEM of the sintered samples confirmed their good crystallinity and single phase cubic fluorite structures with space group Fm3̄m. The variation of the lattice parameter with doping concentration tends to saturate at higher doping concentrations due to interactions between the oxygen vacancies and cations. The UV-VIS absorption measurements showed a red shift in the absorption peak positions with the concentration of Dy³⁺ ions, and were explained in terms of the compensation of Ce³⁺ ions, generation of oxygen vacancies and creation of f-energy states. The Rietveld analysis and the shift of the different Raman bands confirmed the increase of oxygen vacancies with doping concentration. The Raman spectra also reveal the presence of different defect spaces, such as M₄O_v, O₆O_v, Ce³⁺O₈ and Dy³⁺O₈ type complexes, including oxygen vacancies. The DC conductivity and activation energy vary with doping concentration due to oxygen vacancies and to interactions between the vacancies and the dopant cations.

Acknowledgements

One of the authors (AD) thankfully acknowledges the financial assistance from Department of Science and Technology (Govt. of India) (Grant no. SR/FTP/PS-141-2010). The authors (SA and AD) also acknowledge the instrumental support from DST (Govt. of India) under departmental FIST programme (Grant no. SR/FST/PS-II-001/2011) and University Grants Commission (UGC) for departmental CAS scheme.

Reference

1. B. C. H. Steele, Solid State Ionics, 2000, 129, 95–110.
2. E. Bekyarova, P. Fornasiero, J. Kaspar and M. Graziani, Catal. Today, 1998, 45, 179–183.
3. L. Zhaogang, L. Mei, H. Yanhong, W. Mitang and S. Zhenxue, J. Rare Earths, 2008, 26, 158–162.
4. Z.-P. Li, T. Mori, F. Ye, D. Ou, J. Zou and J. Drennam, J. Chem. Phys., 2011, 134, 224708.
5. B. Choudhury and A. Choudhury, Curr. Appl. Phys., 2013, 13, 217–223.
6. J. Ueda and S. Tanabe, J. Appl. Phys., 2011, 110, 073104.
7. M. Yashima, S. Kobayashi and T. Yasui, Faraday Discuss., 2007, 134, 369–376.
8. J. M. de Souza e Silva, M. Strauss, C. M. Maroneze, E. R. Souza, Y. Gushikem, F. A. Sigoli and I. O. Mazali, J. Mater. Chem., 2011, 21, 15678–15685.
9. Z. P. Li, T. Mori, F. Ye, D. Ou, G. Auchterlonie, J. Zou and J. Drennan, J. Phys. Chem. C, 2012, 116, 5435–5443.
10. Z. P. Li, T. Mori, J. Zou and J. Drennan, Mater. Res. Bull., 2013, 48, 807–812.
11. M. Greenberg, E. Wachtel, I. Lubomirsky, J. Fleig and J. Maier, Adv. Funct. Mater., 2006, 16, 48–52.
12. T. Taniguchi, T. Watanabe, N. Sugiyama, A. K. Subramani, H. Wagata, N. Matsushita and M. Yoshimura, J. Phys. Chem. C, 2009, 113, 19789–19793.
13. G. B. Balazs and R. S. Glass, Solid State Ionics, 1995, 76, 155–162.
14. H. Inaba and H. Tagawa, Solid State Ionics, 1996, 83, 1–16.
15. S. A. Acharya, J. Power Sources, 2011, 198, 105–111.
16. S. Anirban and A. Dutta, J. Phys. Chem. Solids, 2015, 76, 178–183.
17. S. Sain, S. Patra and S. K. Pradhan, Mater. Res. Bull., 2012, 47, 1062–1072.
18. H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71.
19. L. Lutterolti, P. Scardi and P. Maistrelli, J. Appl. Crystallogr., 1992, 25, 459–462.
20. R. A. Young in, The Rietveld method, ed, R. A. Young, Oxford University Press/IUCr, 1996, pp. 1–38.
21. L. B. McCusker, R. B. Von Dreele, D. E. Cox, D. Louer and P. Scardi, J. Appl. Crystallogr., 1999, 32, 36–50.
22. N. C. Popa, J. Appl. Crystallogr., 1998, 31, 176–180.
23. S. Gangopadhyay, D. D. Frolov, A. E. Masunov and S. Seal, J. Alloys Compd., 2014, 584, 199–208.
24. M. Nakayama and M. Martin, Phys. Chem. Chem. Phys., 2009, 11, 3241–3249.
25. S. J. Hong, K. Mehta and A. V. Virkar, J. Electrochem. Soc., 1998, 145, 638–647.
26. T. Mori, T. Kobayashi, Y. Wang, J. Drennan, T. Nishimura, J. G. Li and H. Kobayashi, J. Am. Ceram. Soc., 2005, 88, 1981–1984.
27. A. K. Baral and V. Sankaranarayanan, Nanoscale Res. Lett., 2010, 5, 637–643.
28. L. Vegard and H. Dale, Z. Kristallogr., 1928, 67, 148–162.
29. D. Pérez-Coll, P. Núñ ez, J. C. Ruiz-Morales, J. Peñ a-Martíez and J. R. Frade, Electrochim. Acta, 2007, 52, 2001–2008.
30. S. Omar, E. D. Wachsman and J. C. Nino, Solid State Ionics, 2008, 178, 1890–1897.
31. L. Li, G. Li, Y. Che and W. Su, Chem. Mater., 2000, 12, 2567–2574.
32. D. R. Ou, T. Mori, F. Ye, J. Zou, G. Auchterlonie and J. Drennan, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 024108.
33. Y.-W. Zhang, R. Si, C.-S. Liao, C.-H. Yan, C.-X. Xiao and Y. Kou, J. Phys. Chem. B, 2003, 107, 10159–10167.
34. S. L. S. Rao, G. Ramdevudu, Md. Shareefuddin, A. Hameed, M. N. Chary and M. L. Ro, Int. J. Eng. Sci. Res. Technol., 2012, 4, 25–35.
35. E. Wuilloud, B. Delley, W. D. Schneider and Y. Baer, Phys. Rev. Lett., 1984, 53, 202–205.
36. L. Wu, H. J. Wiesmann, A. R. Moodenbaugh, R. F. Klie, Y. Zhu, D. O. Welch and M. Suenaya, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 125415.
37. G.-R. Li, D.-L. Qu, L. Arurault and Ye-X. Tong, J. Phys. Chem. C, 2009, 113, 1235–1241.
38. K. Kuntaiah, P. Sudarsanam, B. M. Reddy and A. Vinu, RSC Adv., 2013, 3, 7953–7962.
39. Z. Wang, Z. Quan and J. Lin, Inorg. Chem., 2007, 46, 5237–5242.
40. C. Sun, H. Li, H. Zhang, Z. Wang and L. Chen, Nanotechnology, 2005, 16, 1454–1463.
41. A. H. Morshed, M. E. Moussa, S. M. Bedair, R. Leonard, S. X. Liu and N. El-Masry, Appl. Phys. Lett., 1997, 70, 1647–1649.
42. M. Sarkar, R. Rajkumar, S. Tripathy and S. Balakumar, Mater. Res. Bull., 2012, 47, 4340–4346.
43. I. Atribak, A. Bueno-López and A. García- García, J. Catal., 2008, 259, 123–132.
44. J. R. McBride, K. C. Hass, B. D. Poindexter and W. H. Weber, J. Appl. Phys., 1994, 76, 2435–2441.
45. E. C. C. Souza and E. N. S. Muccillo, J. Alloys Compd., 2009, 473, 560–566.
46. T. Taniguchi, T. Watanabe, N. Sugiyama, A. K. Subramani, H. Wagata, N. Matsushita and M. Yoshimura, J. Phys. Chem. C, 2009, 113, 19789–19793.
47. R. O. da Fonseca, A. A. A. da Silva, M. R. M. Signorelli, R. C. Rabelo-Neto, F. B. Noronha, R. C. C. Simões and L. V. Mattos, J. Braz. Chem. Soc., 2014, 25, 2356–2363.
48. A. Nakajima, A. Yoshihara and M. Ishigame, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 13297–13307.
49. S. F. Wang, C. T. Yeh, Y. R. Wang and Y. C. Wu, J. Mater. Res. Technol., 2013, 2, 141–148.
50. Z. D. Dohčević-Mitrović, M. J. Šćepanović, M. U. Grujić-Brojčin, Z. V. Popović, S. B. Bošković, B. M. Matovic, M. V. Zinkevich and F. Aldinger, Solid State Commun., 2006, 137, 387–390.
51. Raghvendra, R. K. Singh and P. Singh, J. Mater. Sci., 2014, 49, 5571–5578.
52. J. C. Dyre, J. Appl. Phys., 1988, 64, 2456–2468.
53. S. Kuharuangrong, J. Power Sources, 2007, 171, 506–510.
54. Y. Wang, T. Mori, J. G. Li and J. Drennan, J. Eur. Ceram. Soc., 2005, 25, 949–956.
55. B. Roling, A. Happe, K. Funke and M. D. Ingram, Phys. Rev. Lett., 1997, 78, 2160.
56. Raghvendra, P. Singh and R. K. Singh, J. Alloys Compd., 2013, 549, 238–244.

---