Determination of midodrine hydrochloride via Hantzsch condensation reaction: a factorial design based spectrophotometric approach

Abstract

A set of experimental designs was executed to attain the optimal reaction parameters of chemical derivatization of midodrine hydrochloride (MD·HCl) in oral formulas via a Hantzsch condensation reaction. The process variables, such as reaction temperature, heating time, reagent volume, and pH were screened by operating a 2-level full factorial design. Variables proved to be significant (p < 0.05) were warily attuned utilizing a response surface methodology (RSM) with a face-centered central composite design. The suggested model represented a perfect example for probing the efficiency of factorial designs in optimizing the reaction conditions and maximizing the output. In this itinerary, the developed model allowed the evaluation of main, interaction and quadratic effects of tested variables. A linear calibration curve was obtained in the range of 2.00–18.00 μg mL⁻¹ with a high value for the coefficient of determination (R² = 0.9999). Statistical validation of the proposed technique was done using ANOVA in two successive steps. Moreover, a D-optimality design was employed to minimalize the variation in the regression coefficients of the fitted model. The optimized technique was used to determine MD·HCl in tablets and oral drops using a simple extraction procedure prior to measuring the absorbance at 330 nm. The results obtained were in good agreement with the label claim with no interference from adjuvants commonly co-formulated with the drug. Inter- and intra-day precision, limits of detection and quantification, and relative standard deviation have been assessed following ICH guidelines for evaluation of analytical procedures, and the results obtained were satisfactory.

---

1. Introduction

Midodrine hydrochloride (MD·HCl) is chemically recognized as 2-amino-N-[2-(2,5-dimethoxyphenyl)-2-hydroxyethyl]ethanimidic acid hydrochloride (Scheme 1).¹ Being well known as an α-adrenergic agonist, MD·HCl is widely used as an OTC drug, especially in the Middle East, for treatment and management of orthostatic hypotension, and autonomic neuropathy with almost no effects on both cardiac stimulation or central nervous system. Though MD·HCl has no effect on β-adrenergic receptors, it is contraindicated in patients with severe organic cardiovascular disease.^1–4 A literature review shows a limited number of spectrophotometric procedures for determination of MD·HCl.^5,6 Spectroscopic investigation of MD·HCl was performed using FTIR, FT-Raman and UV-vis.⁷ Other methods reported in the literature include: electrophoresis,⁸ HPLC,⁹ GC-MS,¹⁰ and potentiometry.¹¹

Scheme 1 Midodrine hydrochloride.

The Hantzsch reaction, a well-known multi-component assembly process, is a famous pathway for pyrrole and pyridine synthesis. The process in general involves a reaction between an aldehyde (1 equivalent), a β-ketoester (2 equivalents) and a primary amine.¹² Making use of the formation of a colored condensation product, the Hantzsch reaction has been employed for determination of many primary amine containing drugs.^13–16 In the current proposal, reaction of acetyl acetone (β-diketone) together with formaldehyde (aldehyde), and MD·HCl (primary amine), to produce a yellow colored dihydrolutidine derivative, was used as a basis for building a validated spectrophotometric procedure for determination of MD·HCl both in pure form and in different formulations.

For this reaction, different factors were found to affect the anticipated response. These variables include, but are not limited to, the temperature, heating time, reagent volume, and pH. The traditional way for investigating such a large number of factors depends on fixing all variables and changing the factor under consideration. This stratagem, irrespective of being time, effort, and chemical consuming, shows more critical defects such as the inability to assess the impact of interactions between the different variables, and the arithmetical implication of each factor on the presumed response. These flaws impose the usage of a multivariate system in which the intensity of all variables is altered contemporarily. Using such a system widens the domains explored, moreover, it pledges the quality of information collected for each point through their influence.

To have such a system, the first phase is to ‘screen’ all the involved variables to recognize the ‘significant’ factor, which is identified as an ‘element’ with an impact that exceeds the noise level. This approach can be attained using a reduced design of experiments (DoE), such as 2-level full/fractional factorial, and Plackett–Burman (PBD) designs. The second phase in this process is the ‘optimization’ where a 2^nd order response surface to the factors that have been screened and labelled ‘significant’ is patterned. Models such as central composite (CCD), Box–Behnken (BBD), and Doehlert designs (DD) are commonly used for this purpose.^17–20

In the current investigation, and with the purpose of augmenting the lineal range for the interaction between MD·HCl, acetylacetone and formaldehyde via Hantzsch reaction, the screening process has been done employing a 2-level full factorial design (FFD). For tweaking the response, the central composite design (CCD) was utilized.

2. Experimental

2.1. Materials and reagents

All reagents were of analytical grade. Water was always doubly distilled. Midodrine hydrochloride (MD·HCl) and sodium acetate trihydrate were purchased from Sigma-Aldrich (USA); MD·HCl was used as received. Formaldehyde solution (37% w/w) was purchased from Merck (Darmstadt, Germany). Acetylacetone was purchased from El-Nasr Chemical Co. (Cairo, Egypt). The following pharmaceutical formulations were purchased from local pharmacy stores: Midodrine® oral drops and Midodrine® tablets; Nile Pharma. Co., Egypt, labelled to contain 2.5 mg and 1% of MD·HCl respectively.

2.2. Reagent preparation

Acetylacetone–formaldehyde reagent: into a 25 mL volumetric flask, a volume of 10 mL of acetic acid–sodium acetate buffer (pH 4.00), 2.1 mL of acetylacetone, 5.0 mL of formaldehyde were mixed, and the volume was made up to the mark with purified water. The reagent should be freshly prepared.

Aqueous stock solution was prepared as 1 mg mL⁻¹. Further dilutions with the same solvent were carried out to obtain different working solutions.

2.3. Apparatus

A Shimadzu 260-UV recording spectrophotometer with a 10 mm quartz cell was used for all absorbance measurements. A Jenway pH meter equipped with a glass combination electrode (UK) was used for adjusting the pH of working solutions. A thermostatically controlled water bath (MLV, Salvis AG Emmenbruck, Luzern, Germany) was used throughout the work. Minitab®17 software (Minitab Inc., State College, Pennsylvania, USA) was used for screening and optimizing the factorial design. PSI plot software was used to perform curve fittings when necessary.

2.4. Procedure for pure pharmaceuticals

Aliquots of standard MD·HCl solution ranging between 20 and 180 μg mL⁻¹ were transferred into 10 mL test tubes. Then 0.2 mL of the reagent (prepared in acetate buffer of pH 4.00) was added into each test tube. The mixture was heated up in a boiling water bath (100.00 °C ± 2) for 5 minutes. The test tubes were cooled down to room temperature, quantitatively transferred into 10 mL volumetric flasks, and then the volume was made up to the mark with distilled water. The absorbance of the yellow colored complex was measured at 330 nm against a reagent blank similarly prepared.

2.5. Pharmaceutical formulations

Twenty tablets were pulverized and homogenized. An amount of the powder equivalent to 25 mg of MD·HCl was accurately weighed and transferred into a 25 mL flask. The drug was extracted four times with 5 mL distilled water. After extraction, the flask was washed a few times using a couple of mL of water, then, the combined washings and extracts were filtered into a 25 mL volumetric flask. The volume was made up to the mark with distilled water. The nominal content of the investigated drug in the tablets was determined as described in the procedure section. Similarly, 1 mL of the oral drops content was transferred into a 100 mL volumetric flask. Further dilutions to obtain working solutions were performed as described under the Experimental section.

2.6. Reference procedure

To validate the results obtained via the proposed procedure, a reference spectrophotometric technique (condensation with ninhydrin) was also used to analyze MD·HCl both in pure form and in formulations.⁶

2.7. Experimental design

All synthetic conditions that might affect the anticipated response (formation of a colored product with maximum absorbance) are listed in Table 1. Various investigational approaches were adopted to tune the values of inspected parameters. The target was to reduce the number of experiments needed while investigating the maximum number of factors. With variables being selected, and their domains being defined, the ordinary two phase setup (screening and optimization) was proposed. A 2-level FFD was asserted for the screening phase. Design generation was done using Minitab®17 software, with all variables being quantitative. As a screening design, FFD comprises runs at each probable combination at the delineated upper and lower domains for each variable, Table 1. A 2⁴-FFD (16 runs in the base design, 2 replicates, and 4 centre points in total added to the matrix of design) was developed keeping all factors free from aliasing. For optimization, a face-centred central composite design (FCC) was executed. A full factorial design with an additional design that has 32 cube points, 16 axial points and 4 centre points in axial and 8 in cube was used to generate the full face-centred design. Experiments were run in 2 replicates and in 2 base blocks. Each factor was tested at three levels. The best response was attained using a polynomial function and taking into consideration the linear, 2-way, as well as the quadratic interactions.

Table 1 Screened factors and response domains for a two-level (2⁴) full factorial design (FFD) premeditated for the Hantzsch reaction. The added central point isn’t shown.

Screened factor	Symbol	Level		Maximum absorbance of the product (Y)
		Low (−)	High (+)
Temperature (°C)	X1	25.00	100.00	0.602
Heating time (min)	X2	5.00	30.00	0.495
Reagent volume (mL)	X3	0.10	1.00	0.489
pH of acetate buffer	X4	2.40	5.60	0.493
Response	Y	Target

---

Each model structure was validated via the analysis of variance (ANOVA) at 95.0% confidence limits.

3. Results and discussion

3.1. Hantzsch reaction

Investigations of the chemistry behind the formation of a condensation product via the Hantzsch reaction have an extended history. A literature survey has shown that the formation of such a product, as shown in Scheme 2, occurs via the removal of three water molecules to form the yellow colored dihydrolutidine derivative.^14,15 In another proposal (reaction scheme is not shown), and as a first step, the lone pair of electrons available on the nitrogen atom from the candidate drug would attack the partially positively charged carbon atom of the aldehyde, with subsequent elimination of the first water molecule and formation of an imine. The β-dicarbonyl compound (keto form) would now attack the imine carbon that is positively charged. The last step is the formation of an intramolecular hydrogen bond between the carbonyl oxygen and the hydrogen attached to the drug nitrogen.²¹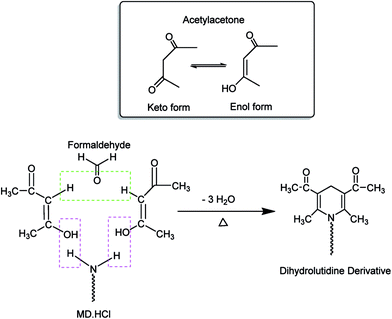

Scheme 2 A suggested reaction mechanism for the formation of a chromogen due to reaction of MD·HCl with an acetate buffered acetylacetone–formaldehyde mixture, the Hantzsch reaction.

3.2. Inspection of significant variables

As shown in Table 1; four variables were able to affect the interaction of MD·HCl with acetylacetone and formaldehyde measured by spectrophotometry. The implemented design allows determination of factors with the utmost impact on the process, i.e. the main factors. Moreover, and with the help of 2-level FFD, the joint effect of factors can be scrutinized.

As shown in the Pareto chart of standardized effects, Fig. 1, the four inspected factors extend beyond the absolute value of the effects, signifying that all are potentially significant, with reagent volume (C, RV, X3) having the highest influence on the product absorbance and pH (D, X4) having the lowest. The interaction (reagent volume × heating time) seems to be the most weighty factor compared to the rest of the interactions. The same conclusion was drawn employing half-normal plots of standardized effects, Fig. 2.

Fig. 1 Pareto chart for 2⁴ – full factorial design for the absorbance of the colored condensation product.

Fig. 2 Half-normal plot for absolute standardized effects. As shown in the graph, the interaction of (heating time × reagent volume) is the most influential variable, being the most distant from the noise line.

As was earlier mentioned, the proposed model assumptions were confirmed using ANOVA in two consecutive steps. In the first validation, all main effects and 2-way interactions are considered, while all higher-order interactions were removed (alpha = 0.05), Table 2. According to the data shown in the table, all initial assumptions of statistical significance of regression coefficients were validated with normality and goodness-of-fit being seen. The R² for the fitted model was 95.65% while the adjusted R² value was 93.65%. The regression equation for the proposed model in un-coded units is:

Y = 0.4801 + 0.000263Temp. − 0.01705HT − 0.4467RV − 0.0246pH − 0.000004Temp. × HT − 0.000042Temp. × RV + 0.000195Temp. × pH + 0.01396HT × RV + 0.000961HT × pH + 0.00967RV × pH + 0.2401center Pt (1)

Table 2 Analysis of variance (ANOVA) at 95% confidence level for a 2-level factorial design. The table shows results for factorial regression: Y versus X1: Temp., X2: HT, X3: RV, X4: pH, center Pt.

Source	DF^a	Adj SS^a	Adj MS^a	F-Value	p-Value
a DF is degrees of freedom, SS is sum of squares and MS is mean of squares. Significant factors (2-way interactions) (p-value = 0.05) appear in italic.
Model	11	0.815135	0.074103	47.93	0.000
Linear	4	0.394938	0.098734	63.86	0.000
X1: Temp.	1	0.040491	0.040491	26.19	0.000
X2: HT	1	0.167432	0.167432	108.30	0.000
X3: RV	1	0.179236	0.179236	115.93	0.000
X4: pH	1	0.007778	0.007778	5.03	0.034
2-Way interactions	6	0.215253	0.035875	23.21	0.000
X1: Temp. × X2: HT	1	0.000119	0.000119	0.08	0.784
X1: Temp. × X3: RV	1	0.000016	0.000016	0.01	0.920
X1: Temp. × X4: pH	1	0.004388	0.004388	2.84	0.105
X2: HT × X3: RV	1	0.197365	0.197365	127.66	0.000
X2: HT × X4: pH	1	0.011816	0.011816	7.64	0.011
X3: RV × X4: pH	1	0.001550	0.001550	1.00	0.327
Curvature	1	0.204944	0.204944	132.56	0.000
Error	24	0.037104	0.001546
Lack-of-fit	5	0.017449	0.003490	3.37	0.024
Pure error	19	0.019655	0.001034
Total	35	0.852239

---

In the re-analysis test, only variables which proved to be significant were re-analysed using ANOVA, see the normplot of residuals and residuals versus fit for the suggested model (Fig. 3a and b). The results obtained show constant variance, in agreement with tentative data.

Fig. 3 (a) Normplot of residuals for absorbance of the colored reaction product, dihydrolutidine derivative. (b) Residuals versus fits for absorbance of the colored reaction product. Plots were obtained by excluding variables proved to be non-significant according to the first ANOVA validation.

3.3. Optimization of significant variables (response surface designs)

In this phase, factors proved to be vital were introduced to Minitab®17 with the purpose of finding the “optimal” operating conditions. Levels of these factors were cautiously chosen to obtain an experimental domain that satisfies the experimental specifications. Central Composite Design (CCD) was used for this purpose.

According to the results obtained from the diagnostic 2⁴ full-factorial design, new levels for each single parameter were defined for the tuning trials. For this purpose, the reaction temperature was scanned in the range of 60–100 °C, the heating time was kept in the range of 5–25 min, the reagent volume was 0.1–0.5 mL, and the pH was tested in the range of 2.4–4.0. A central point for the newly defined ranges was added to compensate for a possible curved interaction between the different factors creating the star design.

The predictive 2^nd order polynomial model equation obtained was as follows:

Y = −0.277 + 0.00780Temp. − 0.00231HT − 0.956RV + 0.2175pH − 0.000025Temp. × Temp. + 0.000047HT × HT + 1.305RV × RV − 0.01807pH × pH − 0.000108Temp. × HT − 0.002252Temp. × RV + 0.000156Temp. × pH + 0.01604HT × RV − 0.002850HT × pH − 0.0618RV × pH (2)

According to this equation, the absorbance of the formed complex is directly proportional to the heating temperature (Temp.) and the pH in the studied range, with pH being more influential. On the other hand, the absorbance is inversely proportional to the reagent volume (RV) and the heating time (HT), with RV being more significant. The interactions: Temp. × HT, HT × pH, RV × pH, and Temp. × RV were found to decrease the absorbance, in contrast to the interactions Temp. × pH and HT × RV which increase the absorbance. Checking the quadratic terms and their coefficients reveals that RV has the highest influence on the anticipated absorbance followed by pH, indicating a probable curvature and a curvilinear effect on the response. As per the equation, Temp. and pH had a positive impact on the absorbance while their quadratic effects are negative, indicating that the absorbance value increases with the individual terms reaching a verge after which it starts to decrease, Fig. 4a and b.

Fig. 4 (a) Main effect plots and (b) interaction plots showing the effect of individual and 2-way interactions on the absorbance of the formed condensation product.

Two types of graphs were used to “pinpoint” the optimal conditions: the response surface (3D) and contour (2D) plots. As shown in Fig. 5, contour lines are produced when points that have the same absorbance are connected. On the other hand, 3D surface plots, Fig. 6, provide a stronger idea of the interactions compared to contour plots. Both representations reveal a good match with the results obtained employing the polynomial eqn (2).

Fig. 5 Contour plots for FCC design showing Y as a function of different variable interactions.

Fig. 6 3D Surface response plots for FCC design.

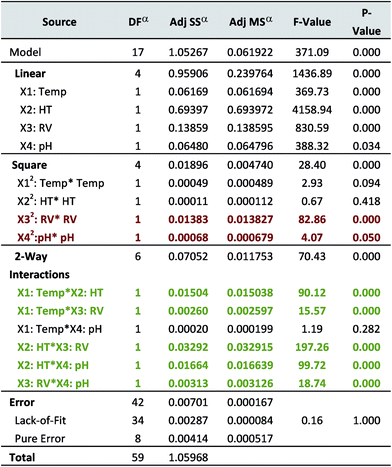
The quality of the proposed model was evaluated using ANOVA. According to Table 3, the obtained data shows that the suggested model signifies the phenomenon to a great extent and that the response was properly correlated to the variations in the factors. According to the ANOVA table, linear effects were statistically significant. Quadratic terms, X1² and X2² were not significant, compared to X3² and X4² which were significant. The 2-way interactions were significant except for the interaction between Temp. and pH (p = 0.282). The overall contribution of the terms to the proposed design was significant. The lack-of-fit, on the other hand, was not significant with a p-value much higher than the alpha level (0.05) (p = 1.000), an issue that is appropriate for fine-tuning studies. Based on these findings, model reduction is needed with the elimination of the non-significant variables. A second ANOVA test was performed and the following reduced polynomial equation was obtained:

Y = 2.055 + 0.000396Temp. − 0.001312HT − 21.65RV + 0.685pH + 30.48RV × RV − 0.0366pH × pH − 0.000001Temp. × HT − 0.000563Temp. × RV + 0.008018HT × RV − 0.000356HT × pH − 0.3861RV × pH (3)

Table 3 ANOVA for a FCC design and the associated probability values for absorbance of the condensation product

a DF is degrees of freedom, SS is sum of squares and MS is mean of squares. Significant factors (p-value = 0.05) appear colored.

---

The R² value for the reduced model was 99.24% and the adjusted R² was in good agreement with the predicted value, therefore, the developed model can be used to predict the absorbance of the condensation product even if the experiment was not done.

As shown in Fig. 7, the obtained histogram shows that no outliers exist in the obtained data. Based on the normal probability plot of residuals, data were normally distributed with residuals following a straight line. According to the residuals versus fits plot, the constant variance assumption is accomplished. The plot of residuals versus order of data is oscillating in an unsystematic pattern about the central line inferring that residuals are not interrelated to each other. Satisfying all these assumptions indicates that the produced coefficient approximations were not subjective and had a minimum variance.

Fig. 7 Normal probability plot, histogram, residuals versus fits, and residual versus order for the absorbance of the condensation product. Plots were obtained by excluding variables proved to be non-significant according to the first ANOVA validation performed on the proposed FCC design.

A D-optimality design was selected to minimize the variance in the regression coefficients of the fitted model. The insignificant terms were removed; the initial design was created using the sequential method and improved by the exchange method. As shown in Table 4, the condition number is high enough to confirm the high collinearity among the model terms. A large D-optimality value indicated that the variance between the regression coefficients has been minimized. A lower A-optimality value shows that average variance in the regression model has been reduced. The maximum prediction variance over the set of design points was minimized as indicated by a larger G-optimality value. Average leverage and maximum leverage were almost equal indicating that all points in the model have an equal influence.

Table 4 Optimal design output extracted from Minitab® 17. A full quadratic model was employed. Insignificant terms were removed from the proposed model

Parameter	Value
Condition number	33 122.2
D-optimality	3.15603 × 10^31
A-optimality	107 286
G-optimality (avg leverage/max leverage)	0.982053
V-optimality (average leverage)	0.2
Maximum leverage	0.203655

---

The optimization plot, as revealed in Fig. 8, provides the “optimum” solution for the contributing variable combinations. The conditions shown on the graph produced the best absorbance (target is maximized). The bottom section of the plot expresses the individual desirability (d) for each single factor. With a value of 0.97909, it can be inferred that the target response has been attained. As shown in the top row of Fig. 8, the value of composite desirability (D) is 0.9791 which is close to 1 denoting that the proposed settings (shown on the graph as Cur) have achieved the anticipated results.^22,23

Fig. 8 Desirability plot for the FCC design. The denoted current settings were employed to establish the calibration curve. The horizontal dashed blue lines represent the current response values. The vertical red lines on the graph represent the current settings.

3.4. Validation of the proposed analytical procedures

Validation of the proposed procedure was carried out in accordance with the International Conference on Harmonization (ICH) guidelines.²⁴ The following parameters were considered for the validation process:

3.4.1. Linearity and range. The linear range, detection limits, and standard analytical error are shown in Table 5. The proposed procedure shows a good linearity as revealed by the value of the coefficient of determination “R²”. LOD and LOQ were calculated as 3.3σ/s and 10σ/s respectively, where σ is the SD of the y-intercept of the regression line, and s is the slope. As shown in Table 5, values of LOD and LOQ for MD·HCl using the proposed technique were low enough to imply that the suggested procedure is suitable for determination of MD·HCl both per se and in the corresponding formulations. Data for applying the recommended procedure as imposed by the experimental design are shown in Table 6, with mean recoveries, SD and RSD being calculated.^25,26

Table 5 Optical and regression characteristics for the determination of MD·HCl using the proposed spectrophotometric procedure

Parameter	Value	Parameter	Value
a Regression equation: A = bC + a, where A is the absorbance, C is concentration in μg mL^−1, a is intercept, b is slope, Sb = SD of slope ± tSb = confidence limit for slope, Sa = SD of intercept ± tSa = confidence limit for intercept Sy/x = SD of the regression, SS is sum of squares.b LOD = limit of detection, LOQ = limit of quantification.
Wavelength, λmax (nm)	330	Slope (b)	0.04841
Linear range^a (μg mL^−1)	2.00–18.00	Intercept (a)	0.016098
Sb	0.000236	Coefficient of determination, R^2	0.999905
± tSb	0.000189	LOD^b (μg mL^−1)	0.208
Sa	0.002795	LOQ^b (μg mL^−1)	0.694
± tSa	0.002237	Residual SS	4.52 × 10^−5
Sy/x	0.003361	Regression SS	0.476514

---

Table 6 Application of the proposed analytical procedures for determination of MD·HCl in bulk powder

Amount taken (μg mL^−1)	Amount found (μg mL^−1)	% Recovery^a
a Average of 3 determinations.
2.00	1.99	99.50
4.00	4.03	100.75
10.00	9.90	99.00
12.00	12.07	100.60
16.00	16.00	100.00
18.00	17.98	99.90
Mean ± SD		99.96 ± 0.659
RSD		0.659

---

3.4.2. Accuracy and precision. The accuracy and precision of the suggested technique was determined for both pure samples and formulations. Evaluation was performed by measuring 3 different concentrations for 3–5 times within the same day (intra-day). Alternatively, every day accuracy and precision were calculated on three subsequent days (inter-day). All data were calculated at 95% confidence limits, and are shown in Tables 7 and 8.^27,28

Table 7 Inter-day and intra-day accuracy and precision for the determination of MD·HCl using the proposed procedure

Concentration (μg mL^−1)	Mean % recovery^a ± SD	RSD (%)	Er (%)
a Mean ± SD of 3 determinations.b The intra-day (n = 3), average of three concentrations of MD·HCl repeated three times within the same day.c The inter-day (n = 3), average of three concentrations of MD·HCl repeated three times in three successive days.
Intra-day precision and accuracy^b
4.00	99.58 ± 0.764	0.767	0.417
10.00	99.30 ± 0.265	0.266	0.700
12.00	100.19 ± 0.419	0.419	−0.194
16.00	99.75 ± 0.331	0.332	0.250
Inter-day precision and accuracy^c
4.00	98.25 ± 1.984	2.019	1.750
10.00	98.33 ± 1.172	1.192	1.667
12.00	100.67 ± 0.763	0.759	−0.667
16.00	98.92 ± 1.507	1.523	1.083

---

Table 8 Inter-day and intra-day accuracy and precision for the determination of MD·HCl in the corresponding formulations using the proposed spectrophotometric procedure^a

Midodrine® drops				Midodrine® tablets
Concentration (μg mL^−1)	Mean % recovery ± SD	RSD (%)	Er (%)	Concentration (μg mL^−1)	Mean % recovery ± SD	RSD (%)	Er (%)
a Mean ± SD of 3 determinations.b The intra-day (n = 3), average of three concentrations of the formulation repeated three times within the same day.c The inter-day (n = 3), average of three concentrations of the formulation repeated three times in three successive days.
Intra-day precision and accuracy^b
2.00	98.33 ± 0.764	0.777	1.67	4.00	99.58 ± 0.878	0.882	0.417
10.00	99.30 ± 0.177	0.178	0.70	10.00	99.30 ± 1.609	1.621	0.700
16.00	99.77 ± 0.575	0.576	0.23	16.00	99.33 ± 0.781	0.786	0.667
Inter-day precision and accuracy^c
2.00	99.33 ± 2.081	2.095	0.667	4.00	98.50 ± 1.639	1.648	0.500
10.00	99.83 ± 0.672	0.673	0.167	10.00	99.03 ± 1.650	1.666	0.967
16.00	99.08 ± 0.840	0.847	0.917	16.00	99.06 ± 1.432	1.445	0.937

---

Similarly, the accuracy was assessed using the standard addition technique and via calculation of recovery, Table 9.

Table 9 Standard addition technique for determination of MD·HCl in pharmaceutical formulations

Midodrine® drops			Midodrine® tablets
Taken (μg mL^−1)	Added (μg mL^−1)	Recovery %	Taken (μg mL^−1)	Added (μg mL^−1)	Recovery %
a Mean of 3 determinations.
4.00	—		4.00	—
	2.00	98.90		2.00	98.90
	4.00	99.10		4.00	99.00
	6.00	98.80		6.00	99.80
	8.00	99.70		8.00	99.45
	10.00	98.79		10.00	99.00
	11.00	98.80		11.00	99.00
	13.00	98.40
Mean^a ± SD		98.90 ± 1.245			99.20 ± 0.355
n		7			6
RSD		0.400			0.358
Variance		0.159			0.126

---

3.4.3. Specificity. Method specificity was evaluated by applying the suggested technique on the corresponding pharmaceutical formulations (tablets and oral drops). The results shown in Table 9 confirm the absence of interference from common excipients and adjuvants usually co-formulated with the active ingredients.

All data were compared to a reference method.⁶ Table 10 shows that calculated t- and F-values are less than the hypothetical ones,²⁹ approving the absence of a significant difference between the compared approaches.

Table 10 Statistical data for the determination of MD·HCl using the proposed method compared with the reference method^a,6

Parameter	Proposed method	Comparison method^6
a Condensation with ninhydrin.b Mean of 3 determinations.c Values in parentheses indicate theoretical values of t and F at P = 0.05.
Mean^b ± SD	99.96 ± 0.659	100.00 ± 0.365
n	6	8
RSD	0.659	0.365
Variance	0.434	0.133
t-Test^c	0.134 (2.160)	—
F-Test^c	3.26 (3.97)	—

---

4. Conclusion

Spectrophotometric determination of MD·HCl was performed employing the Hantzsch reaction. With the purpose of minimizing the troubles associated with one-variable at time investigations (OVAT), and looking for a technique that saves time and cost; experimental design based on multivariable investigation was efficiently employed in the current paper. Factorial design was used to both investigate and optimize all the variables affecting the proposed reaction. For screening, a 2⁴-full factorial design (FFD) was used. For optimization, a response surface methodology (RSM) based on a face-centred central composite design was utilized. Both phases (screening and tuning) were statistically evaluated using ANOVA. Results obtained from all optimization procedures, either graphs (contour, response surface, analysis of residuals, and lack of fit), ANOVA testing, or desirability functions, infer that the developed model is adequate and can be used to detect the response without even performing the experiment. Method validation was performed following the ICH guidelines. Results obtained in terms of linearity, sensitivity, accuracy, and precision, further support the validity of the optimized procedure. The proposed method was successfully applied to midodrine formulations and results obtained were in good agreement with the label claim.

References

1. S. C. Sweetman, Martindale: The Extra Pharmacopeia-The Complete Drug Reference, Pharmaceutical Press, 2011.
2. R. A. Wright, H. C. Kaufmann, R. Perera, T. L. Opfer-Gehrking, M. A. McElligott, K. N. Sheng and P. A. Low, Neurology, 1998, 51, 120–124.
3. S. Prakash, A. X. Garg, A. P. Heidenheim and A. A. House, Nephrol., Dial., Transplant., 2004, 19, 2553–2558.
4. Anon, FDA, Midodrine update: opening of a public docket, http://www.fda.gov/Drugs/DrugSafety/PostmarketDrugSafetyInformationforPatientsandProviders/ucm239456.htm, on 11/01/2015.
5. O. AbdelSattar, M. R. Rezk, A. Badawy and O. M. Khattab, Anal. Chem.: Indian J., 2013, 12, 182–187.
6. A. El-Gindy, S. Sallam and R. A. Abdel-Salam, Anal. Chem.: Indian J., 2008, 7, 529–534.
7. R. Shahidha, A. A. Al-Saadi and S. Muthu, Spectrochim. Acta, Part A, 2015, 134, 127–142.
8. T. Barth, M. T. Pupo, K. B. Borges, L. T. Okano and P. S. Bonato, Electrophoresis, 2010, 31, 1521–1528.
9. T. Barth, J. Aleu, M. T. Pupo, P. S. Bonato and I. G. Collado, J. Chromatogr. Sci., 2013, 51, 460–467.
10. A. G. Fragkakia, M. A. Koupparisb and C. G. Georgakopoulos, Anal. Chim. Acta, 2004, 512, 165–171.
11. E. S. Elzanfaly, H. E. Zaazaa and H. A. Merey, Acta Chim. Slov., 2013, 60, 256–262.
12. F. R. S. D. Bratlon and W. D. Olis, Comprehensive Organic Chemistry, The Synthesis and Reactions of Organic Compounds, 4, Pergamon Press, London, 1979, vol. 65, p. 298.
13. N. N. Atia, A. M. Mahmoud, S. R. El-Shabouri and W. M. El-Koussi, Int. J. Anal. Chem., 2013, 2013, 1–11.
14. M. S. Elazazy, H. M. Khalil, M. N. Elbolkiny and A. Shalaby, Zagazig J. Pharm. Sci., 2004, 13, 6–11.
15. M. A. Korany, M. A. A. Ragab, R. M. Youssef and M. A. Afify, RSC Adv., 2015, 5, 6385–6394.
16. H. M. Saleh, M. M. El-Henawee, G. H. Ragab and O. F. Mohamed, Int. J. Pharm., Chem. Biol. Sci., 2014, 4, 738–747.
17. R. L. Plackett and J. P. Burman, Biometrika, 1946, 33, 302–325.
18. L. Timma, K. Sams, S. Valtere, J. Vilgerts and D. Blumberga, J. Clean Energy Technol., 2014, 2, 51–56.
19. L. V. Candioti, M. M. DeZan, M. S. Cámara and H. C. Goicoechea, Talanta, 2014, 124, 123–138.
20. M. A. Raji and K. A. Schug, Int. J. Mass Spectrom., 2009, 279, 100–106.
21. O. Abdel-Aziz, M. F. Ayad and M. M. Tadros, Spectrochim. Acta, Part A, 2015, 140, 229–232.
22. G. Derringer and R. Suich, J. Qual. Technol., 1980, 12, 214–219.
23. R. H. Myers, Response Surface Methodology: Process and Product Optimization Using Designed Experiments, John Wiley, Hoboken, 2009.
24. International Conference on Harmonization, ICH Harmonized Tripartite Guideline – Text on Validation of Analytical Procedures, Fed. Register, 1995, 60, 11260.
25. J. N. Miller and J. C. Miller, Statistics and Chemometrics for Analytical Chemistry, Prentice Hall/Pearson, 2010.
26. S. M. Khamanga and R. B. Walker, Talanta, 2011, 83, 1037–1049.
27. Y. Xiong, K. P. Xiao and A. M. Rustum, J. Pharm. Biomed. Anal., 2009, 49, 646.
28. J. S. Space, A. M. Opi, B. Nickerson, H. Jiang, M. Dumont and M. Berry, J. Pharm. Biomed. Anal., 2007, 44, 1064.
29. R. Caulcut and R. Boddy, Statistics for Analytical Chemists, Chapmann and Hall, London, 1983.

---

Footnote

† Permanent address: Analytical Chemistry Department, Faculty of Pharmacy, Zagazig University, Egypt.

---