Molecular dynamic simulations on the interaction between an HTPE polymer and energetic plasticizers in a solid propellant
Xiao-long Fu*a,
Xue-zhong Fana,
Xue-hai Jub,
Xiao-fei Qia,
JI-zhen Lia and
Hong-jian Yua
aXi'an Modern Chemistry Research Institute, Xi'an, 710065, China. E-mail: fuxiaolong204@163.com
bDepartment of Chemistry, Nanjing University of Science and Technology, Nanjing 210094, China
First published on 10th June 2015
Abstract
In order to study the interaction between a polymer and plasticizers in a solid propellant and their underlying mechanisms, molecular dynamics (MD) simulations with compass force fields were performed to investigate the Hydroxy Terminated PolyEther (HTPE) polymer and some energetic plasticizers including nitroglycerin (NG)/butanetriol trinitrate (BTTN) mixture, bis(2,2-dinitropropyl)acetal (BDNPA)/bis(2,2-dinitropropyl)formal (BDNPF) mixture and N-butyl-N-(2-nitroxy-ethyl)nitramine (Bu-NENA). Also, the mechanical properties for the HTPE polymer containing energetic plasticizers were theoretically and experimentally studied. It was shown that the HTPE polymer is miscible with all involved energetic plasticizers which can improve the mechanical property of the HTPE polymer. The order of binding energies between HTPE and the energetic plasticizers are found to be HTPE/Bu-NENA > HTPE/BDNPA/BDNPF > HTPE/NG/BTTN.
1. Introduction
Solid propellants are widely used in rockets and missiles.1–3 The ingredients of propellants mainly include polymers, plasticizers and energetic materials, etc.4–6 The polymer is an important ingredient for the improving mechanical properties of propellants, as well as reducing the sensitivity of propellants such as on impact or friction.7,8 HTPE propellants based on cross-linked Hydroxy Terminated PolyEther (HTPE) binders are widely studied as insensitive propellants.9,10 Although HTPE propellants have similar properties to HTPB propellants in most cases, the former ones are less sensitive.11,12 The mechanical properties of HTPE elastomers13,14 and HTPE propellants15 have been studied. However, there are no theoretical studies on interaction between an HTPE polymer and energetic plasticizers in propellants. In this work, the solubility parameter (δ), radial distribution function and binding energy of HTPE polymer with energetic plasticizers are theoretically studied by molecular dynamics (MD) simulations, and the mechanical properties for HTPE polymer containing energetic plasticizers are theoretically and experimentally studied. Hopefully, this study may provide some information and guidance for the design of HTPE propellants formulations.2. Model and method
2.1 Molecular model construction details
The molecular dynamic simulations were performed using the Accelrys and Materials studio Modeling (version 5.5) installed on Windows XP.16,17 The COMPASS Force Field was used for the molecular dynamic simulation on HTPE binder and the energetic plasticizers.18,19 The COMPASS has been proved as an effective force field supporting molecular simulations of polymer.20,21 The chemical structural of Hydroxy Terminated PolyEther (HTPE), nitroglycerin (NG), butanetriol trinitrate (BTTN), bis(2,2-dinitropropyl)acetal (BDNPA), bis(2,2-dinitropropyl)formal (BDNPF) and N-butyl-N-(2-nitroxy-ethyl)nitramine (Bu-NENA) were shown in Fig. 1. Here, carbon atoms are grey, hydrogen white, nitrogen blue and oxygen red in color. According to the force field, the H atoms in HTPE are assigned to H1; N atoms in nitro groups are N3O; O atoms in nitro groups are O1N; O atoms connected to nitro groups are OCN; O atoms connected to C chains in HTPE are O2E; O atoms connected to C chains in plasticizers are O2C; N atoms connected to nitro groups and C chains are N3.The molecular model of NG, BTTN, BDNPA, BDNPF and Bu-NENA were built with the Visualizer module in Materials studio software, and then their structures were optimized using Discover module. The HTPE polymer chains were built from repeat unit using the Random Copolymer Builder module whose molecular weight was 3000, and its structure was minimized (without an extensive conformer search) using Discover module.
2.2 Molecular dynamic simulation details
The HTPE/NG/BTTN, HTPE/BDNPA/BDNPF and HTPE/Bu-NENA blends were built by Amorphous cell, and the mass ratios were nearly 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25, 50
25, 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 and 50
25 and 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50. The size of the simulation box is 30 angstroms. The amorphous systems such as HTPE/NG/BTTN, HTPE/BDNPA/BDNPF and HTPE/Bu-NENA blends were subsequently optimized by a 5000 step energy minimization to eliminate the useless contacts by Smart minimization with convergence level of medium. Afterward, 400 ps MD equilibration on the system was performed to obtain the equilibrium density, with a time step of 1 fs, by Discover module in the NPT ensemble at 298 K and 101.325 kPa. The criterion for system equilibrium is the equilibrium of both temperature and the energy. The system of MD simulation is equilibrium when the fluctuation of temperature is within 10 K or the energy is invariable of small fluctuation around the average energy value. The molecular models of NG, BTTN, BDNPA, BDNPF, Bu-NENA, HTPE and their blends were shown in Fig. 2. The number of HTPE, plasticizers and mass ratios are summarized in Table 1.
50. The size of the simulation box is 30 angstroms. The amorphous systems such as HTPE/NG/BTTN, HTPE/BDNPA/BDNPF and HTPE/Bu-NENA blends were subsequently optimized by a 5000 step energy minimization to eliminate the useless contacts by Smart minimization with convergence level of medium. Afterward, 400 ps MD equilibration on the system was performed to obtain the equilibrium density, with a time step of 1 fs, by Discover module in the NPT ensemble at 298 K and 101.325 kPa. The criterion for system equilibrium is the equilibrium of both temperature and the energy. The system of MD simulation is equilibrium when the fluctuation of temperature is within 10 K or the energy is invariable of small fluctuation around the average energy value. The molecular models of NG, BTTN, BDNPA, BDNPF, Bu-NENA, HTPE and their blends were shown in Fig. 2. The number of HTPE, plasticizers and mass ratios are summarized in Table 1.
| System | Number of HTPE polymer chain | Number of plasticizers | Molecular ratio of HTPE and plasticizer |
|---|---|---|---|
| HTPE/NG/BTTN | 4 | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26 26 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 168 168 |
| HTPE/BDNPA/BDNPF | 4 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19 19 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 160 160 |
| HTPE/Bu-NENA | 4 | 58 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 006 006 |
2.3 Materials and formulations
Hydroxy Terminated PolyEther (HTPE, purity is over 99.8%, molecular weight is 3300), nitroglycerin (NG)/butanetriol trinitrate (BTTN) mixture (purity is over 99.7%), bis(2,2-dinitropropyl)acetal (BDNPA)/bis(2,2-dinitropropyl)formal (BDNPF) mixture (purity is over 99.8%) and N-butyl-N-(2-nitroxy-ethyl)nitramine (Bu-NENA, purity is over 99.6%). From the simulation of HTPE and plasticizer, the formulations of the three elastomers were designed as follows (Table 2):| Formulations | Mass percent/% | |||
|---|---|---|---|---|
| HTPE elastomer | NG/BTTN | BDNPA/BDNPF | Bu-NENA | |
| HE-1 | 50 | 50 | — | — |
| HE-2 | 50 | — | 50 | — |
| HE-3 | 50 | — | — | 50 |
2.4 Mechanical properties test
All the samples containing HTPE polymer and energetic plasticizer involved in this investigation were mixed for 30 min by stirrer. Then each sample was casted in a mold with 75 mm × 10 mm × 2 mm and cured at 50 °C for 3 days in a water jacketed oven.The mechanical properties of HTPE elastomers were measured by INSTRON 4505(USA) tensile tester. The elastomers were cut into slices with 75 mm × 4 mm × 2 mm, and the slices were made into JANNAF dog bones (Fig. 3). The tests were carried out at 25 °C with 500 mm min−1 cross-head speed.
3. Results and discussion
3.1 Solubility parameter
Miscibility is the property between polymer and plasticizer to mix in all proportions, forming a homogeneous solution.22 In order to predict the miscibility of the HTPE and energetic plasticizers, the solubility parameter can be calculated by MD method.23 In cohesive energy and cohesive energy density theories, the cohesive energy is used to estimate the energy change on mixing two species. When supplemented with the entropy of mixing this allows the prediction of the phase behavior of simple mixtures. These theories introduce the solubility parameter which can be used to predict solubility, particularly for non-polar materials such as polymers. Materials with similar solubility parameter values are likely to be miscible.The cohesive energy of a system of molecules, Ecoh, is the average energy required to separate all molecules to infinite distance from each other:
| Ecoh = −Einter = Eintra − Etotal | (1) |
The cohesive energy density, CED, is simply the cohesive energy per unit of volume:
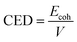 | (2) |
The solubility parameter, δ, is the square root of the cohesive energy density and plays an important role in the theory of mixtures:
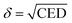 | (3) |
According to the theory of the polymer solution, the HTPE and energetic plasticizers including NG, BTTN, BDNPA and BDNPF blends can be considered as the polymer solution systems. The solubility parameters can be calculated by Material Studio according to the formula (1) to (3). Therefore, based on the dissolvable principle of similar material structures, when the solubility parameter of the plasticizer is close to the polymer, they can dissolve well with each other. The solubility parameters of HTPE and plasticizers are summarized in the Table 3.
| System | HTPE | NG/BTTN | BDNPA/BDNPF | Bu-NENA |
|---|---|---|---|---|
| a Note: ΔδMD is the differences of solubility parameters between HTPE and plasticizers. | ||||
| δMD/(J cm−3)0.5 | 19.034 | 21.106 | 19.886 | 19.687 |
| ΔδMD/(J cm−3)0.5 | — | 2.072 | 0.852 | 0.653 |
It is generally accepted that if |ΔδMD| < 1.3–2.1 (J cm−3)0.5 between polymers and plasticizers, the polymers and plasticizers would be expected miscible. This approach is only used to judge the miscibility of blends systems in which the non-combinatorial entropy effect or specific interactions do not play a dominant role. For our study, as shown in Table 3, ΔδMD of the energetic plasticizers are all less than 2.1 (J cm−3)0.5. The miscibility of HTPE and energetic plasticizers is good. The order of the compatibility of plasticizers with HTPE is Bu-NENA > BDNPA/BDNPF > NG/BTTN.
3.2 Simulation on mechanical properties of HTPE and energetic plasticizers
The simulation of mechanical properties is widely studied by MD method in energetic polymer system,24 amorphous polymer nanostructures25 and polymer liquid crystals.26Any body or element thereof, which is acted on by external forces is in a state of stress. Moreover, if the body is in equilibrium, the external stress must be exactly balanced by internal forces. In general, stress is a second rank tensor with nine components as follows. From the statistical mechanics of elasticity, the generalized Hooke's law is often written as formula (4).
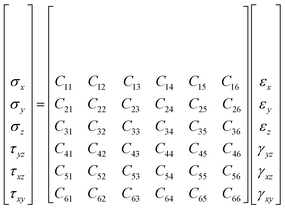 | (4) |
For isotropic body, there are only two independent elastic coefficients, C11 and C12. Let C12 = λ, C11–C12 = μ. Cij can be described as formula (5):
 | (5) |
In the formula, λ and μ are Lame constants. Tensile modulus (E), shear modulus (G), bulk modulus (K) and Poisson's ratio (ν) can be described as formula (6) to (9).
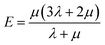 | (6) |
| G = μ | (7) |
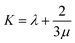 | (8) |
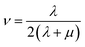 | (9) |
In an isotropic situation, where forces are the same in all directions and there is no viscous force, the pressure tensor is diagonal and can be written as:
 | (10) |
In materials science studies, the stress tensor is used in preference to the pressure tensor. The diagonal elements are known as the tensile stress and the non diagonal elements are the shear stress.
To obtain the theoretical elastic constants, the total energy of the bulk has been calculated for a number of deformations of the unit cell. The elastic constants of a crystal are defined as the second derivatives of energy density (at the energy minimum) with respect to the elements of the infinitesimal Lagrangian strain tensor εi, according to the relation:
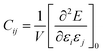 | (11) |
The mechanical properties can be calculated by MD simulation by formulae (5) to (11). The predicted value of elastic constants and effective isotropic mechanical properties are summarized in Table 4.
| Constants | HTPE | HTPE/NG/BTTN | HTPE/BDNPA/BDNPF | HTPE/Bu-NENA |
|---|---|---|---|---|
| C11/GPa | 0.344 | 2.592 | 2.103 | 1.283 |
| C22/GPa | −0.4612 | −4.93 | 3.939 | 2.252 |
| C33/GPa | 0.111 | −5.7 | 2.626 | 1.682 |
| C44/GPa | −1.933 | −2.08 | 1.017 | 1.099 |
| C55/GPa | 0.868 | −0.9362 | 1.29 | 0.564 |
| C66/GPa | 1.911 | −0.9591 | 0.6019 | 0.832 |
| C12/GPa | 1.191 | 1.444 | 1.279 | 1.177 |
| C13/GPa | −1.317 | 0.9082 | 0.9026 | 1.023 |
| C23/GPa | −2.212 | −2.269 | 1.736 | 0.862 |
| E/GPa | 2.720 | 2.415 | 2.392 | 2.083 |
| K/GPa | 1.709 | 1.5377 | 1.449 | 0.835 |
| G/GPa | 1.531 | 1.606 | 0.9304 | 0.828 |
| ν/GPa | 0.999 | 0.2485 | 0.2594 | 0.284 |
| C12–C44/GPa | 3.124 | 3.524 | 0.262 | 0.078 |
From Table 4, it can be found that elastic constants containing C11, C22 and C33 of HTPE/Bu-NENA and pure HTPE are closer than those of HTPE/NG/BTTN and HTPE/BDNPA/BDNPF. This evolution tendency of elastic constants showed that the Bu-NENA can reduce the anisotropy of HTPE than NG/BTTN and BDNPA/BDNPF. Moreover, compared with pure HTPE, all the mechanical properties including tensile modulus (E), shear modulus (G), and bulk modulus (K) of HTPE/plasticizers decrease. It indicates that the plasticizers can decrease the rigidity and increase the flexibility of HTPE. The mechanical property of HTPE can be improved by the energetic plasticizers.
3.3 Binding energy between HTPE and energetic plasticizers
The binding energy is a characteristic parameter which can represent the interaction force of components in composite system. The interaction energy can be evaluated by the total energy of the blends and each component in the system. The binding energies between HTPE polymer and energetic plasticizers can be determined using formula (12).| Ebinding = −Einter = −(EHTPE/plasticizer − EHTPE − Eplasticizer) | (12) |
In the formula, EHTPE/plasticizer is the total energy of HTPE and plasticizer blends system. EHTPE and Eplasticizer are the total energies of HTPE and plasticizer, respectively.
The binding energy between HTPE and energetic plasticizers were summarized in Table 5.
| System | EHTPE/plasticizer | EHTPE | Eplasticizer | Ebinding |
|---|---|---|---|---|
| HTPE/Bu-NENA | −2930.718 | 439.417 | −2260.919 | 1109.216 |
| HTPE/BDNPA/BDNPF | −2432.799 | 460.9426 | −1848.649 | 1045.0926 |
| HTPE/NG/BTTN | −1362.935 | 325.344 | −948.674 | 739.605 |
From Table 5, it is shown that the order of binding energy is HTPE/Bu-NENA > HTPE/BDNPA/BDNPF > HTPE/NG/BTTN. The interaction force between HPTE and Bu-NENA is stronger than those of BDNPA/BDNPF and NG/BTTN.
3.4 Radial distribution function for different atoms of HTPE and plasticizers
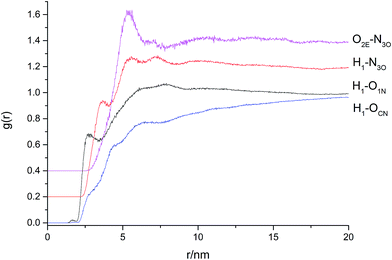
In order to reveal the interaction between the HTPE and plasticizers by atom function, the radial distribution functions are calculated. According to the studies, the distances of hydrogen bond and the van der Waals force are about 0.26 to 0.31 nm and 0.31 to 0.50 nm, respectively.27,28 Radial distribution functions (RDF) give the probability of finding another atom at a distance from a specific atom. The type of the interaction force can be judged by the distance of the peak in the radial distribution functions. The value of the force can be inferred by the height of the peak. The radial distribution functions of HTPE polymer and plasticizers were shown in Fig. 4 to 6.As shown in Fig. 4, there is a peak at about 0.26 nm which g(r) = 0.80 for the pair of H atoms in the terminal hydroxyl of HTPE and O atoms in nitro groups of the NG/BTTN (curve 5-1); the peak for the pair of H atoms in the terminal hydroxyl of HTPE and N atoms in nitro groups of the NG/BTTN is at about 0.34 nm which g(r) = 0.93 (curve 5-2); the RDF curve for the pair of H atoms in the terminal hydroxyl of HTPE and O atoms connected to nitro groups of the NG/BTTN has no peak (curve 5-3); there is a peak at about 0.49 nm which g(r) = 1.31 for the RDF curve for the pair of O atoms connected to C chains in HTPE and N atoms in nitro groups of the NG/BTTN (curve 5-4). From the RDF curves, the interaction force of H1–O1N is the hydrogen bond; there has no force between H1–OCN; the interaction forces of H1–N3O and O2E–N3O are van der Waals force. There is a main peak probably for strong interaction force between the pair of O atoms connected to C chains in the HTPE and N atoms in nitro groups of the NG/BTTN.
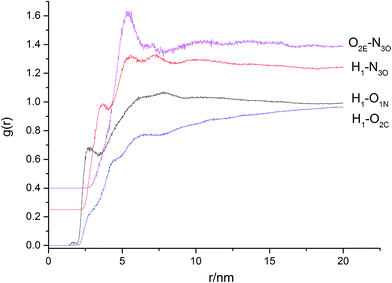
From the RDF curves, the interaction force of H1–O1N is the hydrogen bond; there has no force between H1–O2C; the interaction forces of H1–N3O and O2E–N3O are van der Waals force. There is a highest peak probably for strong interaction force between the pair of O atoms connected to C chains in the HTPE and N atoms in nitro groups of the BDNPA/BDNPF.
From the RDF curves, the interaction force of H1–O1N is the hydrogen bond; there has no force between H1–O2C; the interaction forces of H1–OCN, H1–N3O and O2E–N3O are van der Waals force. There is the highest peak for strong interaction force between the pair of O atoms connected to C chains in the HTPE and N atoms in nitro groups of the BDNPA/BDNPF.
It is concluded that the main interaction forces of HTPE and plasticizers are van der Waals force. The strong interaction forces are between the pair of O atoms connected to C chains in the HTPE and N atoms in nitro groups of the energetic plasticizers.
3.5 Mechanical properties of HTPE elastomers by experimental
In order to analyze the effects of plasticizers on the mechanical properties of HTPE elastomers, the maximum tensile strength (σm) and the maximum elongation (εm) of HTPE elastomers were listed in Table 6.| Formulations | Mechanical properties (25 °C) | |
|---|---|---|
| σm/(MPa) | εm/(%) | |
| HE-1 | 0.072 | 165.7 |
| HE-2 | 0.163 | 134.6 |
| HE-3 | 0.195 | 174.9 |
It was shown from Table 5 that the order of maximum tensile strength of HTPE elastomers is HE-3 > HE-2 > HE-1. From Fig. 7 it can be seen that there is nearly the same trend from the MD simulation and experiment. It can be inferred that the tensile strength might be the macro reflection of the molecular interaction. From the simulated of binding energy and radial distribution function that the mechanical property of HTPE polymer can be improved by energetic plasticizer due to the interaction force between the pair of O atoms connected to C chains in the HTPE and N atoms in nitro groups of the energetic plasticizers.
4. Conclusions
(1) It was found from calculations that the polymers and plasticizers were miscible and the order of the compatibility of plasticizers with HTPE is Bu-NENA > BDNPA/BDNPF > NG/BTTN.(2) MD simulations confirmed that the mechanical properties of the HTPE polymer can be improved by adding plasticizers; compared with pure HTPE, all the mechanical properties including tensile modulus (E), shear modulus (G), bulk modulus (K) of HTPE/plasticizers are greatly improved.
(3) The order of binding energy was theoretically found to be HTPE/Bu-NENA > HTPE/BDNPA/BDNPF > HTPE/NG/BTTN.
References and notes
- S. Asthana, C. Divekar and R. Khare, et al., Thermal Behaviour of AP Based CMDB Propellants with Stabilizers, Def. Sci. J., 2013, 42, 201–204 CrossRef.
- F. Doisneau, F. Laurent and A. Murrone, et al., Eulerian Multi-Fluid models for the simulation of dynamics and coalescence of particles in solid propellant combustion, J. Comput. Phys., 2013, 234, 230–262 CrossRef CAS PubMed.
- W. Nachbar, A theoretical study of the burning of a solid propellant sandwich, Solid Propellant Rocket Research, 2013, vol. 1, pp. 207–226 Search PubMed.
- Q. Zhang and J. M. Shreeve, Energetic Ionic Liquids as Explosives and Propellant Fuels: A New Journey of Ionic Liquid Chemistry, Chem. Rev., 2014, 114(20), 10527–10574 CrossRef CAS PubMed.
- F. Doisneau, J. Dupays and A. Murrone, et al., Eulerian versus Lagrangian simulation of unsteady two-way coupled coalescing two-phase flows in solid propellant combustion, C. R. Mec., 2013, 341, 44–54 CrossRef PubMed.
- B. S. Min, C. K. Kim and M. S. Ryoo, et al., Azide-bearing polymer-based solid composite propellant prepared by a dual curing system consisting of a urethane-forming reaction and a dipolar addition reaction, Fuel, 2014, 136, 165–171 CrossRef CAS PubMed.
- D.-H. Lee, K. T. Kim and H. Jung, et al., Characterization of 1,2,3-triazole crosslinked polymers based on azide chain-ends prepolymers and a dipolarophile curing agent as propellant binders: the effect of a plasticizer, J. Taiwan Inst. Chem. Eng., 2014, 45, 3110–3116 CrossRef CAS PubMed.
- H. Y. Zain-ul-Abdin, L. Wang and M. Saleem, et al., Synthesis, anti-migration and burning rate catalytic mechanism of ferrocene-based compounds, Appl. Organomet. Chem., 2014, 28(8), 567–575 CrossRef CAS PubMed.
- Z.-P. Huang, H.-Y. Nie and Y.-Y. Zhang, et al., Migration kinetics and mechanisms of plasticizers, stabilizers at interfaces of NEPE propellant/HTPB liner/EDPM insulation, J. Hazard. Mater., 2012, 229, 251–257 CrossRef PubMed.
- K.-H. Kim, C.-K. Kim and J.-C. Yoo, et al., Test-Based Thermal Decomposition Simulation of AP/HTPB and AP/HTPE Propellants, J. Propul. Power, 2011, 27, 822–827 CrossRef.
- H. Shen, Y. G. Yu and X. C. Xue, Study on Thermal Decomposition of AP/HTPB Base Bleed Propellant after Depressurization and Flameout Conditions, Adv. Mater. Res., 2013, 718, 191–195 CrossRef.
- T. D. Hedman, M. L. Gross and J. J. Davis, et al., Experimental Investigation of the Decomposition Preceding Cookoff in a Composite Propellant, J. Propul. Power, 2014, 30, 1–8 CrossRef.
- C.-D. Wang, Y.-J. Luo and M. Xia, Synthesis of HTPE and Properties of HTPE Elastomers, Chin. J. Energ. Mater., 2011, 5, 012 Search PubMed.
- K.-Z. Mao, M. Xia and Y.-J. Luo, et al., Effect of Curing Agent Types on Properties of HTPE Polyurethane Elastomer Films, Chin. J. Explos. Propellants, 2012, 1, 012 Search PubMed.
- C.-D. Wang, Y.-J. Luo and M. Xia, et al., Synthesis and characterization of hydroxyl-terminated block copolyether of PTHF-PEO-PTHF, J. Solid Rocket Technol., 2011, 2, 017 Search PubMed.
- Y. Z. Fu, L. Q. Liao and L. X. Yang, et al., Molecular dynamics and dissipative particle dynamics simulations for prediction of miscibility in polyethylene terephthalate/polylactide blends, Mol. Simul., 2013, 39, 415–422 CrossRef CAS PubMed.
- M. Rahmati, H. Modarress and R. Gooya, Molecular simulation study of polyurethane membranes, Polymer, 2012, 53, 1939–1950 CrossRef CAS PubMed.
- S. S. Jawalkar, K. V. Raju and S. B. Halligudi, et al., Molecular modeling simulations to predict compatibility of poly(vinyl alcohol) and chitosan blends: a comparison with experiments, J. Phys. Chem. B, 2007, 111, 2431–2439 CrossRef CAS PubMed.
- K.-L. Tung, K.-T. Lu and R.-C. Ruaan, et al., Molecular dynamics study of the effect of solvent types on the dynamic properties of polymer chains in solution, Desalination, 2006, 192, 380–390 CrossRef CAS PubMed.
- S. S. Jawalkar and T. M. Aminabhavi, Molecular modeling simulations and thermodynamic approaches to investigate compatibility/incompatibility of poly(L-lactide) and poly(vinyl alcohol) blends, Polymer, 2006, 47, 8061–8071 CrossRef CAS PubMed.
- B. Derecskei and A. Derecskei-Kovacs, Molecular dynamic studies of the compatibility of some cellulose derivatives with selected ionic liquids, Mol. Simul., 2006, 32, 109–115 CrossRef CAS PubMed.
- S. S. Jawalkar, S. G. Adoor and M. Sairam, et al., Molecular modeling on the binary blend compatibility of poly(vinyl alcohol) and poly(methyl methacrylate): an atomistic simulation and thermodynamic approach, J. Phys. Chem. B, 2005, 109, 15611–15620 CrossRef CAS PubMed.
- J. L. Lewin, K. A. Maerzke and N. E. Schultz, et al., Prediction of Hildebrand solubility parameters of acrylate and methacrylate monomers and their mixtures by molecular simulation, J. Appl. Polym. Sci., 2010, 116, 1–9 CrossRef CAS PubMed.
- X. F. Ma, J. J. Xiao and H. Huang, et al., Effects of concentration and temperature on mechanical properties of TATB/PCTFE pbx by molecular dynamics simulation, Chin. J. Chem., 2005, 22, 2037–2041 Search PubMed.
- D. Qi, J. Hinkley and G. He, Molecular Dynamics Simulation of Thermal and Mechanical Properties of Polyimide-Carbon-Nanotube Composites, Modell. Simul. Mater. Sci. Eng., 2005, 4, 493–507 CrossRef.
- A. I. Melker and A. N. Efleev, Computer simulation of structure and mechanical properties of polymer liquid crystals, J. Macromol. Sci., Part B: Phys., 1999, 38(5), 769–785 CrossRef PubMed.
- J. R. Durig, K. W. Ng and Z. Chao, et al., Comparison of Ab Initio MP2/6-311+G(d,p) Predicted Carbon–Hydrogen Bond Distances with Experimentally Determined r0 (C–H) Distances, Struct. Chem., 2004, 15(2), 149–157 CrossRef CAS.
- T. Steiner and G. R. Desiraju, Distinction between the weak hydrogen bond and the van der Waals interaction, Chem. Commun., 1998, 891–892 RSC.
| This journal is © The Royal Society of Chemistry 2015 |