Rheological behavior of hydrophobically modified polysulfobetaine methacrylate aqueous solution

Abstract

Polysulfobetaine methacrylate (PSBMA) that was hydrophobically modified with methacrylic acid 2,3-epoxypropyl ester (GMA) was synthesized via the micellar copolymerization method. Basic properties of the obtained copolymer were investigated via fluorescence, transmission electron microscopy (TEM), dynamic light scattering (DLS), zeta-potential analyzer, etc. The rheological properties of polymer (or copolymer) solutions were determined as a function of shear rate, temperature, NaCl concentration, etc. Hydrophobically modified PSBMA were capable of forming micelles even at extremely low concentrations (0.001 g L⁻¹), and the micelle sizes increased upon increasing concentration. Hydrophobic interactions were observed within the system and were enhanced with increasing copolymer concentration. Both PSBMA with and without hydrophobic modification exhibited negative zeta-potential and increased with increasing polymer concentration. The viscosity of the P(SBMA–GMA) aqueous solution showed features that are different from those of typical polymer solutions. In addition, the rheological behavior of hydrophobically modified PSBMA aqueous solution had an unusual relationship with temperature because of hydrophobic association and epoxy groups. The viscosity of hydrophobically modified PSBMA solution was sensitive to the added salt concentration, i.e., the viscosity initially decreased and subsequently increased upon the addition of salt.

---

1 Introduction

Recently, studies have focused on polyzwitterionic compounds, including poly[2-methacryloyloxethyl phosphorylcholine (MPC)],^1–3 polycarboxybetaine methacrylate (CBMA),⁴ and polysulfobetaine methacrylate (SBMA),⁵ because of their ultra-low-fouling property. Surfaces that are coated with these polymers allow for a nonspecific protein adsorption of up to 5 ng cm⁻², which can effectively inhibit platelet adhesion for blood compatibility.⁶ The ultra-low-fouling property of polyzwitterionic materials is caused by the high hydration around the opposing charges and the high energetics required to remove that hydration layer.⁷ Therefore, polyzwitterionic compounds were reported to have considerable potential in many applications, such as medical implants,⁸ marine coatings,⁹ and biosensors.¹⁰

In recent years, despite the excellent antifouling property of polyzwitterionic compounds, many scholars focused on solution properties, both theoretically^11–15 and experimentally.^16,17 The unique properties of polymeric betaines are strongly related to the opposite charge interactions in aqueous solutions.^18,19 The states of polyzwitterionic chain can be varied by adjusting the temperature,^20–22 pH value,^23,24 salt concentration and so on.^22,25 Dobry and Rubinstein developed the Flory theory of polyampholyte, and they proposed a two-parameter theoretical model that can forecast and explain several polyampholyte properties precisely.²⁶

Hydrophobically associating polymers contain a small proportion of hydrophobic groups that are incorporated in a hydrophilic polymer chain (usually as pendant side chains or terminal groups). In aqueous solution, beyond a specific polymer concentration, a transitory three-dimensional network of polymer chains is formed as a result of the intermolecular interactions of the hydrophobic group.²⁷ These compounds are used in many applications, such as water-borne coatings, paints, cosmetics, and enhanced oil recovery.^28–30 From a technological perspective, the rheological behavior of these associative polymers is a highly significant feature. Hill and his coworkers^31,32 investigated the system of hydrophobically associating polyacrylamides. They proposed a mechanism of this synthetic method and stated that the microstructure can be adjusted by varying the hydrophobe/surfactant ratio, i.e., the number of hydrophobes per micelle.³¹ Meanwhile, several researchers have found that these polymers have unique rheological behaviors.^33–35 However, to our best knowledge, few studies have focused on the rheological behavior of polyzwitterionic compounds that are modified by hydrophobic monomers.^36,37 With more and more application of polyzwitterionic compounds in a solution mode, it is necessary to explore the corresponding rheological behavior.

In the present paper, hydrophobic monomers are introduced into the polyzwitterionic chain backbones via the micellar copolymerization method.³¹ The aggregation properties of associative polymers are characterized via fluorescence measurement, and the morphology of these hydrophobically associating polymers are observed via transmission electron microscopy (TEM). Subsequently, the effects of concentration (c), salt addition, and temperature on the rheological behavior of hydrophobically modified polyzwitterionic compound aqueous solution are also discussed.

2 Experimental section

2.1 Materials

N-(3-Sulfopropyl)-N-(methacryloxyethyl)-N,N-dimethylammonium betain (SBMA) was purchased from Sigma-Aldrich. Methacrylic acid 2,3-epoxypropyl ester (GMA) was purchased from Aladdin. Tween 20 was purchased from Wenzhou Qingming Chemical Co., Ltd. 2,2′-Azobis[2-(2-imidazolin-2-yl) propane] dihydrochloride (VA-044) was purchased from J&K Scientific Ltd. The water used for all experiments was ultrapure and supplied by a water purification system. All of the other reagents were used without further purification.

2.2 Synthesis of SBMA–GMA copolymer

SBMA–GMA copolymer [P(SBMA–GMA)] was synthesized via micellar copolymerization^31,32 in 1 mol L⁻¹ NaCl aqueous solution, and VA-044 was used as the initiator. The reaction vessel was a four-necked flask equipped with a condenser tube, mechanical stirrer, thermometer, and nitrogen inlet/outlet. Tween 20, which functions as an emulsifier, and GMA were first dissolved in 1 mol L⁻¹ NaCl solution (40 mL) and were then transferred into the flask with stirring. After 0.5 h, SBMA dissolved in 1 mol L⁻¹ NaCl solution (50 mL) was poured into the flask. The mass ratio of SBMA to GMA is 10 : 1. The mixture was stirred in an inert nitrogen atmosphere and heated at 50 °C in an oil bath. After 0.5 h, VA-044 dissolved in 1 mol L⁻¹ NaCl solution (10 mL) was injected using a syringe. The reaction proceeded for 7 h. After cooling the final reaction mixture, the copolymer was precipitated by dropwise addition into excess ethanol, and subsequent dissolution–precipitation for three times. The final precipitate obtained was put in a Petri dish and then was stored in a refrigerator at −30 °C for about 24 h. After completely frozen, the sample was then transferred it into a vacuum freeze drier (FD-1-50, Beijing Boyikang Laboratory Instruments Co., Ltd) at −51 °C, 15 Pa for 12 h. At last, the dry product was obtained. In contrast with the copolymer, homopolymer PSBMA was synthesized using the same conditions.

Molecular weights (M_w) and distributions of P(SBMA–GMA) and PSBMA were characterized via gel-permeation chromatography (GPC) measurements at 25 °C. The eluent was 0.1 mol L⁻¹ NaNO₃, with a flow rate of 0.8 mL min⁻¹. The results are shown in Table 1. The mass percentage of the GMA monomer in the copolymer was approximately 9%.

Table 1 Molecular weight and distribution of PSBMA and P(SBMA–GMA)

Sample	Mw (g mol^−1)	Polydispersity index
PSBMA	1.1416 × 10^4	1.32
P(SBMA–GMA)	13.6179 × 10^4	1.12

---

2.3 Fluorescence measurement

Before adding the polymer solution, a sufficient amount of pyrene solution, which was first dissolved in methanol, was evaporated in 10 mL volumetric flasks under a nitrogen stream. The resulting pyrene concentration was 5 × 10⁻⁷ mol L⁻¹ after adding the polymer solution.³² The mixed solutions were allowed to equilibrate for 24 h with shaking prior to fluorescence runs. Then the sample was scanned for emission spectra (λ_ex = 335 nm), which was obtained by averaging three scans, and corrected for scatter using equivalent blank polymer sample. Steady-state fluorescence measurements were performed on a Pekin-Elmer LS-55 FL spectrofluorometer at 25 °C with an excitation wavelength of 334 nm.

2.4 TEM measurement

The morphologies of association micelles in the aqueous solution were observed using a JEOLIEM-1200 TEM instrument with an accelerating voltage of 60 kV. The samples were placed on copper grids coated with films at different concentrations. After the solvent completely evaporated, the measurement was carried out.

2.5 Dynamic light scattering (DLS) and static light scattering (SLS) measurement

All the solutions used in DLS and SLS measurements were prepared by dissolving different amounts of P(SBMA–GMA) copolymer in 1 mol L⁻¹ NaCl aqueous solution. After stirring for three days, all solutions were filtered through Millipore 0.45 μm membranes and were then transferred into special bottles for DLS or SLS measurement. Subsequently, the experiments were carried out using a Brook-haven instrument (USA).

2.6 Zeta-potential measurement

The zeta-potential ζ, which is a parameter used to study electrostatic interactions, was measured using a Zetasizer Nano Series (Malvern) for a series of polymer solutions with different NaCl concentrations.

2.7 Rheological test

All rheological measurements were performed using an AR-G2 rheometer (TA Instruments, USA), a stainless steel cone (40 mm diameter, 2°) and a plate. For the rheological test, the solutions were prepared by stirring for at least 24 h to obtain apparent homogeneity. The strain was set to 2% for frequency sweep tests in the linear viscoelastic region of the copolymer and homopolymer aqueous solutions.

3 Results and discussion

3.1 Fluorescence characteristics

Complementary fluorescence techniques have been widely applied to explore the aggregate properties of associative polymers.^38,39 Usually, five emission peaks in the fluorescence spectra are at the 373, 379, 384, 394, and 480 nm. The intensity ratio (I₁/I₃) of the first peak (I₁) to the third peak (I₃) is sensitive to hydrophobic environment.^32,40 The highest value of I₁/I₃ is approximately 1.87 in water, and this value decreases in a hydrophobic environment.⁴⁰ The decrease in I₁/I₃ relative to pure water (without polymer) reflects the slight hydrophobicity of the polymeric backbone despite the presence of hydrophilic ionic sites.³⁹ Fig. 1 presents the variation in I₁/I₃ as a function of P(SBMA–GMA) concentration (c_{P(SBMA–GMA)}) in water. The curve shows the characteristic sigmoidal shape of three regions. When c_{P(SBMA–GMA)} is very low, pyrene senses the hydrophilic surrounding, I₁/I₃ approaches the value recorded in the pure solvent. At a specific c_{P(SBMA–GMA)}, I₁/I₃ starts to decrease, and the decline is not as steep as that observed in the case of surfactant solutions because the range of the two-order magnitudes also change with concentration. This behavior reflects the pyrene partition between the aqueous phase and the hydrophobic domains, which indicates that hydrophobic interactions exist in the P(SBMA–GMA) aqueous solution. These interactions are enhanced with increasing c_{P(SBMA–GMA)}.

Fig. 1 Fluorescence intensity ratio I₁/I₃ of pyrene probe as a function of c_{P(SBMA–GMA)} at an excitation wavelength of 334 nm.

3.2 P(SBMA–GMA) morphology in aqueous solution

The morphology of P(SBMA–GMA) in aqueous solution with different c_{P(SBMA–GMA)} values were observed via TEM (Fig. 2). From Fig. 2, the P(SBMA–GMA) macromolecular chains form micelles at both extremely low (0.001 g L⁻¹) and high concentrations (1 g L⁻¹), in which the average micelle diameters increase with increasing c_{P(SBMA–GMA)}. The aggregation of hydrophobic blocks (GMA) is believed to cause the formation of these micelles with the hydrophilic blocks (PSBMA) as the shell.⁴¹ The micelle sizes in 1 g L⁻¹ (Fig. 2(c)) are only a little larger than that of 0.01 g L⁻¹ (Fig. 2(b)). However, the micelles with larger sizes are dominant in the case of 1 g L⁻¹.

Fig. 2 Morphology of P(SBMA–GMA) in an aqueous solution at different concentrations: (a) 0.001; (b) 0.01; (c) 1 g L⁻¹.

For most polyelectrolytes with a hydrophobic backbone, the electrostatic repulsion, whether weak or strong, favors chain stretching. Increasing the amount of salts generally results in repulsion screening and eventually provokes the collapse,⁴² and sometimes, the precipitation of the backbone. On the contrary, Coulombic attraction between ammonium and sulfonate groups of opposite charges along the polymer backbone hinders the dissolution of polyzwitterions in water. Coulombic attraction may be inter- or intramolecular, which results in an attraction between ammonium and sulfonate of the same or different monomers or polymer chains.⁴³ Salts that are added in the solution may screen this kind of attraction. However, polyzwitterions, which bear both charges on the same monomeric unit and are thus virtually neutral, should not be highly sensitive to salt concentration compared with negatively and positively charged polyelectrolytes. Nevertheless, the solubility of P(SBMA–GMA) increases in NaCl aqueous solution. Even so, P(SBMA–GMA) still forms micelles in NaCl aqueous solution because of the introduction of hydrophobic blocks.⁴⁴ In addition, the TEM image of P(SBMA–GMA) in NaCl aqueous solution can not be obtained because of the formation of NaCl crystals when water is evaporated. Fig. 3 presents the P(SBMA–GMA) micelle diameters in 1 mol L⁻¹ NaCl aqueous solutions obtained via DLS. At c_{P(SBMA–GMA)} = 0.01 g L⁻¹, the micelle diameters are from 20 nm to 700 nm. At c_{P(SBMA–GMA)} = 1 g L⁻¹, the sizes vary from 20 nm to 400 nm, which have a relatively narrower diameter distribution than that in the case of c_{P(SBMA–GMA)} = 0.01 g L⁻¹. It is noted that both of the samples exhibit bimodal distributions. In the dissolution process, the hydrophobic sections are associated together, and the hydrophilic sections should be outside the micelles.⁴² However, as both of the samples are in dilute solution regime (which can be proved by Fig. 6), micelles with different sizes can't overlap with each other. Therefore, the smaller micelles are those with a relatively small amount of hydrophobic association, which may be primarily the intramolecular associations, and the bigger ones are those with a large amount of hydrophobic associations, which may contain both the intra- and intermolecular associations.⁴⁵

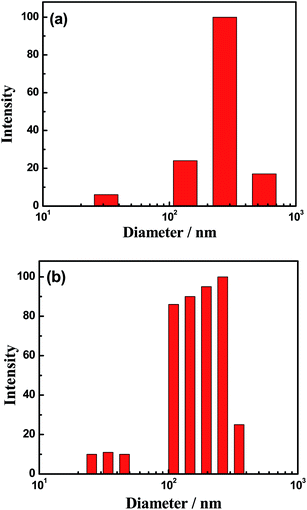Fig. 3 Distribution of P(SBMA–GMA) micelles in an NaCl aqueous solution (NaCl concentration is 50 g L⁻¹) at different copolymer concentrations at 25 °C: (a) 0.01 and (b) 0.1 g L⁻¹.

3.3 Zeta-potential measurement

Fig. 4 shows the PSBMA and P(SBMA–GMA) zeta-potential (ζ) data in various NaCl aqueous solutions (c_NaCl). PSBMA has an apparent negative zeta-potential (ζ_PSBMA) of −25.16 mV in water. P(SBMA–GMA) also has an apparent negative zeta-potential (ζ_{P(SBMA–GMA)}) of −23.6 mV in water, which is slightly higher than that of PSBMA because of the introduction of GMA. This result is in fact a general feature since all salt-free polysulfobetaine had negative zeta-potentials.²² From Fig. 5, ζ_PSBMA and ζ_{P(SBMA–GMA)} increase with increasing c_NaCl. The result implies that Na⁺ interacts very strongly with –SO₃⁻ than Cl⁻ does with (CH₃)N⁺.^43,46 Based from the research conducted by Mary, the apparent negative zeta-potential is probably consistent with the partial hydrolysis of acrylic acid functional groups.²² The preferential complexation of SBMA segment with Na⁺ results in an increased zeta-potential because the positive charge of Na⁺ compensates for the net anionic charge of partially hydrolyzed SBMA units. In other words, the sulfonated sites can have a stronger interaction with the added cation than the interaction between quaternized ammonium sites and the anions. In addition, the net negative charges significantly promote the P(SBMA–GMA) and PSBMA solubilities because of the repulsive contribution among uncompensated negative charges.¹² Compared with pure PSBMA, the introduction of GMA results in an insignificant change in response to c_NaCl.

Fig. 4 Zeta-potential as a function of the NaCl salt concentration measured on PSBMA and P(SBMA–GMA) solutions at a constant polymer concentration of 20 g L⁻¹.

Fig. 5 Shear rate dependence of the apparent viscosity of different P(SBMA–GMA) aqueous solution concentrations at 25 °C.

3.4 Rheological behaviors

Viscoelastic behaviors are strongly influenced by hydrophobic association.³¹ In the present paper, the rheological behavior of PSBMA and P(SBMA–GMA) aqueous solution with different concentrations were investigated. As mentioned above, the P(SBMA–GMA) aqueous solution is actually a heterogeneous system due to hydrophobic block aggregation. Fig. 5 shows the apparent viscosity (η_a) versus shear rate ([small gamma, Greek, dot above]) for P(SBMA–GMA) aqueous solution with various c_{P(SBMA–GMA)}. For P(SBMA–GMA) solutions with a high concentration, obvious shear-thinning was observed with increasing [small gamma, Greek, dot above]. No shear-thickening behavior was observed presumably because of low M_w and low hydrophobic block content (∼9%), which is different from other hydrophobically associating polyampholytes systems.^47,48

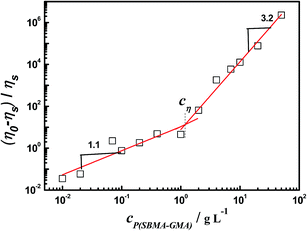
The specific viscosity (η_sp) of P(SBMA–GMA) aqueous solution with various c_{P(SBMA–GMA)} was obtained using the equation η_sp = (η₀ − η_s)/η_s, where η₀ is the zero-shear viscosity and η_s is the solvent viscosity (i.e., water). In the case of high c_{P(SBMA–GMA)}, η_a at [small gamma, Greek, dot above] of 10⁻³ s⁻¹ is considered as zero-shear viscosity because no η₀ is observed even if [small gamma, Greek, dot above] is as low as 10⁻³ s⁻¹. The variations of η_sp as a function of c_{P(SBMA–GMA)} plot in water are shown in Fig. 6. η_sp increases slightly at low c_{P(SBMA–GMA)} and rises steeply beyond a critical concentration, c_η. The crossover between the two regions is well defined, c_η ≈ 1.1 g L⁻¹. At c_{P(SBMA–GMA)} < c_η, η_sp ∝ c^1.1, while η_sp ∝ c^3.2 at c_{P(SBMA–GMA)} > c_η. These two regions are then considered to be dilute solution and semidilute solution respectively. Different from the polymer coils in typical neutral polymer dilute solution, there are some isolated micelles formed by intra- and intermolecular associations in dilute P(SBMA–GMA) aqueous solution as shown in Fig. 2. Some other groups found the crossover concentration between the dilute and the semidilute regime is most of the time equivalent to the critical overlap concentration (c*), meanwhile, the scales of viscosity versus concentration of the modified and unmodified polymer in dilute regime are similar.^49,50 Colby's result shows that for both the polyelectrolyte and neutral polymer solutions in dilute regime, η_sp ∝ c^1.0 can be found,⁵¹ which is approximately consistent with Fig. 6. At semidilute solution, most of these associative aggregate micelles can overlap with each other, and the viscosity increase sharply with concentration.⁵² It is hard to differentiate the semidilute unentangled regime and semidilute entangled regime in the present case. What we can infer is that the hydrophobic aggregation leads to the formation of micelles that grow with increasing concentration until at a critical concentration they percolate into a space spanning transient network.^49,53

Fig. 6 Specific viscosity of P(SBMA–GMA) aqueous solution with various concentrations at 25 °C.

In addition, it is noted that shear thinning is observed even at c_{P(SBMA–GMA)} < 1.1 g L⁻¹, which is quite different from typical dilute polymer solutions. From Fig. 2 we know that the micelles with different sizes have already formed in dilute regime. Micelles with large sizes would suffer shearing and lead to the viscosity decrease with increasing shear rate.

Fig. 7 shows the dynamic rheological behavior of PSBMA and P(SBMA–GMA) aqueous solution at 100 g L⁻¹. From Fig. 7(a), the storage (G′) and loss moduli (G′′) increase with increasing test frequency (ω) for both solutions, which is consistent with those obtained from common polymer solutions. The PSBMA aqueous solution at 100 g L⁻¹ concentration has a higher G′′ than G′ over the test ω range. However, G′ is dominant over G′′ for the P(SBMA–GMA) aqueous solution in the test ω process despite having the same concentration as PSBMA, and the solution behaves like a weak gel. The hydrophobic association of GMA blocks is believed to enhance the interaction between the micelles and then favor the weak-gel formation.⁴⁸ Another technique to confirm the formation of weak gels is to focus on the phase angle (δ) and by applying the formula tan δ = G′′/G′. When δ ≤ 45°, the samples behave like a gel. By contrast, the samples maintain a solution state at δ > 45°.⁴⁸ As shown in Fig. 7(b), δ of P(SBMA–GMA) is about 10° and remains constant over the test ω scope; however, δ of PSBMA has a high value and only exhibits a value lower than 45° at high ω.

Fig. 7 (a) Frequency dependence of the storage (G′) and loss moduli (G′′) of the P(SBMA–GMA) and PSBMA solutions at 100 g L⁻¹. (b) Phase angle δ as a function of frequency for the same data.

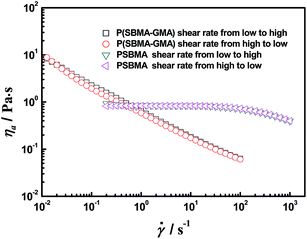
Another interesting feature that was investigated involves the reversibility of the rheological measurement during increasing and decreasing shear process. For PSBMA, the samples exhibit a classical rheological behavior, i.e., the viscosity is maintained constant at relatively low [small gamma, Greek, dot above],²⁷ and subsequent shear thinning at [small gamma, Greek, dot above] > 10² s⁻¹ occurs. The curves obtained during increasing and decreasing ramps are fully superimposed with each other (Fig. 8). The P(SBMA–GMA) copolymer solutions, which were prepared via micellar copolymerization, behave differently. Shear thinning occurs pronouncedly even at extremely low [small gamma, Greek, dot above]. It is noted that the P(SBMA–GMA) aqueous solution curves obtained during increasing and decreasing ramps are also fully superimposed with each other, which is similar to that of PSBMA aqueous solution. Such viscosity decrease and recovery phenomena are usually related to the disentangling and re-entangling of polymer chains, however, it may be different for P(SBMA–GMA) aqueous solution. The recovery in viscosity for the P(SBMA–GMA) aqueous solution during decreasing [small gamma, Greek, dot above] ramp test is perhaps caused by P(SBMA–GMA) large associative micelles re-entangling. And the disentangling among micelles, rather than the destruction of little hydrophobic aggregates, cause shear thinning at low [small gamma, Greek, dot above] for the P(SBMA–GMA) solution during increasing [small gamma, Greek, dot above] ramp test. Based on the SLS results, the micelle gyration radius, R_g, of a micelle formed by a P(SBMA–GMA) chain is 97 nm. The characteristic relaxation time, τ, then can be estimated using the equation τ ≅ η_sR_g³/kT, where k is the Boltzmann constant and T is the absolute temperature. For a micelle formed by a P(SBMA–GMA), τ is about 2.4 × 10⁻⁴ s. The critical shear rate for such micelle is 4.2 × 10³ s⁻¹. The maximum shear rate measured by a rheometer is only 1 × 10³ s⁻¹. Therefore, shear could only result in the transformation of large micelles to increasingly smaller ones through disentangling. However, this process could not destroy the little hydrophobic aggregates, which requires a relatively longer recovery time.⁵⁴

Fig. 8 Apparent viscosity as a function of shear rate for copolymer and homopolymer solutions at 25 °C at a concentration of 50 g L⁻¹.

The effect of temperature on the rheological behavior of hydrophobic association polymers is significant for applications. Fig. 9 shows the temperature dependence of viscosity for copolymer and homopolymer aqueous solutions. For PSBMA, the viscosity decreases with gradual increases in temperature and increase with decreasing temperature. Note that the data from the procedure are in accordance with those obtained using a conventional neutral polymer solution temperature ramp procedure.⁵⁵ The Arrhenius equation can be used to depict temperature dependence of the PSBMA aqueous solution viscosity, as shown in Fig. 9(a). The Arrhenius equation is stated as,

η = A e^ΔE_η/RT (1)

where A is a constant parameter, ΔE_η is the flow activation energy for the system, and R is the molar gas constant (8.31 J mol⁻¹ K⁻¹). The ΔE_η of PSBMA is 32.45 kJ mol⁻¹. Compared with other polyelectrolytes, such as dissociative PAA (where ΔE_η is approximately 8.4 kJ mol⁻¹),⁵⁵ the viscosity of the PSBMA aqueous solution is much more sensitive to temperature. However, the viscosity of P(SBMA–GMA) slightly increases with increasing temperature and is nearly maintained constant with decreasing temperature. Increasing the temperature improves the molecular thermal motion, which decreases the solution viscosity. On the contrary, several authors have claimed that increasing the temperature favors hydrophobic associations^56–58 and causes the viscosity to increase. In the present case, the net result of the two opposite effects in the heating process causes the viscosity to increase. More importantly, the GMA epoxy groups open if the temperature is higher than 60 °C, which leads to gel formation with the network structure. As a result, the viscosity of the solution increases. When temperature decreases, the hydrophobic association also decreases; however, the molecular thermal motion is restrained. Simultaneously, the network structure formed by the epoxy groups is maintained when the temperature is decreased. Therefore, the viscosity maintains a constant value during the cooling process. Fig. 9(b) shows the temperature dependence of G′ and G′′ of the P(SBMA–GMA) aqueous solution. G′ slightly decreases and then increases during the heating process; whereas in the cooling process, G′ increases. However, G′′ is almost kept slightly changed during the whole process. Therefore, G′ is much more sensitive to temperature than G′′ because network structures are formed during the heating process.

Fig. 9 (a) Temperature dependence of apparent viscosity for P(SBMA–GMA) and PSBMA at a shear rate of 0.01 s⁻¹ at 100 g L⁻¹. (b) Temperature dependence of G′ and G′′ at a frequency of 0.1 Hz for P(SBMA–GMA).

Many research have focused on the salt concentration dependence of viscosity for polyampholyte solutions.^59,60 Several researchers have pointed out that salt ions could affect the chain conformations to screen the repulsion between excess charges and the attraction between opposite charges.^12,26 Schulz found that polysulfobetaine solutions display an antipolyelectrolyte behavior, i.e., viscosities that increase with increasing salt concentrations.⁶¹ In the current study, the relationship between salt concentration and the viscosity of hydrophobically modified PSBMA solution is shown in Fig. 10. The viscosity initially decreases and then increases when more salt was added. A critical point in the curves is observed. To explain this phenomenon, we recourse to the theory proposed by Mary.²² The Debye length l_D is defined as,⁶²

l_D = 0.3/[NaCl]^1/2 (2)

where the concentration units [NaCl] are in moles per liter (M). l_D at different NaCl concentrations are shown in Table 2. According to Mary, the average microscopic distance l_D± between ammonium and sulfonate charges, which are confined inside a polyzwitterionic coil, is defined as,²²

l_D± = (4a³N^1/2)^1/3 (3)

where a is the characteristic SBMA monomer size, a is equal to 0.69 nm, and N is the degree of polymerization. For P(SBMA–GMA), N represents the SBMA monomer quantity that was polymerized from the copolymer. The critical NaCl salt concentration (c_±) can be calculated as follows:²²

c_± ≈ (3/2πa³)N^1−3β (4)

Fig. 10 NaCl salt concentration dependence of viscosity for P(SBMA–GMA) at a shear rate of 0.1 s⁻¹ at 20 g L⁻¹ and 25 °C.

Table 2 Debye length (l_D) at various NaCl concentrations

cNaCl (g L^−1)	0	0.1	1	10	100
lD (nm)	—	7.25	2.29	0.72	0.23

---

According to Mary, β is the power exponent associated with the solvent quality for the polymer chain. In the current study, β should be equal to 1/2. For P(SBMA–GMA) copolymers, M_w = 1.4 × 10⁵; therefore, N is approximately equal to 400. We can then estimate c_± is to be approximately 0.08 mol L⁻¹. This value is almost consistent with the experimental data at 1 g L⁻¹, which is approximately 0.02 mol L⁻¹. l_D± is estimated to be about 2.98 nm.

After acquiring these important parameters, we tried to explain the phenomenon in Fig. 10. From Fig. 4, the polymer solution contains uncompensated charges. In salt-free solutions, the chains are stretched because of the repulsion between the negative charges.¹² When a small amount of salt is added, l_D decreases but is still larger than l_D± (2.98 nm). The salt can screen the repulsion between uncompensated charges with decreasing polymer chain size. At c_NaCl of 1 g L⁻¹, l_D is about 2.29 nm; thus, l_D is approximately equal to l_D± where in the chain size has the lowest value. When more salt is added, l_D is smaller than l_D±; therefore, the attraction between opposite charges in polyzwitterionic coils can be screened by the added salt. As a result, the chain size increases and leads to an apparent increase in viscosity. The above result is also consistent with the theoretical model suggested by Dobrynin and Rubinstein. They discussed various regimes for polyampholyte chains with charge asymmetry in salt solutions. In a no-salt regime, the chains are stretched by excess charges. In a low-salt regime, the chains exhibit polyelectrolyte behaviors. In a high-salt regime, the chains show properties similar to those of polyampholyte.^12,26

4 Conclusions

Hydrophobically modified PSBMA formed micelles even at extremely low concentrations because of hydrophobic block associations. Such hydrophobic interactions are enhanced with increasing polymer concentration. Both PSBMA with and without hydrophobic modification exhibit negative zeta-potential which increases with increasing polymer concentration. The viscosity of P(SBMA–GMA) aqueous solution can be divided into two regions, in which the concentration dependence is η_sp ∝ c^1.1 and η_sp ∝ c^3.2 for dilute and semidilute solutions, respectively. Quite different from typical dilute polymer solutions, P(SBMA–GMA) solution exhibits shear thinning even at c_{P(SBMA–GMA)} < c_η. Under the same high concentration, P(SBMA–GMA) solution behaves like a weak gel (G′ > G′′), while viscosity is dominant in PSBMA solution (G′ < G′′). After shearing, the solution viscosity of P(SBMA–GMA) could be immediately recovered as well as that of PSBMA. The rheological behavior of P(SBMA–GMA) solution shows an unusual relationship with temperature and G′ is much more sensitive to temperature than G′′ because of the existence of hydrophobic association and epoxy groups. Moreover, the viscosity of P(SBMA–GMA) solution is sensitive to the added salt concentration, i.e., the viscosity initially decreases and subsequently increases upon the addition of salt. The critical salt concentration is considered to be related to the Debye length l_D of salt solution and to the average microscopic distance between ammonium and sulfonate charges confined inside a polyzwitterionic coil. These excellent properties provide many applications in various regions, such as repellant oil agent, cosmetic, water treatment agent, etc.

Acknowledgements

This research was supported by the National Natural Science Foundation of China (Grant 20674072, 51173164).

References

1. K. Ishihara, H. Nomura, T. Mihara, K. Kurita, Y. Iwasaki and N. Nakabayashi, J. Biomed. Mater. Res., 1998, 39, 323–330.
2. Y. Iwasaki, S. Sawada, K. Ishihara, G. Khang and H. B. Lee, Biomaterials, 2002, 23, 3897–3903.
3. T. Nakaya and Y. J. Li, Prog. Polym. Sci., 1999, 24, 143–181.
4. G. Cheng, G. Z. Li, H. Xue, S. F. Chen, J. D. Bryers and S. Y. Jiang, Biomaterials, 2009, 30, 5234–5240.
5. Z. Zhang, J. A. Finlay, L. F. Wang, Y. Gao, J. A. Callow, M. E. Callow and S. Y. Jiang, Langmuir, 2009, 25, 13516–13521.
6. L. Carr, G. Cheng, H. Xue and S. Y. Jiang, Langmuir, 2010, 26, 14793–14798.
7. J. C. Hower, Y. He, M. T. Bernards and S. Y. Jiang, J. Chem. Phys., 2006, 125, 214704–214711.
8. B. D. Ratner and S. J. Bryant, Annu. Rev. Biomed. Eng., 2004, 6, 41–75.
9. R. Langer, Science, 2001, 293, 58–59.
10. K. L. Prime and G. M. Whitesides, Science, 1991, 252, 1164–1167.
11. A. Ohlemacher, F. Candau, J. P. Munch and S. J. Candau, J. Polym. Sci., Part B: Polym. Phys., 1996, 34, 2747–2757.
12. A. V. Dobrynin and M. Rubinstein, J. Phys. II, 1995, 5, 677–695.
13. P. G. Higgs and J. F. Joanny, J. Chem. Phys., 1991, 94, 1543–1554.
14. A. Diehl, M. C. Barbosa and Y. Levin, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54, 6516–6525.
15. A. V. Dobrynin and M. Rubinstein, Prog. Polym. Sci., 2005, 30, 1049–1118.
16. A. Parker and W. Fieber, Soft Matter, 2013, 9, 1203–1213.
17. M. Skouri, J. P. Munch, S. J. Candau, S. Neyret and F. Candau, Macromolecules, 1994, 27, 69–76.
18. S. V. Singh, P. K. Singh, A. V. Singh, J. S. Sohal, V. K. Gupta and V. S. Vihan, Vaccine, 2007, 25, 7102–7110.
19. A. B. Lowe and C. L. McCormick, Chem. Rev., 2002, 102, 4177–4189.
20. C. L. McCormick and C. B. Johnson, Polymer, 1990, 31, 1100–1107.
21. C. L. McCormick and L. C. Salazar, Polymer, 1992, 33, 4384–4387.
22. P. Mary, D. D. Bendejacq, M. P. Labeau and P. Dupuis, J. Phys. Chem. B, 2007, 111, 7767–7777.
23. G. Z. Zheng, G. Meshitsuka and A. Ishizu, J. Polym. Sci., Part B: Polym. Phys., 1995, 33, 867–877.
24. C. L. McCormick and L. C. Salazar, Macromolecules, 1992, 25, 1896–1900.
25. R. G. Ezell, I. Gorman, B. Lokitz, N. Treat, S. D. McConaughy and C. L. McCormick, J. Polym. Sci., Part A: Polym. Chem., 2006, 44, 4479–4493.
26. A. V. Dobrynin, R. H. Colby and M. Rubinstein, J. Polym. Sci., Part B: Polym. Phys., 2004, 42, 3513–3538.
27. A. A. Abdala, W. J. Wu, K. R. Olesen, R. D. Jenkins and S. A. Khan, J. Rheol., 2004, 48, 979–994.
28. M. A. Winnik and A. Yekta, Curr. Opin. Colloid Interface Sci., 1997, 2, 424–436.
29. R. D. Hester and D. R. Squire, J. Coat. Technol., 1997, 69, 109–114.
30. K. C. Taylor and H. A. Nasr-El-Din, J. Pet. Sci. Eng., 1998, 19, 265–280.
31. E. Volpert, J. Selb and F. Candau, Polymer, 1998, 39, 1025–1033.
32. A. Hill, F. Candau and J. Selb, Macromolecules, 1993, 26, 4521–4532.
33. S. Choudhary and S. R. Bhatia, Carbohydr. Polym., 2012, 87, 524–530.
34. O. Borisova, L. Billon, M. Zaremski, B. Grassl, Z. Bakaeva, A. Lapp, P. Stepanek and O. Borisov, Soft Matter, 2011, 7, 10824–10833.
35. E. K. Penott-Chang, L. Gouveia, I. J. Fernandez, A. J. Muller, A. Diaz-Barrios and A. Eduardo Saez, Colloids Surf., A, 2007, 295, 99–106.
36. H. Chen, Z. M. Wang, Z. B. Ye and L. J. Han, J. Appl. Polym. Sci., 2014, 131(1), 39707.
37. Y. J. Che, Y. B. Tan, J. Cao and G. Y. Xu, J. Macromol. Sci., Part B: Phys., 2010, 49, 695–710.
38. L. E. Bromberg and D. P. Barr, Macromolecules, 1999, 32, 3649–3657.
39. M. Wilhelm, C. L. Zhao, Y. C. Wang, R. L. Xu, M. A. Winnik, J. L. Mura, G. Riess and M. D. Croucher, Macromolecules, 1991, 24, 1033–1040.
40. L. E. Bromberg and D. P. Barr, Biomacromolecules, 2000, 1, 325–334.
41. Z. Iatridi and C. Tsitsilianis, Soft Matter, 2013, 9, 185–193.
42. Y. J. Che, Y. B. Tan, J. Cao and G. Y. Xu, J. Macromol. Sci., Part B: Phys., 2010, 49, 695–710.
43. P. N. Nesterenko and P. R. Haddad, Anal. Sci., 2000, 16, 565–574.
44. A. S. Kimerling, W. E. Rochefort and S. R. Bhatia, Ind. Eng. Chem. Res., 2006, 45, 6885–6889.
45. A. Niu, D. J. Liaw, H. C. Sang and C. Wu, Macromolecules, 2000, 33, 3492–3494.
46. W. F. Lee and C. C. Tsai, Polymer, 1995, 36, 357–364.
47. B. Nystrom, A. L. Kjoniksen, B. Ni, K. Z. Zhu and K. D. Knudsen, Soft Matter, 2009, 5, 1328–1339.
48. J. P. Celli, B. S. Turner, N. H. Afdhal, R. H. Ewoldt, G. H. McKinley, R. Bansil and S. Erramilli, Biomacromolecules, 2007, 8, 1580–1586.
49. C. Chassenieux, T. Nicolai and L. Benyahia, Curr. Opin. Colloid Interface Sci., 2011, 16, 18–26.
50. E. J. Regalado, J. Selb and F. Candau, Macromolecules, 1999, 32, 8580–8588.
51. R. H. Colby, Rheol. Acta, 2010, 49, 425–442.
52. P. Kujawa, A. Audibert-Hayet, J. Selb and F. Candau, Macromolecules, 2006, 39, 384–392.
53. M. Rubinstein and A. N. Semenov, Macromolecules, 2001, 34, 1058–1068.
54. L. Jin, Y. G. Shangguan, T. Ye, H. Yang, Q. F. An and Q. Zheng, Soft Matter, 2013, 9, 1835–1843.
55. Q. Wu, M. Du, T. Ye, Y. G. Shangguan, J. P. Zhou and Q. Zheng, Colloid Polym. Sci., 2009, 287, 911–918.
56. C. L. McCormick, T. Nonaka and C. B. Johnson, Polymer, 1988, 29, 731–739.
57. P. Setny, R. Baron and J. A. McCammon, J. Chem. Theory Comput., 2010, 6, 2866–2871.
58. Y. X. Zhang, A. H. Da, G. B. Butler and T. E. Hogenesch, J. Polym. Sci., Part A: Polym. Chem., 1992, 30, 1383–1391.
59. R. G. Ezell and C. L. McCormick, J. Appl. Polym. Sci., 2007, 104, 2812–2821.
60. Y. Umar, B. F. Abu-Sharkh and S. A. Ali, Polymer, 2005, 46, 10709–10717.
61. D. N. Schulz, D. G. Peiffer, P. K. Agarwal, J. Larabee, J. J. Kaladas, L. Soni, B. Handwerker and R. T. Garner, Polymer, 1986, 27, 1734–1742.
62. D. Leckband and J. Israelachvili, Q. Rev. Biophys., 2001, 34, 105–267.

---