Passivation of native defects of ZnO by doping Mg detected through various spectroscopic techniques

Abstract

Native defects, responsible for the n-type behavior of ZnO are found to be reduced by Mg doping. Zn_1−xMg_xO nanoparticles synthesized by the conventional coprecipitation route are characterized by XRD, TEM and various spectroscopic techniques like FTIR, XPS, UV-visible, PL, Raman and PAS. Unintentional hydrogen and complex defects in addition to cationic and anionic vacancies (V_Zn and V_O) in ZnO nanoparticles are observed from FTIR. After incorporating Mg, an additional IR mode at 856 cm⁻¹ is observed and attributed to Mg–H. The additional mode contributing excess hydrogen in Mg doped ZnO is further confirmed from XPS. PL and PAS measurements indicate less native defects in Mg doped ZnO because of passivation of defects by excess hydrogen. We conclude that Mg doping not only diminishes the native defects in ZnO, but also could be used as a suitable material for hydrogen storage.

---

Introduction

ZnO, a wide band gap semiconductor, has been extensively studied due to its multifunctional properties and potential applications in devices like ultraviolet light emitting diodes, field effect transistors, lasers, gas sensors and resonators.^1–4 A major drawback in ZnO is the fact that it always shows n-type conductivity. One of the widely accepted reasons is the presence of native defects such as zinc interstitial sites (Zn_i) or oxygen vacancies (V_O).^5,6 However, Van de Walle predicts a new source of the observed conductivity, which is hydrogen atoms.⁷ In most of the semiconductors, hydrogen acts as a compensating centre counteracting the existing conductivity. However, in ZnO, the behaviour of hydrogen is amphoteric. The hydrogen atom acts as a shallow donor when present in the interstitial site of ZnO lattice. It may present in ZnO or transition metal (TM) doped ZnO in the form of H_i (interstitial) or complexes like V_Zn–H and TM_Zn–H.⁸ Wardle et al. suggests that hydrogen complexes in ZnO are stable shallow donor systems at room temperature rather than isolated H_i.⁸ Hydrogen related defect complexes such as V_Zn–H and TM_Zn–H have been observed in other metal oxides like MgO, CaO, SrO and Mg doped GaN.^9–13 The source of hydrogen in ZnO is the water which is used as solvent during chemical synthesis. The ZnO surface is able to split the water and generate hydrogen.¹⁴ It is reported that the water-splitting phenomenon is enhanced after doping Al or Mg in ZnO.^15,16 Therefore, the hydrogen generated on the surface of ZnO due to the water splitting is responsible for the formation of complexes like V_Zn–H and TM_Zn–H. On the other hand, the source of hydrogen could be hydroxyl ions (OH⁻) which sometimes serve as passivator for acceptors.¹⁷ In particular, passivation of acceptors (native defects or impurities) by hydrogen or hydroxyl ions (OH⁻) has been identified as a serious problem for p-type doping.¹⁸ The identification and removal of these native defects and undesired impurities introduced during or after material growth that hinders the development of efficient ZnO based optoelectronic devices is still a great challenge for the researchers.

The present work is undertaken to capture the defects after doping Mg in ZnO prepared by conventional coprecipitation route. It is shown that upto 15% of Mg, wurtzite phase of ZnO remains unchanged. While FTIR shows clear evidence of magnesium related peak (V_Mg–H/OH) in Mg doped ZnO, XPS shows more hydrogen impurity in Mg doped ZnO than pure ZnO. Both, photoluminescence and positron annihilation spectroscopic techniques provide additional support for reduction of native defects and at the same time capacity of hydrogen uptake is enhanced.

Synthesis and characterizations

ZnO and Mg doped ZnO nanoparticles were synthesized by conventional co-precipitation technique. For ZnO desired quantity of zinc nitrate of 1 M solution was taken in a beaker. 2 M aqueous solution of NaOH (A.R. grade) was added drop wise with constant stirring to the zinc nitrate solution till the pH of precipitation attained 11. A white product was obtained after filtering and washing the precipitate several times with distilled water followed by acetone. Zn_1−xMg_xO (x = 0, 0.04, 0.08, 0.12, 0.10, 0.15 and 0.02) samples were made by the same procedure after adding the calculated amount of 1 M solution of Mg(NO₃)₂ to 1 M solution of Zn(NO₃)₂ followed by stirring, precipitating with aqueous solution of NaOH, filtering and washing. Final product of ZnO and Mg doped ZnO were dried at 250 °C for 12 h. The dried powders were characterized by X-ray diffraction (XRD) using an 18 kW rotating anode (Cu Kα) based Rigaku powder diffractometer operating in the Bragg–Brentano geometry and fitted with a graphite monochromator in the diffracted beam. FT-IR data were recorded by SHIMADZU-8400S in the range 500–4000 cm⁻¹. The X-ray photoelectron spectra (XPS) were recorded for identification of oxidation state of zinc, magnesium and oxygen on a X-ray electron spectrometer using Mg K_α radiation. Transmission Electron Microscopy (Model: Tecnai 20 G² FEI) with an acceleration energy of 100 keV was used for the phase and microstructural studies. The elemental detection was carried out by EDS (From OXFORD instruments). Photoluminescence (PL) spectra were recorded using pulsed Nd:YAG laser (Spitlight600, Innolas, Germany) as a light source (λ = 266 nm) and a spectrometer (Ocean Optics QE65000) for recording the emission spectra. Optical band gap was estimated by using double beam UV-visible spectrophotometer (SHIMADZU-2450). Raman scattering was performed on a micro-Raman setup (Renishaw, UK) equipped with a grating of 1800 lines per mm and a peltier cooled charge coupled device (CCD) detector. The Ar⁺ laser (514.5 nm) was used as an excitation source. A microscope from Olympus (Model: MX50 A/T) was attached with the spectrometer, which focuses the laser light on to the sample and the GRAM-32 software was employed for data collection. Positron annihilation lifetime (PAL) measurement was carried out using a fast–fast coincidence system consisting of two 1 in. tapered off BaF₂ scintillators coupled to XP 2020Q photomultiplier tube. The prompt time resolution of the system using a ⁶⁰Co source with ²²Na gate was 298 ps. The lifetime spectra were deconvoluted using the code PATFIT 88.

Results and discussion

In X-ray diffraction pattern of pure and Zn_1−xMg_xO (0.04 ≤ x ≤ 0.20) are depicted in Fig. 1a. Up to x = 0.15 of Mg doping, all observed peaks are indexed with the wurtzite phase (JCPDS 89-1397) of ZnO. No additional peaks within the detection limit of XRD is observed indicating neither any structural changes nor formation of additional phases in ZnO up to x = 0.15. Mg(OH)₂ (JCPDS 07-0239) as an impurity phase is observed at x = 0.20 and marked as “*” in Fig. 1a. Reported results shows the solubility limit of Mg in ZnO is ≤0.15,^19,20 comparable to the present case. XRD peak corresponding to (101) plane with increasing Mg concentration shifts towards higher 2θ value indicating the decrease in lattice parameter, shown in Fig. 1b. We have analysed the lattice parameter and found decrease in c/a ratio with increase in x (0 ≤ x ≤ 0.15) by using Fullprof software for Le Bail refinement at constant scale factor (Table 1). Further, the strain and crystallite size are calculated from the Williamson–Hall plot shown in Fig. 2 with the help of eqn (1).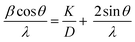where β is full width at half maximum (FWHM) of various Bragg peaks measured after removing the Kα₂ contribution and the instrumental broadening effects, θ is the Bragg angle. Eqn (1) represents a straight line. K/D is the intercept of the straight line, where K is constant and D stands for the crystallite size. Slope of eqn (1) gives the strain in the lattice. Strain and crystallite size with varying the x (0 ≤ x ≤ 0.15) are tabulated in Table 1.

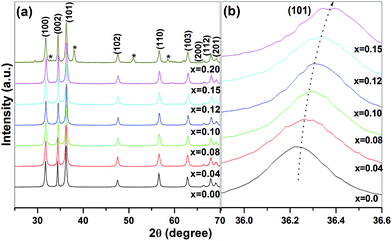Fig. 1 (a) X-ray diffraction pattern of Zn_1−xMg_xO (x = 0, 0.04, 0.08, 0.10, 0.12, 0.15 and 0.20) nanoparticles. (b) The magnified view of the peak corresponding to (101) plane.

Table 1 c/a ratio from Le Bail refinement, crystallite size and strain calculation from the Williamson–Hall plots are shown

Sample name (P63mc)	c/a	Strain	Crystallite size (D)
089-1397	1.6025	—	—
ZnO	1.6022	0.21537	11 ± 3
Zn0.96Mg0.04O	1.6017	0.20583	8 ± 2
Zn0.92Mg0.08O	1.6010	0.19335	8 ± 2
Zn0.90Mg0.10O	1.6009	0.18215	8 ± 1
Zn0.88Mg0.12O	1.6005	0.17653	6 ± 1
Zn0.85Mg0.15O	1.6018	0.1904	7 ± 2

---

Fig. 2 Williamson–Hall plots for Zn_1−xMg_xO (x = 0, 0.04, 0.08, 0.10, 0.12 and 0.15) nanoparticles.

With increase in x (0 ≤ x ≤ 0.15), strain as well as c/a ratio obtained from Le Bail profile fitting shows a decreasing trend upto 12% of Mg. It has been reported in the materials like SnO₂, TiO₂, ZnO etc., strain in the lattice is due to the defects or lattice disorder.²¹ Reduction of strain in the present case is thus confirmed the reduction of defects in lattice. Further, c/a ratio measures the defects in the lattice. While the theoretical value of c/a ratio for ZnO is 1.602, for doped and undoped ZnO it is reported as 1.599–1.603. The deviation of c/a ratio from the theoretical value shows the presence of defects in ZnO.²² For instance, Mohanty et al. have observed an increase in c/a ratio in ZnO due to large number of zinc interstitials.²² Thus, the decrease in c/a ratio and strain observed in our case indicates the reduction of defects with increase in Mg content. The crystallite size in ZnO found to be of 11 nm which is reduced to ∼7 nm in Mg doped ZnO and does not show significant change with dopant concentration. Several studies report gradual decrease in crystallite size with incorporation of dopants like Mg, Fe and Al in ZnO.²³ Various reasons like compression stress arising due to the difference in the ionic radii of Zn and dopant ion or obstruction of the crystal growth or generation of defects in the crystals due to incorporation of dopant ion could suppress the growth of ZnO.²³ In addition, size of the particle is decided by nucleation and growth process. Decrease in crystallite size thus indicates more nucleation sites and obstruction of growth of ZnO like in Fe doped ZnO.²³

Fig. 3a and b depicts typical TEM micrographs with EDS patterns of ZnO and Zn_0.96Mg_0.04O samples. EDS spectra confirm the presence of Mg in Zn_0.96Mg_0.04O. Selected area electrondiffraction (SAED) pattern of both the samples reveals self-organization of nanoparticles and single crystalline nature. While the homogeneous particle size distribution with size about 18 nm in ZnO is observed, in Zn_0.96Mg_0.04O sample with a broad particle size distribution of nanorods having aspect ratio 1 : 4 is detected.

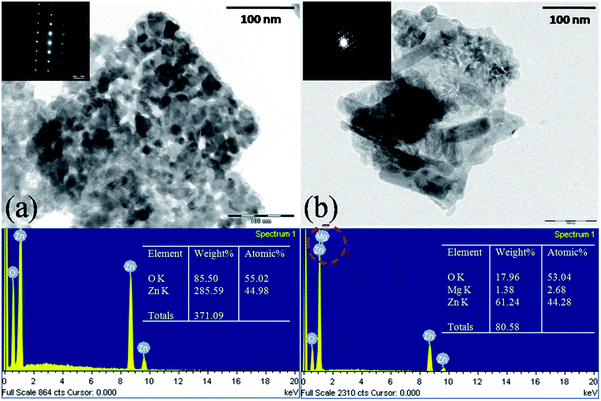Fig. 3 Transmission Electron Micrographs of (a) ZnO and (b) Zn_0.96Mg_0.04O nanoparticles with EDS spectra. Inset shows the SAED pattern of respective samples.

Typical photoluminescence spectra of ZnO and Zn_0.96Mg_0.04O are shown in Fig. 4. One intense UV emission peak at about ∼3.19 eV (389 nm) and a broad hump in the range of 2.4 to 1.77 eV (516 nm to 700 nm) for an excitation wave length 266 nm have been seen. UV emission at 3.19 eV is due to the recombination through free excitons and is known as near band edge (NBE) emission. It has been reported by Ke et al. that optical transition occurs in green (2.32 eV), green-yellow (2.21 eV) and yellow-orange (2.07 eV) zones for ZnO. While green emission is ascribed to Zn vacancies, green-yellow emission is likely due to O vacancies and yellow-orange emission may be caused by O interstitials.²⁴ Therefore, the latter broad emission could be mediated by some deep level defects or vacancies due to impurities in the present case. However, Mg inclusion suppresses the broad emission. Improvement in UV emission efficiency of Mg doped ZnO is ascribed to the diminution of active centres, which are responsible for the origin of visible emission.²⁵ UV emission in both the samples as well as the improvement of UV emission in Mg doped ZnO is well matched with the optical band gap obtained from UV-visible spectroscopy. A clear shift in absorption onset towards blue is observed in Mg doped ZnO (inset of Fig. 4.), indicating an increase in band gap. Thus PL studies clearly show the reduction or passivation of native defects in Zn_0.96Mg_0.04O nanoparticles compared to ZnO.

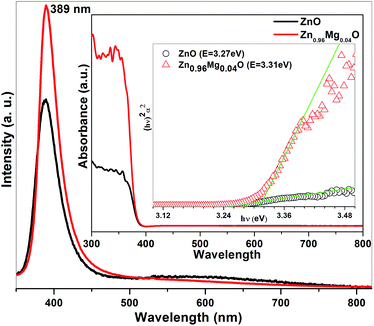Fig. 4 Photoluminescence spectra of ZnO and Zn_0.96Mg_0.04O nanoparticles. Inset shows the absorbance and (αhν)² vs. hv plot for both samples obtained from UV-visible spectrophotometer.

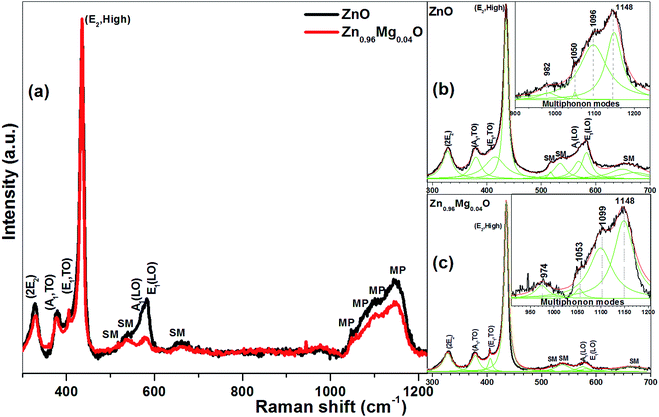
Fig. 5 shows the Raman spectra of ZnO and Zn_0.96Mg_0.04O nanoparticles ranging from 300 to 1400 cm⁻¹ measured at room temperature. Due to overlapped modes, we could not distinguish the individual peaks. The whole spectra are thus deconvoluted into separate peaks by Lorentzian curve fitting shown as Fig. 5b and c. It is clearly seen that reported values of first order Raman modes such as A₁(TO), E₁(TO), E₂(high), A₁(LO), E₁(LO) and second order mode such as 2E₂ are matched well with the experimentally observed Raman modes.^26–28 Besides the first order and second order phonon modes, a few additional modes at about 517, 536, and 649 cm⁻¹ are also observed.^26–28 Similar additional modes have been found in ZnO doped with Ni and Mn at ∼524 and 670 cm⁻¹ and other dopants like Sb, Ga and Fe at 511, 531, 644 and 720 cm⁻¹, respectively.^29,30 The authors have been attributed the origin of these additional modes to intrinsic host-lattice defects related to doping. Manjon et al. have reported that most of the additional Raman modes observed in doped ZnO samples correspond to the silent modes (SM) of ZnO.²⁶ The ab initio calculations have shown the silent modes B₁(low), 2B₂(low), B₁(high), TA + B₁(high) and B₁(low) + B₁(high) obtained at 261, 520, 552, 650 and 810 cm⁻¹ respectively. Additional modes in both pure and doped ZnO in our case are matched with.

Fig. 5 (a) Raman spectra of ZnO and Zn_0.96Mg_0.04O nanoparticles in the range of 300 to 1400 cm⁻¹. The lorentzian fitting of 270–760 cm⁻¹ and 900–1240 cm⁻¹ for (b) ZnO and (c) Zn_0.96Mg_0.04O samples. Here the silent modes and multiphonon modes of ZnO are denoted as SM and MP, respectively.

However, the intensity of these modes decreases in Zn_0.96Mg_0.04O. After deconvolution, the broad band in the range 900 to 1250 cm⁻¹, is fitted with four peaks in ZnO at positions 982, 1050, 1096 and 1148 cm⁻¹ as well as in Zn_0.96Mg_0.04O centred at 974, 1053, 1099 and 1148 cm⁻¹ represent the multiphonon modes (MP) and are matched well with reported values.²⁶ The peaks at 583 and 1148 cm⁻¹ are assigned as first order and second order of E₁(LO) mode respectively as a consequence of defects such as O-vacancies, Zn interstitials, or these complexes.³¹ The ratio of E₁(LO) and E_2,High (characteristic of wurtzite structure); which tells quantitatively about the presence of defects are found to be higher in ZnO than in Zn_0.96Mg_0.04O, well corroborates with the PL results.

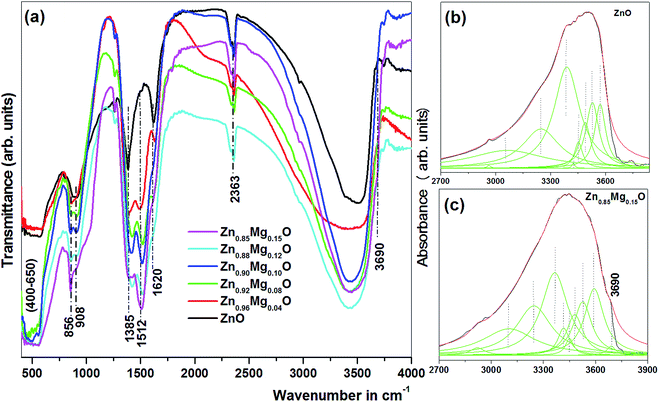
Atomic vibrational modes of pure and Mg doped ZnO are examined by Fourier Transform of the Infrared spectrometer (FTIR) as shown in Fig. 6a. Peak at around 2363 cm⁻¹ is caused by a small amount of residual CO₂. Two peaks observed at 1261 and 1385 cm⁻¹ correspond to residual NO₃⁻ ion which could not be removed completely after washing. A broad band between 400 and 650 cm⁻¹ represents the stretching mode of Zn–O.³² The band centred at 1620 cm⁻¹ is the bending vibrational mode of hydroxyl group of the chemisorbed and/or physiosorbed water molecules.³³ A broad band around 3000–3700 cm⁻¹ corresponds to the O–H bond stretching local vibrational modes (LVM). After deconvolution of broad band, peaks at 3251, 3384, 3452, 3492, 3532 and 3575 cm⁻¹ have been obtained in ZnO and Mg doped ZnO (Fig. 6b and c). The peaks are assigned to interstitial hydrogen bonded with oxygen in bond-center and anti-bonding position as well as with vacant zinc site (V_Zn) in parallel and perpendicular alignment to the c-axis.³⁴ The observed modes are compared with both theoretically and experimentally reported values and are found to be in between the limit of theoretically and experimentally reported values.^8,35 A prominent band at 908 cm⁻¹ observed in ZnO corresponds to the bending vibration of V_Zn-H_ABO∥.⁸ Besides the above common modes, a few additional modes are also observed at 856, 1512 and 3690 cm⁻¹ in Mg doped ZnO. Comparing the modes of ZnO and Mg doped ZnO at 908 and 856 cm⁻¹, one may note that, while the higher wave number is assigned to Zn–H as per the literatures, the lower one could be due to Mg–H as per the relationship (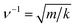) where the wave number is proportional to mass of ions. As Mg is having lower mass than Zn, so Zn–H band occurs at higher wave number than Mg–H. The increase in intensity of the Mg–H band with Mg content further confirms that the band must be associated with Mg. Other two bands also become more pronounced with higher concentration of Mg shown in Fig. 6a. All three modes scale in intensity with magnesium content which further indicates that the above modes are due to vibrations of different Mg–H complexes. Local vibrational modes of the Mg_Ga–H complexes have also been identified through infrared absorption measurements in Mg doped GaN at 3125 cm⁻¹.¹³ Gonzalez et al. have reported Mg–H band at 1000 cm⁻¹ and a band at 3700 cm⁻¹ for Mg(OH)₂ precipitates in MgO.⁹ One may clearly see in our case that the peaks at 908 cm⁻¹ and 1512 cm⁻¹ in ZnO are splitted into two peaks after Mg doping. Therefore, the additional mode at 856 cm⁻¹ could be attributed to Mg–H and modes at 1512 and 3690 cm⁻¹ to Mg–OH band. The amount of hydrogen impurity is thus found to be higher in Mg doped ZnO. This is possible due to high hydrogen storage capacity of Mg.³⁶ Similar occurrence of higher hydrogen content in Zn_0.96Mg_0.04O nanowire than that of ZnO nanowire have been found by Pan et al. through hydrogen absorption measurements.¹⁶ Gonzalez et al. have reported that if hydrogen impurities are present in the crystal, it is expected that they can be trapped at oxygen-vacancy sites and form H⁻ ions.⁹ Gotz et al. have also established in Mg doped GaN that Mg acceptors are passivated by hydrogen.¹¹ Thus, one expects the excess hydrogen in Mg doped ZnO may passivate more vacancies compared to pure ZnO and results in less native defects contributing to defect emission in PL spectrum as observed in our case.

Fig. 6 (a) FT-IR transmittance spectra of Zn_1−xMg_xO (x = 0, 0.04, 0.08, 0.12, 0.10 and 0.15) nanoparticles (left side) and the Lorentzian fitting of absorbance plot for the (b) ZnO and (c) Zn_0.85Mg_0.15O nanoparticles in range of 2500–3900 cm⁻¹.

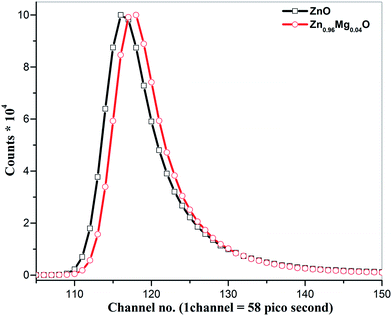
Positron annihilation measurement is further used as a complementary technique to further probe the defects, shown in Fig. 7. The positron annihilation life time τ₁ is 150 ps for Zn_0.96Mg_0.04O which is lower than that of τ₁ (186 ps) of ZnO nanoparticles and is comparable to that of bulk ZnO (158 ps). It has been calculated theoretically that if hydrogen is attached to V_Zn, the positron life time decreases successively.^37,38 For example, while a hydrogen attached to V_Zn yields a positron life time of ∼200 ps while four hydrogens attached to zinc vacancy reduces the life time to 158–162 ps.^37,38 Therefore, τ₁ in ZnO and Zn_0.96Mg_0.04O matches well with the life time of V_Zn attached to one and four hydrogens respectively which further support the FTIR results. The behaviour of τ₂ is characteristic of positron annihilation at the larger defects sites like cluster of vacancy, trapped positrons in nanovoids at the intersection of three or more grain boundaries (e.g., triple junction).³⁹ In the present case, these vacancy sites are made up of multiples of the Zn + O divacancies.⁴⁰ Depending upon the size, vacancies could be a cluster of 2 to 6 di-vacancies (V_Zn+O) and subsequently the life time of positron annihilation increases from 265 ps to 375 ps.⁴⁰ The life time 368 ps obtained for τ₂ in ZnO is in between the life time of positron annihilation corresponding to cluster of 5 and 6 (Zn + O) di-vacancies. However, in Zn_0.96Mg_0.04O, the decrease in τ₂ (306 ps) further indicates the passivation of divacancies by hydrogen or the reduction in the size of Zn + O divacancies. From this study, we conclude that the native defects in ZnO are significantly reduced or passivated by Mg doping.³⁷ Hydrogen is responsible for the passivation of such defects and the formation of V_Zn–H and Mg–H type of defect complexes.

Fig. 7 Positron lifetime spectra of ZnO and Zn_0.96Mg_0.04O nanoparticles.

To understand the chemical bonding in ZnO and Zn_1−xMg_xO nanopowders, the core levels of Zn 2p, Mg 1s and O 1s states are examined using XPS techniques as shown in Fig. 8a and c, respectively. The charge shifted spectra are corrected using the adventitious C 1s photoelectron signal at 284.6 eV. In ZnO sample, the asymmetric O 1s peak is observed with shoulder at higher binding energy side. With the help of XPS Peak Version 4.1, the O 1s peak is deconvoluted into three peaks such as peak 1, 2 and 3 at 530.12, 531.3 and 532.5 eV, respectively. The peak 1 corresponds to the O–Zn bonding, peak 2 is associated with O²⁻ ions in oxygen deficient regions within the matrix of ZnO or the O–H surface adsorbed group on the ZnO surface, whereas the peak 3 is correlated to H/H₂O species.^41–43 The deconvolution in other spectra of O 1s peak for Zn_1−xMg_xO (4 ≤ x ≤ 0.15) samples has been done by fixing the peak positions at 530.12, 531.3 and 532.5 eV in order to compare the intensity of individual peak. The asymmetric O 1s peak maxima from lower binding energy side gradually shifts towards the higher binding energy as x (0 ≤ x ≤ 0.15) increases. The intensity of peak 1 is found to be most intense compared to 2 & 3 peaks in ZnO. However, with increasing x (0 ≤ x ≤ 0.15), the intensity of peak 3 is gradually increased at the expense of peak 1. The increase in intensity of peak 3 with x, thus confirms the excess H/H₂O species. The binding energies corresponding to 1021.3 eV and 1044.5 eV are attributed to the 2p_3/2 and 2p_1/2 core levels of Zn ions, confirming the divalent Zn ions. With increasing x (0 ≤ x ≤ 0.15), Zn 2p_3/2 and 2p_1/2 peaks shift towards higher binding energy with decrease in relative intensity. The shift indicates the Mg and/or Mg–H incorporation into Zn site.^42,44 The Mg 1s peak centred at 1304.5 eV is ascribed to the presence of Mg²⁺ replacing Zn²⁺.

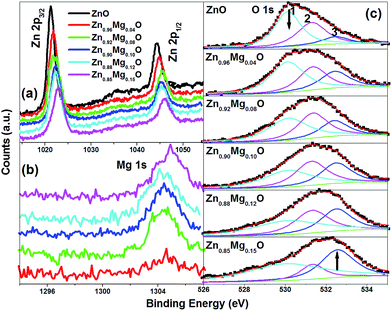Fig. 8 XPS spectra of Zn_1−xMg_xO (x = 0, 0.04, 0.08, 0.12, 0.10 and 0.15) nanoparticles (a) for Zn 2p_3/2 and 2p_1/2, (b) for Mg 1s and (c) For O 1s.

ZnO, a well studied n-type semiconductor, shows many vibrational frequencies like H_i at antibonding site (AB_O, ⊥), H_i at bond centred position (BC_∥), V_Zn–H, V_Zn–H₂, Zn–H_O and O–H etc. whose origins are still puzzling. However, the interaction of ubiquitous impurity like H with ZnO has many important technological implications. For example, H is expected to become an environmentally benign fuel in future and nanoparticles of ZnO can be a potential material for hydrogen sensor. Moreover, ZnO may be considered as a prospective material for hydrogen storage in future. We have shown clearly the additional vibrational modes at 908 cm⁻¹ and 1512 cm⁻¹ after Mg doping which is attributed to Mg–H and Mg–OH bond, respectively. The increase in intensity of above bands with increase in Mg concentration further shows the evidence of excess H/H₂O species in XPS spectra. Although the source of hydrogen is due to the adsorption of H₂O on ZnO surface during conversion of zinc hydroxide to zinc oxide, H₂O is dissociated into H⁺ and OH⁻ and remain attached to the surface which we detect.⁴⁵ The above process speeds up with doping Mg in the ZnO lattice, because MgO surface is more sensitive for dissociation of H₂O.⁴⁶ The dissociation of water occurs at the site of the defects rather than physisorption. The defects change the physical and chemical properties and even increases the dissociation energies.⁴⁴ The defects such as zinc vacancy (V_Zn) and cluster of Zn + O di-vacancies (V_Zn+O) might be responsible for dissociation of water in the present case. Therefore, Mg doped ZnO samples synthesized by easy and cost effective conventional coprecipitation technique could be a useful futuristic material not only for hydrogen sensor, but also can be used as photocatalysts, hydrogen storage material etc.

Conclusions

ZnO and Mg doped ZnO nanoparticles synthesized through conventional coprecipitation route showed defects related to local vibrational modes of hydrogen as it has been reported in single crystals and thin films of ZnO. Although, XRD showed pure wurtzite phase, Raman spectra revealed few additional modes corresponding to silent modes such as 2B₂(low), B₁(high) and TA + B₁(high) of ZnO, which were suppressed after Mg doping. FTIR spectra demonstrated the presence of cationic vacancies in addition to unintentional hydrogen doping and their complexes in ZnO and Mg–H defect complex in Zn_1−xMg_xO (0.04 ≤ x ≤ 0.20). Positron life time measurement, Raman and photoluminescence studies confirmed that after Mg incorporation in ZnO lattice, the native defects were reduced or passivated by the hydrogen significantly. XPS confirmed the excess hydrogen in Mg doped ZnO sample.

Acknowledgements

UGC-DAE Consortium for Scientific Research, Kolkata Centre, is acknowledged for providing the PAS facility. The authors thank Prof. O.N. Srivastava for providing TEM facility and Dr A.K. Mishra for the help in PAS data analysis. V.P. Singh acknowledges CSIR, India, for providing senior research fellowship.

References

1. J. H. He, S. T. Ho, T. B. Wu, L. J. Chen and Z. L. Wang, Chem. Phys. Lett., 2007, 435, 119.
2. M. H. Huang, S. Mao, H. Feick, H. Yan, Y. Wu, H. Kind, E. Weber, R. Russo and P. D. Yang, Science, 2001, 292, 1897.
3. M. S. Arnold, P. Avouris, Z. W. Pan and Z. L. Wang, J. Phys. Chem. B, 2003, 107, 659.
4. H. Kind, H. Q. Yan, B. Messer, M. Law and P. D. Yang, Adv. Mater. (Weinheim, Ger.), 2002, 14, 158.
5. D. C. Look, J. W. Hemsky and J. R. Sizelove, Phys. Rev. Lett., 1999, 82, 2552 and references therein.
6. P. Kasai, Phys. Rev. B: Solid State, 1963, 130, 989.
7. C. G. Van de Walle, Phys. Rev. Lett., 2000, 85, 1012.
8. M. G. Wardle, J. P. Goss and P. R. Briddon, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 155108.
9. R. Gonzalez, Y. Chen and M. Mostoller, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 24(no. 12), 6862.
10. M. G. Weinstein, C. Y. Song, M. Stavola, S. J. Pearton and R. G. Wilson, Appl. Phys. Lett., 1998, 72(no. 14), 6.
11. W. Gotz, N. M. Johnson, D. P. Bour, M. D. McCluskey and E. E. Haller, Appl. Phys. Lett., 1996, 69(24), 9.
12. A. Kaschner, H. Siegle, G. Kaczmarczyk, M. Straßburg and A. Hoffmann, Appl. Phys. Lett., 1998, 72, 1703.
13. R. Cusco, L. Artus and D. Pastor, Appl. Phys. Lett., 2004, 84, 6.
14. X. Ma and M. R. Zachariah, Int. J. Hydrogen Energy, 2010, 35, 2268.
15. C. H. Hsu and D. H. Chen, Int. J. Hydrogen Energy, 2011, 36, 15538.
16. H. Pan, J. Luo, H. Sun, Y. Feng, C. Poh and J. Lin, Nanotechnology, 2006, 17, 2963.
17. J. Čížek, N. Žaludová, M. Vlach, S. Daniš, J. Kuriplach, I. Procházka, G. Brauer, W. Anwand, D. Grambole, W. Skorupa, R. Gemma, R. Kirchheim and A. Pundt, J. Appl. Phys., 2008, 103, 053508.
18. A. Tsukazaki, A. Ohtomo, T. Onuma, M. Ohtani, T. Makino, M. Sumiya, K. Ohani, S. F. Chichibu, S. Fuke, Y. Segawa, H. Ohno, H. Koinuma and M. Kawasaki, Nat. Mater., 2005, 4, 42.
19. P. Kumar, J. P. Singh, Y. Kumar, A. Gaur, H. K. Malik and K. Asokan, Curr. Appl. Phys., 2012, 12, 1166.
20. A. Ohtomo, R. Shiroki, I. Ohkubo, H. Koinuma and M. Kawasaki, Appl. Phys. Lett., 1999, 75(no. 26), 4088.
21. F. Gu, S. F. Wang, M. K. Lü, G. J. Zhou, D. Xu and D. R. Yuan, J. Phys. Chem. B, 2004, 108, 8119; P. Ghosh and A. Patra, J. Phys. Chem. C, 2007, 111, 7004; K. C. Barick, M. Aslam, V. P. Dravid and D. Bahadur, J. Colloid Interface Sci., 2010, 349, 19; R. Sendi and S. Mahmud, J. Phys. Sci., 2013, 24, 1.
22. G. P. Mohanty and L. V. Azároff, J. Chem. Phys., 1961, 35, 1268; R. E. Marotti, D. N. Guerra, C. Bello, G. Machado and E. A. Dalchiele, Sol. Energy Mater. Sol. Cells, 2004, 82, 85; G. Machado, D. N. Guerra, D. Leinen, J. R. Ramos-Barrado, R. E. Marotti and E. A. Dalchiele, Thin Solid Films, 2005, 490, 124.
23. R. S. Kumar, R. Sathyamoorthy, P. Sudhagar, P. Matheswaran, C. P. Hrudhya and Y. S. Kang, Phys. E, 2011, 43, 1166; S. Hartner, M. Ali, C. Schulz, M. Winterer and H. Wiggers, Nanotechnology, 2009, 20, 445701; S. F. Shayesteh and A. A. Dizgah, Pramana, 2013, 81(no. 2), 319; Z. C. Chen, L. J. Zhuge, X. M. Wu and Y. D. Meng, Thin Solid Films, 2007, 515, 5462.
24. L. Ke, S. C. Lai, J. D. Ye, V. L. Kaixin and S. J. Chua, J. Appl. Phys., 2010, 108, 084502.
25. N. Ohashi, T. Ishigaki, N. Okada, H. Taguchi, I. Sakaguchi, S. Hishita, T. Sekiguchi and H. Haneda, J. Appl. Phys., 2003, 93, 6386.
26. F. J. Manjón, B. Marí, J. Serrano and A. H. Romero, J. Appl. Phys., 2005, 97, 053516.
27. F. Decremps, J. Pellicer-Porres, A. M. Saitta, J. C. Chervin and A. Polian, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 092101.
28. R. Cuscó, E. Alarcón-Lladó, J. Ibáñez, L. Artús, J. Jiménez, B. Wang and M. J. Callahan, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 165202.
29. H. Wang, Y. Chen, H. B. Wang, C. Zhang, F. J. Yang, J. X. Duan, C. P. Yang, Y. M. Xu, M. J. Zhou and Q. Li, Appl. Phys. Lett., 2007, 90, 052505.
30. C. Bundesmann, N. Ashkenov, M. Schubert, D. Spemann, T. Butz, E. M. Kaidashev, M. Lorenz and M. Grundmann, Appl. Phys. Lett., 2003, 83(no. 10), 1976.
31. A. K. Pradhan, K. Zhang, G. B. Loutts, U. N. Roy, Y. Cui and A. Burger, J. Phys.: Condens. Matter, 2004, 16, 7123.
32. R. N. Gayen, S. N. Das, S. Dalui, R. Bhar and A. K. Pal, J. Cryst. Growth, 2008, 310, 4073.
33. H. Noei, H. Qiu, Y. Wang, E. Loffler, C. Wollb and M. Muhler, Phys. Chem. Chem. Phys., 2008, 10, 7092.
34. M. G. Wardle, J. P. Goss and P. R. Briddon, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 155108; Y. R. Park and Y. S. Kim, J. Mater. Res., 2008, 23, 1674; V. P. Singh, D. Das and C. Rath, Mater. Res. Bull., 2013, 48, 682.
35. Y. R. Park and Y. S. Kim, J. Mater. Res., 2008, 23, 1674.
36. R. Yu and P. K. Lam, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37(no. 15), 8730-II and references therein.
37. G. Brauer, W. Anwand, D. Grambole, J. Grenzer, W. Skorupa, J. Čížek, J. Kuriplach, I. Procházka, C. C. Ling, C. K. So, D. Schulz and D. Klimm, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 115212.
38. W. Anwand, G. Brauer, T. E. Cowan, D. Grambole, W. Skorupa, J. Cızek, J. Kuriplach, I. Prochazka, W. Egger and P. Sperr, Phys. Status Solidi A, 2010, 207, 2415.
39. R. Krause-Rehberg and H. S. Leipner, Positron Annihilation in Semiconductors, Springer, Berlin, 1999, ch. 3, p. 61.
40. Z. Q. Chen, M. Maekawa, S. Yamamoto, A. Kawasuso, X. L. Yuan and T. Sekiguchi, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 035210.
41. Y. F. Lu, H. Q. Ni, Z. H. Mai and Z. M. Ren, J. Appl. Phys., 2000, 88, 498.
42. C. C. Lin, H. P. Chen, H. C. Liao and S. Y. Chen, Appl. Phys. Lett., 2005, 86, 183103.
43. M. Valtiner, S. Borodin and G. Grundmeier, Phys. Chem. Chem. Phys., 2007, 9, 2406.
44. B. Panigrahy, M. Aslam and D. Bahadur, J. Phys. Chem. C, 2010, 114, 11758.
45. A. L. Almeida, J. B. L. Martins and C. A. Taft, J. Chem. Phys., 1998, 109, 3671; K. Wegner, H. C. Ly, R. J. Weiss, S. E. Pratsinis and A. Steinfeld, Int. J. Hydrogen Energy, 2006, 31, 55; A. Steinfeld, Int. J. Hydrogen Energy, 2002, 27, 611.
46. W. Langel and M. Parrinello, J. Chem. Phys., 1995, 103, 3240.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra04767f

---