Binding to gold nanoclusters alters the hydrogen bonding interactions and electronic properties of canonical and size-expanded DNA base pairs

Abstract

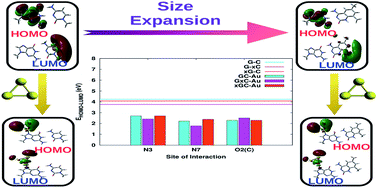
DNA molecules tagged to metal nanoparticles, especially gold nanoparticles (AuNPs), have been shown to have potential applications in the design and fabrication of novel electronic nano-devices, but the binding mechanism between gold nanoparticles and DNA bases and its implications are not completely understood. In this work, a comprehensive study to examine the effect of structural perturbations caused to DNA base pairs in terms of size expansion and adsorption on a gold cluster (Au₃) has been carried out using density functional theory. The geometric and electronic features of these complexes provide evidence for the distortion of certain base pairs depending on the binding site of the cluster. This is further substantiated via normal mode, natural bond orbital (NBO) and atoms in molecules (AIM) analyses. The natural population analysis (NPA) and NBO analysis indicate that complexation greatly affects the charge distribution on the base pairs due to charge transfer between the base pair and gold cluster. This charge redistribution may offer the possibility of higher order interactions. Upon complexation, a marked decrease in the HOMO–LUMO gap is observed, which is more profound in cases where size-expanded bases are involved due to the extended π-conjugation of the fused benzene rings. This study demonstrates the possibility of combining structural modifications to DNA base pairs and subsequent binding to gold nanoparticles to modulate and achieve molecular systems with desired optoelectronic properties.

---

1 Introduction

Conjugated gold nanoparticles blend the distinct properties and functionalities of both clusters and biomolecules, such as strong plasmon absorption bands, the light scattering effect of nanoparticles, and the ability of biological molecules to achieve high specific binding by molecular recognition, justifying their role in developing potential miniature devices.^1–7 In this context, the interaction between biomolecules and nanoparticles is of great significance in laying a foundation for the design of nano-biomolecular devices. The characteristic dependence of the optical, catalytic and electronic properties of the gold nanoparticles (AuNPs) on the conjugating molecules (e.g. biomolecules) makes these complexes even more appealing in designing novel nano-electronic devices.^8–10 Metal nanoparticle complexes with biomolecules find extensive applications in devising novel biosensors, drug/gene delivery agents and imaging devices.^11–19 AuNPs have been found to be very effective in the design of photo-induced control machinery for functional RNA molecules. For example, Matsushita-Ishiodori et al. have reported the application of the photo-sensitive melting properties of AuNPs in controlling the novel RNA interference process via their binding with siRNAs.²⁰ Such control machinery may be better understood when the binding mechanism of the nucleic acid molecules to AuNPs is studied at the electronic level.

It is well known that bulk gold is inert and biomolecules show very low adsorption on its surface. To determine what it is in AuNPs that is responsible for the stability of these complexes, investigation of the nature of these interactions is essential for understanding the physisorption/chemisorption regime, which modulates the transport, catalytic and sensing mechanisms of these complexes. A plethora of literature is directed towards understanding the alteration in the photochemical properties of nucleic acids on being tagged with gold clusters.^21–24 Most of them have focused on understanding the influence of metal complexation on the hydrogen bonding patterns of the canonical base pairs. Kryachko et al. have reported that the interaction between DNA bases and gold clusters occurs via the N and O atoms in the bases and one gold atom.²¹ They have also shown that this interaction could be further fortified by ‘non-conventional’ NH⋯Au bonds. In another work carried out by the same group on DNA–Au complexes, the authors compared the geometrical parameters, vibrational frequencies and nuclear magnetic resonance (NMR) signatures of the NH⋯Au bonding with the prerequisites of conventional weak hydrogen bonds to substantiate their finding of the presence of ‘non-conventional’ hydrogen bonds in these complexes.²⁵ Recently, an experimental work carried out by Cao et al. on nucleobase–gold complexes using anion photoelectron spectroscopy supported by density functional theory (DFT) calculations also confirmed the existence of NH⋯Au hydrogen bonds.²⁶ Our recent studies on nucleobase–gold interactions also confirm the presence of NH⋯Au bonds via NBO studies.²⁷

In spite of the wide applications of AuNP-tagged DNA systems, their inherently low thermal stability does not allow us to achieve the long standing goal of designing a genetic system with a greater capacity of storing and transmitting information than that of natural DNA.²⁸ Designing synthetic analogues of natural DNA bases, such as size-expanded DNA bases, may possibly realize more thermally stable molecular wires. This suggests a way to go beyond the limits of natural DNA in nanotechnological applications and might eventually lead to entirely new genetic systems.^{22–24,29–33} Kool et al. synthesized size-expanded oligomers of DNA which are known to possess high thermal stability due to better stacking interactions when compared to native DNA base pairs.^28,31 Both theoretical and experimental studies suggest that, owing to larger base size, all the pairs of this helical system are fluorescent, which suggests practical applications in the detection of natural DNA and RNA using imaging techniques.^{28,31,34–36} Recent studies show that modified bases possess significantly divergent photophysical and photochemical properties, although the basic structural and bonding aspects remain the same.³⁷ This is driven by the presence of an aromatic ring that causes an alteration of the electronic distribution over the frontier molecular orbitals, thereby causing the optical response diverge from that of natural bases.³⁸ Some theoretical reports address the interaction of these size-expanded bases and base pairs with small metal clusters. Brancolini et al. have studied the interaction of size-expanded bases with copper and silver metal atoms and suggest that these complexes can be the most promising candidates for nanowires with enhanced electron transfer and also for the modification of the DNA double-helix for signal detection.²³ The binding of gold nanoclusters with size-expanded bases has also been studied, indicating a modification of electronic structure that leads to some interesting properties, such as high conductivity and charge transfer.^39,40 The interaction between size-expanded guanine and small gold clusters has been investigated, the results of which suggest that the introduction of an aromatic ring in guanine reduces the HOMO–LUMO gap and delocalizes the spatial distribution of electrons, making it ideal for charge transfer.^41,42

Previous studies have reported the interaction of DNA base pairs with metal atoms and clusters; however, the structural and electronic perturbations induced due to size-expansion in addition to metal binding has not been examined in a systematic manner. Size-expansion may lead to exciting new physico-chemical properties, like reduced HOMO–LUMO gaps, and increased dipole moments and polarizability values, which may be useful in designing improvised nano-electronic devices. Tagging to gold clusters is known to reduce the cytotoxicity of a drug/biomolecule, which can be theoretically accounted for in terms of its electrophilicity index.⁴³ In this work, we investigate the effect of adsorption of natural and size-expanded base pairs on an Au₃ gold cluster on the electronic properties of the system, using DFT. Our study focuses on how the use of size-expanded bases (Fig. 1) and gold nanoclusters alters the electronic properties and hydrogen bonding patterns of the natural base pairs, justifying the suitability of the newly designed complexes for molecular conduction applications.

Fig. 1 Optimized geometries of the size-expanded bases synthesized by Kool et al.²⁸

2 Methods

The initial structures of the DNA base pairs were generated using the GaussView05 program.⁴⁴ The coordinates of the size-expanded DNA base pairs were extracted from the NMR models of xDNA deposited in the Protein Data Bank (PDB ID: 2ICZ).⁴⁵ It has been shown that small-sized atomic clusters successfully capture the basic mechanism involved in molecular adsorption on metal surfaces, thus making our choice of an Au₃ cluster as a model for an Au(111) surface apt.⁴⁶ In order to model the base pairs, both natural and size-expanded, the sugar–phosphate backbone of these structures that was originally present was replaced with a methyl group in order to reduce the computational cost without significantly affecting the properties of the real systems, justifying the truncation being deemed accurate.⁴⁷

A benchmark study of Wu et al. performed on transition elements suggests that PBE0, which is the generalized-gradient-approximation exchange–correlation functional of Perdew, Burke, and Ernzerhof,^48–50 reproduces the experimental value of the dissociation energy,⁵¹ which is also supported in another work by Zhao and Truhlar.^52,53 In yet another work, Knal et al. have shown PBE0 to be the best method for describing the ground state thermodynamic stabilities of intermolecular charge transfer complexes.⁵⁴ Therefore, all the calculations reported in this paper were done using the PBE0 functional. Stuttgart–Dresden 19-electron effective core potentials (ECPs), designated as SDD, were used for gold.^55–58 These energy-consistent ECPs work within the relativistic Dirac–Fock theory and significantly remove the spin contamination. A split valence double-ζ augmented with a d-type polarization function for all non-hydrogen atoms and a p-type polarization function for hydrogen atoms, including an s–p and a p–d diffusion function, 6-311++G(2d,2p), was used as a basis set for the bases.^59–62 The initial geometries of the complexes were generated by placing the gold cluster at the electronegative sites of the base and were subjected to further optimization. Hence, the interaction was studied for the N3 and N7 sites of purines/x-purines and the O2 site of pyrimidines/x-pyrimidines. All possible orientations of the gold cluster (Au₃) with respect to the base pair at above mentioned titratable sites were considered, which resulted in more than one stationary point. Vibrational frequency analysis was carried out to check if all the optimized structures were at minima. Real frequencies were obtained for all the optimized structures, indicating that all the stationary points reported here are minima on the respective potential energy surfaces. The interaction energies (E_int) reported are zero-point vibrational energy (ZPVE) corrected. Details of the E_int calculations are available in the ESI.†

Analysis of charge distribution was carried out based on (i) electrostatic potential (ESP) surfaces (mapped with the total electron density) and (ii) natural population analysis (NPA). NBO analysis⁶³ was performed on these complexes to examine all possible stabilizing interactions. All the calculations were performed using the Gaussian 09 suite of programs.⁶⁴ AIM analysis was performed with the AIMAll package⁶⁵ to calculate the properties of the bond critical points (BCPs).

3 Results

3.1 Energetics

The different geometries of the complexes have been considered by placing the gold cluster at different active sites of the base pair (electron rich sites) lying on the Hoogsteen and sugar edges (Fig. 2). The major sites by which the anchoring bonds are formed in the case of AT/A–xT/xA–T systems are the N3 and N7 sites of adenine/x-adenine and O2 site of thymine/x-thymine. Similarly, in the case of GC/xGC/GxC, the N3 and N7 sites of guanine/x-guanine and the O2 site of cytosine/x-cytosine have been considered in order to study the interactions with the gold cluster.

Fig. 2 Optimized geometries of all the complexes obtained at the PBE0/SDD∪6-311++G(2d,2p) level of theory. The numbers represent the bond lengths in Å. The bond lengths in red correspond to the anchor bond. The hydrogen bonds are represented with dotted lines.

Table 1 gives the interaction energy values for all the complexes whose optimized geometries are shown in Fig. 2. It is observed that the size-expanded base pairs show better interactions with the gold cluster compared to the natural/canonical Watson–Crick (WC) base pairs. In particular, when Au₃ interacts with size-expanded pyrimidines (xT and xC) via the O(2) site, the interaction energy is increased by ∼6 kcal mol⁻¹ as a result of an additional N–H⋯Au bond. Similarly, an increase of ∼5 kcal mol⁻¹ is observed in the case of xA–T (N3) relative to A–T (N3). The highest interaction energy is found for xG–C complexes with gold. Among the various sites of interaction, in all cases we find that the N7 site of purine has the maximum affinity towards gold binding. This is also reflected in the geometrical data, where the anchoring bond length is the shortest for this particular site. In all cases, binding to the O2 site of thymine and cytosine shows minimum interaction. This may be explained on the basis of the poor electron-donating potential of the carbonyl oxygen compared to N. We also observe a nonplanar geometry corresponding to this particular interaction. This is because the gold cluster interacts with the π cloud of the C=O bond rather than the lone pairs of the oxygen, which was also found in our previous work.²⁷

Table 1 (i) Interaction energy, (ii) deformation energy of the base pair and cluster and (iii) HOMO–LUMO (H–L) gaps of all the complexes. The interaction energies and deformation energies are in kcal mol⁻¹. The H–L gaps are given in eV. All calculations have been performed at the PBE0 level of theory using the 6-311++G(2d,2p)∪SDD basis set

System	Site of interaction	Eint	E^base pairdef	E^clusterdef	H–L (isolated)	H–L (complexed)
AT	N3	−29.68	1.28	0.24	5.16	2.62
	N7	−31.35	1.22	0.35	5.16	2.68
	O2(T)	−15.45	1.36	0.07	5.16	2.27
A–xT	N3	−28.91	1.26	0.52	4.76	2.55
	N7	−31.39	1.27	0.27	4.76	2.70
	O2(T)	−21.42	1.91	0.08	4.76	2.49
xA–T	N3	−34.22	0.97	0.08	4.51	2.24
	N7	−32.35	0.89	0.06	4.51	2.43
	O2(T)	−16.80	1.37	0.07	4.51	2.27
GC	N3	−30.29	1.85	0.21	4.24	2.70
	N7	−32.86	0.90	0.19	4.24	2.23
	O2(C)	−16.78	1.86	0.08	4.24	2.29
G–xC	N3	−30.16	1.86	0.23	3.76	2.42
	N7	−32.89	0.92	0.20	3.76	1.90
	O2(C)	−22.11	2.20	0.10	3.76	2.51
xG–C	N3	−32.31	1.43	0.25	4.08	2.70
	N7	−35.48	0.93	0.22	4.08	2.39
	O2(C)	−16.68	1.88	0.07	4.08	2.30

---

The deformation energies (details of calculation available in the ESI†) of the base pair and the gold cluster occurring due to complexation were also calculated to give a quantitative insight into the instability arising in each of the monomers due to the complex formation. The values for the cluster suggest that very little deformation occurs on interaction with the base pair. This indicates that adsorption of the base pair on gold surface would not cause major alteration in the lattice structure of the AuNP. The deformation energy corresponding to the base pair lies in the range of 0.89–1.91 kcal mol⁻¹. A careful observation of Table 1 suggests that the lower the deformation energy of the base-pair, the higher the corresponding interaction energy, which suggests that the stability of the base pair also plays an important role in enhancing the affinity towards the gold cluster. For example, GC has three possible sites interacting with Au₃ that result in different deformation energy values, and amongst them N7 shows the minimum deformation energy value of 0.90 kcal mol⁻¹. This particular complex shows the maximum interaction energy value with Au₃.

3.2 Nature of the anchoring bond

It is evident by now that structural perturbations give rise to a certain pattern in energetics. We now attempt to explain this on the basis of (i) the nature of the anchoring bond and position of the gold cluster and (ii) the strength of the inter-base hydrogen bonds.

The anchoring bond lengths are referred to as the bond length between the gold atom (acceptor) directly interacting with the active site of the base (donor). The anchor and nonconventional N–H⋯Au hydrogen bonds are considered to be the two major factors that govern the hybridization between the nucleobases and gold clusters, as reported in some earlier works.^21,25,27 This causes the electron density of the nucleobases to change, particularly at the sites which are involved in the intermolecular H-bonds with the WC complementary ones, which was also predicted in our earlier work on base–gold interactions.²⁷

In all cases, the interaction with the N7 site exhibits the shortest bond length. This suggests that the N7 site has the highest affinity for gold, an observation in line with previous results.²⁵ This may be due to the easily available lone pair of electrons on the nitrogen. The nitrogen here is sp² hybridised and hence has a higher electron donating capacity than any other site considered. The N3 site of purines lying on the sugar edge have longer anchor bond lengths (by 0.02 Å) when compared to the N7 site, even though they are also sp² hybridised. This may be explained on the basis of the steric hindrance provided by the methyl group present on the adjacent N9 position. It is also observed that the interaction with the gold cluster is non-planar wherever the carbonyl oxygen is involved in the interaction, as discussed above.

The introduction of a spacer ring is also responsible for altering the anchoring bonds and reducing the bond lengths by around 0.01 Å. In the case of the N3 site, the spacer ring is also responsible for reducing the steric hindrance caused by the methyl group. For the O2 site, the effect is even more prominent. The planarity of the complex is regained on the insertion of a spacer ring into the corresponding base (A–xT (O2),G–xC (O2)). This structural perturbation is additionally stabilized by the formation of a ‘non-conventional’ C/N–H⋯Au bond.

The results of natural bond orbital (NBO) analysis and the shapes of the frontier molecular orbitals (Fig. 4 and 5) indicate that the anchoring bond is obtained by charge transfer from the N or O lone pair to the antibonding orbital of gold (Table S5 of the ESI†). Also, the ‘non-conventional’ N–H⋯Au bonds are characterized by charge transfer from the LP of gold to the BD* orbital of the NH groups. The detailed perturbation theory energy analysis is reported in the ESI (Table S5†). In addition to this, the nature of the bonding present in the formation of the anchoring bond is studied using AIM parameters. Table 2 indicates a positive ∇²ρ(r) in all cases, supporting the existence of ionic interactions in the formation of the anchoring bonds. In contrast, Table 2 also indicates negative values for H(r) in all cases, which supports the covalent character of these bonds. From this it can be concluded that the anchoring bonds are partially ionic and partially covalent in nature. For complexes with a non-planar geometry and lower interaction energy, the value of H(r) is also less, suggesting H(r) to be an indicator of complex stability.

Table 2 Bond critical point data (in atomic units) for the anchoring bond from AIM analysis carried out at the PBE0 level of theory using the 6-311++G(2d,2p)∪SDD basis set. See ESI for more details

System	Site of interaction	∇^2ρ(r)	G(r)	V(r)	H(r)
AT	N3	3.72 × 10^−1	1.23 × 10^−1	−1.53 × 10^−1	−3.01 × 10^−2
	N7	3.88 × 10^−1	1.30 × 10^−1	−1.63 × 10^−1	−3.32 × 10^−2
	O2(T)	3.27 × 10^−1	8.91 × 10^−2	−9.65 × 10^−2	−7.42 × 10^−3
A–xT	N3	3.66 × 10^−1	1.21 × 10^−1	−1.50 × 10^−1	−2.93 × 10^−2
	N7	4.09 × 10^−1	1.31 × 10^−1	−1.59 × 10^−1	−2.85 × 10^−2
	O2(T)	3.70 × 10^−1	1.04 × 10^−1	−1.14 × 10^−1	−1.10 × 10^−2
xA–T	N3	3.64 × 10^−1	1.21 × 10^−1	−1.51 × 10^−1	−3.02 × 10^−2
	N7	3.90 × 10^−1	1.30 × 10^−1	−1.63 × 10^−1	−3.29 × 10^−2
	O2(T)	3.25 × 10^−1	8.86 × 10^−2	−9.60 × 10^−2	−7.38 × 10^−3
GC	N3	3.58 × 10^−1	1.19 × 10^−1	−1.49 × 10^−1	−2.98 × 10^−2
	N7	4.05 × 10^−1	1.28 × 10^−1	−1.55 × 10^−1	−2.69 × 10^−2
	O2(C)	3.31 × 10^−1	9.11 × 10^−2	−9.95 × 10^−2	−8.40 × 10^−3
G–xC	N3	3.58 × 10^−1	1.19 × 10^−1	−1.49 × 10^−1	−2.98 × 10^−2
	N7	3.85 × 10^−1	1.28 × 10^−1	−1.59 × 10^−1	−3.15 × 10^−2
	O2(C)	3.80 × 10^−1	1.07 × 10^−1	−1.19 × 10^−1	−1.22 × 10^−2
xG–C	N3	3.55 × 10^−1	1.19 × 10^−1	−1.50 × 10^−1	−3.07 × 10^−2
	N7	4.09 × 10^−1	1.31 × 10^−1	−1.59 × 10^−1	−2.84 × 10^−2
	O2(C)	3.29 × 10^−1	9.06 × 10^−2	−9.90 × 10^−2	−8.35 × 10^−3

---

3.3 Effect of Au₃ interaction on base pairing

A charge redistribution is observed along the WC edge of the interaction (Table S3 of ESI†), suggesting an alteration in the hydrogen bonding pattern of the base pair. The geometry and frequency analysis is carried out to further substantiate this prediction. Hydrogen bonding strength can be predicted on the basis of the change in bond length and bond angles and is based on the red/blue shift observed in the vibrational stretching frequency of the bond involved in the hydrogen bond formation.^21,66,67 For the interaction at the N3 site, the distance between the donor and acceptor groups, i.e. A(N6)–T(O4), is reduced and the corresponding bond angle is increased in the case of A–T and A–xT. The corresponding N–H stretching frequency is also red-shifted (−63.47 cm⁻¹) relative to the uncomplexed base pair, indicating a strengthening of the A(N6)–T(O4) hydrogen bond. In the case of the xA–T complex, the bond becomes more linear, but the donor acceptor distance is increased by 0.023 Å, with a blue shift of 137.72 cm⁻¹. The data in Table 3 indicates a weakening of the A(N1)–T(N3) hydrogen bond in all these cases, which is further substantiated by a reduction in the E(2) value (by 3–4 kcal mol⁻¹, Table S5 of ESI†). The N7 site of interaction does not show much effect on the hydrogen bonding patterns in the case of the xA–T complex. In the other two cases, the A(N6)–T(O4) bond is more linear with respect to the untagged base pair, with a red shift in the corresponding hydrogen bond, indicating a stronger interaction. In all cases, the geometries obtained after optimization for the interaction with the O2 site of thymine are non-planar, i.e., the gold cluster and the base pair do not lie in the same plane. In all these cases, there is a reduction in the hydrogen bonding angle between A(N6)–T(O4), an increase in the bond length and a blue shift in the vibrational frequency, all indicating a weakening of the corresponding bond (Table 3), which is further supported by a reduction in the E(2) value of the respective hydrogen bonding interaction. Thus, it appears that for the interaction with the gold cluster from the Hoogsteen edge of adenine (N7), the AT base pair may facilitate a slight opening of the hydrogen bond from the major groove site. In the other two cases (A–xT and xA–T), the opening of the hydrogen bond is predicted to be facilitated from the minor groove side. When the cluster interacts with the sugar edge of adenine (N3), the base pair opening is facilitated from the minor groove for all three base pairs. When the cluster is interacting in a non-planar fashion (interaction with the O2 site), the hydrogen bond opening is expected from the major groove site in all complexes.

Table 3 The changes in hydrogen bonding length (Δr, in Å), angles (in degrees), and stretching frequency (Δν, in cm⁻¹) of the AT base pairs before and after complexation have been shown. All the complexes have been optimized at the PBE0 level of theory using the 6-311++G(2d,2p)∪SDD basis set^a

System	Site of interaction	Atoms	Δr*	Δ∠*	Δν*
a Δr* = rcomplex − risolated, Δ∠* = ∠complex − ∠isolated, Δν* = νcomplex − νisolated.
AT	N3	A(N1)–T(N3)	0.04	−0.9	199.5
		A(N6)–T(O4)	−0.04	1.8	−63.5
		A(C2)–T(O2)	0.03	−2.4	22.7
	N7	A(N1)–T(N3)	−0.03	−0.8	123.8
		A(N6)–T(O4)	0.05	2.0	−56.0
		A(C2)–T(O2)	0.03	0.9	0.7
	O2(T)	A(N1)–T(N3)	−0.11	0.4	−233.1
		A(N6)–T(O4)	0.07	−1.5	38.2
		A(C2)–T(O2)	0.10	0.0	3.9
A–xT	N3	A(N1)–T(N3)	0.04	−0.5	180.4
		A(N6)–T(O4)	−0.03	1.7	−68.8
		A(C2)–T(O2)	0.00	−2.2	21.4
	N7	A(N1)–T(N3)	0.03	−0.6	114.7
		A(N6)–T(O4)	0.00	2.1	−53.2
		A(C2)–T(O2)	0.01	1.3	−11.8
	O2(T)	A(N1)–T(N3)	−0.04	0.4	−192.0
		A(N6)–T(O4)	0.00	−1.4	25.0
		A(C2)–T(O2)	−0.12	−0.2	5.2
xA–T	N3	A(N1)–T(N3)	0.02	−0.9	137.7
		A(N6)–T(O4)	0.02	2.0	0.8
		A(C2)–T(O2)	0.05	−2.1	1.7
	N7	A(N1)–T(N3)	0.02	−0.8	67.5
		A(N6)–T(O4)	−0.02	0.2	−26.4
		A(C2)–T(O2)	0.05	−0.5	−12.1
	O2(T)	A(N1)–T(N3)	−0.04	0.2	−242.6
		A(N6)–T(O4)	0.01	−1.3	37.2
		A(C2)–T(O2)	−0.10	−0.1	3.2

---

The hydrogen bonding patterns in the G–C counterparts are also similarly affected, owing to tagging with the gold cluster (Table 4). When the cluster interacts from the N3 site of G–C, the G(N1)–C(N3) and G(N2)–C(O2) bond distances are reduced, whereas the G(O6)–C(N4) bond distance is increased (Table 4). The complexes with xG–C also follow the same pattern. In the case of the complex with G–xC, there is a slight lengthening in the G(N1)–C(N3) bond by only 0.004 Å. Vibrational frequency analysis suggests a weakening of the hydrogen bond strength in the G–C base pair, where as in G–xC the bonds are expected to be stronger, which is also supported by the NBO data (Table S5 of the ESI†). In the case of xG–C, the G(N1)–C(N3) bond is weakened, whereas the other two bonds become more linear. The interaction with the N7 site causes a lengthening of the G(O6)–C(N4) bond and a shortening of the other two bonds in all three cases. The vibrational frequency analysis suggests that the hydrogen bonds are weakened in the case of G–C, and strengthened in the case of G–xC. The G(O6)–C(N4) bond is weakened in the case of xG–C and the other two bonds are strengthened. The interaction with the O2 site causes the shortening of the G(O6)–C(N4) bond and the lengthening of the other two bonds in all three complexes. The angles are reduced in their linearity in all three hydrogen bonds. This analysis suggests that tagging the gold at the N3 or N7 site of guanine would facilitate the base-pair opening from the major groove, whereas the same would be favored from the minor groove if the gold is tagged to the O2 site of cytosine. A comparison of the hydrogen bonding data obtained via NBO calculations for the natural and modified (size-expanded and tagged with gold) base pairs also suggests the weakening of these bonds, resulting in their opening from the major groove if the cluster is tagged at the purines/x-purines (Table S5 of the ESI†). The opening is facilitated from the minor groove if the cluster is tagged to the pyrimidines/x-pyrimidines. A comparison of the BCP parameters for the hydrogen bonds present in the (un)complexed base pairs also indicates that the opening of the base pair is site-specific, i.e. it can be controlled by varying the site with which the gold cluster interacts. The details of these calculations are provided in Table S6 of the ESI.† This site-specific behavior of the alteration in hydrogen bonding patterns is a useful tool for tailoring the unwinding of DNA strands.

Table 4 The changes in hydrogen bonding length (Δr, in Å), angles (in degrees), and stretching frequency (Δν, in cm⁻¹) of the GC base pairs before and after complexation have been shown. All the complexes have been optimized at the PBE0 level of theory using the 6-311++G(2d,2p)∪SDD basis set^a

System	Site of interaction	Atoms	Δr*	Δ∠*	Δν*
a Δr* = rcomplex − risolated, Δ∠* = ∠complex − ∠isolated, Δν* = νcomplex − νisolated.
GC	N3	G(O6)–C(N4)	0.03	−2.1	113.2
		G(N1)–C(N3)	−0.02	−0.7	−109.1
		G(N2)–C(O2)	−0.07	−0.8	−106.8
	N7	G(O6)–C(N4)	0.03	−2.1	131.7
		G(N1)–C(N3)	−0.03	−0.9	−110.9
		G(N2)–C(O2)	−0.04	−1.1	−51.6
	O2(C)	G(O6)–C(N4)	−0.04	−1.2	−83.4
		G(N1)–C(N3)	0.05	−2.1	92.1
		G(N2)–C(O2)	0.13	−3.2	123.2
G–xC	N3	G(O6)–C(N4)	0.03	0.8	131.5
		G(N1)–C(N3)	0.00	0.2	−96.5
		G(N2)–C(O2)	−0.08	1.1	−67.1
	N7	G(O6)–C(N4)	0.04	1.3	119.5
		G(N1)–C(N3)	0.00	0.5	−106.6
		G(N2)–C(O2)	−0.05	0.8	−116.0
	O2(C)	G(O6)–C(N4)	−0.03	−1.4	−63.9
		G(N1)–C(N3)	0.08	−1.2	86.5
		G(N2)–C(O2)	0.10	−2.6	133.8
xG–C	N3	G(O6)–C(N4)	0.02	−1.5	41.7
		G(N1)–C(N3)	−0.02	0.5	−89.3
		G(N2)–C(O2)	−0.08	2.8	−31.3
	N7	G(O6)–C(N4)	0.02	−0.7	57.7
		G(N1)–C(N3)	−0.01	0.6	−113.3
		G(N2)–C(O2)	−0.04	1.7	−106.3
	O2(C)	G(O6)–C(N4)	−0.04	0.1	−116.7
		G(N1)–C(N3)	0.06	−1.2	85.9
		G(N2)–C(O2)	0.12	−2.2	107.7

---

3.4 Modulation of electronic properties

It would be interesting to see how structural perturbations affect the electronic properties, which can be quantified in terms of H–L gaps, dipole moment and polarizability values. The frontier orbitals play an important role in defining the molecular properties of a system and the H–L gaps are a quantitative measure of the reactivity/stability of a system. It is interesting to note that the canonical AT base pair has a lower H–L gap compared to GC (Table 1). However, Fig. 3 shows that both size expansion and complexation with a gold cluster reduce the H–L gap. A relative decrease in the gaps is observed on ring expansion (Fig. 3) owing to the extended π delocalization. The influence of size expansion on H–L gap is different in AT and GC systems. Using a size-expanded adenine coupled to thymine brings down the gap more (4.51 eV) than when size-expanded thymine is coupled to adenine (4.76 eV), in contrast to what we observe in the case of GC (Fig. 3). The values clearly indicate a sharp decrease in the HOMO–LUMO gaps on complexation with the cluster. The decrease in gaps is system- as well as site-specific. The alteration of the HOMO and LUMO orbitals of the base pair owing to structural perturbations is probably the cause of this marked reduction in the gap. The HOMO−1, HOMO, LUMO and LUMO+1 natural orbitals of the complexed and isolated base pairs are plotted in Fig. 4 and 5. In all the isolated base pairs, the HOMO has a π character and lies over the purine/x-purine. The LUMO is also found to possess a π character, but lies over the corresponding pyrimidine/x-pyrimidine. In all complexes, it is observed that the HOMO is shifted to the metal cluster, which is in line with some of the earlier reported results.^27,34 The LUMO is mainly located on the metal cluster with a small participation of the molecular orbital of the atom with which the anchoring bond is formed. This suggests that under conditions of pH stress, the metal cluster would protect the base pair from any further electronic or structural perturbations and thus can be used for designing materials that are subjected to these conditions. From Fig. 4 and 5, it is clear that this interaction also alters the HOMO−1 and LUMO+1 orbitals. Thus, we can conclude that complexation causes an alteration in the frontier molecular orbitals, which in turn causes the HOMO–LUMO gaps to decrease. This feature may be exploited to enhance the capability for transporting mobile charges in view of nanoelectronic applications.

Fig. 3 Variation in HOMO–LUMO gaps of base pairs on complexation.

Fig. 4 The distribution of the HOMO−1, HOMO, LUMO and LUMO+1 levels of the complexed and uncomplexed AT base pairs, calculated at the UHF level of theory using the 6-31+G(2d,2p)∪SDD basis set.

Fig. 5 The distribution of the HOMO−1, HOMO, LUMO and LUMO+1 levels of the complexed and uncomplexed GC base pairs calculated at the UHF level of theory using the 6-31+G(2d,2p)∪SDD basis set.

The dipole moments (μ) and polarizabilities (α) were computed in order to examine the effect of complexation on the electronic properties of the base pairs. The values are available in Table S4 of the ESI.† The dipole moment is higher for GC than for AT. It is observed that μ varies on ring expansion (Fig. 6). Pairing a size-expanded pyrimidine with a purine causes the dipole moment to increase, whereas the opposite happens when size-expanded purines are paired with pyrimidines. Tagging with the gold cluster causes the dipole moment to increase in all cases, except when G–C and its variants are made to interact with the cluster from the O2 site of cytosine. Fig. 7 clearly shows an increase in the value of polarizability (α) on ring expansion in all cases. This value is further raised on tagging the base pair with the gold cluster. It is found that size-expanded purines tagged with the cluster at the N7 site show the maximum value of polarizability in both xA–T and xG–C base pairs. The increase in polarizability causes the dispersion forces to increase, resulting in an increase in the melting and boiling points of the complex.⁶⁸ Hence, we can expect that these structural perturbations lead to the formation of more thermally stable complexes that find a more relevant place in the design of nanoelectronic devices.

Fig. 6 Variation in dipole moment (μ) values of base pairs on complexation.

Fig. 7 Variation in polarizability (α) values of base pairs on complexation.

It has been reported that the global electrophilic power of a molecule can be quantified in terms of a global electrophilicity index (ω).⁶⁹ The value of ω gives a measure of the propensity of the molecule to act as a nucleophile. It is known from previous studies that DNA acts as a nucleophile and tends to attack certain water-soluble epoxides that are carcinogenic.⁷⁰ This results in the complexation of DNA with these molecules, causing damage to the DNA. The increase in the electrophilicity index values suggests that the tendency to react with epoxides would possibly decrease. The values of ω for the complexed systems are reported. It is clear from Fig. 8 that the electrophilicity index values increase on size-expansion, which is further enhanced by complexation. The enhancement in this value is dependent on the site with which the gold interacts. However, in both cases (AT and GC) it is observed that the ω value is at its maximum when the interaction is taking place with the O2 site. This information is useful in producing drugs that have a high degree of selectivity and specificity.

Fig. 8 Variation in electrophilicity index (ω) values of base pairs on complexation.

3.5 Binding site-specific charge redistribution

Electron transfer processes can be studied by visualizing the electron density difference, namely the total charge density of the complex minus the electron density of the gold cluster and the base pair in their standalone states. This is shown in Fig. 9 and Fig. 10 for the AT and GC complexes, along with their variants. The NPA analysis of the donor and acceptor atoms in the base pair and complex suggest an alteration in the hydrogen bonding patterns owing to ring expansion and tagging with the gold cluster. It can be seen that, owing to these structural perturbations, a charge redistribution takes place along the Hoogsteen and sugar edges that can possibly favor higher order interactions. This is an important property in terms of designing novel molecular wires. It is noticed that when the gold cluster is placed at the N3 site of a purine/x-purine base, the charge distribution around the Hoogsteen edge undergoes an enormous change (from 0.2 to 0.7 a.u.), whereas the placement of the cluster at the N7 site affects the charge distribution at the sugar edge (see Table S3 of the ESI† for details). The complexation with the O2 site of pyrimidines/x-pyrimidines does not cause a significant change in charge distribution along either of the edges. Hence, we can modulate the behavior at the edges of the base pair by selectively placing the gold cluster.

Fig. 9 Electrostatic potential surface mapped over isodensity surface for complexed and uncomplexed (un)modified AT base pairs in the gas phase. The isovalue for these images is 0.0004 a.u. Δq_cluster refers to the amount of charge transferred to the neutral gold cluster on complexation.

Fig. 10 Electrostatic potential surface mapped over isodensity surface for complexed and uncomplexed (un)modified GC base pairs in the gas phase. The isovalue for these images is 0.0004 a.u. Δq_cluster refers to the amount of charge transferred to the neutral gold cluster on complexation.

4 Conclusion

In this work, density functional theory has been applied in order to explore the alteration in geometries, electronic structures, charge populations and interaction energies of DNA base pairs on ring expansion and tagging with an Au₃ cluster. The calculations show that gold nanoclusters form stable complexes with natural as well as size-expanded base pairs, with a higher affinity shown by size-expanded base pairs. It is evident from our results that the nature of the N/O–Au bonds is partially covalent and partially ionic, with the lone pair electrons of the O and N atoms being transferred to the antibonding orbitals of gold. This binding is fortified by the ‘non-conventional’ NH⋯Au hydrogen bonds. This interaction seems to play an important role in stabilizing the DNA molecule over AuNPs. The natural orbital picture shows that the frontier orbitals lie on the gold, indicating the potential of the cluster to protect the DNA under conditions of chemical stress.

The structural perturbations introduced induce a base pair distortion which is found to be binding site-specific. This feature can be exploited in designing highly selective and specific nano-devices. Following the gold binding, a redistribution of electronic charge around the Hoogsteen and sugar edges takes place, suggesting that these systems favor higher order interactions. This distinctive property may provide a promising scaffold for the synthesis of 3D metalized objects that find application in nano-electronics.

The electronic coupling between the metal atoms and nucleic acid base pairs results in the reduction of the HOMO–LUMO gaps, suggesting that these systems might behave as good conductors. It is also found that on complexation, a considerable amount of electronic charge is transferred from the base pair to the gold cluster. Thus, the gold clusters oxidize the base/x-base. The increase in α values indicates greater thermal stability. Increasing ω values emphasizes the importance of these systems in designing drugs related to curing cancer. Hence, it can be concluded that an alteration in geometric and electronic properties on tagging the base pairs with gold clusters opens up an avenue for developing novel nano-bioelectronic devices/sensors with tailored molecular properties.

Acknowledgements

We thank the Department of Science and Technology for financial support. S. R. acknowledges support from the CSIR for SRF fellowship.

References

1. R. Jin, Y. Cao, C. A. Mirkin, K. L. Kelly, G. C. Schatz and J. G. Zheng, Science, 2001, 294, 1901–1903.
2. C. A. Mirkin, R. L. Letsinger, R. C. Mucic and J. J. Storhoff, Nature, 1996, 382, 607–609.
3. Y. Chen, H. Wu, Z. Li, P. Wang, L. Yang and Y. Fang, Plasmonics, 2012, 7, 509–513.
4. S. J. Oldenburg, J. B. Jackson, S. L. Westcott and N. J. Halas, Appl. Phys. Lett., 1999, 75, 2897–2899.
5. G. S. Shafai, S. Shetty, S. Krishnamurty, V. Shah and D. G. Kanhere, J. Chem. Phys., 2007, 126, 014704–014712.
6. M. Haruta, T. Kobayashi, H. Sano and N. Yamada, Chem. Lett., 1987, 16, 405–408.
7. R. K. DeLong, C. M. Reynolds, Y. Malcolm, A. Schaeffer, T. Severs and A. Wanekaya, Nanotechnol., Sci. Appl., 2010, 3, 53–63.
8. T. H. Lee and K. M. Ervin, J. Phys. Chem., 1994, 98, 10023–10031.
9. I. L. Garzón, C. Rovira, K. Michaelian, M. R. Beltrán, P. Ordejón, J. Junquera, D. Sánchez-Portal, E. Artacho and J. M. Soler, Phys. Rev. Lett., 2000, 85, 5250–5251.
10. H. Häkkinen, M. Moseler and U. Landman, Phys. Rev. Lett., 2002, 89, 033401–033404.
11. J. Yu, S. Choi, C. I. Richards, Y. Antoku and R. M. Dickson, Photochem. Photobiol., 2008, 84, 1435–1439.
12. D. Pissuwan, T. Niidome and M. B. Cortie, J. Controlled Release, 2011, 149, 65–71.
13. P. Aich, S. L. Labiuk, L. W. Tari, L. J. Delbaere, W. J. Roesler, K. J. Falk, R. P. Steer and J. S. Lee, J. Mol. Biol., 1999, 294, 477–485.
14. K. Tanaka, A. Tengeiji, T. Kato, N. Toyama and M. Shionoya, Science, 2003, 299, 1212–1213.
15. K. Tanaka, G. H. Clever, Y. Takezawa, Y. Yamada, C. Kaul, M. Shionoya and T. Carell, Nat. Nanotechnol., 2006, 1, 190–194.
16. M. H. Lee and O. F. Sankey, J. Phys.: Condens. Matter, 2009, 21, 351101–3511011.
17. R. Elghanian, J. J. Storhoff, R. C. Mucic, R. L. Letsinger and C. A. Mirkin, Science, 1997, 277, 1078–1081.
18. R. Shenhar and V. M. Rotello, Acc. Chem. Res., 2003, 36, 549–561.
19. J. Cheon and J.-H. Lee, Acc. Chem. Res., 2008, 41, 1630–1640.
20. Y. Matsushita-Ishiodori and T. Ohtsuki, Acc. Chem. Res., 2012, 45, 1039–1047.
21. E. S. Kryachko and F. Remacle, Nano Lett., 2005, 5, 735–739.
22. D. Porath, G. Cuniberti and R. Felice, Charge Transport in DNA-Based Devices, Springer, Berlin Heidelberg, 2004, vol. 237, pp. 183–228.
23. G. Brancolini and R. D. Felice, J. Chem. Phys., 2011, 134, 205102–205114.
24. M. Nagatori, M. Ojima, Y. Ibuki, H. Sakamoto and K. Mizoguchi, J. Phys. Soc. Jpn., 2011, 80, 114803–114808.
25. E. S. Kryachko and F. Remacle, J. Phys. Chem. B, 2005, 109, 22746–22757.
26. G.-J. Cao, H.-G. Xu, R.-Z. Li and W. Zheng, J. Chem. Phys., 2012, 136, 014305–014308.
27. S. Rai, S. Ranjan, H. Singh and U. D. Priyakumar, RSC Adv., 2014, 4, 29642–29651.
28. S. R. Lynch, H. Liu, J. Gao and E. T. Kool, J. Am. Chem. Soc., 2006, 128, 14704–14711.
29. C. Brotschi and C. J. Leumann, Angew. Chem., Int. Ed., 2003, 42, 1655–1658.
30. M. Kaufmann, M. Gisler and C. Leumann, Angew. Chem., Int. Ed., 2009, 48, 3810–3813.
31. H. Liu, J. Gao, S. R. Lynch, Y. D. Saito, L. Maynard and E. T. Kool, Science, 2003, 302, 868–871.
32. D. W. Kang, X. P. Hao, X. Z. Li, L. B. Li and S. J. Xie, Appl. Phys. Lett., 2013, 102, 072410.
33. M. Zwolak and M. D. Ventra, Appl. Phys. Lett., 2002, 81, 925–927.
34. M. Fuentes-Cabrera, X. Zhao, P. R. C. Kent and B. G. Sumpter, J. Phys. Chem. B, 2007, 111, 9057–9061.
35. A. Migliore, S. Corni, D. Varsano, M. L. Klein and R. Di Felice, J. Phys. Chem. B, 2009, 113, 9402–9415.
36. J. R. Blas, O. Huertas, C. Tabares, B. G. Sumpter, M. Fuentes-Cabrera, M. Orozco, P. Ordejn and F. J. Luque, J. Phys. Chem. A, 2011, 115, 11344–11354.
37. P. K. Samanta and S. K. Pati, New J. Chem., 2013, 37, 3640–3646.
38. D. Varsano, A. Garbesi and R. Di Felice, J. Phys. Chem. B, 2007, 111, 14012–14021.
39. P. Sharma, S. Sharma, A. Mitra and H. Singh, J. Biomol. Struct. Dyn., 2009, 27, 65–81.
40. P. Sharma, H. Singh, S. Sharma and H. Singh, J. Chem. Theory Comput., 2007, 3, 2301–2311.
41. W. Sun and R. Di Felice, J. Phys. Chem. C, 2012, 116, 24954–24961.
42. L. Zhang, T. Ren, X. Yang, L. Zhou and X. Li, Int. J. Quantum Chem., 2013, 113, 2234–2242.
43. S. Pal, K. Mitra, S. Azmi, J. K. Ghosh and T. K. Chakraborty, Org. Biomol. Chem., 2011, 9, 4806–4810.
44. R. Dennington, T. Keith and J. Millam, GaussView Version 5, Semichem Inc., Shawnee Mission KS, 2009.
45. S. R. Lynch, H. Liu, J. Gao and E. T. Kool, J. Am. Chem. Soc., 2006, 128, 14704–14711.
46. P. J. Mohan, A. Datta, S. S. Mallajosyula and S. K. Pati, J.Phys. Chem. B, 2006, 110, 18661–18664.
47. D. Bhattacharyya, S. C. Koripella, A. Mitra, V. B. Rajendran and B. Sinha, J. Biosci., 2007, 32, 809–825.
48. E. M. Fernández, J. M. Soler, I. L. Garzón and L. C. Balbás, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 165403–165417.
49. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
50. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401–146405.
51. Z. J. Wu, J. S. Shi, S. Y. Zhang and H. J. Zhang, Phys. Rev. A: At., Mol., Opt. Phys., 2004, 69, 064502–064506.
52. Y. Zhao and D. G. Truhlar, Phys. Chem. Chem. Phys., 2005, 7, 2701–2705.
53. Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2007, 3, 289–300.
54. A. Knal and N. Acar, J. Mol. Struct.: THEOCHEM, 2010, 949, 36–40.
55. A. Ehlers, M. Bhme, S. Dapprich, A. Gobbi, A. Hllwarth, V. Jonas, K. Khler, R. Stegmann, A. Veldkamp and G. Frenking, Chem. Phys. Lett., 1993, 208, 111–114.
56. M. Dolg, U. Wedig, H. Stoll and H. Preuss, J. Chem. Phys., 1987, 86, 866–872.
57. D. Andrae, U. Huermann, M. Dolg, H. Stoll and H. Preu, Theor. Chim. Acta, 1990, 77, 123–141.
58. E. M. Fernández, J. M. Soler and L. C. Balbás, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 235433–235441.
59. P. Hariharan and J. Pople, Mol. Phys., 1974, 27, 209–214.
60. P. Hariharan and J. Pople, Chem. Phys. Lett., 1972, 16, 217–219.
61. V. A. Rassolov, M. A. Ratner, J. A. Pople, P. C. Redfern and L. A. Curtiss, J. Comput. Chem., 2001, 22, 976–984.
62. W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261.
63. E. D. Glendening, A. E. Reed, J. E. Carpenter and F. Weinhold, NBO Version 3.1, Gaussian, Inc., Wallingford, CT, 2004.
64. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision C.01, Gaussian Inc., Wallingford CT, 2009.
65. T. K. Gristmill and T. A. Keith, AIMAll (Version 12.09.23), Overland Park KS, USA, 2012.
66. S. J. Grabowski, Chem. Phys. Lett., 2001, 338, 361–366.
67. S. J. Grabowski, J. Phys. Org. Chem., 2004, 17, 18–31.
68. P. W. Atkins, Atkins’ Physical chemistry, Oxford University Press, Oxford New York, 2010.
69. R. G. Parr, L. v. Szentpály and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922–1924.
70. B. N. Ames and L. S. Gold, Mutat. Res., Fundam. Mol. Mech. Mutagen., 2000, 447, 3–13.

---

Footnote

† Electronic supplementary information (ESI) available: Geometric features, frequency analysis, discussion of dipole moments, polarizability values, electrophilicity index, NBO and AIM details. See DOI: 10.1039/c5ra04668h

---