Directly probing the effect of the solvent on a catalyst electronic environment using X-ray photoelectron spectroscopy

Abstract

The electronic environment of the metal centre of a catalyst dissolved in ionic liquids has a determining effect on its catalytic efficiency in chemical reactions. However, the electronic environment of the ionic liquid-based metal centres can be influenced by not only their chemical state but also the solute–solvent interaction. In this work, we demonstrate that the anion of an ionic liquid can significantly influence the electronic environment of a metal centre. The metal centre electronic environment can be monitored by measuring the typical electron binding energies by X-ray photoelectron spectroscopy (XPS). The correlation of the electronic environment of the metal centre with reaction performance provides a possibility to design and control a chemical reaction. In this work, we also illustrate a strategy for tuning the electronic environment of metal centres, by the selection of particular ionic liquid anions, to design a catalytic system and consequently to finally control the reaction performance of a model Suzuki cross coupling reaction.

---

Introduction

Ionic liquids are nowadays one of the options that the common chemist considers as the solvent for any particular reaction. Many reviews and books focus on their use as solvents for synthesis and catalysis.^1–5 In particular, the relatively non-volatile nature of ionic liquids can offer tremendous opportunities in terms of immobilising homogeneous catalysis, and the efficient separation of products post-reaction.^6–8 There is a growing interest in the role that ionic liquids play during chemical reactions, particularly those dependent upon homogeneous catalytic processes.^1,3,4 In many cases, the ionic liquid acts as an “innocent” solvent, particularly when the active catalyst is a neutral species.¹ However, in many cases ionic liquids can be involved in the formation of the final active metal complexes. Ionic liquids can act in these cases as the catalyst ligand, the ligand precursor, the co-catalyst or even the catalyst for a reaction.⁹ In the case of cationic metal catalysts, ionic liquids have been shown to displace the counteranion of the cationic metal centre.³ Even non-coordinating anions, such as [Tf₂N]⁻ (bis[(trifluoromethane)sulfonyl]imide), have been shown to coordinate to the metal centre of catalysts.^10,11 The coordination of the cation of the ionic liquid via the formation of a carbocation has also been widely investigated. The Suzuki cross coupling reaction is typically catalysed by tetrakis(triphenylphosphine) palladium ([Pd(PPh₃)₄]), but the formation of a phosphineimidazolylidene palladium complex has also been linked to an increase in reaction rate when carried out in imidazolium-based ionic liquid solutions.^12,13

The analysis of the catalyst in solution is of utmost importance in order to be able to understand the role of ionic liquids in homogeneous catalytic reactions. Several techniques have been used to characterise the catalyst in solution. Electrospray ionisation mass spectrometry (ESI-MS) can provide with the spectrometric evidence of the catalyst especially when charged catalyst are involved.¹⁴ Synchrotron based extended X-ray absorption fine structure (EXAFS) spectroscopy can provide the first coordination shell of the catalyst in solution and bond distances.¹⁵ IR,¹⁶ UV-vis¹⁷ and EPR¹⁸ spectra can also be used to identify its spectroscopic fingerprint in solution. One of the main factors controlling the outcome of these reactions is the electronic environment of the metal centre of the catalysts. This information can, potentially, be indirectly obtained from NMR spectroscopy of the ligand characteristic atoms and metal centre or IR spectroscopy of the metal–ligand bonds signals, or directly measured by UV-vis spectra. UV-vis and IR spectroscopy have been routinely used to assess the donating ability of ligands to metal centres. These techniques could be potentially used to observe the effect of other ligands or the existence of new ionic liquid–metal centre interactions. However, for UV-vis and IR spectroscopy, the acquisition of this information is dependent upon the catalyst producing an observable (i.e. not obscured by the ionic liquid) spectroscopic signal. For NMR spectroscopy, only diamagnetic complexes can be analysed, which in practice prevents the analysis of many systems. These are likely reasons for the scarcity of such studies in ionic liquid systems.⁹

X-ray photoelectron spectroscopy (XPS) is a powerful analytical tool that allows investigations of the bulk electronic environment of both solids and solvents/solutes. XPS of solid catalysts has been used for years to characterise the metal oxidation state. However, studies of the electronic environment of metal centres in solution have been limited by experimental challenges as most solvents are too volatile to be studied using conventional XPS apparatus.^19–22 XPS offers a unique spectroscopic opportunity to investigate the presence of solvent–solute interactions that may promote the in situ formation of new catalytic species that otherwise could not be characterised by more traditional solution-based spectroscopic methods.

Over the past decade, the use of XPS in the investigation of ionic liquid-based systems has greatly increased.²³ XPS can give information on both the electronic environment of ionic liquids^24–31 and the ionic liquid/gas surface composition.^26,31–34 XPS can be used to monitor the liquid-phase organic reactions^25,27 chemical state of metal catalysts in ionic liquids^35–37 and the electronic contribution of a substituent towards the stabilisation of the cationic charge.^28,29 XPS can reveal very subtle trends in the binding energies of cation-based components²⁶ and the hydrogen bond acceptor abilities of corresponding anions.^24,31,38 Recent studies have highlighted that the XPS signals can act as reporters to tune the electronic environment of cations and anions using ionic liquid mixtures.^38,39

In this study, we extend this method to investigate if XPS may be used to probe solute–solvent interactions in catalytic systems. We highlight the formation of a phosphineimidazolylidene palladium complex, which is employed as a probe of the solvation environment in five 1-octyl-3-methylimidazolium-based ionic liquids and 1-octyl-pyridinium tetrafluoroborate ([C₈Py][BF₄]) (see Table S1†). The effect of anion basicity on the electronic environment of the palladium centres has been investigated for five phosphineimidazolylidene palladium-containing solutions, where the anions are [OAc]⁻ (acetate), Cl⁻, [BF₄]⁻ (tetrafluoroborate), [TfO]⁻ (trifluoromethansulfonate), and [Tf₂N]⁻, as a sequence of basicity from highest to lowest.^40,41

The formation of the new phosphineimidazolylidene palladium complex is confirmed using high-resolution Pd 3d XP spectra, and the binding energy of the Pd-containing probe is shown to be sensitive to the ionic liquid solvent across a range of compositions. The impact of anion composition upon the electronic environment of the new Pd-ylidene species is investigated; our data is correlated to the Kamlet–Taft hydrogen bond acceptor ability, β. Furthermore, in the case of the deliberate investigation of simple ionic liquid-based mixtures, where a common cation is probed in the presence of mixed anions, the probe appears to experience a single “average” environment. It suggests that the ions form a single anisotropic mixture as opposed to discrete yet intimately mixed pockets of differing anion/cation combinations which could initiate segregation and preferential solute clustering.

Our data suggests that ionic liquids can contribute to catalytic processes and are much more than mere spectators in chemical reactions. Interactions of this nature can be correlated to reaction performance, providing essential information for the design of more efficient catalytic systems. This hypothesis is tested experimentally by comparison of catalyst turnover of frequencies (TOFs) for a series of standard benchmark reactions, i.e., the Pd-catalysed Suzuki reaction, carried out in a range of ionic liquids that were chosen to offer a range of both measured Pd 3d binding energies and Kamlet–Taft β values.

Experimental

Materials

All chemicals were obtained from Sigma-Aldrich or Alfa Aesar and were used as received except for 1-methylimidazole, which was distilled over calcium hydride prior to use. Lithium bis[(trifluoromethane)sulfonyl]imide was obtained from 3M and used as received. All ionic liquids investigated in this work were prepared in our laboratory using established synthetic protocols, [C₈C₁Im]Cl,⁴² [C₈C₁Im][BF₄],⁴³ [C₈C₁Im][TfO],⁴⁴ [C₈C₁Im][Tf₂N],⁴⁵ [C₈C₁Im][OAc],⁴⁶ and [C₈Py][BF₄].⁴³ The structures of the individual cations and anions investigated in this study are shown in Table S1.†

All ionic liquids were dried in vacuo (p ≤ 10⁻³ mbar) before being fully characterised by ¹H NMR spectroscopy, ¹³C NMR spectroscopy, ESI-MS and Karl Fischer titration. When ion exchange was one of the synthetic steps, ion chromatographic analysis (both anion and cation) showed that residual ion concentrations (Cl⁻, Li⁺, Na⁺, Ag⁺) were all below accepted threshold concentrations, i.e., <10 ppm. In all cases, no residual signal of either halide, or metal ions were observed during XPS analysis, i.e., the concentration was below the limit of detection. Full data, including full XPS data sets with peak deconstruction models, for all of the materials studied in this work appears in the ESI.†

Preparation of Pd-containing ionic liquid solutions

All ionic liquid solutions were prepared in an inert atmosphere (Ar) using pre-pumped and de-gassed ionic liquids. Into a mixture of NaCl (12 mg, 0.21 mmol), bromobenzene (13.1 ml, 0.125 mmol) and [Pd(PPh₃)₄] (24 mg, 0.021 mmol) in selected ionic liquid (0.25 ml), a solution of Na₂CO₃ (26 mg, 0.25 mmol) in water (0.125 ml) was injected. The resulting solution was heated to 110 °C for 3 h to ensure complete dissolution of the organometallic species. All undissolved materials were removed by filtration and all volatiles removed in vacuo.

XPS data collection

All XP spectra were recorded using a Kratos Axis Ultra spectrometer employing a focused, monochromated Al Kα source (hν = 1486.6 eV), hybrid (magnetic/electrostatic) optics, hemispherical analyser and a multi-channel plate and delay line detector (DLD) with a X-ray incident angle of 30° and a collection angle, θ, of 0° (both relative to the surface normal). X-ray gun power was 100 W. All spectra were recorded using an entrance aperture of 300 × 700 μm with a pass energy of 80 eV for survey spectra and 20 eV for high-resolution spectra. The instrument sensitivity was 7.5 × 10⁵ counts s⁻¹ when measuring the Ag 3d_5/2 photoemission peak for a clean Ag sample recorded at a pass energy of 20 eV and 450 W emission power. Ag 3d_5/2 full width half maximum (FWHM) was 0.55 eV for the same instrument settings. Binding energy calibration was made using Au 4f_7/2 (83.96 eV), Ag 3d_5/2 (368.21 eV) and Cu 2p_3/2 (932.62 eV). The absolute error in the acquisition of binding energies is ±0.1 eV, as quoted by the instruments manufacturer (Kratos); consequently, any binding energies within 0.2 eV can be considered the same, within the experimental error. Charge neutralisation methods were not required (or employed) in the measurement of these data. Sample stubs were earthed via the instrument stage using a standard BNC connector.

Samples were prepared by placing a small drop (≈20 mg) of the ionic liquid into a depression on a stainless steel sample stub (designed for powders) or on a standard stainless steel multi-sample bar (both Kratos designs). The ionic liquid samples were presented as thin films (approx. thickness 0.5–1 mm), thereby avoiding experimental complications associated with variable sample height. Initial pumping to high vacuum pressure was carried out in a preparation chamber immediately after thin film preparation to avoid significant absorption of volatile impurities. Pumping of ionic liquids was carried out with care as the high viscosities associated with these samples meant that significant bubbling due to removal of volatile impurities was observed. The pumping down process was consequently carried out slowly to avoid contamination of the UHV chamber by bumping/splashing of the ionic liquid samples. The preparation chamber pressure achieved was ≈10⁻⁷ mbar. Pumping-times varied (1–3 h total) depending upon the volume, volatile impurity content and viscosity of the sample, i.e., viscous ionic liquids were found to require longer pumping times. The samples were then transferred to the main analytical vacuum chamber. The pressure in the main chamber remained ≤1 × 10⁻⁸ mbar during all XPS measurements, suggesting that all volatile impurities, such as water, are removed, leading to high purity samples.⁴⁷

Information depth of XPS

The information depth (ID) of XPS experiments may be defined as the depth, within the sample, from which 95% of the measured signal will originate. ID is assumed to vary mainly with cos θ, where θ is the electron emission angle relative to the surface normal. If we assume that the inelastic mean free path (λ) of photoelectrons in organic compounds is of the order of ∼3 nm, at the kinetic energies employed here we can estimate ID in this geometry, when θ = 0°, ID = 7–9 nm. Consequently these data may be considered as representative of the bulk composition and do not reflect any local enhancements of concentration at the near surface region.

XPS data analysis

For data interpretation, a two-point linear background subtraction was used. Relative Sensitivity Factors (RSF), also known as the atomic sensitivity factors (ASF), were taken from the Kratos Library and were used to determine atomic percentages.⁴⁸ Peaks were fitted using GL(30) lineshapes; a combination of a Gaussian (70%) and Lorentzian (30%).⁴⁹ This lineshape has been used consistently in the fitting of XP spectra, and has been found to match experimental lineshapes in ionic liquid systems. The FWHM of each component was initially constrained to 0.8 ≤ FWHM ≤ 1.5 eV. XP spectra for [C₈C₁Im][A] ionic liquid solutions were charge corrected by setting the measured binding energy of the alkyl C 1s photoemission component (C_alkyl 1s) to 285.0 eV. This procedure has been shown to be robust for all samples when alkyl substituents on charge carriers are large (i.e., when n ≥ 8).³¹ Consequently, in this study, [C₈C₁Im]⁺-based ionic liquids were chosen for the ease of charge correction of XP spectra. The presence of additional carbon in [OAc]⁻ must be added to the existing fit model; a fitting model has been developed for charge referencing samples where the anion is [OAc]⁻.²⁴

Results and discussions

The [Pd(PPh₃)₄] catalysed Suzuki cross coupling reaction is accelerated dramatically when ionic liquids are employed as solvents.⁵⁰ The reason for this observation has been investigated and it has been concluded that the interaction between the palladium catalyst and the ionic liquid, which consequently causes the formation of a new palladium species in the solution, increases the reaction rate. The in situ formation of the phosphineimidazolylidene palladium complex results in a more thermally stable, catalytically active species in ionic liquids. In literature, the phosphineimidazolylidene palladium complex has been observed in the case of the [BF₄]⁻-based system by ESI-MS and NMR spectroscopy, with the successful determination of a crystal structure highlighted in Fig. 1.⁵¹ It must be noted that, the formation of the 1-octyl-3-methylphosphineimidazolylidene palladium complexes in all cases investigated in this paper has been confirmed by ESI-MS and XPS. In [C₈C₁Im][PF₆] (hexafluorophosphate), there is no phosphineimidazolylidene palladium complex formed.

Fig. 1 Structure of the phosphineimidazolylidene palladium complex formed in situ during the Pd catalysed Suzuki cross coupling reaction conducted in imidazolium-based ionic liquids.⁵¹

Fig. S1a† shows a survey XP spectrum for the newly formed phosphineimidazolylidene palladium complex in [C₈C₁Im][BF₄]. This ionic liquid solution will be used as a case study to describe the principal XPS features. XPS signals were observed for all expected elements, as was the case for each of the ionic liquid solutions presented herein. Previous XPS studies of ionic liquids from various groups have shown the presence of impurities in the near-surface region of ionic liquids that could not be detected using NMR or other bulk sensitive techniques.^52–56 Fig. S1a† shows no indication of any impurities present in the solution.

The regions due to elements in the ionic liquid are shown in Fig. S1b–e;† the Pd 3d region is shown in Fig. S1f.† All components fitted are labelled in Fig. S1b–e,† and have previously been identified.³¹ The XP spectra given in Fig. S1b–e† are qualitatively the same as those recorded for pure [C₈C₁Im][BF₄]. The binding energies for the peaks due to pure [C₈C₁Im][BF₄] and phosphineimidazolylidene palladium-containing solution are identical, within the experimental error (Table S2 in ESI†). This observation demonstrates that the Pd solute does not affect the electronic environment of the bulk ionic liquid sufficiently to influence the XPS binding energies, as expected as the Pd solute is in low concentrations (for detection of XPS binding energy shifts) in all cases.

FWHM of Pd 3d spectra

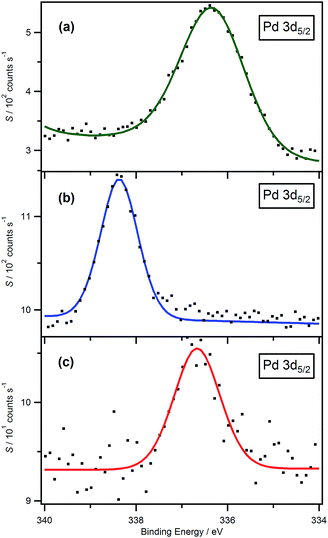
Fig. 2a and b show a comparison between the Pd 3d XP spectra for solid [Pd(PPh₃)₄] and a typical solution sample of Pd-containing ylidene complex in [C₈C₁Im][BF₄]. Upon first inspection, it is clear that the XP spectrum of the solution sample is much sharper than that of the solid [Pd(PPh₃)₄]. Indeed, the FWHM for the Pd 3d_5/2 component of the spectra are 1.0 eV and 1.8 eV, respectively. This observation may be explained as a result of charging at the surface of the non-conducting solid sample,^53,54 or, more probably, as a consequence of the photo-physics involved during the photoelectron emission. It is well known that FWHM is proportional to the lifetime of the vacancy that is left as a result of photoelectron emission (FWHM ∼ h/τ, where τ is the vacancy lifetime and h is Planck's constant). The vacancy lifetime is determined by Auger processes. In the case of Pd photoelectron emission, this process mainly involves the 5s orbital, to form an M_4,5VV Auger process. The valence electron configuration of molecular Pd, in solution, is 4d¹⁰5s⁰. However in the case of solid samples, as we move from discrete mono-metallic molecular species through to the formation of small clusters and eventually on to the bulk metal, s–d hybridisation can occur which causes a change in the electronic configuration from 4d¹⁰5s⁰ to 4d^10−ε5s^ε, where ε is less than 1. The increase in 5s orbital electron density gives rise to a shorter Pd 3d vacancy lifetime and, consequently, larger FWHM.⁵⁷

Fig. 2 Pd 3d spectra of (a) solid [Pd(PPh₃)₄], (b) the phosphineimidazolylidene palladium complex in [C₈C₁Im][BF₄] and (c) [Pd(PPh₃)₄] dissolved in [C₈Py][BF₄]. The XP spectrum obtained for solid [Pd(PPh₃)₄] was charge corrected to C_benzene 1s at 284.7 eV. The other XP spectra were charge corrected by referencing C_alkyl 1s component to 285.0 eV.

Formation of a phosphineimidazolylidene palladium complex

The Pd 3d high resolution spectrum is composed of a doublet peak which originates from the 3d orbital with a spin-orbital coupling energy difference of 5.26 eV,⁵⁸ and area ratio of 3d_5/2 : 3d_3/2 is 3 : 2 (see Fig. S1f†), as expected from theory. In this paper, unless otherwise stated, the 3d_5/2 component is selected to ensure valid comparisons, simply because the intensity for this component is greater. The Pd 3d_5/2 component in the solid sample shows a binding energy at 336.4 eV (obtained after charge correcting to the benzene carbon signal, C_benzene 1s = 284.7 eV ⁵⁹) which indicates that the Pd is in the (0) oxidation state (see Fig. 2a). The measured binding energy is consistent with values found in the literature.^49,58 By contrast, the Pd 3d_5/2 component with a binding energy at 338.4 eV measured for a solution sample in [C₈C₁Im][BF₄] indicates that the Pd is in the (+2) oxidation state and the phosphineimidazolylidene palladium complex is formed in the ionic liquid (see Fig. 2b). Moreover, the measured binding energy of Pd 3d_5/2 for the sample of [Pd(PPh₃)₄] dissolved in [C₈Py][BF₄] is found to be 336.5 eV, which is the same as that of solid [Pd(PPh₃)₄], within the experimental error (see Fig. 2c). As has been highlighted previously, the reason why imidazolium-based ionic liquids show lower electrochemical stabilities than pyridinium-based analogues is mainly due to ease of removal of the C² proton.³⁸ In pyridinium-based ionic liquids, since no palladium-containing ylidene complex is formed, the electronic environment of the Pd centre remains the same as that of the solid powder.

Qualitative effect of anion on Pd binding energy

As shown in Fig. 3, the Pd 3d_5/2 binding energies of palladium-containing solution samples follow the trend [OAc]⁻ < Cl⁻ < [BF₄]⁻ ∼ [TfO]⁻ < [Tf₂N]⁻. The lower binding energy corresponds to a more electron rich cation head group, i.e. Pd centre, which indicates that more charge has been transferred from the anion to the Pd centre for the high basicity anions, such as [OAc]⁻. These results are in good agreement with those for pure imidazolium- and pyrrolidinium-based ionic liquids.^31,38 Based upon the huge difference in catalytic performance between [Pd(PPh₃)₄] and the phosphineimidazolylidene palladium complex generated in the [BF₄]⁻-based ionic liquid, it is expected that, in the Suzuki cross coupling reaction, a more electron poor palladium centre would be more catalytically active.

Fig. 3 XP spectra of Pd 3d_5/2 for phosphineimidazolylidene palladium complexes in a range of [C₈C₁Im]⁺-based ionic liquids, (a) [Tf₂N]⁻ (b) [TfO]⁻ (c) [BF₄]⁻ (d) Cl⁻ and (e) [OAc]⁻. All XP spectra were charge corrected by referencing the C_alkyl 1s component to 285.0 eV.

Quantitative effect of anion on Pd binding energy: β vs. Pd 3d binding energy

Intermolecular interactions are one of the key factors, which determine the structure^60–64 and properties of ionic liquids, e.g. viscosity and conductivity.⁶⁵ Based upon such a correlation, the selection of a specific anion for a particular task is preceded by considering the delivery of a liquid that can provide the desired physico-chemical properties. However, in terms of quantifying the selection process, it has to revolve around the prediction of the cation–anion interactions.

Charge distribution and ion pair availability of ionic liquids are intrinsic to the formation of hydrogen-bonded networks involving both the cation of the ionic liquid and solute components. The direct quantification of these interactions in the case of a single specific ion is not straightforward. Indeed, a number of metrics have been proposed including proton affinity, dissociation energy and interaction energy, all of which are based upon semi-empirical, single molecule calculations, which omit multi-point interactions.

Kamlet–Taft parameters provide information about the interactions within a solvent and therefore describe liquid phase properties of ionic liquids. The Kamlet–Taft hydrogen bond acceptor ability, β, has been used to indicate the basicity of the corresponding anions of ionic liquids. β was found to follow the trend [Tf₂N]⁻ < [TfO]⁻ ∼ [BF₄]⁻ < Cl⁻ < [OAc]⁻ (see Table S3†).^40,41 This observation is in good agreement with the trend of measured binding energies of Pd 3d_5/2 for palladium-containing ylidene complexes in the corresponding ionic liquid-based solutions, see Fig. 4. This observation confirmed the conclusion highlighted previously,^26,31,38 that the basicity of the anions can influence the measured binding energies obtained for the solute components.

Fig. 4 Pd 3d_5/2binding energies for phosphineimidazolylidene palladium complexes in different [C₈C₁Im]⁺-based ionic liquids compared to hydrogen bond acceptor ability (β). All binding energies obtained were charge corrected by referencing the C_alkyl 1s component to 285.0 eV. It must be noted that the experimental error with the XPS measurement is of the order ±0.1 eV.

Can anion basicity impact on the reaction rate?

As mentioned previously, the Suzuki cross coupling reaction has been widely studied, using ionic liquids as reaction media.^{12,13,50,66–72} Switching from traditional organic solvents to ionic liquids can give rise to a dramatic increase in reaction rate due to the formation of a new, more reactive palladium-containing ylidene complex.^13,50 XPS of ionic liquid-based solutions offers a unique opportunity to probe this process and investigate the influence of the anion chemistry. Here we investigate the impact of anion basicity on the tuning of a catalytic system. In principle, this data could inform the systematic design of a new, more active catalyst, which will deliver high productivity in terms of reaction rate or selectivity. We report a simple palladium catalysed Suzuki crossing coupling reaction, using bromobenzene and phenylboronic acid as starting materials, processed in ionic liquids. The proton signals from both of the starting materials and the product show similar chemical shift (δ), between 7.65 and 7.15 ppm. However, the two ortho-protons within phenylboronic acid show higher δ at around 8.00 ppm, and can be easily integrated to quantify the conversion. The reaction conversion calculated by integrating the desired ¹H NMR peaks was consequently used to calculate the TOFs of the reaction.

It must be noted that the TOFs was given by assuming that no side reaction was carried out during the reaction, and thus the starting materials will only be converted to the desired product. NMR spectroscopy suggests that this assumption is valid as all observed peaks can be assigned to the starting materials, product or the solvent. Furthermore, as concluded earlier, the measured binding energies of Pd 3d_5/2 for the phosphineimidazolylidene palladium complexes in the corresponding ionic liquid-based solutions follow a trend. Consequently, three ionic liquids, with different basicity of anions, [C₈C₁Im][Tf₂N], [C₈C₁Im][BF₄] and [C₈C₁Im][OAc], were selected as the reaction solvents. This is mainly because the basicity of these three anions are significantly different, i.e. [Tf₂N]⁻ is the least basic anion whilst [OAc]⁻ is the most basic anion, with [BF₄]⁻ lying in between. The reaction rates are shown in Fig. 5.

Fig. 5 Correlation of reaction rate to Pd 3d_5/2 binding energy for a Suzuki cross coupling reaction in [C₈C₁Im]⁺-based ionic liquids. All binding energies obtained were charge corrected by referencing the C_alkyl 1s component to 285.0 eV. It must be noted that the experimental error associated with the XPS measurement is of the order ±0.1 eV. The experimental error for the calculation of TOFs is ±5%.

The measured binding energy of Pd 3d_5/2 for the [Tf₂N]⁻-based palladium-containing solution is found to be 338.7 eV, which is higher than any other binding energies obtained for the palladium centres in corresponding ionic liquid solutions. The reaction rate monitored for the Suzuki cross coupling reaction, in [C₈C₁Im][Tf₂N], is also found the largest which confirms that a more electron poor palladium centre is more catalytically active. The lower basicity the anion, the more electron poor the palladium centre, and thus the faster the reaction. The opposite is also true in the case of higher basicity anions, e.g. [C₈C₁Im][OAc]. In the case of [C₈C₁Im][BF₄], since the basicity of [BF₄]⁻ lies in between [Tf₂N]⁻ and [OAc]⁻, the monitored reaction rate in this ionic liquid was also found to be in the middle of those obtained for [Tf₂N]⁻ and [OAc]⁻, see Fig. 5. It must be noted that due to the possibility of the formation of HF in [C₈C₁Im][BF₄], the catalytic activity of the Pd centre may be influenced. In this paper, such influence on the measured TOFs was ignored. However, for future work, it is worth to investigate the method aiming to minimise the effect of the formation of HF on the catalytic reaction rate. Furthermore, since the Pd 3d binding energy of [Pd(PPh₃)₄] dissolved in [C₈Py][BF₄] is the same as that of the solid catalyst, it is expected that the TOFs of the Suzuki cross coupling reaction in [C₈Py][BF₄] should be similar with that conducted in organic solvents.

Although insufficient data has been available to quantify the effect of binding energy on the reaction rate, this is the first time that we have successfully correlated the binding energy to reaction rate, which could allow us to specifically design a metal catalytic system to accelerate catalytic reaction by selection of anions and application of ionic liquid mixtures.³⁹

Conclusions

We have successfully measured XP spectra for a range of ionic liquid solutions containing phosphineimidazolylidene palladium complexes. A comparison of binding energies obtained for solid [Pd(PPh₃)₄] and phosphineimidazolylidene palladium complex, in [C₈C₁Im][BF₄], revealed a significant difference. The palladium centre of the phosphineimidazolylidene palladium complex was found to be more electron poor. The binding energy of Pd 3d_5/2 measured for [Pd(PPh₃)₄] dissolved in [C₈Py][BF₄] was the same as that of the solid catalyst, which further confirmed that the Pd(II) centre was only formed in imidazolium-based ionic liquids.

We also show comparisons of charge corrected binding energies of Pd 3d for the phosphineimidazolylidene palladium complexes in ionic liquid solutions with varying anion. The measured binding energy of the Pd 3d_5/2 decreases as the basicity of the anion is increased, indicating that more charge was transferred from the anion to the solute for higher basicity anions such as Cl⁻ and [OAc]⁻. The Pd 3d_5/2 binding energies measured for different ionic liquid solutions could be correlated linearly to β. It has been found that the measured binding energies of Pd 3d for phosphineimidazolylidene palladium complexes in corresponding ionic liquids are proportional to the values of β for the corresponding anions.

We carried out a model Suzuki cross coupling reaction in three ionic liquids, taking into account the basicity of anions. For the first time, we have correlated the binding energy of the metal centre of a catalytic system to reaction rate. It allows us to specifically design a metal catalytic system to accelerate catalytic reactions.

Acknowledgements

We thank the EPSRC (EP/K005138/1) and Nature Science Foundation of Liaoning Province (2013020094) for financial support. PL acknowledges the EPSRC for the award of an ARF (EP/D073014/1). KRJL acknowledges Imperial College London for the award of a JRF. The authors are grateful to Dr Emily F. Smith for helpful discussions and critical advice.

Notes and references

1. J. P. Hallett and T. Welton, Chem. Rev., 2011, 111, 3508.
2. H. Olivier-Bourbigou and L. Magna, J. Mol. Catal. A: Chem., 2002, 182, 419.
3. A. Bosmann, G. Francio, E. Janssen, M. Solinas, W. Leitner and P. Wasserscheid, Angew. Chem., Int. Ed., 2001, 40, 2697.
4. V. I. Pârvulescu and C. Hardacre, Chem. Rev., 2007, 107, 2615.
5. F. Castiglione, E. Ragg, A. Mele, G. B. Appetecchi, M. Montanino and S. Passerini, J. Phys. Chem. Lett., 2011, 2, 153.
6. C. P. Mehnert, Chem.–Eur. J., 2004, 11, 50.
7. A. Riisager, R. Fehrmann, M. Haumann and P. Wasserscheid, Top. Catal., 2006, 40, 91.
8. A. Riisager, R. Fehrmann, M. Haumann and P. Wasserscheid, Eur. J. Inorg. Chem., 2006, 695.
9. T. Cremer, M. Killian, J. M. Gottfried, N. Paape, P. Wasserscheid, F. Maier and H.-P. Steinrück, ChemPhysChem, 2008, 9, 2185.
10. S. Tang, A. Babai and A. V. Mudring, Angew. Chem., Int. Ed., 2008, 47, 7631.
11. D. B. Williams, M. E. Stoll, B. L. Scott, D. A. Costa and W. J. Oldham, Chem. Commun., 2005, 1438.
12. L. J. Xu, W. P. Chen and J. L. Xiao, Organometallics, 2000, 19, 1123.
13. C. J. Mathews, P. J. Smith and T. Welton, Chem. Commun., 2000, 1249.
14. R. J. C. Brown, P. J. Dyson, D. J. Ellis and T. Welton, Chem. Commun., 2001, 1862.
15. C. M. Zhong, T. Sasaki, M. Tada and Y. Iwasawa, J. Catal., 2006, 242, 357.
16. S. M. Silva, R. P. J. Bronger, Z. Freixa, J. Dupont and P. van Leeuwen, New J. Chem., 2003, 27, 1294.
17. C. F. Weber and R. van Eldik, Eur. J. Inorg. Chem., 2005, 4755.
18. A. V. Kucherov, A. V. Vasnev, A. A. Greish and L. M. Kustov, J. Mol. Catal. A: Chem., 2005, 237, 165.
19. R. Moberg, F. Bökman, O. Bohman and H. O. G. Siegbahn, J. Am. Chem. Soc., 1991, 113, 3663.
20. F. Bökman, O. Bohman and H. O. G. Siegbahn, J. Phys. Chem., 1992, 96, 2278.
21. B. Winter and M. Faubel, Chem. Rev., 2006, 106, 1176.
22. R. Seidel, M. Faubel, B. Winter and J. Blumberger, J. Am. Chem. Soc., 2009, 131, 16127.
23. K. R. J. Lovelock, I. J. Villar-Garcia, F. Maier, H. P. Steinrück and P. Licence, Chem. Rev., 2010, 110, 5158.
24. B. B. Hurisso, K. R. J. Lovelock and P. Licence, Phys. Chem. Chem. Phys., 2011, 13, 17737.
25. N. Paape, W. Wei, A. Bosmann, C. Kolbeck, F. Maier, H. P. Steinruck, P. Wasserscheid and P. S. Schulz, Chem. Commun., 2008, 3867.
26. T. Cremer, C. Kolbeck, K. R. J. Lovelock, N. Paape, R. Wölfel, P. S. Schulz, P. Wasserscheid, H. Weber, J. Thar, B. Kirchner, F. Maier and H. P. Steinrück, Chem.–Eur. J., 2010, 16, 9018.
27. N. Taccardi, I. Niedermaier, F. Maier, H. P. Steinrück and P. Wasserscheid, Chem.–Eur. J., 2012, 18, 8288.
28. C. Kolbeck, I. Niedermaier, N. Taccardi, P. S. Schulz, F. Maier, P. Wasserscheid and H. P. Steinrück, Angew. Chem., Int. Ed., 2012, 51, 2610.
29. I. Niedermaier, C. Kolbeck, N. Taccardi, P. S. Schulz, J. Li, T. Drewello, P. Wasserscheid, H. P. Steinrück and F. Maier, ChemPhysChem, 2012, 13, 1725.
30. M. Reinmoller, A. Ulbrich, T. Ikari, J. Preiss, O. Höfft, F. Endres, S. Krischok and W. J. D. Beenken, Phys. Chem. Chem. Phys., 2011, 13, 19526.
31. I. J. Villar-Garcia, E. F. Smith, A. W. Taylor, F. Qiu, K. R. J. Lovelock, R. G. Jones and P. Licence, Phys. Chem. Chem. Phys., 2011, 13, 2797.
32. F. Maier, J. M. Gottfried, J. Rossa, D. Gerhard, P. S. Schulz, W. Schwieger, P. Wasserscheid and H. P. Steinruck, Angew. Chem., Int. Ed., 2006, 45, 7778.
33. C. Kolbeck, N. Paape, T. Cremer, P. S. Schulz, F. Maier, H. P. Steinrück and P. Wasserscheid, Chem.–Eur. J., 2010, 16, 12083.
34. K. R. J. Lovelock, Phys. Chem. Chem. Phys., 2012, 14, 5071.
35. F. Qiu, A. W. Taylor, S. Men, I. J. Villar-Garcia and P. Licence, Phys. Chem. Chem. Phys., 2010, 12, 1982.
36. A. W. Taylor, F. Qiu, I. J. Villar-Garcia and P. Licence, Chem. Commun., 2009, 5817.
37. A. W. Taylor, S. Men, C. J. Clarke and P. Licence, RSC Adv., 2013, 3, 9436.
38. S. Men, K. R. J. Lovelock and P. Licence, Phys. Chem. Chem. Phys., 2011, 13, 15244.
39. I. J. Villar-Garcia, K. R. J. Lovelock, S. Men and P. Licence, Chem. Sci., 2014, 5, 2573.
40. R. Lungwitz, V. Strehmel and S. Spange, New J. Chem., 2010, 34, 1135.
41. J. Palgunadi, S. Y. Hong, J. K. Lee, H. Lee, S. D. Lee, M. Cheong and H. S. Kim, J. Phys. Chem. B, 2011, 115, 1067.
42. J. G. Huddleston, A. E. Visser, W. M. Reichert, H. D. Willauer, G. A. Broker and R. D. Rogers, Green Chem., 2001, 3, 156.
43. P. A. Z. Suarez, J. E. L. Dullius, S. Einloft, R. F. DeSouza and J. Dupont, Polyhedron, 1996, 15, 1217.
44. H. Tokuda, K. Hayamizu, K. Ishii, M. Abu Bin Hasan Susan and M. Watanabe, J. Phys. Chem. B, 2004, 108, 16593.
45. P. Bonhôte, A. P. Dias, N. Papageorgiou, K. Kalyanasundaram and M. Grätzel, Inorg. Chem., 1996, 35, 1168.
46. Z. F. Zhang, J. G. Li, Q. G. Zhang, W. Guan and J. Z. Yang, J. Chem. Eng. Data, 2008, 53, 1196.
47. A. W. Taylor, K. R. J. Lovelock, A. Deyko, P. Licence and R. G. Jones, Phys. Chem. Chem. Phys., 2010, 12, 1772.
48. C. D. Wagner, L. E. Davis, M. V. Zeller, J. A. Taylor, R. H. Raymond and L. H. Gale, Surf. Interface Anal., 1981, 3, 211.
49. Surface Analysis by Auger and X-ray Photoelectron Spectroscopy, ed. D. Briggs and J. T. Grant, IMPublications, Manchester, 2003.
50. C. Yang, C. Tai, Y. Huang and I. Sun, Tetrahedron, 2005, 61, 4857.
51. C. J. Mathews, P. J. Smith, T. Welton, A. J. P. White and D. J. Williams, Organometallics, 2001, 20, 3848.
52. E. F. Smith, I. J. Villar Garcia, D. Briggs and P. Licence, Chem. Commun., 2005, 5633.
53. E. F. Smith, F. J. M. Rutten, I. J. Villar-Garcia, D. Briggs and P. Licence, Langmuir, 2006, 22, 9386.
54. K. R. J. Lovelock, E. F. Smith, A. Deyko, I. J. Villar-Garcia, P. Licence and R. G. Jones, Chem. Commun., 2007, 4866.
55. J. M. Gottfried, F. Maier, J. Rossa, D. Gerhard, P. S. Schulz, P. Wasserscheid and H. P. Steinruck, Z. Phys. Chem., 2006, 220, 1439.
56. H. Hashimoto, A. Ohno, K. Nakajima, M. Suzuki, H. Tsuji and K. Kimura, Surf. Sci., 2010, 604, 464.
57. X. C. Lai, M. A. Pushkin and V. I. Troyan, Surf. Interface Anal., 2004, 36, 1199.
58. J. F. Moulder, W. F. Stickle, P. E. Sobol and K. D. Bomben, Handbook of X-ray photoelectron spectroscopy: a reference book of standard spectra for identification and interpretation of XPS data, Physical Electronics, Eden Prairie, 1995.
59. The XPS of Polymers Database, ed. D. Briggs and G. Beamson, SurfaceSpectra, Manchester, 2000.
60. H. Weingärtner, Angew. Chem., Int. Ed., 2008, 47, 654.
61. S. Tsuzuki, H. Tokuda, K. Hayamizu and M. Watanabe, J. Phys. Chem. B, 2005, 109, 16474.
62. P. A. Hunt, I. R. Gould and B. Kirchner, Aust. J. Chem., 2007, 60, 9.
63. S. Tsuzuki, R. Katoh and M. Mikami, Mol. Phys., 2008, 106, 1621.
64. C. L. Hussey, J. R. Sanders and H. A. Oye, J. Electrochem. Soc., 1985, 132, 2156.
65. H. Tokuda, S. Tsuzuki, M. Susan, K. Hayamizu and M. Watanabe, J. Phys. Chem. B, 2006, 110, 19593.
66. V. Calo, A. Nacci and A. Monopoli, Eur. J. Org. Chem., 2006, 3791.
67. N. T. S. Phan, M. Van Der Sluys and C. W. Jones, Adv. Synth. Catal., 2006, 348, 609.
68. B. W. Xin, Y. H. Zhang, L. F. Liu and Y. G. Wang, Synlett, 2005, 3083.
69. Y. Sato, T. Yoshino and M. Mori, J. Organomet. Chem., 2005, 690, 5753.
70. R. Singh and S. P. Nolan, J. Organomet. Chem., 2005, 690, 5832.
71. M. L. Zhang, S. H. Zhang, G. Y. Zhang, F. Chen and J. Cheng, Tetrahedron Lett., 2011, 52, 2480.
72. G. Liu, M. Q. Hou, T. B. Wu, T. Jiang, H. L. Fan, G. Y. Yang and B. X. Han, Phys. Chem. Chem. Phys., 2011, 13, 2062.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra04662a

---