Mechanical stability of zinc oxide nanowires under tensile loading: is wurtzite stable at the nanoscale?

Abstract

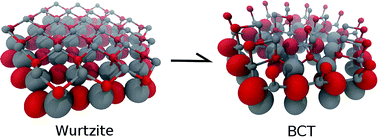
The mechanical response of zinc oxide nanowires under uniaxial tensile loading is investigated by molecular dynamics and supported by density functional calculations. Previous theoretical works predict a stress-induced phase transition which has not been observed experimentally in zinc oxide nanowires up to date. Here, we report an explanation for such a discrepancy. Our simulations reveal brittle failure at room temperature without phase transformation, in agreement with experiments. Interestingly, we also find that if the temperature is raised to 600 K, the phase transition occurs. A detailed reaction mechanism is proposed. For the first time, the associated rate constant has been calculated. Based on these results we propose an experimental procedure to finally observe the predicted phase transformation.

---

1 Introduction

Zinc oxide (ZnO) stands out as one of the most versatile nanomaterials. The technological applications of this wide-band-gap semiconductor are vast and diverse, among them we can mention: solar cell window layers, catalysis, gas and chemical sensors, optical and electrical devices, cosmetics, etc.^1–3 One of its most promising features is piezoelectricity, i.e., its potential of converting mechanical energy into electricity.⁴ The voltage induced by mechanical stress is proportional to the maximum achievable strain. Since one-dimensional (1-D) ZnO structures can withstand 5 times more strain than the bulk material, ZnO nanowires (NWs) are the ideal system to use in piezoelectric nanodevices.⁵ The synthesis, characterization and applications of 1-D ZnO nanostructures are given in ref. 2; we will avoid repetition here.

In order to benefit the development of such ZnO devices, a deeper understanding of its mechanical properties in the nanoscale is essential.^4,6 Due to the great advances in computational power, Molecular Dynamics (MD) simulations and Density Functional Theory (DFT) calculations appear as excellent tools to fulfill this purpose.

First, the results obtained from previous MD simulations are briefly summarized. Wang et al. were the first to predict that at around a strain of 10% at 300 K, ZnO NWs of up to 5 nm in diameter experience a phase transition from wurtzite (WZ, the most stable ZnO bulk structure) to a body-centered-tetragonal (BCT) structure.⁷ Later works found that the features of this transition are size dependent, particularly for the maximal stress before transformation to BCT.^8–10 Similar results were obtained for NWs with three different cross-sectional shapes,¹¹ and nanobelts.^9,12 MD simulations on larger NWs (up to 10 nm) suggested that surface defects can significantly lower the strain of transition from 6.7% (pristine NW) to 5.5%.⁵ A difference in the fracture strain (6.7% vs. 10% (ref. 7)) can be ascribed to the different approaches for long-range interactions. The simulations agree that brittle failure occurs after phase transition, at a strain of around 17%.

The BCT phase was later confirmed experimentally on ZnO(101̄0) surface reconstructions.¹³ However, it has not been observed so far on ZnO NWs. In contrast to the simulations, experiments revealed brittle fracture at much lower strains (as high as 6.2%) without any signs of phase transition.⁵ It is very important to notice, however, that all of the simulation studies described above were performed with the Buckingham potential.^14,15 This is a non-reactive pairwise potential, and therefore the quantitative aspects regarding bond breaking and bond formations should be taken with care. Especially for phase transformations, where such bond processes are crucial, the Buckingham potential can only qualitatively describe the phenomenon.

DFT calculations, on the other hand, found that the WZ–BCT transition occurs prior to fracture at 20% strain,¹⁶ at least twice the value predicted by the Buckingham potential. Still, DFT studies were performed as molecular mechanics simulations at 0 K so that the effect of atomic motion and temperature were not considered.^3,16,17 Also, the dimensions of the systems studied were very small due to the computational cost. These drawbacks prevented DFT studies from describing the brittle fractures and/or phase transitions realistically.

In summary, the Buckingham potential fails to describe the quantitative aspects of the WZ–BCT transition, and DFT cannot give insights into the effect of temperature on the mechanical properties of ZnO NWs.

Here, we report a systematic study of the mechanical response of ZnO NWs under tensile loading using a state-of-the-art reactive potential. This reactive force field (ReaxFF) accounts for bond breaking and bond formation processes. In order to test its performance, DFT calculations on 1-D nanostructures were also carried out. An excellent agreement between ReaxFF and DFT was found. Our MD simulations reveal that under tensile loading at 300 K, ZnO NWs do not experience a phase transition but instead a brittle failure, in perfect agreement with experiments. Interestingly, the transition does occur if the temperature is raised to 600 K. Through this article, we have proposed a detailed mechanism of the WZ–BCT transition in NWs, and estimate its rate constant as a function of temperature and strain. To the best of our knowledge, this has not been addressed before. Finally, we have proposed an experimental procedure to observe such a fascinating phenomenon.

2 Computational details

Ab initio calculations were performed using the Quantum Espresso/PWSCF code.¹⁸ Vanderbilt ultrasoft pseudopotentials¹⁹ were used with the Perdew–Burke–Ernzerhof²⁰ (PBE) approximation and local density approximation²¹ (LDA). A 490 eV (36 Ry) kinetic energy cutoff and a 4082 eV (300 Ry) charge density cutoff was used. The reciprocal space was sampled with an (8 × 8 × 5) and a (1 × 1 × 6) k-point grid for NWs and nanotubes (NTs), respectively. Both grids were generated automatically using the Monkhorst–Pack method.²² All of these inputs were carefully parameterized. A Gaussian broadening of 0.136 eV (0.01 Ry) was applied. The convergence of the forces for the DFT relaxations were equal to 0.02 eV Å⁻¹. The unit cells consisted of NWs and NTs of two bilayers separated by 8.4 Å from their lateral periodic images. Videos showing a NW and a NT are provided in the ESI, and explained in Fig. S1.†

Energy minimizations and molecular dynamics simulations (MD) were carried out using the Large-scale Atomic-Molecular Massively Parallel Simulator²³ (LAMMPS). The zinc–oxygen interactions were described with the reactive force field ReaxFF,^24,25 as it is implemented in the LAMMPS subroutine.²⁶ The simulations were performed with a constant number of atoms and at a constant temperature using the Nose–Hoover thermostat, with a time step of 1 fs. Unless otherwise mentioned, all NWs in this work are [0001] oriented wurtzite structures with a hexagonal cross-section exposing the {101̄0} facet. For MD simulations, seven ZnO bilayers were used to account for the possible surface reconstructions. The periodic boundary conditions were implemented for the three dimensions, keeping NWs separated by at least 20 Å with respect to their periodic images. The initial velocities were randomly assigned following a Maxwell–Boltzmann distribution. The length of the simulation box along the wire axis was increased at 0.2 m s⁻¹, simulating tensile loading. Slower stretchings did not affect the results. Tensile stress was obtained as the sum of the z component of the stress tensor of each atom, as calculated by the compute_stress_atom subroutine included in LAMMPS.

Nudged elastic band (NEB) calculations were performed following the discussion in ref. 27–29 as implemented in LAMMPS, using 32 images between metastable states. The associated activation energy was converged with three supercells (see Fig. S9†).

3 Results and discussion

3.1 ReaxFF performance on nanostructures

Originally, a ReaxFF for zinc and oxygen was parametrized for bulk and surface structures using the B3LYP-functional^24,25 and a good agreement with DFT calculations was observed. Here, we extended the testing to nanostructures such as NWs and NTs, using the most commonly implemented DFT functionals: GGA and LDA. Since some differences could arise from the different quantum mechanical approaches, bulk and surface properties were calculated as well. Table 1 shows the ZnO bulk parameters and energies according to experimental results, GGA, LDA, and ReaxFF. Our DFT results are in good agreement with the measured values and coincide with previous theoretical works.^1,32–36 As usual, LDA overestimates the cohesive energy, however, it correctly estimates the energetic difference between structures. The accordance between the force field and our ab initio calculations is as good as in the original works.

Table 1 Measured and calculated lattice constants (a,b,c), cohesive energy of the ZnO wurtzite per zinc–oxygen pair (E_WZ), cohesive energy difference per pair between rocksite and wurtzite (ΔE_RS–WZ), and between the zinc-blende and wurtzite structures (ΔE_ZB–WZ)

	Experiment	GGA	LDA	ReaxFF
a and b (Å)	3.250 (ref. 30)	3.287	3.185	3.282
c (Å)	5.207 (ref. 30)	5.303	5.152	5.305
EWZ (eV)	7.56 (ref. 31)	7.28	8.98	7.76
ΔERS–WZ (eV)	—	0.292	0.221	0.402
ΔEZB–WZ (eV)	—	0.014	0.013	0.021

---

Next, the force field performance on 1-D structures was evaluated. Several ZnO NWs and NTs of different diameters were relaxed using both DFT and ReaxFF. An example of each structure is depicted in Fig. 1a (a complete set of geometries is provided in Fig. S3†). Their stability was quantified via the formation energy, according to

E_f = E_1D(m)/m − E_bulk (1)

where E_1D(m) is the energy of a NW or NT with m ZnO pairs, and E_bulk is the energy of the wurtzite bulk per pair. As can be observed in Fig. 1b, the DFT and ReaxFF curves show the same trends. Our DFT results using GGA are in perfect agreement with the work of Shen et al.³³ who predicted that ZnO NTs are more stable than ZnO NWs below a crossover point near 38 atoms. According to the LDA results, the crossover occurs at around 26 atoms, which is very close to the force field prediction (at around 23 atoms).

Fig. 1 (a) Unit cell cross sections for a NW and a NT with 48 and 32 atoms, respectively. (b) Formation energy E_f of several NWs and NTs after relaxation according to GGA, LDA, and ReaxFF. Points have been connected with lines in order to ease the comparison.

These results provide solid evidence that ReaxFF is a very reliable and suitable tool to study ZnO 1-D nanostructures. Its reproducibility and agreement with DFT calculations is remarkable, allowing us to confidently explore the mechanical properties of ZnO NWs.

3.2 Mechanical stability

In this section, the response of the ZnO NWs against axial loading is studied. MD simulations were carried out on five [0001] oriented hexagonal NWs of different diameters (detailed in Table 2) at three different temperatures: 100, 300, and 600 K. In order to choose the surface facet, we focused on the two most commonly observed in X-ray diffraction³⁷ and high-resolution scanning tunneling microscopy:³⁸ [101̄0] and [112̄0]. After a careful study of the surface stability (shown in Fig. S4 and S5 and discussed in the text in the ESI†) the [101̄0] facet was chosen for further calculations for being the most stable.

Table 2 Diameter (d) and number of atoms (n) per unit cell for the NWs selected to perform molecular dynamics. Top views are also shown

	NWI	NWII	NWIII	NWIV	NWV
d [Å]	9.6	16.8	23.2	29.4	36.2
n	336	756	1344	2100	3024
Top view

---

Fig. 2 shows tensile stress as a function of axial strain. As NWs are stretched, the bond distance increases, and so does the force that attempts to counteract the process. This causes the stress to increase almost linearly with the strain, a typical feature of an elastic deformation. This implies that a complete recoverability from strain is possible if the stress is removed. Below 600 K, the stress eventually becomes so high that the structure can no longer hold, leading to brittle fracture and the formation of an amorphous neck. Within the neck, the load is relieved by local relaxations, while far from the neck, the atoms return to their crystalline equilibrium positions. Consequently, the tensile stress falls abruptly to lower values (see breaks at 100 and 300 K in Fig. 2). These are typical features of plastic deformations. In agreement with previous work, simulations at 100 and 300 K show that the response of uniaxial loading is size dependent.^8–10 However, the differences are relatively small. The strain of the brittle fracture is actually more sensitive to the temperature, decreasing from 20% at 100 K, to 13% at 300 K.

Fig. 2 Tensile stress as a function of strain for the chosen nanowires at 100, 300, and 600 K.

In contrast to all previous MD studies, our simulations show that the WZ–BCT transition does not occur at 300 K, instead brittle failure is observed. This is in perfect agreement with the experimental finding.⁵ Interestingly, the transformation does occur at 600 K, as is evident from Fig. 2 (bottom panel). A clear size-dependent behavior is found for the strain of the phase transition with the transition occurring at a higher strain for wider NWs. The resulting BCT structure is sufficiently stable to endure further stretching, up to a 20% strain. These results indicate that the temperature plays a key role in the process. Details regarding the phase transition are given in Section 3.4.

In order to quantify the stiffness of these materials the Young’s modulus (Y) was calculated, shown in Table 3. A NW with a large value of Y is relatively unstretchable, i.e., a large stress is required for a given strain. The values of Y are in the order of 170 GPa, which is one order of magnitude greater than in ductile materials (e.g. gold NWs, Y ≈ 60 GPa (ref. 39)), one order of magnitude lower than in rigid materials (e.g. carbon NTs, Y ≈ 1800 GPa (ref. 40)), and about the same order but higher than in the ZnO wurtzite bulk (Y ≈ 144 GPa).

Table 3 Young’s moduli Y of NWs from MD at 300 K

	NWI	NWII	NWIII	NWIV	NWV
Y [GPa] WZ	213	177	172	170	163
Y [GPa] BCT	187	142	135	131	128

---

The Young’s modulus was found to decrease with the increase of the NW diameter, in agreement with previous simulations.^8,9 This behavior has been ascribed to the high radial concentration of atoms, which in turn is due to the surface compression.⁴¹ Remarkably, surface compression is also responsible for the opposite effect, i.e., the increase of Y with the increase of the NW diameter.⁶ Due to the Poisson effect,⁴² radial compression induces longitudinal elongation of NWs, which in turn decreases the Young’s modulus. Since this so-called intrinsic strain decreases as the NWs get wider, Y increases. Briefly, Y first decreases with the diameter increase due to the high radial concentration of atoms, and then increases to the bulk value due to the decrease of the longitudinal elongation. This behavior has been experimentally observed in cobalt NWs wider than 70 nm.⁶ Although simulating NWs of such dimensions is beyond our computational capacity, we found convincing evidence of the intrinsic strain. The equilibrium lattice parameter “c” of ZnO was found to decrease with the increase of the NW diameter (see Fig. S6†).

Although reported experimental values change from one work to the other (from 20–58 GPa (ref. 43–50) to 100–200 GPa (ref. 41, 51–55)) all of them agree that the Young’s modulus decreases with the NW diameter,^8,9 which is in line with the theoretical outcome.

Table 3 also shows the Young’s modulus of NWs in the BCT phase. The same trend of Y with respect to the diameter is found, although in this case, values are around 20% lower than that of the WZ phase. Results for NW_I, the thinnest of the set, follow the same trends described in this section.

3.3 Structural and thermodynamic aspects

The equilibrium structures at zero strain for NW_II in WZ and BCT phases are provided in Fig. 3. The most noticeable aspect of the BCT structure is the presence of concentrically aligned squares (formed by four neighboring atoms), i.e., all the square planes intersect at the NW central axis. This is significantly different from the BCT bulk structure, where the square planes are all parallel to each other.⁷ Just like in the wurtzite case, in the BCT structure, every atom has four first neighbors. However, one of the tetrahedral angles is more acute (around 91°), which is one of the square vertices. These structural differences manifest in the vibrational density of states (VDOS), where WZ and BCT phases can be easily distinguished (see details and Fig. S7 in the ESI†).

Fig. 3 Top view of the wurtzite and body-centered-tetragonal structures of NW_II. The side view is restricted to the atoms inside the blue dashed rectangle shown in the top view.

Valuable information can be obtained from the equilibrium energy of WZ and BCT NWs as a function of strain. With this purpose, NWs in both structures were fully relaxed at several fixed lengths (along the c-axis) using ReaxFF and DFT. To facilitate the comparison, the energies and strains are referred to that of the corresponding WZ NW at equilibrium and zero strain. As deduced from Fig. 4a, ab initio calculations verify that BCT NWs are stable structures. In fact, they show that for NW_I the BCT phase is even more stable than the WZ phase (if their equilibrium energies are compared). This is also the case for NW_II, according to the GGA results. A similar analysis was made for both phases in the bulk material,⁷ in which it was found that the BCT phase becomes the most stable phase at stresses higher than 7 GPa.

Fig. 4 (a) Energy per ZnO pair in WZ and BCT nanowires as a function of the strain according to the force field (RFF) and DFT (LDA and GGA). For each method, the energy and strain are referring to that of the corresponding wurtzite NW in equilibrium. The strain at which the RFF curves intersect is the crossover strain. The only points shown are the WZ_LDA and WZ_GGA values to avoid confusion. (b) Strain of the crossover as a function of the NW diameter, according to ReaxFF. The inset shows the dependence on the number of atoms per unit cell.

A crucial feature to study is the crossover point, i.e., the point at which the curves of both structures intersect in Fig. 4a. The strain at the crossover point indicates the strain at which the BCT phase becomes more stable than the wurtzite phase. As the diameter increases (from NW_I to NW_II), the crossover shifts to greater strains and higher energies. ReaxFF slightly underestimates the relative stability of the BCT NWs. Indeed, the relative energy difference between ReaxFF and LDA is of the same order as that between the two DFT techniques studied. Moreover, the tendency of the crossover to shift to higher strains and energies with the NW diameter is correctly captured by the force field. This allows us to explore the larger systems using ReaxFF.

It is instructive to study how fast the crossover shifts with the NW size. If at a certain diameter the crossover occurs at a large strain value (25%, for instance) it is very unlikely that the phase transition will take place since at that strain the wire suffers brittle failure even at very low temperatures. With this motivation, the crossover point was calculated using ReaxFF for several NWs with diameters from 9 Å to almost 50 Å. As shown in Fig. 4b, the crossover strain as a function of the diameter converges asymptotically to a strain of ∼8%, which is safely below the strain of brittle failure (Fig. 2). This implies that the WZ–BCT transition could also occur in NWs wider than 5 nm under tensile loading. Furthermore, the converged value of crossover strain may be even lower considering that the force field underestimates the stability of BCT NWs.

3.4 Phase transition mechanism

Results so far indicate that at certain strains, the BCT structure is thermodynamically favored over the WZ structure. However, this is not sufficient to claim that the former should exist in nature: a kinetic insight is required. Indeed, simulations suggest that the process is kinetically hindered (Fig. 2). In order to finally predict its feasibility, the mechanism of the WZ–BCT transformation was investigated. Previous simulations have already found that the stress-induced WZ–BCT phase transition originates from the surface and spreads radially toward the NW core.⁵ We have found the same trend for NWs of different diameters and at different temperatures. We also found that the process occurs through metastable steps, involving the bond breaking and bond formation between atoms along strings aligned to the c-axis. Later, neighboring strings undergo the same process. In the following discussion, such strings will be referred to as columns, as highlighted in Fig. 5b (C1–C3). NW_II at 11% strain is chosen as an illustrative example. Three reaction pathways were proposed, depicted in Fig. 5c. For clarity, only C1–C3 columns are shown instead of the whole NW.

Fig. 5 (a) Reaction coordinates for three pathways of the wurtzite–BCT transformation for NW_II at 11% strain. Only the first steps of the mechanism are shown (the full reaction cascade is shown in the ESI†). The pathway with the lowest activation energy is colored blue. The inset shows the activation energy associated with the blue pathway as a function of the strain for NW_II, NW_III, and NW_IV. (b) Top and side views of NW_II in the wurtzite structure. Atoms that experience bond breaking or bond formation are depicted as red (oxygen) and gray (zinc) spheres. Three atom columns are highlighted as C1–C3. (c) Relocation of the atoms along the reaction pathways. For the sake of clarity, only the highlighted atoms in (b) are shown. Three-coordinated atoms are remarked by a yellow ellipse.

The first reaction pathway was inspired by MD simulations, in which it was observed that the bond reorganization takes place first in two vicinal columns, and only then continues in a third one (s1–s2–s3a–s4a–s5 in Fig. 5c). In the second path, the bond breaking/formation is completed in one column, before continuing in the second one (s1–s2–s3b–s4a in Fig. 5c). Finally, in the third path, the phase transition starts in one column and spreads in neighboring columns before completing the process in the first one (s1–s2–s3a–s4c in Fig. 5c).

The associated activation energies are shown in Fig. 5a. In general, the instability of the stages increases with the number of unsaturated atoms (highlighted in yellow in Fig. 5c). This immediately discards the third pathway. The first two paths are close in energy, but the second implies greater angle distortions, making it energetically unstable with respect to the first one. In conclusion, the first pathway is the one with the lowest activation energy.

At the end of this path, columns C1 and C2 have acquired the BCT structure. In order for the phase transition to be completed, this process has to be repeated several times. In each cycle, a new column pair transforms from WZ to BCT, from the surface to the NW core, as explained above.

NEB calculations associated with the entire process show that the phase transition occurs in a cascade fashion: from stage 4a on, the reaction proceeds energetically downhill (see Fig. S8†). Therefore, the transformation of columns C1 and C2 is the rate-determining step of the WZ–BCT conversion. The same behavior was observed at different strains and NW diameters.

Since the energy required for bond breaking declines as the bonds get longer, the uniaxial tensile loading should decrease the activation energy. This is confirmed in the inset of Fig. 5a, where the activation energy for the phase transition (E_a) as a function of the strain is shown for three NWs. The three curves follow very similar trends, with slightly higher values for wider NWs. This is in agreement with the increase of the phase transition strain with the increase of the NW diameter (Fig. 2, bottom panel).

Using the Arrhenius formula it is possible to estimate the rate constant of the WZ–BCT transformation:

where A is the pre-exponential factor, E_a is the activation energy, k is the Boltzmann constant, and T is the temperature. Fig. 6 shows the rate constant dependence on temperature and strain for NW_II, assuming a pre-exponential factor A = 10¹³ s⁻¹. For the sake of clarity, these results are shown in two plots, at low and high temperatures. The strain is restricted to values higher than or equal to that of the WZ–BCT crossover (Fig. 4b); below these values the phase transition becomes infeasible. The rate constant values for high temperatures are in perfect agreement with our MD simulations. They both predict that at 10% strain and 600 K the phase transition should occur in a few picoseconds. Fig. 6 also reveals that the WZ–BCT transformation can occur at lower temperatures but at prohibited times for MD simulations (due to the computational cost).

Fig. 6 Logarithm of the rate constant for the WZ–BCT transition (log₁₀[k_t]) as a function of the temperature and the strain. Diagram regions in which brittle fracture was observed instead of phase transition (according to MDs) are highlighted in green. Values of some contour lines are labeled to ease the analysis. (a) Low temperatures. (b) High temperatures.

As observed in Fig. 2, brittle failure can occur instead of phase transition. These cases are highlighted as green regions in the rate diagrams of Fig. 6. Outside them, thermal motion of atoms is sufficient to reach the activation energy so that phase transition occurs before brittle fracture.

On the basis of the results exposed in this work, we suggest that experiments should attempt to reach high strains (like 6% as in ref. 5) but also high temperatures in order to observe the WZ–BCT transition. According to Fig. 2, at a strain of 6% increasing from room temperature to 600 K increases the rate constant of the transition by almost four orders of magnitude.

The rate constant dependence on the temperature is of paramount importance for the practical scope of solar cells. For instance, the solar panels of spacecrafts in the inner solar system must support temperatures from 116 K in the shade to 424 K on the sun-facing side.⁵⁶ Results obtained here can be used as a guideline to promote or prevent the structural transformation on such ZnO based devices. For the first case, Fig. 6 shows the strains and temperatures that are optimal for a fast and safe transition (far from brittle failure). The simplest strategy to avoid the transformation is to keep the tensile loading below 5% strain, or higher, depending on the nanowire diameter (Fig. 4b).

4 Conclusions

The response of zinc oxide nanowires under tensile loading was investigated by ab initio and reactive force field calculations. In agreement with the experimental observation, our simulations show that wurtzite nanowires at 300 K do not undergo a phase transition to the body-centered-tetragonal structure, but instead undergo brittle failure. Previous MD studies based on the Buckingham potential failed in this prediction. However, we found that the transformation does occur if the loading takes place at 600 K. The trends observed in nanowires of up to 5 nm in diameter suggest that this transition can occur also in wider nanowires. The reaction mechanism involves bond rearrangement in two neighboring strings along the c-axis, which later spreads from the surface to the NW core. The associated rate constant was found to be strongly dependent on the temperature and the strain on the nanowire. We believe that this may be used as a guidance for future experimental investigations.

Acknowledgements

This work was supported by CONICET PIP 11220110100992, Universidad Nacional de Córdoba, and ANPCyT Program BID (PICT 2010-1233). The authors thank the Texas Advanced Computer Center (TACC) for access to the Stampede supercomputer. Thanks also to the High Performance Computational Center (UNC, Córdoba, Argentina) for access to the Cristina supercomputer. F.M.Z. thanks CIN for the fellowship granted.

References

1. H. Morkoç and U. Özgür, in General Properties of ZnO, Wiley-VCH Verlag GmbH and Co. KGaA, 2009, pp. 1–76.
2. Y. Zhang, M. K. Ram, E. K. Stefanakos and D. Y. Goswami, J. Nanomater., 2012, 2012, 624520.
3. S. Xu and Z. Wang, Nano Res., 2011, 4, 1013–1098.
4. Z. L. Wang and J. Song, Science, 2006, 312, 242–246.
5. R. Agrawal, B. Peng and H. D. Espinosa, Nano Lett., 2009, 9, 4177–4183.
6. X. Huang, G. Li, L. B. Kong, Y. Z. Huang and T. Wu, Nanoscale, 2013, 5, 11643–11648.
7. J. Wang, A. Kulkarni, K. Sarasamak, S. Limpijumnong, F. Ke and M. Zhou, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 172103.
8. J. Wang, P. Xiao, M. Zhou, Z. R. Wang and F. J. Ke, J. Appl. Phys., 2010, 107, 023512–023517.
9. K. Momeni and H. Attariani, Phys. Chem. Chem. Phys., 2014, 16, 4522–4527.
10. J. He, S. Nagao, J. Wu and Z. Zhang, Proceedings of the 24th Nordic Seminar on Computational Mechanics, 2011, pp. 244–247.
11. W. Lee, J. Chang, S. Ju, M. Weng and C. Lee, Nanoscale Res. Lett., 2011, 6, 352.
12. Z.-H. Hong, T.-H. Fang and S.-F. Hwang, Comput. Mater. Sci., 2011, 50, 1944–1950.
13. M.-R. He, R. Yu and J. Zhu, Angew. Chem., Int. Ed., 2012, 51, 7744–7747.
14. D. J. Binks and R. W. Grimes, J. Am. Ceram. Soc., 1993, 76, 2370–2372.
15. J. Kulkarni, M. Zhou and F. J. Ke, Nanotechnology, 2005, 16, 2749.
16. R. Agrawal, J. T. Paci and H. D. Espinosa, Nano Lett., 2010, 10, 3432–3438.
17. M. J. Spencer, Prog. Mater. Sci., 2012, 57, 437–486.
18. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
19. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895.
20. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
21. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211.
22. J. H. Monkhorst and D. J. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
23. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
24. D. Raymand, A. C. van Duin, M. Baudin and K. Hermansson, Surf. Sci., 2008, 602, 1020–1031.
25. D. Raymand, A. C. van Duin, D. Spångberg, W. A. G. III and K. Hermansson, Surf. Sci., 2010, 604, 741–752.
26. H. M. Aktulga, J. C. Fogarty, S. A. Pandit and A. Y. Grama, Parallel. Comput., 2012, 38, 245–259.
27. G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985.
28. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
29. A. Nakano, Comput. Phys. Commun., 2008, 178, 280–289.
30. E. H. Kisi and M. M. Elcombe, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1989, 45, 1867–1870.
31. U. of Rhode Island. Coastal Resources Center, CRC handbook of chemistry and physics, CRC Press, Cleveland, Ohio, 1978.
32. B. Meyer and D. Marx, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 035403.
33. X. Shen, P. B. Allen, J. T. Muckerman, J. W. Davenport and J.-C. Zheng, Nano Lett., 2007, 7, 2267–2271.
34. Z. Fu-Chun, Z. Zhi-Yong, Z. Wei-Hu, Y. Jun-Feng and Y. Jiang-Ni, Chin. Phys. B, 2009, 18, 2508.
35. K. Sarasamak, A. J. Kulkarni, M. Zhou and S. Limpijumnong, Phys. Rev. BPhys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 024104.
36. A. Zaoui and W. Sekkal, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 174106.
37. W.-J. Li, E.-W. Shi, W.-Z. Zhong and Z.-W. Yin, J. Cryst. Growth, 1999, 203, 186–196.
38. U. Diebold, L. V. Koplitz and O. Dulub, Appl. Surf. Sci., 2004, 237, 336–342.
39. C.-C. Röhlig, M. Niebelschütz, K. Brueckner, K. Tonisch, O. Ambacher and V. Cimalla, Phys. Status Solidi B, 2010, 247, 2557–2570.
40. M. M. J. Treacy, T. W. Ebbesen and J. M. Gibson, Nature, 1996, 381, 678–680.
41. R. Agrawal, B. Peng, E. E. Gdoutos and H. D. Espinosa, Nano Lett., 2008, 8, 3668–3674.
42. G. N. Greaves, A. L. Greer, R. S. Lakes and T. Rouxel, Nat. Mater., 2011, 10, 823–837.
43. X. D. Bai, P. X. Gao, Z. L. Wang and E. G. Wang, Appl. Phys. Lett., 2003, 82, 4806–4808.
44. K. Yum, Z. Wang, A. P. Suryavanshi and M.-F. Yu, J. Appl. Phys., 2004, 96, 3933–3938.
45. Y. Huang, X. Bai and Y. Zhang, J. Phys.: Condens. Matter, 2006, 18, L179.
46. H. Ni and X. Li, Nanotechnology, 2006, 17, 3591.
47. J. Song, X. Wang, E. Riedo and Z. L. Wang, Nano Lett., 2005, 5, 1954–1958.
48. M. P. Manoharan, A. V. Desai, G. Neely and M. A. Haque, J. Nanomater., 2008, 2008, 849745.
49. S. Hoffmann, F. Östlund, J. Michler, H. J. Fan, M. Zacharias, S. H. Christiansen and C. Ballif, Nanotechnology, 2007, 18, 205503.
50. A. Desai and M. Haque, Sens. Actuators, A, 2007, 134, 169–176.
51. Q. Chen, Y. Shi, Y. S. Zhang, J. Zhu and Y. J. Yan, Phys. Rev. Lett., 2006, 96, 075505–075508.
52. J. Zhou, C. S. Lao, P. Gao, W. Mai, W. L. Hughes, S. Z. Deng, N. S. Xu and Z. L. Wang, Solid State Commun., 2006, 139, 222–226.
53. B. Wen, J. E. Sader and J. J. Boland, Phys. Rev. Lett., 2008, 101, 175502.
54. L. W. Yang, X. L. Wu, T. Qiu, G. G. Siu and P. K. Chu, J. Appl. Phys., 2006, 99, 074303.
55. D. Jiang, C. Tian, Q. Liu, M. Zhao, J. Qin, J. Hou, S. Gao, Q. Liang and J. Zhao, Mater. Sci. Eng., A, 2014, 610, 1–4.
56. MultiMedia, Staying Cool on the ISS, 2001, http://science.nasa.gov/science-news/science-at-nasa/2001/ast21mar_1/.

---

Footnotes

† Electronic supplementary information (ESI) available: Videos and figures are available. See DOI: 10.1039/c5ra04518e

‡ These authors contributed equally to this work.

---