Fast mold surface temperature evolution: relevance of asymmetric surface heating for morphology of iPP molded samples

Abstract

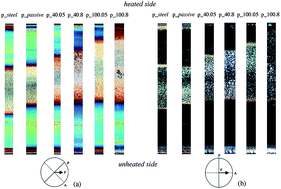
It is widely accepted that mold temperature has a strong effect on the amount of molecular orientation and morphology developed in a non-isothermal flowing melt. In this work, this effect was investigated in fast and asymmetric thermal conditions. Therefore, a well-characterized isotactic polypropylene was injected in a rectangular mold cavity conditioned by a purpose developed thin electric heater. Temperature evolution on the mold surface influences the cooling rates near the surface that, in turn, reduces flow stresses and facilitates molecular relaxation. Moreover, asymmetrical thermal conditions have a strong influence on the melt flow field by changing its distribution along the cavity thickness. As a consequence, the morphology distribution of the molded samples was asymmetric and showed complex and peculiar features. It was accurately characterized by optical microscopy and FESEM analysis and compared with the orientation distribution obtained by birefringence measurements.

---

Introduction

Injection molding is currently being utilized in a wide variety of new and unexpected applications. The current desire for smaller, cheaper, highly integrated, and more versatile products has spurred its increased use and acceptance in fields where more expensive and time-consuming techniques are currently applied. The possibility to obtain objects with particular dimensions spanning from meter to micron ranges and with good replicability of microfeatures^1,2 allows its application to a host of productions such as electronics apparatus,³ medical devices⁴ and optical systems.

It is clear that, such applications require a fast, good and repeatable control of all the processing parameters. In particular, the mold surface temperature is probably the most important one.^5–8 The negative influence of unsatisfactory and non-uniform mold temperatures distribution, indeed, cannot be balanced out by changing other process parameters. It influences not only the process productivity but also the shrinkage, warpage, and surface finishing of the molded parts. Huang et al.⁹ have found that the mold temperature has significant effect on both diameter dimensions and tooth thickness of injection-molded micro gears.

In general, high mold temperatures improve the flow behavior of the polymer in the mold, reduce the molecular orientation and improve the surface gloss of the parts. However, it also leads to slower cooling, and thus to high component costs. Flashing, polymer degradation and sink marks are additional defects related to a high mold temperature. On the contrary, low mold temperature can induce premature freezing of the melt and thus requires an increase of the filling pressure. In that case, the part generally presents weak weld lines, poor surface finishing and imperfect reproduction of micro-structured surfaces.

Especially in the case of micro injection molding, where high fidelity surface replication is requested, permanently high mold temperatures are generally adopted.^10,11 Alternatively, a continuous mold temperature evolution is attempted in order to reduce the cycle time and to keep the process economically attractive. In that case, the mold needs to be first heated above the glass transition or crystallization temperature of the polymer and, after complete mold filling, to be cooled down in order to cool the part and facilitate its extraction. The rapidity of the temperature evolution is obviously essential.

Jeng et al.¹² proposed to control mold temperature by achieving heating and cooling in the mold channel system by alternating superheated steam and cold water. Wang et al.¹³ also proposed a heating method based on the electrical rods heaters located inside the mold channels. In all these cases, the temperature cycles required several tens of seconds to take place.

For this reason, some authors proposed fast heating devices suitable to increase temperature only at mold surface and only during the filling phase. Chen et al.^14,15 proposed electromagnetic induction heating, combined with mold temperature cooling. This method allows to increase the mold surface temperature of about 50 °C in few seconds (3–4 s). Furthermore, the temperature increase resulted to be confined in a small layer (around 100 μm) at the mold surface, allowing a fast cooling phase. This approach was successfully applied for reduce the surface defects in objects produced by microcellular injection molding.¹⁶

Chang et coworkers¹⁷ and Yu and coworkers¹⁸ developed systems based on infrared heating. Yao et al.¹⁹ proposed a method based on the proximity effect between a pair of mold inserts facing each other with a small gap and forming a high-frequency electric loop. Because of the proximity effect, the high-frequency current will flow at the inner surfaces of the facing pair, thus selectively heating the mold surface.

However, all these methods require additional design and tool cost, present safety problems and do not allow an efficient cycle time. Jansen²⁰ developed a rapid thermal response (RTR) molding system based on a thin heating layer sandwiched between two insulation layers. The application of such sandwiches directly on the mold surface allows a cycled control in a large temperature range within less than 10 s.^21–23

The optimal mold temperature level is a parameter specific of the material and represents a compromise between part quality and production cost.^24–27 However, even when the optimal value of the mold temperature is found, continuous spatial and temporal variations during the production cycle may cause uncontrolled defects in the parts quality. In particular, spatial non-uniform temperature distribution can be caused by both non-correct design of the mold configuration and ineffective temperature control. Localized temperature peaks can induce warping tendency, mechanical weakness and poor surface finishing difficult to correlate with the problems source. Any direct control requires the use of temperature probes and the costly and unsafe interruption of the production cycle.

Despite the huge literature dedicated to the effect of mold temperature on the quality of the injected molded samples, only little attention was devoted to the effect of local fast and asymmetric temperature variations on the part morphology. The asymmetrical effects on the melt flow behavior are difficult to predict and can develop complex stress fields responsible for mechanically un-equilibrated molded parts.

On the other hand, the correct comprehension of these effects and their control opens the possibility to project and develop molded parts with complex 3-dimensional structures in an optimal fashion, enabling the fabrication of devices with unprecedented multifunctional performance. This process has considerable design freedom to enable creation of components with complex and controllable anisotropic thermo-mechanical behavior via the prescribed morphology type, shape, size, orientation, and even spatial variation of these parameters.

In this work, a thin multilayer heater made of poly(amide-imide) and carbon black composite film was developed and used to quickly and accurately control the mold surface temperature during the process cycle. The effects of the power and the duration of an asymmetric heating pulse on the morphology development of the isotactic polypropylene sample are investigated and correlated to the mold processing conditions.

Experimentals

Materials

The polypropylene (iPP) grade adopted in this study was supplied by Montell (now Basell), and its commercial name is T30G (non-nucleated, M_w = 376 000, M_w/M_n = 6.7, tacticity = 87.6%). An extensively characterization as far as rheology and crystallization kinetics can be found elsewhere.^{24–26,28–30}

The thin heater layered on the mold surface was made of a poly(amide-imide) (PAI) carbon back compound obtained by solvent casting. The poly(amide-imide) (PAI) was kindly supplied by Akron Polymer Systems, APS. The solvent used for the solvent casting process is Dimethylacetamide (DMAc – Sigma Aldrich, synthesis grade) with a solid concentration of about 8 wt%. The high conductive carbon black (CB particles adopted), ENSACO 260 – TIMCAL (Switzerland), have a particle size below 60 nm, an apparent density of 170 g l⁻¹, a specific surface of 70 m² g⁻¹ and a specific volume resistivity of 5.0 Ω cm. The casting process used to obtain the electrical heater is reported elsewhere.²³

Injection molding experiments

A 70-ton Negri-Bossi reciprocating screw, injection molding machine was used for the experiments. The polymer was injected into a line gated rectangular cavity having length L = 70 mm, width W = 20 mm, and thicknesses S = 1 mm. Fig. 1 shows the sample geometry adopted for the injection experiments.

Fig. 1 Sample geometry adopted for the injection experiments.

The molding machine and the mold were equipped with four piezoelectric pressure transducers located in the non-moving part of the mold: one in the injection chamber (P0), one just before the gate (P1) and two in the cavity (P2 and P3) at 15 and 60 mm downstream from the gate position, respectively. Moreover, two temperature sensors were located in the cavity, in positions P2 and P3. The carbon black thin heater film had a thickness of 50 μm, and a sheet conductivity of 40 Ω square. In order to assure thermal and electrical insulation, it was located between two insulating layers, both made of polyimide. Fig. 2 shows a sketch of all the layers located on the mold surface and their thicknesses. The heater is layered on a surface of 35 × 20 mm², corresponding to about half of the cavity length.

Fig. 2 Sketch of the heating layers located on the mold surface.

Temperature evolution data were measured with a thin thermocouple probe (type T) on the steel layer, which get in contact with the polymer while it fills the cavity. The thermocouple signal was read by a Kistler (mod. DataFlow) data acquisition system (frequency of 100 Hz) and stored in a notebook computer.

All the injection molding experiments were carried out adopting 4 cm³ s⁻¹ as volumetric flow rate (cavity filling time was about 0.5 s), a melt injection temperature of 220 °C and a mold temperature of 25 °C. The experiments selected for this paper are listed in Table 1.

Table 1 Operating conditions used for the injection molding experiments. P_packing = packing pressure; Q = volumetric flow rate; T_i = injection melt temperature; T_mold = temperature of the mold before heater activation; P = electrical power applied on an area of 700 mm²; T level = temperature reached on the steel layer; t_h = time that the heater is activated after the polymer reaches position P2. The time that the heater was activated before the contact with the filling polymer in P2, t_a, is 2 s

Ppacking (bar)	Packing time (s)	Q (cm^3 s^−1)	Tmelt (°C)	Tmold (°C)	Gate thickness (mm)	Cavity thickness (mm)	Test run	P (W)	T level (°C)	th (s)	ta (s)
							p_steel	0	25	0	0
							p_passive	0	25	0	0
300	2	4	220	30	1	1	p_40.05	40	80	0.5	2
							p_40.8	40	80	8	2
							p_100.05	100	140	0.5	2
							p_100.8	100	140	8	2

---

As reference for the other experiments, the p_steel experiment was carried out by replacing the whole heater system, reported in Fig. 2, with a single steel layer of the same thickness. As shown below all heating experiments reported in this work were carried out activating the heater 2 s before the polymer reached the position P2, where pressure and temperature were measured. After that, the electrical power was held active for an additional heating time, t_h. During the heating phase, temperature on the heated side of the cavity stabilizes to values, which obviously depend upon the heating power adopted. As reported in Table 1, adopting powers of 40 W and 100 W the temperature stabilizes to about 80 °C and 140 °C, respectively.

Preparations of samples for morphology investigations

For morphology investigations (FESEM and birefringence measurements), thin slices were cut out from molded samples by means of a Leica slit microtome at the cavity positions where pressure transducer P2 was located. Details of cutting procedures are illustrated in Fig. 3: thin slices were cut from the central part of the molded slab along flow direction (x) and parallel either to the flow-thickness plane (x, y) (sketch A) or to the flow-width plane (x, z) (sketch B).

Fig. 3 Cutting procedures of slices from molded samples for morphological investigations.

The same samples were subjected to analysis of morphology distribution along the thickness by means of optical microscopy and SEM analysis.

For each molded sample two optical micrographs of the cross section in position P2 are reported: (i) with the slice oriented along the direction of one of the polarizers direction; (ii) with the slices rotated of 45° with respect to the polarizers direction. Normally, the change of brightness during a 45° rotation is directly proportional to the material orientation level.

In order to better characterize morphological distribution in injection molded samples, slices already observed by means of optical microscopy, were chemically etched according to the procedure suggested by Bassett³¹ and then observed using both scanning electronic microscope. The etchant used was a solution of potassium permanganate in a mixture of 10 : 4 : 1 volumes of concentrated sulphuric acid, orthophosphoric acid and distilled water, respectively (1 g of potassium permanganate in 100 ml of mixture). A 2 h period of etching at room temperature was generally sufficient to reveal the surface topography. The samples were observed by a field emission-scanning electron microscope (FESEM, mod. LEO 1525, Carl Zeiss SMT AG, Oberkochen, Germany). Samples were coated with gold–palladium (layer thickness 250 Å) using a sputter coater (mod. 108 Å, Agar Scientific).

Birefringence

For quantitative birefringence gradient determination, the injection molded parts were microtomed (Fig. 3 sketch A) and placed between two glass slides and squeezed to eliminate any curling that may have developed during cutting. These samples were placed in a Leitz laborlux polarizing microscope under crossed polars. The local optical retardation values were determined using a Berek compansator (30 order) using appropriate magnification at series of locations from skin to skin. Each measurement location was determined by a linear calibration slide designed for such purpose for microscopes. Birefringence values were then determined by dividing retardation with local thickness of the sample determined by precision micrometer.
where Γ is retardation (with units of micrometers) and t is local thickness in micrometers.

X-ray

Wide-angle X-ray diffraction patterns, with nickel filtered CuKα radiation, were obtained, in reflection mode from the surfaces, with an automatic Bruker D8 Advance diffractometer. This analysis were performed on surface slices, 20 μm thick, cut on the cavity heated side as indicated in Fig. 3 sketch B.

X-ray patterns were analyzed by a deconvolution procedure performed according to a scheme reported in the literature³² and summarized below. The full spectrum is considered as a superposition of a number of reflections, due to each phase present (in this paper the diffraction peak related to the different crystalline phases are identified by the Miller indices³³); each reflection being described by a combination of a Lorentzian function and a Gaussian function.

The parameters defining each reflection were determined, with a general purpose optimization routine, adopting as objective function the total quadratic error with respect to the experimental spectrum.

The content of each phase in the samples was then calculated as

where A_i are the areas under selected peaks.

Results

Pressure evolution

Fig. 4(a) shows experimental pressure curves recorded in the four transducer positions P0–P3 for one representative experiment. In the figure, the instant at which the polymer reaches the transducer in pos. P2 is set to zero.

Fig. 4 (a) Experimental pressure curves obtained with a power surface of 40 W for a heating time t_h = 0.5 s, normally up to the filling, and labels P0–P3 in the figure identify the pressure transducer positions, namely in the injection chamber (P0), just before the gate (P1) and in the cavity (P2 and P3), as specified in Fig. 1. (b) Comparison between pressure evolution in pos. P2 for p_steel and p_100.8 tests.

During the filling stage, the pressure inside the injection chamber (P0) increases at first slowly, while the polymer fills the sprue and the runner and, due to the small thickness of both the gate and the cavity, with a faster pace after the polymer enters the gate. Fig. 4(a) shows that, once the mold was filled (with the parameters specified in Table 1), the packing stage was carried out at a constant pressure of about 300 bar; because there is still molten polymer both in the sprue and in the runner, pressure in position P1 follows the evolution of pressure in position P0. After gate freezing, the cooling starts with a progressive cavity pressure reduction in position P2. Pressure evolution downstream to the gate indicates that packing time is sufficient to maintain contact of the polymer with the mold in position P2. The comparison between the pressure profiles in position P2 for the test p_steel and for the test performed applying an electrical power of 100 W for 8 s is reported in Fig. 4(b). Although the heating time adopted for the test p_100.8 is very long, pressure in position P2 seems to be not affected by the heating phase. Similar results were obtained also at higher heating power. This is an interesting result since, as reported in literature,¹² with symmetric heating the heating phase generally gives rise to a reduction of the injection and packing pressures because the polymer is in the molten state for longer time. It has to be pointed out, however, that, for the tests performed in this work, the heating is not only asymmetric but it regards only a part of the cavity surface and a minor part of the downstream surface. However, a reduction of pressure as consequence of the surface heating (although asymmetric) was expected, evidently, with asymmetric heating there must be a compensating phenomenon for which the effect of the temperature of the cool side prevails as far as pressure drop.

Temperature profiles

For the tests considered in this work, the time, t_a, during which the heater is activated before the contact with the polymer in position P2 is held constant and equal to t_a = 2 s.

Six tests are selected for this work. Two of them were carried out without activating the heater. Whereas the other four experiments were performed activating the electrical heater with different power and heating time, t_h (time during which the heating element is held active, after the contact of the polymer on the mold at the position P2). The focus was on the effects of both the surface temperature evolution during the process and the morphology distribution in the final molded object.

In particular, as reported in Table 1, power of zero, 40 W and 100 W were supplied to the heating system and the values 0.5 s and 8 s were selected for the heating time, t_h; 0.5 s corresponds to the filling of the whole cavity.

The evolution of surface temperature on the heated side of the cavity is reported in Fig. 5(a) and (b); each figure refers to a different heating power (either 40 W or 100 W) and reports the surface temperature evolutions recorded with each values of the heating time, t_h = 0.5 s and t_h = 8 s. The evolution of surface temperature for the experiment labeled “p_steel” in Table 1 is also reported in Fig. 5(a) and (b) for comparison; temperature evolution for the experiment p_passive is reported in Fig. 5(a).

Fig. 5 Temperature profiles in position P2 obtained at t_h = 0.5 s and 8 s, for two values of electrical power applied on the mold surface: (a) 40 W; (b) 100 W (see Table 1). Temperature in pos P2 for the experiment p_steel, when the heater is not present, is also reported for comparison.

Optical characterization

Temperature evolution on the mold surface has a relevant effect on the final solid sample morphology.

The optical micrographs on slices cut on the flow-thickness plane (sketch A in Fig. 3) were obtained with crossed analyzer and polarizer. The optical micrographs of the six samples listed in Table 1 performed with the flow direction oriented both parallel to the analizer and rotated of 45° with respect to it are reported in Fig. 6(a) and (b). Normally, the change of brightness during a 45° rotation is directly proportional to the material orientation level.

Fig. 6 Optical micrographs of the whole thickness of molded sample slices cut in position P2 according to sketch B of Fig. 3. Heating powers and times t_h are indicated above each micrograph. The alignment of the samples between crossed polarizers is reported on the bottom: ‘A’ represents the analyzer; ‘P’ represents the polarizer; ‘F’ represents the flow direction. The sample thickness is about 0.980 mm.

The optical micrographs reveal the morphology distribution typical of an injection molded semicrystalline sample, often referred to as skin-core morphology, characterized by the presence of a series of distinct regions: a thin, oriented skin layer; an oriented non-spherulitic zone (often referred as ‘shear layer’, the dark zone in micrographs reported in the right side of Fig. 6(b)); a spherulitic core with small orientation.

On the heated side of the molded samples, the shear layer thickness decreases for each heating power either by an increase of the time at a given temperature or for a given time with the increase of temperature. Furthermore, the sample obtained with a power of 100 W, held active for t_h = 0.5 s, has a shear layer thickness smaller than the sample obtained with the power of 40 W, held active for t_h = 8 s: in the temperature range considered, the effect of the surface temperature on the shear layer thickness was found to be more substantial than the effect of heating time. It was already reported that the thickness of the shear layer decreases with the surface temperature.^24,25,34

The thicknesses of the layers shown by the micrographs of Fig. 6 are summarized in Table 2.

Table 2 Layers thicknesses as shown by the micrographs reported in Fig. 6

	Skin layer thickness	Shear layer thickness unheated	Spherulitic layer thickness	Shear layer thickness heated	Skin layer thickness
p_steel	4.5%	27.6%	35.8%	27.6%	4.5%
p_passive	3.4%	32.4%	31.1%	28.1%	5%
p_40.05	0.5%	33.0%	38.3%	23.2%	5%
p_40.8	0%	33.0%	43.0%	19	5%
p_100.05	0.1%	35.8%	49.3%	9.8%	5%
p_100.8	0%	32.6%	51.4%	10.0%	6%

---

FESEM analysis

A more detailed analysis of morphology distribution along the thickness was carried out by FESEM analysis. Selected FESEM micrographs have been assembled together with the aim of representing the main morphological features in a single figure.

The p_steel sample was injection molded with the two equivalent cavity surfaces, as far as temperature and thermal properties; indeed the morphology distribution was found symmetric and it is represented by five micrographs in Fig. 7.

Fig. 7 Morphology distribution along the thickness of slices cut according to sketch A Fig. 3 of the sample p_steel. The number of fibrillar elements per length () and the spherulitic diameter () are reported vs. the position along the thickness.

A clearly spherulitic structure was detected in the central zone, structures aligned along the flow direction were observed in the shear layers, two different morphologies were identified in each skin layer (see also Table 2). In particular elongated structures aligned parallel to the mold surface were detected in a very thin (less than 10 μm) layer on the surface, and thin interconnected structures were observed in a layer (of about 50 μm thickness) adjacent to the previous one. In particular, in this layer globular elements appear randomly dispersed in a network of nano-structures having thickness of the order of 10 nm, in the following this morphology is denoted as “nano-aggregate network” morphology.

Adjacent to this “nano-aggregate network” morphology, starts the shear layer where fibrillar structures are aligned along the flow direction. A plot of the number of fibrillar like structures per unit length is also reported in Fig. 7; obviously, the number of fibrillar like structures per unit of length is zero in the spherulitic central layer and also in the 50 μm layer where nano-aggregate network were observed. Furthermore the width of the skin, shear and core layers is consistent with those shown in Fig. 6 and reported in Table 2.

From Fig. 8 to 11 the morphology of the other four samples (heated asymmetrically with power of 40 W and 100 W for t_h = 0.5 s and t_h = 8 s) is reported. Main differences of these figures with respect to the p_steel case, Fig. 7, are:

Fig. 8 Morphology distribution along the thickness of slices cut according to sketch A (Fig. 3) of the sample p_40.05. The number of fibrillar elements per length is reported vs. the position along the thickness.

Fig. 9 Morphology distribution along the thickness of slices cut according to sketch A (Fig. 3) of the sample p_40.8. The number of fibrillar elements per length is reported vs. the position along the thickness.

Fig. 10 Morphology distribution along the thickness of slices cut according to sketch A (Fig. 3) of the sample p_100.05. The number of fibrillar elements per length is reported vs. the position along the thickness.

Fig. 11 Morphology distribution along the thickness of slices cut according to sketch A (Fig. 3) of the sample p_100.8. The number of fibrillar elements per length is reported vs. the position along the thickness.

• The asymmetry of the morphology distributions (in scale with the asymmetry of the thermal boundary conditions on the two cavity surfaces).

• The thin layer with thin interconnected structures (of about 50 μm thickness in Fig. 7, the dark layer in the micrographs of Fig. 6) was not found on the heated side of the samples.

Fig. 8 and 9 show the morphology distribution of the samples obtained using an electrical power of 40 W heating the mold surface for t_h = 0.5 s and 8 s respectively.

The number of fibrillar like structures aligned per unit length on the heated mold surface for the sample p_40.05, considered in Fig. 8, was again similar to that of the p_steel sample. However, rather than the sharp morphology change shown by the sample p_40.05 within a few microns, a gradual decrease of the number of structures per unit length toward a value about one half of that of the p_steel sample in the shear layer was observed. This can be synthesized as follows: the shear layer reaches the sample surface and the number of fibrillar elements per unit length increases close to the surface.

A sharp transition from a very thin (a few microns) skin layer (with a number of fibrillar structures per unit length similar to that of the p_steel sample) to the shear layer is shown in Fig. 9 for the heated side of the sample p_40.8. The shear layers on the heated side of the p_40.8 sample becomes a little thinner with respect to the sample obtained with heating time of 0.5 s and the number of fibrillar like structures per unit length is close to that in the shear layer in the heated side of the sample p_40.05. On the unheated side of the sample, the shear layer retains essentially the same thickness and, closer to the surface, a layer (of about 20 μm thick) with morphology similar to the one shown for p_steel sample (namely the “nano-aggregate network” morphology) was detected.

The morphology distributions of the samples obtained with heating power 100 W are showed in Fig. 10 and 11.

The features observed for these samples are qualitatively similar to those observed in the samples obtained with heating power 40 W. In particular, on the heated side very thin layers, with quite high number of fibrillar elements per unit length, were detected. Adjacent to the surface, shear layers thinner than those observed with heating power of 40 W and with smaller number of fibrillar like structures adjacent to the heated surface were identified. In the unheated side, between the surface and the shear layer, thin layers (10–20 μm thick) with nano-aggregate network morphology, were found. The shear layers have fibrillar element densities smaller than the samples heated with 40 W. Furthermore, shear layer thicknesses on the heated side and the fibrillar element density was found to decrease with the heating time (from 0.5 s to 8 s).

For all the samples, the layer thicknesses are consistent with those shown by optical micrographs in Fig. 6 and reported in Table 2.

It is also interesting to remark the morphology observed in the spherulitic-shear transitional region. The p_steel sample shows shish-kebab morphology in both the transitional areas, since symmetrical thermal conditions were set to produce this sample. A similar behavior could be observed for the samples p_40.05, p_40_8 and p_100.05 on both (heated and unheated) sides of the spherulitic layer. For the sample p_100.8 a significant reduction of shish-kebab density was detected on the heated side (no reduction of shish-kebab density was detected on the unheated side); the effect on the heated side should be related to their molecular orientation and stretch relaxation before crystallization. Indeed, the amount of orientation and stretch relaxation is determined by comparison between the relaxation time and residence time at temperatures higher than the crystallization temperature.

Birefringence

The birefringence distribution along the thickness, on the flow direction plane (position P2) is reported in Fig. 12 and 13. Each of the two figures regards one of the two heating powers (40 W, 100 W) adopted to increase the mold surface temperature; the data of p_steel sample are reported for comparison in each of the two figures.

Fig. 12 Birefringence of the molded obtained at a power density of 40 W (80 °C) for different t_h. Birefringence of the molded obtained at 25 °C is also reported for comparison. () p_steel; () p_40.05; () p_40.8.

Fig. 13 Birefringence of the samples obtained at a power density of 100 W (140 °C) for different t_h. () p_100.05; () p_steel; () p_100.8. Birefringence of the molded obtained at 25 °C, p_steel is also reported for comparison.

The birefringence is a measure of the local molecular orientation averaged over crystalline and amorphous domains, thus one expects to find asymmetric distribution along the thickness, when the thermal boundary condition in the cavity is not symmetrical. Indeed, all curves, reported in Fig. 12 and 13, have an asymmetric character, except for the p_steel sample. Furthermore, for each curve, the values of the birefringence are larger on the unheated side than in the heated side, especially when an electrical power of 100 W is set, which corresponds to the expectation of the distribution of molecular stretch and orientation.

The values of birefringence can be adopted also to compare molecular stretch and orientation of different samples, thus they can help in interpreting the morphology distributions reported in Fig. 7 to 11.

In particular, smaller values of birefringence indicate locally smaller orientation and molecular stretch and vice versa. Fig. 14 shows a comparison between the birefringence and the number of fibrillar like structure per length for the sample p_steel.

Fig. 14 Comparison between birefringence and number of fiber per length for the p_steel sample. () birefringence; () number of fibrillar element per length.

A comparison of the distributions of birefringence with the curve of fibrillar density detected on the p_steel sample shows that the two curves have a very close pattern and analogous observation can be extended to birefringence and density of fibrillar elements of all samples analyzed in this work. Thus the transitions from one morphology to another can be related to a value of the birefringence (obviously for that material); for instance to a first approximation the spherulitic morphology seams to correspond to a birefringence smaller than about 0.00025 and where birefringence was found larger than about 0.00035, the fibrillar like structures were detected. Furthermore, the comparison of the data of Fig. 7 to 11 with those in Fig. 12 and 13 shows that larger values of birefringence are related to larger values of fibrillar density.

X-ray characterization

X-ray analysis were performed by reflection on the heated side of the molded samples, the purpose of the analysis was mainly that of correlating the orientations at the samples surfaces to mold surface heating power (temperature) and heating time t_h.

Fig. 15(a) and (b) compares the X-ray diffraction profiles: obtained with different heating powers and heating times.

Fig. 15 X-ray spectra of the heated sample surface in pos. P2. (a) Spectra of the samples obtained at 40 W (80 °C) and different t_h; (b) spectra of the samples obtained at 100 W (140 °C) and different t_h.

The diffraction profiles show that the peaks α110, α040 and α130 (2θ = 14, 16.6 and 18.5), that are related to the α-PP crystallites, have a higher intensity at lower mold temperature (80 °C) and lower heating time t_h.

Trotignon et al.³⁵ defined the orientation index A₁₁₀ and A₁₃₀; these indices characterize the degree of orientation of α-PP crystallites. The determination of both indices is based on the vanishing (or decrease of intensity) of the reflections α111 and α131 + 041 in the equatorial measurement when the crystallites are oriented along the of flow direction; (hence A = 1 for highly oriented α-crystallites, otherwise A < 1). These indices are defined as follows:

where I is the intensity of each peak. Table 3 shows the surface orientation indices obtained with different heating powers (surface temperatures) temperature and heating times t_h.

Table 3 Orientation indices and crystalline percentage of the samples obtained at different t_h and mold temperature

	A110	A130	Cryst%
p_steel	0.98	0.97	58
p_40.05	0.98	0.96	61
p_40.8	0.95	0.91	59
p_100.05	0.98	0.95	61
p_100.8	0.82	0.69	55

---

The values of A₁₁₀ and A₁₃₀ indices of the samples obtained at t_h = 0.5 s are close to those of the p_steel sample. A small decrease of the indices takes place by increasing the heating time to 8 s especially with the higher power (100 W). As expected the orientation on the skin decreases at (higher temperature and longer t_h), namely when the relaxation time decreases and there is more time to relax the molecular stretch and orientation.

Also the crystallinity of the samples was determined from the diffractometer profiles and they are similar to those obtained in a previous work.²⁵ In this case, the crystallinity is affected by the orientation of the samples. Indeed, more oriented samples show a higher crystalline percentage, accordingly with results reported in literature.³⁶ This behavior is due to the increase of the crystallization kinetic by the effect of molecular orientation and stretch.

Discussion of the results

The process

The surface temperature evolutions, reported in Fig. 5(a) and (b), show that with an electrical power of the order of 10 W cm⁻², the mold surface temperature can be raised to above 100 °C, in a time of the order of one second. An additional significant temperature increase, of about 50–60 °C, is determined by the contact with the incoming melt.

Obviously, also the other steps of the process have to be considered because once the cavity is filled the polymer has to undergo solidification of most of its thickness before being ejected. Thus, the wall temperature during filling is important, but very important is also the increase of the cooling time. Cooling time certainly depends upon the electrical/thermal insulating layer (red in Fig. 2) between the electrical resistance and the mold, which in this work was chosen with a large thickness to avoid thermal dissipation through the mold. The temperature evolutions of the p_steel and p_passive samples are reported in Fig. 5(a) for comparison; it is worth pointing out that the cooling rate in the case of p_passive experiment is decreased by the heat transfer resistance due to all layers shown in Fig. 2, also when the electrical heating is not activated (p_passive).

The temperature evolutions reported in Fig. 5(a) and (b) show that, as soon as the maximum temperature was reached on the surface, about 150 °C and 210 °C for a power of 40 W and 100 W respectively, the temperature immediately starts to decrease very fast and, when the heating element is turned down at t_h = 0.5 s, the cooling rate immediately increases: cooling rate was about 60 °C s⁻¹ and 120 °C s⁻¹ for the applied electrical powers of 40 W and 100 W, respectively. The comparison between the cooling evolution of the p_steel sample and of the sample p_40.05 shows that the time required to the sample p_40.05 to reach 50 °C at the surface, which is a reasonable ejecting temperature, is about 3–4 s longer than the time the p_steel sample takes to cool down to the same temperature and less than 1 s longer than the time required by p_passive sample. Therefore, the thermal insulating layer (the 140 μm red layer in Fig. 2) is the main cause for the cooling time increase. It is certainly possible to reduce the thickness of this layer; however, this solution implies the increase of the electrical power necessary to reach the same heating rate reached during the experiments proposed in this paper. In any case, the cooling time increase obtained using the heater device proposed in this paper is already a good result in comparison to results of temperature evolutions previously reported in the literature and discussed in the introduction and, obviously, with respect to the hypothesis of carrying out the whole process at high temperature.

It may be worth pointing out here that asymmetric thermal boundary conditions determine also a modification of the flow field, which will be faster on the hotter side.¹⁶ Obviously, the modification would be in scale with the thermal asymmetry.

In the result section, it was shown that the asymmetric heating determines asymmetric morphology distribution. The data shown in Fig. 7 to 13 and in Table 3 are further analyzed below and the mechanisms regulating final morphology distribution are discussed.

Morphology distribution

The molecular orientation and stretch of the melt is the result of a competition between the characteristic relaxation time of the polymer, that is function of thermo-mechanical history, and the flow characteristic time, that is the reciprocal of the deformation rate.^37,38 High orientation/stretch levels can be reached when the ratio between the flow characteristic time and the relaxation time is high.^{24,25,28–30,39} When an oriented/stretched melt is cooled down, the residual orientation in the melt is determined by the competition between relaxation time (which is function of temperature and molecular stretch) and cooling time down to crystallization temperature, which is the temperature at which crystallization time is of the same order of the cooling time through the crystallization temperature interval. Local morphology is determined by the molecular orientation and stretch during crystallization and by the molecular relaxation time in comparison to crystallization time toward the preferred crystalline phases at that temperature and pressure.³⁷

With reference to the morphology distribution along the thickness of molded samples, the effect of filling flow on melt orientation and stretch is very low in the central zone if the flow is symmetric and, for thermally asymmetric cases, the zone with low melt orientation and stretch moves toward the large temperature side.¹⁶ Thus, in these zones, the melt gains small molecular orientation and stretch during filling and this orientation undergoes some relaxation during cooling, with the result of final spherulitic structures.

In the symmetric p_steel sample, different morphologies were observed from the central spherulitic zone to the sample surface: a shear layer with fibrillar elements aligned along the flow direction, an intermediate zone of about 50 μm thickness, with thin interconnected structures, namely nano-aggregate network, and finally a very thin layer, of the order of 10 μm, with elongated structures aligned parallel to the mold surface. It is generally agreed^24,25 that the 10 μm layer is due to the very fast cooling which freezes the high molecular stretch determined by the fountain flow during filling; the melt arriving in the 50 μm layer (nano-aggregate network) is oriented and stretched to a smaller extent by the effect of the fountain flow and it is also quenched with the fountain flow molecular orientation and stretch level, which is smaller than that necessary to give rise to aligned elongated structures but too large for crystallizing into a spherulitic morphology; the result is the intermediate structure shown in the FESEM micrograph of Fig. 7 and also to a smaller extent on the un-heated side of the samples obtained at an electrical power of 40 W and 100 W. Fig. 8 to 11 show the shear layer thickness reduction, due to the combined effect of temperature and shear rate determined by the temperature increase on the heated side of the cavity.

The development of morphology on the heated side is modified with respect to the p_steel sample because on that side the temperature is held higher with respect to the symmetric p_steel case; the higher temperature has a different effect on each of the three layers of the heated side.

In spite of the surface temperature increase, the 10 μm first layer at the surface still crystallizes as soon as it arrives on the surface, because its crystallization rate is enormously enhanced by the effect of the molecular stretch determined by the fountain flow, and its morphology does not change because crystallization rate does not allow relaxation of molecular stretch. This picture is consistent with the X-ray diffraction patterns on the heated surface, since, the orientation (A₁₁₀ and A₁₃₀ indices, see Table 3) does not significantly change for the samples p_40.05, p_40.8 and p_100.05, respect to the p_steel sample, and a small orientation reduction could be measured for the sample p_100.8. Soon beyond the first layer the polymer does not crystallize immediately because cooling rate, molecular stretch, crystallization kinetics all decrease and the polymer, still in the molten state, can undergo filling shear deformation which determines an increase of molecular stretch sufficient to give rise to the formation of fibrillar elements aligned along the flow direction: as a consequence the shear layer impinges on the surface layer and the intermediate layer disappears. On the other hand, until crystallization does not take place, the molecular orientation and stretch decrease because of the relaxation, due to the higher temperature and in addition to longer heating. As a result the birefringence of the shear layers decreases with both the heating power and the heating time; also the density of fibrillar elements shows a decreases in the shear layers with their relaxation. Obviously, as the relaxation increases, the thickness of the shear layers decreases; this is clearly shown by both the birefringence and the fibrillar density paths.

Also the morphology observed in the spherulitic-shear layers transition regions is interesting. In this area shish-kebab morphology was detected for all the samples analyzed, except for the sample p_100.8, wherein the shish-kebab morphology was not detected. The shish-kebab superstructure is a composition of fibrillar like entities (the “shish”) with the “kebabs” entities perpendicularly crystallized on the fibrillar structures upon an epitaxial growth. The formation of this kind of structures is object of extensive investigations.^40–43 The shish formation is attributed to the presence of long chains that can be easily oriented at temperatures above the melting point.^44,45 The resulting metastable, non crystalline aggregations of polymer chains act as primary nuclei for the oriented structures during cooling. Segments of the oriented crystallized chains, in its turn, act as nuclei for the formation of perpendicular layered crystalline lamellae (kebabs).

The extensive formation of kebabs depends upon a fine balancing between local chains mobility (which, in its turn, depends upon temperature but also upon thermo-mechanical history) and time available under that mobility; obviously the kebabs can grow if there is space between the shishs.

Sometime, the formation mechanism is aided by the presence of short chains that epitaxially crystallize on the lateral side of longer chains crystallized into shish.^46–48 Probably, the iPP used in this work has a molecular weight distribution wide enough to allow a significant formation of shish-kebab.

The density of fibrils over the thickness of an injection moulded object is function of local molecular orientation and stretch; fibril density decreases and the space between two adjacent fibrils increases as one moves from the interior of a fibrillar zone toward the fibrillar/spherulitic transition. Somewhere along this path there must be enough space, but there the molecular mobility has to be sufficient to let the molecules to crystallize into kebabs in the time available after the shish formation and before the material cools trough temperatures where crystallization rate becomes negligible. According to this picture, cooling rate in the transition region is very important, as high cooling rates are expected to prevent the kebab formation and vice versa. Indeed, kebabs were detected in all transition regions except for the sample p_100.8 which has the transition region closer than all the others to the surface and it is expected to undergo a faster cooling during crystallization.

Conclusions

Fast mold surface temperature evolution during the injection molding process was driven by the Joule heating effect in a thin layer just below the cavity surface. Only one of the two cavity surfaces was heated and the first contact temperature of that surface with the molten polymer was brought up to 160 °C. With a first contact temperature of about 90 °C, cooling time increase was only of a few seconds.

The optical microscopy showed that, on the heated side of the mold, the shear layer thickness clearly decreases with both the surface heating power and the heating time, whereas, the shear layer thickness on the unheated side remains almost the same; consequently the spherulitic layer thickness undergoes a clear increase with the same heating parameters.

In particular, for the sample injected without any surface heating, a morphology characterized by small molecular orientation and stretch was observed in a 50–60 μm layer located between the shear layer and a very oriented thin (10 μm) layer at the surface, this morphology was called nano-aggregate network. This morphology disappeared on the heated side of the samples asymmetrically heated during the process, in these cases the shear layers impinged on the heated surface.

The formation of all the detected morphologies has been explained on the basis of a progressive relaxation within the melt with heating power and time. The formation of the nano-aggregate network morphology has been ascribed to the instantaneous solidification close to the cool surface, which hinders the enhancement of orientation due to the shear flow. If the surface temperature is such that at the surface the polymer can be sheared before solidification, the new nano-aggregate network morphology disappears and the shear layer impinges on the surface.

The shish-kebab morphology was detected in most of the transition regions between spherulitic and fibrillar morphologies. The observation that kebabs were not detected for the sample injected with high heating power and time, that means 140 °C on mold surface for 8 s, was explained on the basis of the fact that the transition region being very close to the mold surface underwent a fast cooling which did not leave sufficient time for the kebab formation.

The local number of fibrillar elements per unit length was detected and plotted against the distance from the surface for all samples. The resulting plots were found to have paths similar to the birefringence distribution along the thickness. Therefore, a strong relationship between the orientation and the number of fibrillar elements per length exists, and this result is very important as it could be applied to predict the morphology of molded and could be brought to the injection molding of other semicrystalline thermoplastic polymers.

References

1. M. Burgsteiner, F. Muller, T. Lucyshyn, C. Kukla and C. Holzer, Proceedings of Pps-29: The 29th International Conference of the Polymer-Conference Papers, 2014, vol. 1593, pp. 183–188.
2. G. Lucchetta, M. Fiorotto and P. F. Bariani, Cirp Annals-Manufacturing Technology, 2012, vol. 61, pp. 539–542.
3. U. M. Attia, S. Marson and J. R. Alcock, Microfluid. Nanofluid., 2009, 7, 1–28.
4. P. Y. Song, R. Hu, D. J. H. Tng and K. T. Yong, RSC Adv., 2014, 4, 11499–11511.
5. U. A. Theilade and H. N. Hansen, Int. J. Adv. Des. Manuf. Technol., 2007, 33, 157–166.
6. A. C. Liou and R. H. Chen, Int. J. Adv. Des. Manuf. Technol., 2006, 28, 1097–1103.
7. B. Yalcin and M. Cakmak, Polymer, 2004, 45, 2691–2710.
8. C. M. Hsiung, M. Cakmak and Y. Ulcer, Polymer, 1996, 37, 4555–4571.
9. M.-S. Huang, C.-J. Li, J.-C. Yu, Y.-M. Huang and L.-C. Hsieh, J. Mater. Process. Technol., 2009, 209, 5690–5701.
10. R. Wimberger-Friedl, Specialized Molding Techniques: Application, Design, Materials and Processing, 2008, p. 149.
11. U. M. Attia and J. R. Alcock, Int. J. Adv. Des. Manuf. Technol., 2010, 50, 533–542.
12. M. C. Jeng, S. C. Chen, P. S. Minh, J. A. Chang and C. S. Chung, Int. Commun. Heat Mass Transfer, 2010, 37, 1295–1304.
13. G. L. Wang, G. Q. Zhao, H. P. Li and Y. J. Guan, Mater. Des., 2010, 31, 382–395.
14. S. C. Chen, W. R. Jong and J. A. Chang, J. Appl. Polym. Sci., 2006, 101, 1174–1180.
15. S. C. Chen, W. R. Jong, J. A. Chang and Y. J. Chang, Int. Polym. Process., 2006, 21, 457–463.
16. S. C. Chen, Y. Chang, Y. P. Chang, Y. C. Chen and C. Y. Tseng, Int. Commun. Heat Mass Transfer, 2009, 36, 1030–1035.
17. P. C. Chang and S. J. Hwang, Int. J. Heat Mass Transfer, 2006, 49, 3846–3854.
18. M.-C. Yu, W.-B. Young and P.-M. Hsu, Mater. Sci. Eng., A, 2007, 460, 288–295.
19. D. G. Yao, T. E. Kimerling and B. Kim, Polym. Eng. Sci., 2006, 46, 938–945.
20. K. Jansen and A. Flaman, Polym. Eng. Sci., 1994, 34, 894–897.
21. S. Liparoti, D. Sofia, A. Sorrentino and G. Titomanlio, Rapid Mold Surface Temperature Evolution During Injection Molding Process: Morphology Dependence on Electrical Power and Heating Time Presented at PPS2014 Europe-Africa PPS Conference, Tel-Aviv, Israel, 2014.
22. J. Braz, S. Liparoti, M. Cakmak and G. Titomanlio, Control of Morphology of Injection Molded Objects by Rapid Mold Surface Temperature Evolution, in 6th International Conference on Polymers and Moulds Innovations, ed. A. J. Pontes and A. S. Pouzada, University of Minho, Guimarães, 2014.
23. S. Liparoti, T. M. Hunag, A. Sorrentino, G. Titomanlio and M. Cakmak, Rapid control of mold temperature during injection molding process, Presented at 30th International conference of Polymer Processing Society, Cleveland, Ohio, USA, 2014.
24. I. Coccorullo, R. Pantani and G. Titomanlio, Int. Polym. Process., 2005, 20, 186–190.
25. R. Pantani, I. Coccorullo, V. Speranza and G. Titomanlio, Prog. Polym. Sci., 2005, 30, 1185–1222.
26. R. Pantani, V. Speranza, I. Coccorullo and G. Titomanlio, Macromol. Symp., 2002, 185, 309–326.
27. R. Pantani, V. Speranza, A. Sorrentino and G. Titomanlio, Macromol. Symp., 2002, 185, 293–307.
28. I. Coccorullo, R. Pantani and G. Titomanlio, Polymer, 2003, 44, 307–318.
29. R. Pantani, I. Coccorullo, V. Volpe and G. Titomanlio, Macromolecules, 2010, 43, 9030–9038.
30. R. Pantani, V. Speranza and G. Titomanlio, Macromol. Theory Simul., 2014, 23, 300–306.
31. H. M. White and D. C. Bassett, Polymer, 1998, 39, 3211–3219.
32. N. S. Murthy and H. Minor, Polymer, 1990, 31, 996–1002.
33. P. Zipper, A. Janosi, W. Geymayer, E. Ingolic and E. Fleischmann, Polym. Eng. Sci., 1996, 36, 467–482.
34. R. Cermak, M. Obadal, P. Ponizil, M. Polaskova, K. Stoklasa and A. Lengalova, Eur. Polym. J., 2005, 41, 1838–1845.
35. J. Trotignon, J. Lebrun and J. Verdu, Plastics and Rubber Process. and Applic., 1982, vol. 2, pp. 247–251.
36. G. Kalay and M. J. Bevis, J. Polym. Sci., Part B: Polym. Phys., 1997, 35, 265–291.
37. Y. Koike and M. Cakmak, Macromolecules, 2004, 37, 2171–2181.
38. Y. Konishi and M. Cakmak, Polymer, 2005, 46, 4811–4826.
39. A. Sorrentino and R. Pantani, Polym. Bull., 2013, 70, 2005–2014.
40. R. H. Somani, L. Yang, B. S. Hsiao, T. Sun, N. V. Pogodina and A. Lustiger, Macromolecules, 2005, 38, 1244–1255.
41. J. K. Hobbs, Polymer, 2006, 47, 5566–5573.
42. L. B. Li and W. H. de Jeu, Interphases and Mesophases in Polymer Crystallization Ii, 2005, vol. 181, pp. 75–120.
43. L. Wang and M.-B. Yang, RSC Adv., 2014, 4, 25135–25147.
44. R. H. Somani, L. Yang, B. S. Hsiao, P. K. Agarwal, H. A. Fruitwala and A. H. Tsou, Macromolecules, 2002, 35, 9096–9104.
45. G. Reiter and G. R. Strobl, Progress in understanding of polymer crystallization, Springer Science & Business Media, 2007.
46. Y. Ogino, H. Fukushima, N. Takahashi, G. Matsuba, K. Nishida and T. Kanaya, Macromolecules, 2006, 39, 7617–7625.
47. R. H. Somani, L. Yang and B. S. Hsiao, Polymer, 2006, 47, 5657–5668.
48. G. Matsuba, S. Sakamoto, Y. Ogino, K. Nishida and T. Kanaya, Macromolecules, 2007, 40, 7270–7275.

---