Synthesis, crystal structures, magnetic properties and DFT calculations of nitrate and oxalate complexes with 3,5 dimethyl-1-(2′-pyridyl)-pyrazole-Cu(ii)†
Abstract
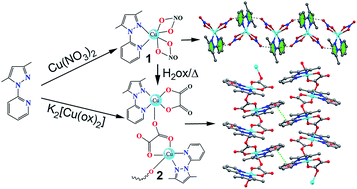
The synthesis, crystal structures and magnetic property of an uncommon oxalate-containing copper(II) chain of formula [Cu(L)(Ox)2(H2O)]n (2), where L = 3,5 dimethyl-1-(2′-pyridyl)-pyrazole and a mononuclear Cu(II) complex [Cu(L)(NO3)2] (1) derived from the same ligand, which can be used as the precursor of compound 2 are reported. The structure of 2 consists of tridentate oxalate-bridged (μ1,2,3) copper(II) chains, ligand (L) and crystallization water molecules. Variable-temperature magnetic susceptibility measurements of 2 show the occurrence of a weak ferromagnetic interaction through the oxalate bridge [J = +1.95 ± 0.08 cm−1]. The small J value can be interpreted as a consequence of the almost zero overlap between the Cu(II) ions through the bridging ligand due to the different character (axial and equatorial), giving quasi-orthogonal magnetic orbitals. DFT calculations have been used to rationalize several aspects including the magnetic coupling mechanism and the interesting noncovalent interactions observed in the solid state architecture of compounds 1 and 2.


 Please wait while we load your content...
Please wait while we load your content...