Preparation and assembly of concave polymer microparticles

Abstract

This report proposed a promising method that combined microfluidic techniques, phase separation and selective dissolution to prepare uniform concave polystyrene (PS) microparticles. Monodisperse emulsion droplets containing PS and poly(methyl methacrylate) (PMMA) in chloroform were firstly obtained using a microcapillary-based microfluidic device. Uniform PS/PMMA Janus composite particles were then generated through the phase separation between PS and PMMA within the emulsion droplets during organic solvent evaporation. Subsequently, uniform PS concave particles were obtained through selective dissolution of the PMMA domain in the Janus composite particle with acetic acid. Moreover, depletion-mediated directional self-assembly of the prepared concave PS particles was investigated, and polymeric worm-like chains with head-to-tail configuration were observed.

---

Introduction

In the past decade, substantial effort had been invested to fabricate non-spherical particles in many ways such as cubic colloids through silica deposition on colloidal hematite templates,¹ triangular particles by seeded emulsion polymerization,² bowl-shaped particles (or dimpled particles) via a hybrid of template-assisted method and controlled deformation,^3–7 or through a temperature-controlled swelling process,⁸ ellipsoids by microfluidics,⁹ and polyhedral particles using the polyol method.^10,11 Compared with spheres, non-spherical particles with anisotropic shapes could enhance their self-organization behaviours,^12–14 and open unique opportunities for applications such as rod-shaped particles enhancing antibodies specificity and avidity in therapeutics and diagnostics,¹⁵ mesoporous silica ellipsoids used as carriers for drug delivery,¹⁶ and a gold nanobowl array serving as a universal surface-enhanced Raman scattering substrate with the high surface-enhanced Raman scattering enhancement factor.¹⁷

Many novel self-assembled structures can be formed because of anisotropic shape of non-spherical particle. In experiments, round corner cubes self-organized into cubic crystals and convex octahedral particles formed an exotic superstructure with complex helical motifs, which were both directed by depletion attraction.^1,11 Without any attractive interaction, bowl-like particles were demonstrated to stack into columnar liquid crystalline phases driven by entropy alone.⁴ Moreover, in external electrical field, bowl-like particles tended to organize into chains with open cavities arranged perpendicularly to the field.^5,18 Flattened particles assembled into colloidal chains or doublets in the presence of moderate ion strength when no external field was applied.^19,20 While in simulations, Damasceno et al. investigated 145 convex polyhedra and then predicted the self-assembled structure of a given polyhedron: a liquid crystal, plastic crystal, or crystal.¹³ Self-assembled phase diagram of colloidal hard superballs directed by entropy alone was demonstrated, and in that work the shapes of superballs changed from cubes via spheres to octahedral.²¹ Interactions among particles relative to shapes of particles also had an effect on the aggregated structures of particles. Stacking structures of bowl-shaped particles mediated by depletion interaction and by entropy were studied separately, yet their self-assembled structures were not in complete accord.^22,23 Notably, particles were shown to self-assemble into various structures, which depended strongly not only on their geometrical shapes but also on interactions among them, and the self-assembled structures can be accurately predicted and controlled; thus, it is fundamental and critical to fabricate non-spherical particles for systematic investigation of their phase behaviours.

Here, we propose a versatile approach to fabricate uniform, non-spherical building blocks with concave shapes by combining microfluidics, solvent evaporation and selective dissolution. Monodisperse droplets containing binary mixtures of polystyrene (PS) and poly(methyl methacrylate) (PMMA) were firstly generated through microfluidics.^24–26 Gradual evaporation of organic solvent triggered phase separation between PS and PMMA within the droplets to form heterogeneous Janus particles. Concaved particles were then obtained through selective dissolution of one phase in Janus particles. Compared with the reported strategies for fabrication of non-spherical particles, our approach is more facile and provides more ability in the control over shape, size, and size distribution of particles. Based on the resulting concaved PS microparticles with tunable shape and sizes, the self-organization of concaved particles induced by depletion interaction were further explored via introducing poly(ethylene oxide) (PEO) to the system.

Results and discussion

Capillary microfluidic device was used to prepare monodisperse emulsion droplets with well-defined sizes, as illustrated in Fig. 1.²⁷ Typically, oil phase and water phase consisted of PS/PMMA/chloroform solution and SDS aqueous solution, respectively. Generally, emulsion droplets can be formed at the orifice of the channel due to the shearing force and interfacial tension of oil phase–water phase. Through this technique, emulsion droplets with uniform sizes can be generated and the overall size of the emulsion droplets could be easily controlled by varying the shearing force of the continuous fluid and/or flow ratios of the dispersed phase and continuous phase.

Fig. 1 (a) Schematic description of a capillary-based microfluidic device with a flow focusing geometry. The disperse phase and continuous phase flow from the opposite directions in a square capillary and these two phases are collected and exit through circular orifice, which results in the formation of droplets flowing down collection tube. (b) Optical microscopy image of the formation of monodisperse emulsion droplets in orifice flowing downstream.

In the next stage, chloroform in PS/PMMA emulsion droplets was evaporated at room temperature. As chloroform released from emulsion droplets to continuous phase during incubation, the binary mixture of PS and PMMA dissolved in the droplets was concentrated, leading to the phase separation.^28,29 Fig. 2 shows the optical microscopy images and SEM photographs of PS/PMMA composite particles. The phase diagram of PS/PMMA/chloroform indicated that the amount of chloroform in the PS-rich phase was less than that of PMMA-rich phase and this partition ratio of chloroform would not change until the end of solvent evaporation.³⁰ Because chloroform content in the PMMA-rich microdomains was higher than that in PS domains, PS phase was hardened before PMMA phase. When the PS phase solidified, the PMMA phase still contained some solvent and it therefore continued to shrink on solvent extraction, resulting in the formation of microparticles composed of two distinct compartments.^31,32 The difference in distribution of chloroform in PS phase and PMMA phase could be interpreted based on the polymer–solvent interaction parameter χ_PS (P = polymer and S = solvent). According to the Flory–Huggins criterion, when the value of χ_PS is less than 0.5, solvent and polymer are completely miscible, and the smaller the value is, the stronger the affinity between solvent and polymer is. The value of χ_PS–CHCl3 is 0.45 and the value of χ_PMMA–CHCl3 is 0.39; that is, the affinity between chloroform and PMMA is stronger than that between chloroform and PS,^31,33 which will greatly influence the morphology of the composite particles. Okubo et al. discussed the effect of colloidal stabilizer on the shape of PS/PMMA composite particles prepared in aqueous medium by solvent evaporation method. They found that when SDS was used as a colloidal stabilizer, the shapes of the obtained particles changed from dent, via snowman-like, to spherical with the increase of SDS concentration, which was explained from that the interfacial tensions between PS and PMMA phases and aqueous solution approached one another with increasing SDS concentration.²⁸ The adsorption of SDS molecule on the surfaces of particles significantly decreased the interfacial intensions between polymers and water, and the adsorption of SDS molecules is heterogeneous among particle surfaces. The Gibbs free energy change (ΔG) for structural development during phase separation can be attributed to the interfacial free energy variation, and the shape having the minimum ΔG is the thermodynamically most stable. Thus, the shapes of PS/PMMA composite particles in our experiments were the most stable morphology at SDS concentration of 3 mg ml⁻¹.

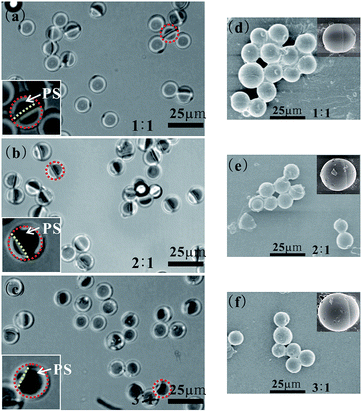Fig. 2 Optical microscopy images (a–c) and scanning electron microscopy (SEM) images (d–f) of PS/PMMA Janus particle. The dark region in a single particle in optical microscopy images was PS domain, because the refractive index of PS is larger than that of PMMA. In panels (a–c), red dashed rings circled typical Janus particles and insets are the enlarged views of these Janus particles, and yellow dashed line displayed the phase interfaces between PS phase and PMMA phase. The mean diameters and size distributions are (a) d = 11.84 μm and CV = 7.9%, (b) d = 12.03 μm and CV = 11.7%, (c) d = 12.02 μm and CV = 10.9%, respectively. CV was calculated as the standard deviation of the diameter of particle divided by the mean diameter.²⁶

The influence of concentrations and components of oil phases on the size and particle size distribution (PSD) of Janus particles were also demonstrated. For component, PS synthesized through dispersion polymerization (PVP served as dispersant), some of the steric stabilizer can be grafted on PS particles via hydrogen abstraction.³⁴ Size and PSD of composite particles changed insignificantly (Fig. 3c, d, g, h, k and l and S1†), which clarified that solubility of PS in chloroform was unaffected by the hydrophilic PVP grafted because of good solubility of PVP polymer in halogenated hydrocarbon solvent. When the concentration of disperse phase was considered, its influence on resulting particles was obvious. Size of Janus particle decreased with a decrease in the concentration of disperse phase, but PSD increased (Fig. 3a–c, e–g and i–k and S1†). The effects of concentration on size and PSD depended on weight ratios of (PVP)PS and PMMA. For example, at 3 mg ml⁻¹, the size and PSD for weight ratio 3 : 1 PS/PMMA were better than for other two weight ratios (Fig. 3a, e and f and S1†), because at low concentration, the increase of PMMA content further disrupted the balance between oil phase and water phase in microfluidic channels. Therefore, the optimal concentration of oil phase was 10 mg ml⁻¹.

Fig. 3 The effects of concentrations and components of oil phases in microfluidics on the size and particle size distribution (PSD) of composite particles.

To obtain concaved PS particle, the dispersion media of the PS/PMMA Janus particles were changed from water to acetic acid to selectively dissolve the PMMA phases,³⁵ which could be explained based on solubility parameter δ. The difference between δ_PS and δ_CH3COOH is larger than that between δ_PMMA and δ_CH3COOH, because the values of δ(MPa^1/2) of PS, PMMA and acetic acid are 18.6, 19.4 and 20.7, respectively;³³ thus, acetic acid can dissolve PMMA instead of PS. When the surfaces of remained particles were smooth, the dissolution of PMMA compartment was finished. The thicknesses of concaved PS particles were also defined as the weight ratios of PS and PMMA in Janus particles. For PS/PMMA Janus particles, dissolution process was very fast and the surfaces of obtained concaved particles were smooth (see Fig. 4), but for (PVP)PS/PMMA Janus particles, this dissolution process took even longer.³⁵ The PVP stabilizer existed on the particle surface because of the separation of the PVP during the process of solvent evaporation.³⁴ Moreover, hydrogen bonds between the pyrrolidone groups of PVP stabilizer and carboxyl groups formed in the acidic hydrolysis process of PMMA;³⁴ hence, the final selection in experiments were PS and PMMA.

Fig. 4 Optical microscopy images (a–c) and corresponding SEM images (d–f) of concaved PS particles. These concaved PS particles were obtained by selectively dissolving PMMA domain in PS/PMMA Janus particles using acetic acid. In panels a–c, the insets are the enlarged views of concaved particles labelled with red dash circles.

Besides the concaved particles, our approach allows the preparation of other nonspherical particles; particle size is determined by the preparation parameters in microfluidics including flow rates and concentrations of disperse and continuous fluids, and particle shapes depend on polymer solutions as disperse fluids and solvents for selective dissolution.

Owing to unique shape anisotropy of concaved particle, depletion interactions were employed to induce the self-assembly of concaved particles, using PEO with a molecular weight of 600 000 as the depletant, unless stated otherwise. Depletion is a short-range attraction in dispersions of colloidal particles when a non-adsorbing water-soluble polymer, also termed depletant, was added to the system.^36,37 The center of mass of the depletant cannot approach colloid surface any closer than the radium of a depletant molecule (r_p); that is, a depletion zone exists next to the surface of each colloidal particle, restricting the volume available to the depletant coils.

When the separation of surfaces of two particles is less than diameter of the free depletant coil (2r_p), their depletion zones overlap and the total volume available to depletants increases by the amount of overlap volume (ΔV) between these two particles; therefore, the entropy of depletants increases, and an effective attraction arises between these two particles. When these two particles approach, the volume of total depletion zone decreases; hence, solvents and depletants are excluded from depletion zones toward bulk solutions, which lowers the free energy of this system and the free energy reduction (ΔF) is determined by overlap volume and number density of depletant as ΔF = −ρ_pk_BTΔV. Here, T is the temperature, and k_B is Boltzmann's constant. The negative corresponds to attractive depletion interaction, and the range of this interaction is given by diameter of depletant coil (2r_p). This attractive interaction was particularly strong in colloids with specific geometries such as buckled spheres and patchy particles with surface roughness.^4,5,14

However, van der Waals interaction between two microparticles follows a first power of distance and it is much reduced in a solvent medium, and moreover, the Coulomb force depends on the inverse-square distance and it is a long-range interaction. But hydrophobic interactions between concaved PS particles are considerable: concaved PS particles tend to hold together with random arrangement because of its strong hydrophobicity. To disperse concaved PS particles in ultrapure water, anionic surfactant (SDS) and nonionic surfactant, nonylphenoxypoly(ethyleneoxy)ethanol (NP40), were added to the system. SDS molecules are absorbed on the surface of concaved particle, which reduces the interfacial tension between polymer and an aqueous medium and produces a soft repulsive Coulomb potential competing with depletion attraction. While NP40 molecules sterically stabilize particles against irreversible aggregation and avoid adhesion of the particles to plastic containers.³⁸ All aqueous concaved particle dispersions discussed here contained 10 mM NaCl, which reduces the Debye length small enough for interacting particles to fully experience their nonspherical shape (10 mM monovalent salt with Debye length 3.0 nm).¹⁹ All aqueous concaved particle dispersions have an average zeta potential value (−38.98 mV at 3 mg ml⁻¹ SDS). In general, suspensions with zeta potential above 30 mV (absolute value) are physically stable. Fig. 5 illustrated the self assembled structures of concaved PS particles of different thickness, and concaved particles underwent depletion attraction competing with screened Coulomb potential when their surfaces come within of 2r_p each other.

Fig. 5 Optical microscopy images of final self-assembled structures, flexible worm-like chains, induced by depletion interaction, and polymers PEO served as the depletants. Red dash circles display typical polymeric chains. The samples for self-assemblies were mixtures of concaved particles dispersions, PEO aqueous solutions and NaCl solutions.

Clearly, the overlap of the depletion zones, and hence the depletion attraction, is maximized when the “lock” particle is occupied by the “key” particle whose radius matches that of the lock, namely, head-to-tail stacking. Here, the spherical part of the surface acts as key, and the cavity on each particle was labelled as lock. Representative self-assembled structures, polymeric worm-like chains with head-to-tail configuration, were shown in Fig. 5. Colloidal gels were formed in concentrated suspensions within 3 h by adding depletants, but for weight ratio 3 : 1 PS/PMMA particles, the formed colloidal gels was less stable (see Fig. 5c). Because the overlap volume of weight ratio 3 : 1 PS/PMMA particle is smaller than that of other two weight ratios ultimately leading to weaker depletion attraction. Moreover, when changing from 3D space (i.e., in the bulk) to 2D space (i.e., on a slide), for the particles with weaker depletion interactions, they were likely to redisperse in solutions resulting in the disaggregation of formed structures. To gain insight to the reversibility of this particle flocculation, the suspensions for self-assemblies were diluted with ultrapure water. Aggregates were disrupted and redispersed as small clusters and/or individual particles (Fig. 6a). Furthermore, to confirm whether the similar size nanoparticles could enhance the self-assembly process, cross-linked PS nanoparticles (nano-CPSs; Z-average diameter: 98.13 nm; polydispersity index: 0.042) were introduced into systems. The size of nano-CPS was similar to that of PEO polymer (the radium (r_p) of PEO used in experiments is ∼56 nm).⁵ Nano-CPSs depressed flocculation of concaved particles, no colloidal gels formed, and the binding between keys and locks became weakened (Fig. 6b). In Asakura and Oosawa model, depletants are regarded as hard, spherical particles,³⁹ and there exist two critical depletant concentrations in depletion flocculation.^40–42 Below the first one the flocculation would not exist, whereas above the second one, flocculation would not occur due to the appearance of higher energy barrier.⁴¹ When nano-CPSs were added, the depletant number densities in present experiment are 2 × 10¹² molecules per μl for PEO polymers and 2.3 × 10⁹ molecules per μl for nano-CPSs. It was close to the second critical concentration and there was an equilibrium distribution between flocculated and dispersed particles. In Fig. 6b, loose chains and dispersed particles coexisted and the loose chain was the thermodynamic metastable structure. The representative structures, worm-like chains, in Fig. 5 were previously described for “key-lock” colloids with self-complementary shapes both in computer simulations and experiments;^4,5,23 the morphology of the formed chain was a function of the sizes of particles and the interactions driving self-assembly processes.

Fig. 6 The reversibility of the self-assembly process of concaved particles, and the influence of nano-CPSs on the self-assembly of concaved particles. Panel (a) shown the results when a droplet of ultrapure water was added to the final observed sample on a slide and penal (b) displayed the self-assembled structures after a droplet of nano-CPSs emulsion was introduced the system. In this system, regular flocculation structures were already formed, and this system “reacted” for another one hour.

A striking and unique feature of our self-assemblies of concaved PS particles is that the sizes of concaved particles are much greater than reported researches. Because of the larger size, gravitational effect and hydrophobic attraction cannot be neglectable.^4,14 The gravitational height was estimated to be h = k_BT/F_g = k_BT/ΔρVg ≈ 9.3 nm, where Δρ is the density difference between the colloids and the surrounding fluids, g is the gravitational acceleration, V is the volume of a particle, k_B is the Boltzmann's constant and T is the temperature.⁴³ To prevent sedimentation, the microscope samples were rotated at a given speed. Moreover, hydrophobic attraction was adequately weakened by adding a combination of anionic surfactant (SDS) and nonionic surfactant (NP40) to the system.

Conclusions

In summary, our observations demonstrated the self-assemblies of large size concaved PS particles directed by depletion interactions, and these concaved particles preferred to stack on top of each other to form an ordered worm-like chains. The pair potential between concaved particles is a superposition of electrostatic repulsion, van der Waals attraction and depletion attraction. The approach we proposed in this work to prepare concaved particle is a hybrid of microfluids, solvent evaporation and selective dissolution, and the large size, uniform concaved PS particles were obtained by using acetic acid to selectively dissolve the PMMA phase of monodisperse Janus PS/PMMA composite particles which were the results of evaporation solvent, chloroform, from the droplets formed in microfluidic device with explicit flow rates and concentrations of disperse and continuous fluids.

Experimental section

Synthesis of PS and PMMA

PS and PMMA were synthesized by solution polymerization under the conditions listed in Table S1.†⁴⁴ After the polymerizations were finished, polymer solutions were slowly poured into excessive ethanol to precipitate PS (or PMMA).

Preparation of PS/PMMA janus particles

PS/PMMA emulsion droplets are formed in microfluidic device with a flow focusing geometry (Fig. 1). The water phase for microfluidic emulsification was sodium dodecyl sulfonate (SDS, 3 mg ml⁻¹) aqueous solution and the oil phase was polymer blends containing PS and PMMA, dissolved in chloroform with its concentration 10 mg ml⁻¹ and the weight ratios of PS and PMMA in polymer solutions were set to 3 : 1, 2 : 1 and 1 : 1, respectively. The above mentioned two phases were pumped into microfluidic device using syringe pumps (Lead Fluid TYD01 series) and the flow rates for oil phase and water phase were set at 8 μl min⁻¹ and 25 μl min⁻¹, respectively. The collected emulsion droplets were stored in uncovered glass vials for about 10 days to fully evaporate chloroform from the droplets. The microfluidics process was monitored using an inverted optical microscope (Jiangnan, XD 202, China) fitted with a camera (PixeLINK, PL-B742U, Canada).

Preparation concaved PS particles

The dispersions of PS/PMMA Janus Particles were centrifuged and then were redispersed in acetic acid to dissolve the PMMA phase because acetic acid dissolves PMMA but not PS. After completely dissolution, the remained particles were concaved PS particles.

Self-assembly of concaved PS particles

For depletion interaction, PEO polymers serving as depletants were dissolved in ultrapure water, and the microscope samples were prepared by mixing of aqueous solution of PEO polymers, colloidal dispersion and 10 mM NaCl. To avoid sedimentation the microscope samples were rotated (IKA, Vortex 4 digital) at a given speed (1000 rpm or 1300 rpm) according to the thickness of concaved particle.

Characterization

The production of emulsion droplets is observed with an inverted optical microscope (Jiangnan, XD 202, China) equipped with a high speed camera (PixeLINK, PL-B742U, Canada). For analysis of resultant composite particles, scanning electron microscope (Hitachi, S-4800, Japan) is used. The zeta potential of concaved PS particles is measured with a zeta potential analyzer (Brookhaven, ZetaPALS, USA).

Acknowledgements

The authors would like to thank the National Natural Science Foundation of China (no. 21474075, 91127046 and 21274107) and National Basic Research Program of China (973 Program, 2012CB821500) for funding this project. The authors thank Yu Chen, Professor of Tianjin University, China, for preparation of PS and PMMA.

Notes and references

1. L. Rossi, S. Sacanna, W. T. M. Irvine, P. M. Chaikin, D. J. Pine and A. P. Philipse, Soft Matter, 2011, 7, 4139.
2. J. W. Kim, R. J. Larsen and D. A. Weitz, Adv. Mater., 2007, 19, 2005.
3. C. I. Zoldesi, C. A. van Walree and A. Imhof, Langmuir, 2006, 22, 4343.
4. M. Marechal, R. J. Kortschot, A. F. Demirors, A. Imhof and M. Dijkstra, Nano Lett., 2010, 10, 1907.
5. S. Sacanna, W. T. Irvine, P. M. Chaikin and D. J. Pine, Nature, 2010, 464, 575.
6. S. Sacanna, W. T. Irvine, L. Rossi and D. J. Pine, Soft Matter, 2011, 7, 1631.
7. S. Sacanna, M. Korpics, K. Rodriguez, L. Colon-Melendez, S. H. Kim, D. J. Pine and G. R. Yi, Nat. Commun., 2013, 4, 1688.
8. S. H. Kim, A. D. Hollingsworth, S. Sacanna, S. J. Chang, G. Lee, D. J. Pine and G. R. Yi, J. Am. Chem. Soc., 2012, 134, 16115.
9. A. S. Utada, E. Lorenceau, D. R. Link, P. D. Kaplan, H. A. Stone and D. A. Weitz, Science, 2005, 308, 537.
10. A. Tao, P. Sinsermsuksakul and P. Yang, Angew. Chem., Int. Ed., 2006, 45, 4597.
11. J. Henzie, M. Grünwald, A. Widmer-Cooper, P. L. Geissler and P. Yang, Nat. Mater., 2012, 11, 131.
12. S. C. Glotzer and M. J. Solomon, Nat. Mater., 2007, 6, 557.
13. P. F. Damasceno, M. Engel and S. C. Glotzer, Science, 2012, 337, 453.
14. D. J. Kraft, R. Ni, F. Smallenburg, M. Hermes, K. Yoon, D. A. Weitz, A. van Blaaderen, J. Groenewold, M. Dijkstra and W. K. Kegel, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 10787.
15. S. Barua, J.-W. Yoo, P. Kolhar, A. Wakankar, Y. R. Gokarn and S. Mitragotri, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 3270.
16. S. Shen, T. Gu, D. Mao, X. Xiao, P. Yuan, M. Yu, L. Xia, Q. Ji, L. Meng, W. Song, C. Yu and G. Lu, Chem. Mater., 2012, 24, 230.
17. Y. Rao, Q. Tao, M. An, C. Rong, J. Dong, Y. Dai and W. Qian, Langmuir, 2011, 27, 13308.
18. Z. Cheng, F. Luo, Z. Zhang and Y.-q. Ma, Soft Matter, 2013, 9, 11392.
19. L. M. Ramirez, A. S. Smith, D. B. Unal, R. H. Colby and D. Velegol, Langmuir, 2012, 28, 4086.
20. L. M. Ramirez, C. A. Michaelis, J. E. Rosado, E. K. Pabon, R. H. Colby and D. Velegol, Langmuir, 2013, 29, 10340.
21. R. Ni, A. P. Gantapara, J. de Graaf, R. van Roij and M. Dijkstra, Soft Matter, 2012, 8, 8826.
22. M. Marechal and M. Dijkstra, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 031405.
23. D. J. Ashton, R. L. Jack and N. B. Wilding, Soft Matter, 2013, 9, 9661.
24. S. Xu, Z. Nie, M. Seo, P. Lewis, E. Kumacheva, H. A. Stone, P. Garstecki, D. B. Weibel, I. Gitlin and G. M. Whitesides, Angew. Chem., Int. Ed., 2005, 117, 734.
25. Z. Nie, W. Li, M. Seo, S. Xu and E. Kumacheva, J. Am. Chem. Soc., 2006, 128, 9408.
26. T. Nisisako, T. Torii, T. Takahashi and Y. Takizawa, Adv. Mater., 2006, 18, 1152.
27. R. K. Shah, J.-W. Kim and D. A. Weitz, Adv. Mater., 2009, 21, 1949.
28. N. Saito, Y. Kagari and M. Okubo, Langmuir, 2006, 22, 9397.
29. N. Saito, Y. Kagari and M. Okubo, Langmuir, 2007, 23, 5914.
30. M. Okubo, N. Saito and T. Fujibayashi, Colloid Polym. Sci., 2004, 283, 691.
31. Y. Xuan, J. Peng, L. Cui, H. Wang, B. Li and Y. Han, Macromolecules, 2004, 37, 7301.
32. N. G. Min, B. Kim, T. Y. Lee, D. Kim, D. C. Lee and S. H. Kim, Langmuir, 2015, 31, 937.
33. J. Brandrup, E. H. Immergut, E. A. Grulke, A. Abe and D. R. Bloch, Polymer handbook, Wiley, New York, 1999.
34. S. Onishi, M. Tokuda, T. Suzuki and H. Minami, Langmuir, 2015, 31, 674.
35. U. Akiva and S. Margel, J. Colloid Interface Sci., 2005, 288, 61.
36. S. Asakura and F. Oosawa, J. Chem. Phys., 1954, 22, 1255.
37. H. N. Lekkerkerker, W.-K. Poon, P. N. Pusey, A. Stroobants and P. Warren, Europhys. Lett., 1992, 20, 559.
38. S. Badaire, C. Cottin-Bizonne, J. W. Woody, A. Yang and A. D. Stroock, J. Am. Chem. Soc., 2007, 129, 40.
39. S. Asakura and F. Oosawa, J. Polym. Sci., 1958, 33, 183.
40. R. I. Feigin and D. H. Napper, J. Colloid Interface Sci., 1980, 74, 567.
41. R. I. Feigin and D. H. Napper, J. Colloid Interface Sci., 1980, 75, 525.
42. P. Jenkins and M. Snowden, Adv. Colloid Interface Sci., 1996, 68, 57.
43. V. Prasad, D. Semwogerere and E. R. Weeks, J. Phys.: Condens. Matter, 2007, 19, 113102.
44. Y. Wang, B.-H. Guo, X. Wan, J. Xu, X. Wang and Y.-P. Zhang, Polymer, 2009, 50, 3361.

---

Footnote

† Electronic supplementary information (ESI) available: Additional plots showing the corresponding size distribution of PS/PMMA and (PVP)PS/PMMA Janus particles were displayed in Fig. S1 and S2. See DOI: 10.1039/c5ra04110d

---