Mechanical properties and variation in SOC going from La to Nd in intermetallic RIn3 and RSn3 (R = La, Ce, Pr, Nd)
M. Shafiqab,
Iftikhar Ahmad*ab and
S. Jalali-Asadabadi*c
aCenter for Computational Materials Science, University of Malakand, Pakistan. E-mail: ahma5532@gmail.com; Tel: +92-332-906-7866
bDepartment of Physics, University of Malakand, Chakdara, Pakistan
cDepartment of Physics, Faculty of Science, University of Isfahan, Hezar Gerib Avenue, Isfahan 81746-73441, Iran. E-mail: saeid.jalali.asadabadi@gmail.com; sjalali@sci.ui.ac.ir; Tel: +98 9133287908
First published on 8th April 2015
Abstract
First principle studies of the cubic rare-earth intermetallics RIn3 and RSn3 (R = La, Ce, Pr, Nd) have been carried out within the framework of density functional theory using the full potential linearized augmented plane waves plus local orbital method (FP-LAPW + lo). The calculated structural parameters with different functionals are found to be consistent with the experimental results. The effect of the Hubbard potential on the density of states is discussed in detail. It is observed that the inclusion of spin–orbit coupling (SOC) causes degeneracies of the electronic band structures in the vicinity of the Fermi level of these compounds. Furthermore, the SOC effect enhances as one goes from La to Nd in a compound, which demonstrates the interesting nature of this effect in the periodic table. The elastic constants, bulk moduli, shear moduli, Young’s moduli, anisotropy, Kleinman parameters, Poisson’s ratios, sound velocities for shear and longitudinal waves, and Debye temperatures are calculated and discussed, which reveal that these compounds are ductile in nature.
I. Introduction
Rare-earth (RE) intermetallic compounds are strongly correlated electron systems, and in this family of compounds RX3 (R = rare-earth and X = In, Sn) are most exciting due to their interesting physics. The RX3 compounds have attracted both experimental and theoretical attention because of their diverse bulk properties, such as low superconducting transition temperature, magnetic susceptibility and thermoelectric power as a function of their electron concentration.1,2 These compounds offer many possibilities by replacing the X atom (X = In, Sn, Tl, Pb, etc.), and their single crystals can be easily grown due to their congruent melting.3 Many of the RX3 compounds crystallize in a cubic symmetry which is a more favorable structure for superconductivity than a lower symmetry.4 Furthermore, these compounds are stable in the cubic structure at standard temperature and pressure (STP) and remain stable over a wide range of pressures.5 In RSn3 solders (Sn-solder) the rare-earth elements La, Ce, Er and Eu are used which are suitable replacements for Pb–Sn solder.6 The amount of the RE element in Sn-solder improves both the physical and mechanical properties and in particular, enhances the ductility of the solder.7Due to unfilled 4f orbitals and spin–orbit interactions, the adjacent electronic states strongly interact with each other, therefore the characterization of accurate physical properties and the development of analytical and computational tools for lanthanide-based compounds is a challenging problem for both experimental and theoretical researchers.8 RX3 (R = La, Ce, Pr and Nd, X = In and Sn) intermetallic compounds crystallize in the cubic AuCu3-type crystal structure with space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (no. 221). The point groups of the R and X atoms are cubic m
m (no. 221). The point groups of the R and X atoms are cubic m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and non-cubic 4/mmm, respectively.9 In the RX3 compounds, the valency of the lanthanide can be inferred from lattice constant measurement techniques. The lattice constant of R2+ is larger than R3+ by almost 10% for pure lanthanides.10 For diluted lanthanides RX3 (R = Eu, Yb) (addition of other elements with the lanthanides), the lattice constant increases by less than 2% when compared to other RX3 compounds. This shows the unusual nature of Eu and Yb, which display divalency in this 4f series of compounds.9,11 Most of the RIn3 and RSn3 compounds are antiferromagnetic (AFM)12,13 except Pauli paramagnetic LaIn3, and paramagnetic LaSn3, CeSn3 and PrIn3.14–16 The AFM transition Néel temperatures (TN) for CeIn3, NdIn3, PrSn3 and NdSn3 are 10 K, 5.9 K, 8.6 K, and 4.7 K, respectively.17–19 Some RIn3 and RSn3 compounds exhibit superconductivity. The superconducting transition temperatures (TC) for LaIn3, LaSn3 and CeIn3 are 0.71 K, 6.5 K, and 0.2 K, respectively.20,21 Moreover, CeIn3 and PrSn3 are heavy fermion compounds.22,23 Due to both the localized and itinerant character of the f electrons, CeIn3 is also described as mixed valence or intermediate valence24 and CeSn3 is categorized as a Kondo compound with valence fluctuation.25 The Fermi surface properties and the de Haas–van Alphen (dHvA) effect in RX3 compounds were reported by Ōnuki and Settai,26 whereas the pressure dependent electronic structure and optical conductivity of the CeIn3 compound in the AFM phase were experimentally investigated by Iizuka et al.27
m and non-cubic 4/mmm, respectively.9 In the RX3 compounds, the valency of the lanthanide can be inferred from lattice constant measurement techniques. The lattice constant of R2+ is larger than R3+ by almost 10% for pure lanthanides.10 For diluted lanthanides RX3 (R = Eu, Yb) (addition of other elements with the lanthanides), the lattice constant increases by less than 2% when compared to other RX3 compounds. This shows the unusual nature of Eu and Yb, which display divalency in this 4f series of compounds.9,11 Most of the RIn3 and RSn3 compounds are antiferromagnetic (AFM)12,13 except Pauli paramagnetic LaIn3, and paramagnetic LaSn3, CeSn3 and PrIn3.14–16 The AFM transition Néel temperatures (TN) for CeIn3, NdIn3, PrSn3 and NdSn3 are 10 K, 5.9 K, 8.6 K, and 4.7 K, respectively.17–19 Some RIn3 and RSn3 compounds exhibit superconductivity. The superconducting transition temperatures (TC) for LaIn3, LaSn3 and CeIn3 are 0.71 K, 6.5 K, and 0.2 K, respectively.20,21 Moreover, CeIn3 and PrSn3 are heavy fermion compounds.22,23 Due to both the localized and itinerant character of the f electrons, CeIn3 is also described as mixed valence or intermediate valence24 and CeSn3 is categorized as a Kondo compound with valence fluctuation.25 The Fermi surface properties and the de Haas–van Alphen (dHvA) effect in RX3 compounds were reported by Ōnuki and Settai,26 whereas the pressure dependent electronic structure and optical conductivity of the CeIn3 compound in the AFM phase were experimentally investigated by Iizuka et al.27
Some theoretical studies on the pressure dependent structural, electronic and elastic properties of the intermetallic compounds LaIn3, LaSn3, CeIn3 and CeSn3 are available1,2,28,29 in the literature but their theoretical results are not consistent with the experiments because of the improper treatment of the exchange-correlation potential in those calculations. In these studies, they have used local density approximation (LDA) and generalized gradient approximation (GGA) where it is evident that RIn3 and RSn3 compounds are strongly correlated electron systems with 4f electrons. Therefore, to obtain the rational and logical electronic structures and other physical properties of these compounds, it is necessary to treat the strong correlation effects by an additional local Hubbard repulsion of magnitude U, i.e., DFT + U techniques as well as spin–orbit coupling (SOC) effects to increase the accuracy of the calculated results. These deliberations have been considered in carrying out the calculations of the structural, electronic, elastic and mechanical properties of the intermetallic compounds, RX3 (R = La, Ce, Pr and Nd, X = In and Sn). The calculations are carried out using the full potential linearized augmented plane waves plus local orbitals (FP-LAPW + lo) method under the framework of DFT. We have carried out these studies with the motivation that the elastic and mechanical properties of CeIn3, CeSn3, PrIn3, PrSn3, NdIn3 and NdSn3 have never been explored, neither theoretically nor experimentally, which may be promising materials with improved mechanical properties for practical applications. This study will cover the missing information in the literature about these materials and will also provide the basis for future experiments.
II. Method of calculations
The calculations have been performed by using density functional theory (DFT) implemented in the WIEN2k code30 and employing the full potential linearized augmented plane waves plus local orbitals (FP-LAPW + lo) method.31 The exchange-correlation effects are calculated within the local density approximation (LDA),32 generalized gradient approximation (GGA),33 GGAsol,34 Wu–Cohen GGA (WC-GGA),35 meta GGA (m-GGA)36 and hybrid functional B3PW91![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37,38 with spin polarization. As lanthanides are strongly correlated systems with localized 4f electrons,39,40 to obtain the exact nature of the electronic structure of the compounds under consideration, we used LDA + U and GGA + U methods. The DFT + U method is based on the Hubbard model, which treats the strongly correlated electron systems with an orbital dependent potential of Coulomb and exchange interactions.41 The optimized values of the U parameter are obtained by varying U, step by step. After examining several values for the U parameter, values were selected which gave better results for the magnetic moment in comparison with the experimental values for the corresponding compounds. The values of U used within the calculations are given in Table 1. One can clearly see a trend of increasing U with increasing atomic number. This is because with increasing atomic number, the f state becomes deeper and the orbitals become more localized, thus leading to an increased Coulomb interaction. Furthermore, spin–orbit coupling (SOC) is included to treat the relativistic effects. The SOC values are included using a second variational method.42 The second variational method, which makes use of the scalar-relativistic basis, is based on the reduction of the original basis. In the first step of this approach, the scalar-relativistic part of the Hamiltonian is diagonalized in the scalar-relativistic basis. In the second step, the full Hamiltonian matrix including SOC is constructed using the eigenfunctions of the first step Hamiltonian. Once the effects of the spin–orbit coupling are included, then the full Hamiltonian can be written as:
37,38 with spin polarization. As lanthanides are strongly correlated systems with localized 4f electrons,39,40 to obtain the exact nature of the electronic structure of the compounds under consideration, we used LDA + U and GGA + U methods. The DFT + U method is based on the Hubbard model, which treats the strongly correlated electron systems with an orbital dependent potential of Coulomb and exchange interactions.41 The optimized values of the U parameter are obtained by varying U, step by step. After examining several values for the U parameter, values were selected which gave better results for the magnetic moment in comparison with the experimental values for the corresponding compounds. The values of U used within the calculations are given in Table 1. One can clearly see a trend of increasing U with increasing atomic number. This is because with increasing atomic number, the f state becomes deeper and the orbitals become more localized, thus leading to an increased Coulomb interaction. Furthermore, spin–orbit coupling (SOC) is included to treat the relativistic effects. The SOC values are included using a second variational method.42 The second variational method, which makes use of the scalar-relativistic basis, is based on the reduction of the original basis. In the first step of this approach, the scalar-relativistic part of the Hamiltonian is diagonalized in the scalar-relativistic basis. In the second step, the full Hamiltonian matrix including SOC is constructed using the eigenfunctions of the first step Hamiltonian. Once the effects of the spin–orbit coupling are included, then the full Hamiltonian can be written as:
H![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) = ε = ε![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) + Hso + Hso![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif)
| (1) |
 | (2) |
![[small sigma, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c9.gif) represents the Pauli spin matrices.
represents the Pauli spin matrices.
| Comp. | LaIn3 | CeIn3 | PrIn3 | NdIn3 | LaSn3 | CeSn3 | PrSn3 | NdSn3 |
|---|---|---|---|---|---|---|---|---|
| U (eV) | 5.0 | 5.5 | 5.8 | 6.2 | 5.0 | 5.5 | 5.8 | 6.2 |
The radii of the muffin-tin spheres have been chosen as 2.50 au. for the rare-earth elements as well as for Sn and In. To achieve convergence, the basis set is expanded in terms of plane waves up to RMTKmax = 7 where RMT is the smallest atomic radius in a unit cell and Kmax is the magnitude of the maximum value of the k-vector in the plane waves expansion. For the valence wave function inside muffin-tin spheres, the maximum value of the angular momentum lmax = 10 is considered. In the interstitial region, the charge density is Fourier expanded up to Gmax = 12. High accuracy is required to calculate elastic properties, therefore by increasing the number of k-points, we tested the convergence of the total energy and hence the total energy is converged for 6000 k-points with a dense k mesh of 165 k-points in the irreducible wedge of the Brillouin zone with a grid size of 18 × 18 × 18 using the Monkhorst and Pack mesh.44
The elastic constants of RX3 are calculated with Cubic-elastic software,45 using the energy approach46 implemented in the WIEN2k code. In this work Voigt notations are replaced, which the number of elastic constants and hence for a cubic lattice only three independent elastic constants C11, C12 and C44 are left, which can be determined by introducing orthorhombic, cubic and monoclinic lattice distortions.47 These constants are calculated, and are further used to evaluate the mechanical properties of RX3 such as the shear modulus (G), Young’s modulus (Y), Cauchy pressure (C′′), Poisson’s ratio (ν), Kleinman parameter (ξ), and anisotropy constant (A) using standard relations.47,48
III. Results and discussion
A. Ground state structural properties
The ground state structural properties of RX3 (R = La, Ce, Pr and Nd, X = In and Sn) are calculated by finding the total energy of the unit cell for each compound with respect to volume using the Birch–Murnaghan equation of state.49 The lattice constant (a) and zero pressure bulk moduli (B0) are determined using a variety of schemes including LDA, GGA, GGAsol, WC-GGA, LDA + U, GGA + U, and meta-GGA (m-GGA), as well as B3PW91 hybrid functionals.The theoretically calculated results of the lattice constants and bulk moduli along with the available experimental data are listed in Tables 2 and 3, respectively.
| Comp. | LDA | GGAsol | GGA | WC | LDA + U | GGA + U | B3PW91 | m-GGA | Exp. |
|---|---|---|---|---|---|---|---|---|---|
| a Ref. 13.b Ref. 66. | |||||||||
| LaIn3 | 4.645 | 4.697 | 4.787 | 4.704 | 4.698 | 4.835 | 4.738 | 4.789 | 4.732a |
| CeIn3 | 4.554 | 4.601 | 4.718 | 4.609 | 4.612 | 4.761 | 4.676 | 4.708 | 4.687a |
| PrIn3 | 4.546 | 4.605 | 4.705 | 4.617 | 4.647 | 4.795 | 4.669 | 4.701 | 4.670a |
| NdIn3 | 4.540 | 4.603 | 4.689 | 4.609 | 4.626 | 4.765 | 4.647 | 4.696 | 4.653a |
| LaSn3 | 4.686 | 4.728 | 4.816 | 4.736 | 4.738 | 4.864 | 4.773 | 4.815 | 4.769b |
| CeSn3 | 4.589 | 4.626 | 4.755 | 4.637 | 4.636 | 4.785 | 4.710 | 4.749 | 4.721b |
| PrSn3 | 4.582 | 4.632 | 4.729 | 4.647 | 4.661 | 4.839 | 4.709 | 4.734 | 4.716b |
| NdSn3 | 4.581 | 4.624 | 4.713 | 4.637 | 4.644 | 4.776 | 4.701 | 4.713 | 4.705b |
| Comp. | LDA | GGAsol | GGA | WC | LDA + U | GGA + U | B3PW91 | m-GGA |
|---|---|---|---|---|---|---|---|---|
| LaIn3 | 60.816 | 58.184 | 52.293 | 58.653 | 60.188 | 53.720 | 56.213 | 52.157 |
| CeIn3 | 74.382 | 63.580 | 52.703 | 63.166 | 61.029 | 51.628 | 61.100 | 50.536 |
| PrIn3 | 63.110 | 61.015 | 53.319 | 61.106 | 54.015 | 59.587 | 53.044 | 54.791 |
| NdIn3 | 63.493 | 61.943 | 52.527 | 59.278 | 69.926 | 49.240 | 64.591 | 49.120 |
| LaSn3 | 65.837 | 60.339 | 53.861 | 59.064 | 61.507 | 56.910 | 55.646 | 50.004 |
| CeSn3 | 79.210 | 71.621 | 67.212 | 71.920 | 71.445 | 55.026 | 70.686 | 60.948 |
| PrSn3 | 70.565 | 66.817 | 52.580 | 64.541 | 67.438 | 52.322 | 55.720 | 49.704 |
| NdSn3 | 72.514 | 62.381 | 56.295 | 66.712 | 69.969 | 51.222 | 52.950 | 51.046 |
The calculated GGA, GGA + U and m-GGA lattice constants are slightly larger than those of GGAsol, WC-GGA, LDA + U and B3PW91, while the calculated values for the bulk moduli by GGA, GGA + U and m-GGA for these compounds are smaller than those of the GGAsol and WC-GGA and B3PW91. This confirms the general trend of these approximations, that GGA overestimates and LDA underestimates lattice constants.34 Table 2 indicates that the computed lattice constants using the B3PW91 hybrid functional are in better agreement with the experimental values than the other theoretical approaches. It is also clear from the table that B3PW91 is the best performing functional for strongly correlated systems as compared to the other schemes. Table 2 also shows that as we move from La to Nd, the lattice constants are contracted, which can be attributed to the lanthanide contraction, i.e., the decrease in the atomic radius along the lanthanide series from left to right due to the poor shielding effect of the 4f electrons. Table 3 shows that the calculated bulk moduli using B3PW91 for all of the compounds are very close to each other and lie in the range of 52.950 and 70.686 GPa. This trend of the bulk moduli is also evident from the calculated results using GGAsol, GGA, m-GGA WC-GGA and LDA + U. No experimental data to the best of our knowledge is available for the bulk moduli, so our results are considered as a prediction for these properties of RIn3 and RSn3 (R = La, Ce, Pr and Nd) compounds.
B. Electronic structure and density of states
In order to reveal the electronic band structure, the spin polarized total density of states (TDOS) and 4f density of states are calculated by employing GGA and LDA for the exchange and correlation functional. The DOSs calculated by GGA and LDA approximations are quite similar and only the GGA density of states and 4f-DOSs for RIn3 and RSn3 (R = La, Ce, Pr and Nd, X = In and Sn) are presented in Fig. 1, where the Fermi level is set at 0 eV. It is clear from the figure that no band gap is available at the Fermi level for any of the intermetallic compounds under consideration; hence all of these compounds are metallic in nature. The figure also reveals the dominating character of the f state in all of these compounds. It is also evident from the figure that no prominent peak occurs at the Fermi level for any of these compounds under study; therefore all of these compounds are ductile in nature. The maximum peaks of LaIn3 and LaSn3 are above the Fermi level in the unoccupied states around 2.74 eV and 2.95 eV, respectively. Therefore, the LaIn3 and LaSn3 compounds show more ductility than the remaining RIn3 and RSn3 compounds, which is due to the large separation between the Fermi level and the f states according to a previous study.50 | ||
| Fig. 1 Total density of states TDOSs (red shading) and partial 4f-DOSs (blue shading) of RIn3 and RSn3 for R = La, Ce, Pr and Nd calculated with GGA. | ||
Strongly correlated systems such as lanthanides (and actinides)39,51 which involve 4f (or 5f) orbitals have interesting physical and chemical properties, because these electrons can be localized or itinerant depending on the crystalline environment. Therefore, to understand the effects of the 4f orbitals in these compounds, the calculations are also carried out with the Hubbard potential U (GGA + U and LDA + U). The total density of states (TDOSs) with GGA + U and partial density of states (DOSs) of the f states, as well as the TDOS with GGA, are plotted in Fig. 2. It is clear from the figure that both GGA and GGA + U provide different DOSs. The differences in the DOSs for all of the compounds can be clearly seen from the figure. The figure clearly indicates that the strong peaks which are due to the 4f states are significantly shifted up and down by the application of the Hubbard potential (U) as compared to the GGA scheme. This is in agreement with previous DFT calculations which show the Hubbard potential opens the gap between the occupied and unoccupied states.52
 | ||
| Fig. 2 Total density of states (TDOSs) with GGA (red lines), GGA + U (green shading) and PDOSs GGA + U-4f of RIn3 and RSn3 for R = La, Ce, Pr and Nd. | ||
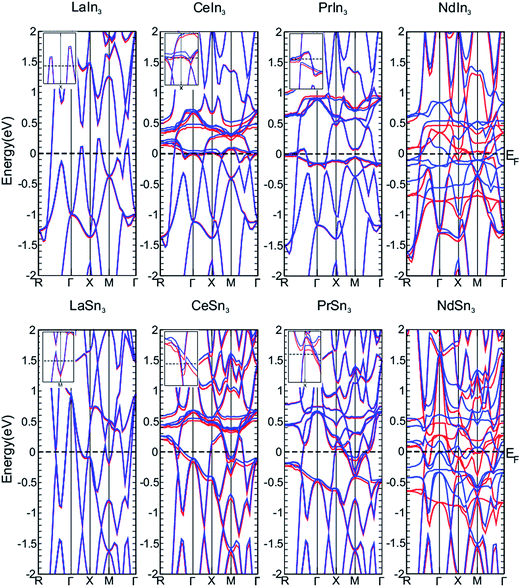
Spin–orbit coupling (SOC), which was apparently a weak relativistic correction to the Schrödinger equation in condensed matter physics, has recently attracted enormous attention in modern condensed-matter physics because of its key role in 5d, 4f and 5f electronic states. The spin and orbital degrees of freedom are entangled at a local level by the SOC, where the total angular momentum provides a good description of the ordered phases and fluctuation properties of a material and can also describe the possible uses of a material in various devices with prominent functionalities.53 To see the effect of the spin–orbit coupling (SOC) in the compounds under study their band structures along high symmetry directions with GGA and GGA + SOC are presented in Fig. 3. It is clear from the figure that the effect on the band structures of LaIn3 and LaSn3 is very small, which is in agreement with earlier work.1,54 The comparison of the band structures of these compounds reveals that, as one moves from La to Nd, the effect of SOC increases. This might be due to the fact that as the Coulomb attraction on an electron in a particular orbit increases, from La to Nd in the periodic table, the orbit shrinks and hence the electron speeds up to conserve the momentum of the system, where with this increase in the speed the relativistic effects of SOC increase. The differences between the GGA and GGA + SOC band structures in the vicinity of the Fermi level are shown in the insets of each compound in Fig. 3 lifting some degeneracies in the band structures. The figure also shows that the band along the symmetry line between X and M in the CeIn3 compound, dips below the Fermi level in the GGA scheme but stays above the Fermi level when SOC is introduced. The degeneracy in PrIn3 is observed at the R symmetry line, whereas in CeSn3 and PrSn3, the degeneracies occur at the M symmetry line. The SOC effects can be clearly seen for different symmetry lines in NdIn3 and NdSn3.
C. Elastic and mechanical properties
The elastic constants of solids provide significant information about the nature of the forces operating in solids. Elastic constants are very important for understanding the relationship between the crystal structure and bonding nature. These constants also reveal the structural stability and various other important physical properties of materials. The elastic constants C11, C12, and C44 for RIn3 and RSn3 (R = La, Ce, Pr and Nd) are calculated within GGA and GGAsol with spin polarization and are given in Table 4. The available experimental elastic constants (for LaSn3) along with other theoretical results are also listed in the table. No experimental data is available for these compounds except LaSn3. It is clear from the table that our calculated values for the elastic constants of the LaSn3 compound with GGAsol are in excellent agreement with the experimental results of Stassis et al.,55 extracted from the phonon dispersion curves, as compared to other theoretical results reported in ref. 1 and 28. Hence, from the consistency of our calculated values with the experimental results for this compound, we infer that our calculated values for the remaining compounds under investigation will also be consistent with the corresponding experimental values. Moreover, the stability criteria initiated by Born56 for cubic systems in terms of elastic constants, i.e., C11 − C12 > 0, C44 > and C11 + 2C12 > 0 are well satisfied by these compounds. The fulfillment of these criteria justifies that these intermetallic compounds are elastically stable.| Comp. | EXC | LaIn3 | CeIn3 | PrIn3 | NdIn3 | LaSn3 | CeSn3 | PrSn3 | NdSn3 |
|---|---|---|---|---|---|---|---|---|---|
| a Ref. 55.b Ref. 1.c Ref. 28. | |||||||||
| C11 | GGAsol | 89.265 | 95.500 | 83.878 | 82.569 | 69.273 | 99.084 | 80.343 | 87.167 |
| GGA | 97.525 | 100.909 | 80.152 | 85.405 | 86.732 | 85.005 | 80.247 | 96.191 | |
| Exp. | 70.50a | ||||||||
| Other | 97.30b, 83.17c | ||||||||
| C12 | GGAsol | 42.555 | 45.609 | 37.137 | 41.498 | 42.328 | 53.678 | 38.842 | 34.211 |
| GGA | 50.885 | 49.383 | 29.183 | 60.287 | 43.855 | 57.967 | 44.094 | 25.357 | |
| Exp. | 42.00a | ||||||||
| Other | 53.6b, 45.51c | ||||||||
| C44 | GGAsol | 27.280 | 29.879 | 32.365 | 35.340 | 27.584 | 48.904 | 28.575 | 30.375 |
| GGA | 28.125 | 37.543 | 34.767 | 33.997 | 35.463 | 45.431 | 28.370 | 27.367 | |
| Exp. | 33.50a | ||||||||
| Other | 44.20b, 31.22c | ||||||||
The trend of the mechanical properties of a material could be estimated from its elastic constants. As the elastic constants C11, C12, and C44, calculated by both GGA and GGAsol, exchange and correlation effects are very close to each other, therefore in this article the mechanical properties of the compounds are evaluated using the GGAsol results. The main mechanical parameters, i.e. shear modulus (G), Young’s modulus (Y), Pugh’s ratio (B/G), Cauchy’s pressure (C′′), Poisson’s ratio (ν) and anisotropic ratio (A), which are important for industrial applications are calculated and presented in Table 5. These important parameters are used to characterize the mechanical behavior of a material.
| Comp. | LaIn3 | CeIn3 | PrIn3 | NdIn3 | LaSn3 | CeSn3 | PrSn3 | NdSn3 |
|---|---|---|---|---|---|---|---|---|
| GV | 25.710 | 27.906 | 28.767 | 29.418 | 22.139 | 38.424 | 25.445 | 28.816 |
| GR | 25.562 | 27.689 | 28.047 | 27.430 | 19.849 | 33.459 | 24.830 | 28.686 |
| GH | 25.636 | 27.797 | 28.407 | 28.424 | 20.994 | 35.941 | 25.138 | 28.916 |
| Y | 67.219 | 72.832 | 73.020 | 74.939 | 57.971 | 97.183 | 65.749 | 72.940 |
| B/G | 2.267 | 2.239 | 1.856 | 1.942 | 2.412 | 1.915 | 2.095 | 1.794 |
| C′′ | 15.275 | 15.730 | 4.772 | 6.158 | 13.744 | 4.774 | 10.267 | 3.836 |
| v | 0.307 | 0.305 | 0.269 | 0.274 | 0.309 | 0.265 | 0.292 | 0.266 |
| ζ | 0.796 | 0.797 | 0.743 | 0.838 | 0.994 | 0.902 | 0.807 | 0.666 |
| A | 1.168 | 1.198 | 1.385 | 1.721 | 1.974 | 2.154 | 1.377 | 1.147 |
| C′ | 23.355 | 24.946 | 23.371 | 20.536 | 13.973 | 22.703 | 20.751 | 26.478 |
The average Hill’s57 shear modulus, GH = G, as a measure of resistance to plastic deformation upon shear stress is the arithmetic mean of the Reuss and Voigt shear moduli.58,59 The values of GH given in Table 5 indicate that CeSn3 offers more resistance to plastic deformation than the remaining compounds. The Young’s modulus (Y) defines the ratio between the linear stress and strain. The larger the value of Y, the stiffer the material will be. From Table 5 one can see that CeSn3 has the largest Young’s modulus value (stiffer). The higher values for the Young’s moduli as compared to their bulk moduli confirm the stiffness of these compounds. The Hill’s and shear moduli are further used to explain the ductile and brittle nature of a compound.
Pugh60 suggested an index for the ductility and brittleness of a material. The Pugh’s ratio (B/G) reflects the competition between the shear and cohesive strength of a material and describes its ductile/brittle character. If B/G is greater than the critical value 1.75, the material behaves in a ductile manner; otherwise the material will be brittle in nature. It is evident from Table 5, that the B/G ratio for all of the RIn3 and RSn3 compounds show a ductile behavior (B/G > 1.75). The larger values of B/G for LaSn3 (2.412) and for LaIn3 (2.267) reveal a higher degree of ductility. The same nature has also been observed in the DOSs plot (Fig. 1) for LaSn3 and LaIn3, showing that they have a more ductile nature than the other compounds. The ductile and brittle behavior of a compound can be also discussed in terms of the elastic constants C12 and C44. The Cauchy’s pressure (C′′ = C12 − C44) is used for this purpose and its positive/negative value shows the ductile/brittle behavior of a compound. The positive value of Cauchy’s pressure (from Table 5) indicates that all of the compounds under investigation are ductile in nature, which confirms the results of the Pugh’s B/G ratio. Cauchy’s pressure is also used to indicate the bonding character of the compounds. The positive value of Cauchy’s pressure is responsible for ionic bonding, while a material with negative Cauchy’s pressure requires angular or directional character in bonding (covalent bonding). It is clear from Table 5 that all of the compounds possess positive Cauchy’s pressure values, have metallic bonds and hence high mobility characteristics.
The Poisson’s ratio ν usually quantifies the stability of a crystal against shear (compressibility). Its typical lower and upper bound limits are −1 and 0.5 respectively. The lower limit bound is where the material does not change its shape and the upper limit bound is where the volume remains unchanged.61 Our calculated values for the Poisson’s ratio lie between 0.313 and 0.265, which show that these materials are less compressible and stable against external deformation. The Poisson’s ratio also demonstrates the ductile/brittle nature of a material. For ductile compounds ν ≈ 0.3 and for brittle ν > 0.35. The Poisson’s ratio for all of these compounds is less than 0.35, which further confirms the ductile nature of these compounds. Furthermore, the Poisson’s ratio also gives information about bonding forces. For central forces in solids, the lower limit of ν is 0.25 and the upper limit of ν is 0.5.62 The table shows that the calculated values of the Poisson’s ratio fall within this limit and that the dominant interatomic forces are central forces.
The Kleinman internal strain parameter (ζ) describes the relative tendency of bond bending versus bond stretching.63 Minimizing bond bending leads to ζ = 0, while minimizing bond stretching leads to ζ = 1. The calculated Kleinman parameters in Table 5 predict that in RIn3 and RSn3 compounds bond stretching is dominant (upper limit of ζ).
The anisotropic ratio (A) which measures the elastic anisotropy of a material is a very important property and is closely related to the induced microcracks in a material.64 For an ideal isotropic material, the anisotropic ratio is unity and deviation from unity measures the amount of anisotropy. From Table 5 one can see that the value of the anisotropic ratio is found to be much greater than 1. The deviations from unity specify that these compounds are not elastically isotropic and their properties vary strongly in different directions.
The important parameter, which defines the dynamical stability of a material, is the shear constant C′. It is also one of the criterions of mechanical stability and shows the stability of the tetragonal distortion. Its values for the compounds under consideration are given in Table 5. The positive values of the shear constant (C′ > 0) fulfill the required criteria for dynamical stability. From the calculated value of C′ it is predicted that these compounds are dynamically stable materials.
D. Sound velocities and Debye temperatures
The thermo-physical properties like longitudinal vl, transverse vs, average sound velocities vm, and Debye temperatures θ(D) of the compounds under study are also investigated. The Debye temperature θ(D) of a compound can be calculated using the following relationship:65
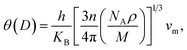 | (3) |
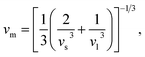 | (4) |
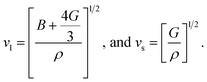 | (5) |
The calculated theoretical densities, sound velocities and Debye temperatures are reported in Table 6. The calculated densities are in excellent agreement with the available experimental values in parentheses. A material with a greater Debye temperature will be stiffer and exhibit high thermal conductivity. Table 6 shows that CeSn3 is stiffer than the other compounds (θ(D) = 151.05), which confirms the result of the Young’s modulus for CeSn3 (Y = 97.183). The lower Debye temperature of LaSn3 is a consequence of the lower elastic constant compared to the values of the rest of the compounds.
| Comp. | ρ | vl | vs | vm | θ(D) |
|---|---|---|---|---|---|
| a Ref. 3. | |||||
| LaIn3 | 7.316 (7.45a) | 3551.97 | 1871.88 | 2092.91 | 130.18 |
| CeIn3 | 7.661 | 3600.34 | 1904.86 | 2166.58 | 136.73 |
| PrIn3 | 7.737 | 3421.79 | 1916.10 | 2132.72 | 134.78 |
| NdIn3 | 7.871 | 3439.08 | 1900.38 | 2117.45 | 134.46 |
| LaSn3 | 7.358 (7.46a) | 3269.06 | 1689.14 | 1891.06 | 116.92 |
| CeSn3 | 7.664 | 3902.84 | 2165.59 | 2412.16 | 151.05 |
| PrSn3 | 7.804 | 3323.42 | 1794.79 | 2003.25 | 126.14 |
| NdSn3 | 7.936 | 3375.35 | 1908.81 | 2122.88 | 134.12 |
IV. Conclusions
In summary, we have performed theoretical analyses of the structural, electronic and elastic properties of RIn3 and RSn3 (R = La, Ce, Pr and Nd) using density functional theory. The calculated structural properties of the compounds are consistent with experimental results. The density of states and band structures reveal the intermetallic nature of these compounds. It is concluded that the spin–orbit coupling effect, which is a correction to the Schrödinger wave equation, enhances as one goes from La to Nd in a compound, which demonstrates the interesting nature of this effect in the periodic table. We discussed the influence of the spin–orbit coupling strength on the band structure. Mechanical properties were also evaluated using elastic constants. From the calculated elastic properties and other mechanical properties, all of the compounds investigated are found to be ductile in nature with elastic anisotropy.References
- S. Ram, V. Kanchana, G. Vaitheeswaran, A. Svane, S. B. Dugdale and N. E. Christensen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 174531 CrossRef.
- S. Ram, V. Kanchana, A. Svane, S. B. Dugdale and N. E. Christensen, J. Phys.: Condens. Matter, 2013, 25, 155501 CrossRef PubMed.
- R. J. Gambmo, N. R. Stemple and A. M. Toxen, J. Phys. Chem. Solids, 1968, 29, 295 CrossRef.
- I. R. Harris and G. V. Raynor, J. Less-Common Met., 1965, 9, 7 CrossRef CAS.
- N. V. C. Shekar and P. C. Sahu, J. Mater. Sci., 2006, 41, 3207 CrossRef CAS PubMed.
- C. F. Li, Z. Q. Liu, P. J. Shang and J. K. Shang, Scr. Mater., 2011, 65, 1049 CrossRef CAS PubMed.
- M. A. Dudek and N. Chawla, Intermetallics, 2010, 18, 1016 CrossRef CAS PubMed.
- I. N. Yakovkin, T. Komesu and P. A. Dowben, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 035406 CrossRef.
- S. J. Asadabadi, S. Cottenier, H. Akbarzadeh, R. Saki and M. Rots, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 195103 CrossRef.
- K. A. Gschneider Jr, Solid State Phys., 1964, 16, 275 Search PubMed.
- S. Jalali Asadabadi and H. Akbarzadeh, Phys. B, 2004, 349, 76 CrossRef PubMed.
- Z. Kletowski, Solid State Commun., 1989, 72, 901 CrossRef CAS.
- K. H. J. Buschow, H. W. de Wijn and A. M. van Diephen, J. Chem. Phys., 1969, 50, 137 CrossRef CAS PubMed.
- I. Umehara, N. Nagai and Y. Ōnuki, J. Phys. Soc. Jpn., 1991, 60, 1294 CrossRef CAS.
- I. Umehara, Y. Kurosawa, N. Nagai, M. Kikuchi, K. Satoh and Y. Ōnuki, J. Phys. Soc. Jpn., 1990, 59, 2848 CrossRef CAS.
- Y. Ōnuki and R. Settai, Low Temp. Phys., 2012, 38, 119 CrossRef PubMed.
- N. D. Mathur, F. M. Grosche, S. R. Julian, I. R. Walker, D. M. Freye, R. K. W. Haselwimmer and G. G. Lonzarich, Nature, 1998, 394, 39 CrossRef CAS PubMed.
- Z. Kletowski, Solid State Commun., 1987, 62, 745 CrossRef CAS.
- K. Kawashima, M. Maruyama, M. Fukuma and J. Akimitsu, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094517 CrossRef.
- A. Freeman and D. Koelling, J. Phys., 1972, 33, C3–C57 Search PubMed.
- S. D. Johnson, J. R. Young, R. J. Zieve and J. C. Cooley, Solid State Commun., 2012, 152, 513 CrossRef CAS PubMed.
- W. R. Johanson, G. W. Crabtree, A. S. Edelstein and O. D. MacMasters, Phys. Rev. Lett., 1981, 45, 504 CrossRef.
- R. Settai, K. Sugiyama, A. Yamaguchi, S. Araki, K. Miyake, T. Takeuchi, K. Kindo, Y. Ōnuki and Z. Kletowski, J. Phys. Soc. Jpn., 2000, 69, 3983 CrossRef CAS.
- K. A. Gschneider Jr, S. K. Dhar, R. J. Stierman, T. W. E. Tsang and O. D. MacMasters, J. Magn. Magn. Mater., 1985, 47 & 48, 51 Search PubMed.
- A. P. Murani, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 2308 CrossRef CAS.
- Y. Ōnuki and R. Settai, Low Temp. Phys., 2012, 38, 89 CrossRef PubMed.
- T. Iizuka, T. Mizuno, B. Hun Min, Y. S. Kwon and S. ichi Kimura, J. Phys. Soc. Jpn., 2012, 81, 043703 CrossRef.
- J. A. Abraham, G. Pagare, S. S. Chouhan and S. P. Sanyal, Comput. Mater. Sci., 2014, 81, 423 CrossRef CAS PubMed.
- J. A. Abraham, G. Pagare, S. S. Chouhan and S. P. Sanyal, Intermetallics, 2014, 51, 1 CrossRef CAS PubMed.
- P. Blaha, K. Schwarz, G. k. H. Madsen, D. Kuasnicka and J. Luitz, WIEN2K, an augmented plane wave + local orbitals program for calculating crystal properties, K. Schwarz, Technical Universitat, Wien, Austria, 2001 Search PubMed.
- O. K. Andersen, Phys. Rev. B: Solid State, 1975, 12, 3060 CrossRef CAS.
- J. P. Perdew and A. Zuanger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhop, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- J. P. Perdrew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef.
- Z. Wu and R. E. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 235116 CrossRef.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS PubMed.
- J. P. Perdew, S. Kurth, A. Zupan and P. Blaha, Phys. Rev. Lett., 1999, 82, 2544 CrossRef CAS.
- Z. Ali, B. Khan, I. Ahmad, I. Khan and S. Jalali Asadabadi, J. Magn. Magn. Mater., 2015, 381, 34 CrossRef CAS PubMed.
- S. Jalali Asadabadi, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 205130 CrossRef.
- S. Jalali Asadabadi and F. Kheradmand, J. Appl. Phys., 2010, 108, 073531 CrossRef PubMed.
- V. I. Anisimov, I. V. Solovyev, M. A. Korotin, M. T. Czyzyk and G. A. Sawatzky, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 16929 CrossRef CAS.
- D. D. Koelling and B. N. Harmon, J. Phys. C: Solid State Phys., 1977, 10, 3107 CrossRef CAS.
- P. Novák, Calculation of spin-orbit coupling, 1997, http://www.wien2k.a/reg_user/textbooks/novak_lecture_on_spinorbit.ps.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- M. Jamal, S. J. Asadabadi, I. Ahmad and H. A. R. Aliabad, Comput. Mater. Sci., 2014, 95, 592 CrossRef CAS PubMed.
- R. Stadler, W. Wolf, R. Podloucky, G. Kresse, J. Furthmuller and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1729 CrossRef CAS.
- M. Shafiq, S. Arif, I. Ahmad, S. Jalali Asadabadi, M. Maqbool and H. A. R. Aliabad, J. Alloys Compd., 2015, 618, 292 CrossRef CAS PubMed.
- M. Shafiq, I. Ahmad and S. J. Asadabadi, J. Appl. Phys., 2014, 116, 103905 CrossRef PubMed.
- F. Birch, Phys. Rev., 1947, 71, 809 CrossRef CAS.
- K. A. Gschneidner Jr, M. Ji, C. Z. Wang, K. M. Hoa, A. M. Russell, Ya. Mudryk, A. T. Becker and J. L. Larson, Acta Mater., 2009, 57, 5876 CrossRef PubMed.
- M. Zarshenas and S. J. Asadabadi, Thin Solid Films, 2012, 520, 2901 CrossRef CAS PubMed.
- K. Tao, J. Zhou, Q. Sun, Q. Wang, V. S. Stepanyuk and P. Jena, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 085103 CrossRef.
- H. Onishi, J. Phys.: Conf. Ser., 2012, 391, 012102 CrossRef.
- S. B. Dugdale, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 012502 CrossRef.
- C. Stassis, J. Zarestky, C. K. Loong, O. D. McMasters and R. M. Nicklow, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 2227 CrossRef CAS.
- M. Born and K. Huang, Dynamical Theory of Crystal Lattices, Clarendon, Oxford, 1954 Search PubMed.
- R. Hill, Proc. Phys. Soc., London, 1952, 65, 350 Search PubMed.
- A. Reuss, Z. Angew. Math. Mech., 1929, 9, 49 CrossRef CAS PubMed.
- W. Voigt, Lehrburch der Kristallphysik, Teubner, Leipzig, 1928 Search PubMed.
- S. F. Pugh, Philos. Mag., 1954, 45, 823 CrossRef CAS.
- V. Kanchana, Europhys. Lett., 2009, 87, 26006 CrossRef.
- H. Fu, D. Li, F. Peng, T. Gao and X. Cheng, Comput. Mater. Sci., 2008, 44, 774 CrossRef CAS PubMed.
- L. Kleinman, Phys. Rev., 1962, 128, 2614 CrossRef CAS.
- V. Tvergaard and J. W. Hutchinson, J. Am. Ceram. Soc., 1988, 71, 157 CrossRef CAS PubMed.
- L. Fast, J. M. Wills, B. Johansson and O. Eriksson, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 17431 CrossRef CAS.
- J. P. Sanchez, J. M. Friedt, G. K. Shenoy, A. Percheron and J. C. Achard, J. Phys. C: Solid State Phys., 1976, 9, 2207 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2015 |