Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A method distinguishing between guest molecules that can form sI, sII, and sH hydrogen clathrates
Alexander A.
Atamas
*a,
Simon W.
de Leeuw
b and
Herma M.
Cuppen
a
aInstitute for Molecules and Materials, Radboud University, Heyendaalseweg 135, 6525 AJ Nijmegen, The Netherlands. E-mail: a.atamas@science.ru.nl
bLeiden Institute of Chemistry, Gorlaeus Laboratories, Leiden University, P.O. Box 9502, 2300 RA Leiden, The Netherlands
First published on 10th March 2015
Abstract
A new method based on free energy calculations is proposed for discriminating between promoters that can form sI, sII, and sH hydrogen clathrates. The method is validated by comparing results of this computational approach to known experimental data reporting which type of clathrate structure is formed with the help of a particular promoter molecule. Good agreement is found. The free energy results confirm a well-known simple rule of thumb based on the van der Waals volume of the promoter molecules to distinguish between potential sH or sII hydrate formers. The method predicts an unusually strong temperature dependence of the stability of hydrogen clathrate hydrates for some hitherto untested promoter molecules, which can be exploited if easy release of hydrogen is required.
I. Introduction
Clathrate hydrates are molecular crystals consisting of a hydrogen-bonded water framework with enclathrated guest molecules1 stabilizing the compounds. Clathrates have been proposed as potential systems for hydrogen storage, because they can hold gas at relatively high density in molecular form. However, extreme pressures of ∼220 MPa are required for the formation of stable pure hydrogen clathrates,2,3 but the formation pressure can be significantly reduced by putting a second guest molecule, a so-called promoter, in the large cavities of hydrogen clathrate hydrates.4 There are three important structures of gas hydrates: cubic structure I (sI) with two small and six large cages, cubic structure II (sII) with sixteen small and eight large cages, and hexagonal structure H (sH) with three small, two medium and one large cavity in the unit cell. The latter structure is particular promising for hydrogen storage since it allows the highest density storage when both the small and medium cages are occupied by H2. The aim of this work is to present and validate a predictive screening method for discriminating between promoters that form hydrogen sI, sII, and sH clathrates. Since the most prospective candidates for hydrogen storage material are structures II and H, in this study we focus mainly on sII and sH hydrogen clathrate hydrates.Many organic water-soluble and -insoluble compounds have been identified experimentally as efficient stabilizing promoter molecules for sI, sII, and sH hydrogen clathrate formation. Frankcombe et al.5 presented a computational method to discriminate between guest molecules that form sII clathrate and molecules capable (together with a help gas) to form sH clathrate hydrate. The screening method is based on calculations of the difference between the energies of sII and sH clathrate formation. A clathrate formation energy is defined with reference to the total potential energies of the corresponding clathrate structure (sII or sH) and of the potential energy of hexagonal ice structure. The clathrate formation energy defined by Frankcombe et al. requires knowledge of the empty clathrate energy. The expressions of the energy of sII clathrate formation and the formation energy for sH clathrate formation consider only configurational, i.e., potential energy. Hence, the considerations are valid only at 0 K and 0 Pa. Moreover, the expressions do not take into account guest–guest interactions. We propose a new more general computational approach to distinguish between promoter molecules capable to form structure sI, sII hydrogen clathrate and those that can form structure H hydrogen clathrate. Our predictive method is based on Gibbs free energy calculations of sI, sII, and sH hydrogen clathrate and thus extends to finite temperatures and pressures.
In Section II we provide computational details. We then in Section III give the results and demonstrate that the van der Waals volume can be used to discriminate between promoters that form hydrogen sI, sII or sH hydrogen clathrate hydrates. We conclude with summary.
II. Computational method
The initial positions of oxygens in sI, sII and in sH are obtained from the experimental X-ray crystallographic clathrate structure as described in ref. 6–9. The Monte Carlo algorithm developed by Buch10 is employed to generate initial proton-disordered configurations according to the ice rules11 and the configuration with dipole moment near zero is selected. The sI 2 × 2 × 2 supercell (24.06 × 24.06 × 24.06 Å3 initial dimensions) consists of 368 water molecules with 48 large and 16 small cages. The fully occupied sI hydrogen clathrate contains 432 molecules. The simulated cell of the sII clathrate hydrate is one unit cell (a = 17.31 Å) containing 136 water molecules in the host framework with 16 small cages and 8 large cages. The total number of molecules in the simulation box of the sII fully filled structure is 160. For the sH clathrate a 2 × 2 × 2 supercell (24.42 × 24.42 × 20.28 Å3) composed of 272 water molecules in the host lattice with 24 small, 16 medium, and 8 large cavities is used. The completely occupied sH clathrate consists of 320 molecules. Single occupancy of any cage of all types of clathrates is assumed. Double occupancy of a single cage is not considered. Complete occupancy of sI, sII, and sH clathrates means that the small and medium cages are occupied by a single H2 molecule whereas the large cages are filled with a promoter molecule, i.e., there are no empty cages left. All molecules are treated as rigid.Molecular interactions are pairwise additive and defined by the Lennard-Jones (LJ) potential for describing the van der Waals interactions. Coulombic long-range electrostatic interactions are treated using the Ewald summation method.12 The intermolecular potential is given by
 | (1) |
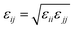 , σij = (σii + σjj)/2 is employed. The Atomic and Bond Contributions method16 was used to calculate van der Waals volume of molecules. Table 1 lists tested promoter molecules with corresponding abbreviations and known experimentally type of formed clathrate structure.
, σij = (σii + σjj)/2 is employed. The Atomic and Bond Contributions method16 was used to calculate van der Waals volume of molecules. Table 1 lists tested promoter molecules with corresponding abbreviations and known experimentally type of formed clathrate structure.
| Abbreviations | Promoter | Molecular formula | Known type formeda |
|---|---|---|---|
| a From ref. 1 and 17–21. | |||
| 2DMB2E | 2,3-Dimethylbut-2-ene | C6H12 | sH |
| 2DMBA | 2,2-Dimethylbutane | C6H14 | sH + H2 |
| 2DMBE | 2,3-Dimethylbutene | C6H12 | sH + H2 |
| 3DMBA | 2,3-Dimethylbutane | C6H14 | sH + H2 |
| 3DMBE | 3,3-Dimethylbutene | C6H12 | sH |
| ACET | Acetylene | C2H2 | sI, sII |
| BUT | Butane (gauche) | C4H10 | sII |
| CBUT | Cyclobutane | C4H8 | sI, sII |
| CDE | Cyclodecane | C10H20 | Unknown |
| CDMC | cis-1,2-Dimethylcyclohexane | C8H16S | sH |
| CHP | Cycloheptane | C7H14 | sH |
| CHX | Cyclohexane | C6H12 | sII + H2 |
| CNO | Cyclononane | C9H18 | Unknown |
| CO | Cyclooctane | C8H16 | sH |
| CP | Cyclopentane | C5H10 | sII + H2 |
| DHF | 2,5-Dihydrofuran | C4H6O | sII + H2 |
| DIO | 1,3-Dioxolane | C3H6O2 | sII + H2 |
| DMBY | 3,3-Dimethylbutyne | C6H10 | sH + H2 |
| DMC | 1,1-Dimethylcyclohexane | C8H16 | sH + H2 |
| DMHP | Dimethylpropane | C5H12 | sII |
| DMP | 3,3-Dimethylpentane | C7H16 | sH + H2 |
| DMPG | 2,2-Dimethylpentane (gauche) | C7H16 | sH |
| FUR | Furane | C4H4O | sII + H2 |
| MB | Methylbutane | C5H12 | sH |
| MCH | Methylcyclohexane | C7H14 | sH + H2 |
| MET | Methane | CH4 | sI, sII |
| MMP | 2-Methoxy-2-methyl-propane | C5H12O | sH + H2 |
| MPROPA | Methylpropane | C4H10 | sII |
| MPROPE | Methylpropene | C4H8 | sII |
| OXE | Oxetane | C3H6O | sI, sII |
| PROP | Propane | C3H8 | sII |
| SHF | Sulfurhexafluoride | SF6 | sII |
| TEMB | Tetramethylbutane | C8H18 | sH |
| THF | Tetrahydrofuran | C4H8O | sII + H2 |
| THP | Tetrahydropyran | C5H10O | sII + H2 |
| TIMB | Trimethylbutane | C7H16 | sH + H2 |
| ETA | Ethane | C2H6 | sI |
| ETE | Ethene | C2H4 | sI |
| FLU | Fluoromethane | CH3F | sI |
Consider the transformation of a fully occupied sII hydrogen clathrate hydrate with a certain promoter in the large cages and hydrogen in the small cages into a fully occupied sH hydrogen clathrate hydrate with the same promoter. The transformation reaction per water molecule is
 | (2) |
Since the chemical potential is given by
 | (3) |
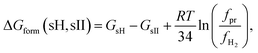 | (4) |
The reaction proceeds to the right if ΔGform(sH, sII) < 0, to the left otherwise. Since bothSsII and SsH are solids the reaction proceeds completion at fixed fugacities of the gaseous and the liquid components.
The fugacity of the promoter component fpr in the liquid phase is calculated using the expression
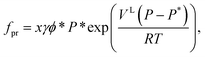 | (5) |
 | (6) |
The fugacity of gaseous hydrogen phase has been obtained from the Virial equation with parameters taken from ref. 24:
 | (7) |
Calculations of the term  in eqn (4) for all promoter compounds from Table 1 and found in ref. 23 demonstrate that the absolute value of the term is almost always less than 0.08 kcal mol−1 which is the error of the free energy difference GsH − GsII. Only for tetrahydrofuran (THF), the modulus of the term is greater than the error and equals to 0.12 kcal mol−1. Therefore, it is a good approximation to neglect the term in eqn (4) and hence
in eqn (4) for all promoter compounds from Table 1 and found in ref. 23 demonstrate that the absolute value of the term is almost always less than 0.08 kcal mol−1 which is the error of the free energy difference GsH − GsII. Only for tetrahydrofuran (THF), the modulus of the term is greater than the error and equals to 0.12 kcal mol−1. Therefore, it is a good approximation to neglect the term in eqn (4) and hence
| ΔGform(sH, sII) = GsH − GsII | (8) |
The expression takes into account all the host–guest and guest–guest interactions. Finite temperature and pressure are taken into consideration by the entropy included in the Gibbs free energy. The sign of the formation free energy in eqn (8) indicates the preference to the formation of either sII hydrogen clathrate or sH hydrogen clathrate. Bearing in mind that GsH and GsII are always negative, hydrogen structure H is energetically favoured to be formed when ΔGform is negative (GsH < GsII). Similarly, when ΔGform(sH, sII) is positive (GsH > GsII), then hydrogen sII hydrogen clathrate is preferably formed.
Similarly, the formation free energy discriminating between crystallization of sH and sI hydrogen clathrate is approximated by
| ΔGform(sH, sI) = GsH − GsI | (9) |
The formation free energy distinguishing between synthesis of sII and sI hydrogen clathrate is expressed as
| ΔGform(sII, sI) = GsII − GsI | (10) |
The self-referential (SR) technique25 is employed for the free energy calculations. The method uses the principle that at fixed volume and temperature the Helmholtz free energy is an extensive quantity and it doubles if the system size doubles. In the SR technique, the absolute Helmholtz free energy is calculated as the free energy difference between two systems with different number of molecules. The SR method consists of two stages: ‘replication’ and ‘relaxation’. The replication stage calculates the free energy difference between the small single-size system and a highly constrained double-size system produced by adding a replica to the original single-size system of interest. The double-size system has twice the Helmholtz free energy of the single-size system of interest. During the relaxation stage this self-similarity constraint applied at the replication stage is gradually relaxed until the molecules do not feel the constraint any more. The relaxation stage is governed by a constraint parameter α. This stage delivers the free energy difference between the fully constrained double-size system and fully relaxed double-size. The double-size system has twice the Helmholtz free energy of the single-size system of interest. Hence the Helmholtz free energy of the crystal of interest is the sum of the free energies differences obtained for the two stages. The Gibbs free energy is obtained via the Helmholtz free energy using the relation G = F + PV.
Simulations in the isothermal isobaric ensemble (NPT) are performed to equilibrate a clathrate at given pressure and temperature. The Helmholtz free energy and configurational energy calculations of empty and fully filled sII and sH clathrate hydrates are conducted in the canonical (NVT) ensemble. Each Monte Carlo (MC) free energy run for a given value of constraint parameter α involves of 400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–700
000–700![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles for equilibration and 60
000 cycles for equilibration and 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–70
000–70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 production cycles for obtaining ensemble averages. Translational and rotational moves are attempted at random with equal probability. Volume trial changes in the NPT simulations occur with frequency 1/N. More theoretical and computational details on the Helmholtz free energy calculations of molecular crystals are provided in ref. 25 and 26.
000 production cycles for obtaining ensemble averages. Translational and rotational moves are attempted at random with equal probability. Volume trial changes in the NPT simulations occur with frequency 1/N. More theoretical and computational details on the Helmholtz free energy calculations of molecular crystals are provided in ref. 25 and 26.
III. Results and Discussion
A. Distinguishing sII and sH clathrates formation
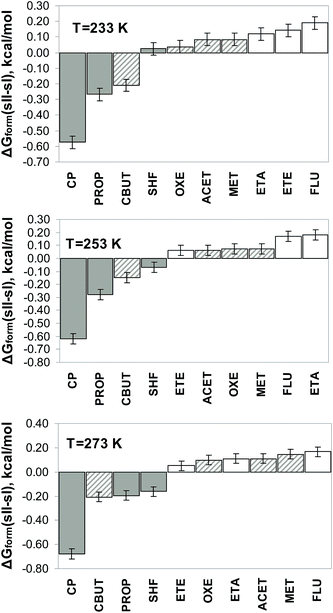
To validate the computational approach for differentiating between guest molecules that can form sH clathrates and molecules that can form sII clathrates, 37 experimentally known promoter molecules have been tested. Structure sII and sH are of special interest of this study because these clathrate types are prospective candidates for hydrogen storage material. The Gibbs free energies of sII and sH hydrogen clathrate hydrates were obtained from self-referential MC simulations at 1000 atm. All small cages of sII and sH clathrates as well as the medium cages of structure H are occupied by single H2. In all large cavities of sII and sH a promoter (experimentally known as either sII or sH former) is inserted to calculate the Gibbs free energies at 233 K, 253 K, and 273 K. The formation free energy ΔGform(sH, sII) is then calculated with eqn (8) for various guest molecules. ΔGform(sH, sII) is depicted in Fig. 1 in an ascending order at the three studied temperatures. Fig. 1 indicates that ΔGform(sH, sII) is always negative (i.e., GsH < GsII) for promoters forming sH clathrate. However, it is worth noting that the formation free energy for sII hydrogen clathrate with cyclohexane (CHX) at 253 K and dimethylpropane (DMPH) and methylpropene (MPROPE) at 273 K is smaller than the error bar. The proposed computational approach for predicting the type of clathrate structure (either sII or sH) to be formed by a potential promoter molecule, demonstrates excellent agreement with experimental evidences.The order of the formation free energies for different promoters seen in Fig. 1 cannot be altered with the change of pressure. The preference for formation of a particular type of clathrate (sII or sH) cannot be facilitated by pressure either. This is demonstrated at 233 K in Fig. 2 by showing ΔGform(sH, sII) at 75 MPa, 50 MPa, 25 MPa, and 101 MPa.
 | ||
| Fig. 2 At 233 K formation free energy for selected tested promoter molecules at 75 MPa, 50 MPa, and 25 MPa. Errors are to two standard deviations. | ||
B. Dependence on volume
At all studied temperatures it has been observed that the van der Waals volume (Vvwd) of enclathrated promoter molecule is a very important parameter in screening potential molecules capable to form either sII or sH hydrogen clathrates. Fig. 3 demonstrates the formation free energy versus the van der Waals volume of known promoters forming sII and sH clathrates. | ||
| Fig. 3 Formation free energy as a function of the van der Waals volume of tested promoter molecules at 1000 atm and 233 K, 253 K, and 273 K. | ||
Fig. 3 confirms computational study5 and an experimental rule of thumb that at all studied temperatures there is a rough threshold of Vvwd of the promoter which separates secondary guest molecules forming sII clathrates from those known as sH clathrate formers. This is found to be the case at all temperatures considered even though the relative stability of the hydrates of different promoters alters with temperature. Nonetheless, it is worth noting that as the van der Waals volumes of sH and sII formers overlap, there is no definite threshold which able to predict type of formed clathrate. The same conclusion has been reached in ref. 5.
C. Distinguishing sI and sII clathrates formation
To put this method further to the test we also tried to distinguish between formation of sI and sII clathrates. To determine whether sI type hydrogen clathrate can be formed by a specific promoter molecule, additional calculations of formation free energy ΔGform(sH, sI) and ΔGform(sII, sI) using eqn (9) and (10) are required. The clathrate with the lowest formation free energy would be the type predicted. Fig. 4 demonstrates ΔGform(sII, sI) for ten selected promoter molecules at three different temperatures. In comparison with ΔGform(sH, sII) and ΔGform(sH, sI), the formation free energies ΔGform(sII, sI) for these chosen ten promoter at studied temperatures have the lowest value and hence, determine whether either sII or sI type of clathrate would be crystallized. In Fig. 4 ΔGform(sII, sI) for cyclopentane (CP), propane (PROP), and sulfurhexafluoride (SHF) demonstrates preference for sII type hydrogen clathrate formation at all temperatures, except at 233 K when it is positive, however, the formation free energy at that temperature is smaller than the error bar. ΔGform(sII, sI) is always positive for ethane (ETA), ethene (ETE), and fluoromethane (FLU) that confirms that sI hydrogen clathrates are synthesized with help of those promoters. Acetylene (ACET), cyclobutane (CBUT), methane (MET), and oxetane (OXE) compounds can form both sI and sII clathrates and ΔGform(sII, sI) can be both positive and negative to still agree with experiments. Fig. 4 shows very good agreement with experimental information on the clathrate type formed by a selected promoter. It is also encouraging to see that at the lowest temperature, ΔGform(sII, sI) of the clathrates which can form both sI and sII types mostly fall in between the values of sI and sII formers.To the best our knowledge compounds cyclononane (CNO) and cyclodecane (CDE) have not been tested for synthesizing clathrate hydrates experimentally. Our calculations have shown that at all temperatures the formation free energy ΔGform(sH, sII) for these compounds is always negative (Fig. 1). We therefore propose CNO and CDE as potential candidates for sH hydrogen clathrates formers. In a previous computational study27 we have shown that the stability of sH hydrogen clathrate hydrates with these two promoter molecules demonstrates an unusually strong temperature dependence, which can be exploited if easy release of hydrogen is required.
IV. Conclusions
We have presented and validated a computational method for predicting a type (either sI or sII or sH) of hydrogen clathrate which can be formed by a particular promoter. The method is based on the Gibbs free energy calculations and is valid at finite temperatures and pressures. It has been found that the van der Waals volume of a potential promoter is an important parameter which can determine a type (either sII or sH) of clathrate to be formed. It has been found that it is impossible to change a type of hydrogen clathrate structure by decreasing/increasing pressure imposed on the clathrate. At all studied temperatures there is a rough threshold of the van der Waals volume of entrapped promoter molecule which distinguishes promoter molecules capable to form sII clathrates from those forming sH clathrates. Our formation free energy calculations indicate that the promoters in Table 1 known as formers of pure sI or sII or sH clathrates formers can form corresponding hydrogen clathrates. However, this requires experimental verification.Acknowledgements
We would like to thank Prof. G.J. Kroes for discussions. A.A.A and H.M.C. are grateful for support from the VIDI research programme 700.10.427, which is financed by the Netherlands Organisation for Scientific Research (NWO). H.M.C. acknowledges the European Research Council (ERC-2010-StG, Grant Agreement no. 259510-KISMOL) for financial support.References
- E. D. Sloan and C. A. Koh, Clathrate Hydrates of Natural Gases, CRC Press, Boca Raton, FL, 3rd edn, 2008 Search PubMed.
- Y. A. Dyadin, E. G. Larionov, A. Y. Manakov, F. V. Zhurko, E. Y. Aladko, T. V. Mikina and V. Y. Komarov, Mendeleev Commun., 1999, 9, 209–210 CrossRef PubMed.
- W. L. Mao and H. K. Mao, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 708–710 CrossRef CAS PubMed.
- L. J. Florusse, C. J. Peters, J. Schoonman, K. C. Hester, C. A. Kho, S. F. Dec, K. N. Marsh and E. D. Sloan, Science, 2004, 306, 469–471 CrossRef CAS PubMed.
- T. J. Frankcombe and G. J. Kroes, Phys. Chem. Chem. Phys., 2011, 13, 13410–13420 RSC.
- R. K. Mcmullan and G. A. Jeffrey, J. Chem. Phys., 1965, 42, 2725–2732 CrossRef CAS PubMed.
- E. P. Klaveren, J. P. J. Michels, J. A. Schouten, D. D. Klug and J. S. Tse, J. Chem. Phys., 2001, 114, 5745–5754 CrossRef PubMed.
- E. P. Klaveren, J. P. J. Michels, J. A. Schouten, D. D. Klug and J. S. Tse, J. Chem. Phys., 2001, 115, 10500–10508 CrossRef PubMed.
- E. P. Klaveren, J. P. J. Michels, J. A. Schouten, D. D. Klug and J. S. Tse, J. Chem. Phys., 2002, 117, 6637–6645 CrossRef PubMed.
- V. Buch, P. Sandler and J. Sadlej, J. Phys. Chem. B, 1998, 102, 8641–8653 CrossRef CAS.
- D. Eisenberg and W. Kauzmann, The Structures and Properties of Water, Oxford University Press, Oxford, U.K, 1969 Search PubMed.
- B. Smit and D. Frenkel, Understanding Molecular Simulation: From Algorithms to Applications, Academic Press, New York, 2nd edn, 2001 Search PubMed.
- J. L. F. Abascal and C. Vega, J. Chem. Phys., 2005, 123, 234505–234516 CrossRef CAS PubMed.
- S. Alavi, J. A. Ripmeester and D. D. Klug, J. Chem. Phys., 2006, 124, 014704–014709 CrossRef PubMed.
- W. D. Cornell, P. Cieplak, C. L. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 5179–5197 CrossRef CAS.
- Y. H. Zhao, M. H. Abraham and A. M. Zissimos, J. Org. Chem., 2003, 68(19), 7368–7373 CrossRef CAS PubMed.
- J. A. Ripmeester and C. I. Ratcliffe, J. Phys. Chem., 1990, 94, 8773–8776 CrossRef CAS.
- J. A. Ripmeester, C. I. Ratcliffe, D. D. Klug and J. S. Tse, Ann. N. Y. Acad. Sci., 1994, 715, 161–176 CrossRef CAS PubMed.
- G. A. Jeffrey and R. K. McMullan, Prog. Inorg. Chem., 1967, 8, 43–108 CrossRef CAS PubMed.
- A. R. C. Duarte, A. Shariati and C. J. Peters, J. Chem. Eng. Data, 2009, 54, 1628–1632 CrossRef CAS.
- A. T. Trueba, L. J. Rovetto, L. J. Florusse, M. C. Kroon and C. J. Peters, Fluid Phase Equilib., 2011, 307, 6–10 CrossRef CAS PubMed.
- B. E. Poling, J. M. Prausnitz and J. P. O'Connell, The Properties of Gases and Liquids, McGraw-Hill, New York, 5th edn, 2001 Search PubMed.
- K. Kojima, S. Zhang and T. Hiaki, Fluid Phase Equilib., 1997, 131, 145–179 CrossRef CAS.
- R. D. McCarty, Hydrogen Technological Survey – Thermophysical Properties, Scientific and Technical Information Office, NASA, Washington, D.C., 1975 Search PubMed.
- A. A. Atamas, M. V. Koudriachova, S. W. de Leeuw and M. B. Sweatman, Mol. Simul., 2011, 37(4), 284–292 CrossRef CAS PubMed.
- A. A. Atamas, H. M. Cuppen, M. V. Koudriachova and S. W. de Leeuw, J. Phys. Chem. B, 2013, 117, 1155–1165 CrossRef CAS PubMed.
- A. A. Atamas, M. V. Koudriachova, S. W. de Leeuw and H. M. Cuppen, J. Phys. Chem. C, 2014, 118, 22211–22220 CAS.
| This journal is © The Royal Society of Chemistry 2015 |