Constitutive modeling of the viscoelastic mechanical response of foam rubber-like materials
Abstract
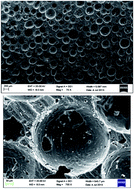
The viscoelastic mechanical behavior of foam rubber-like materials under large deformation is studied using thermodynamic methods. Because the strain energy function can be additively split into deformation energy and volume energy, the deformation of materials is decomposed into volumetric deformation and isochoric deformation. A nonlinear viscoelastic constitutive model for large deformation of foam rubber-like materials is established in this paper. The nonlinear viscoelastic mechanical responses of foam rubber-like materials under several common loading conditions are calculated by the new proposed constitutive model.

 Please wait while we load your content...
Please wait while we load your content...