Superhard-driven search of the covalent network in the B₃NO system

Abstract

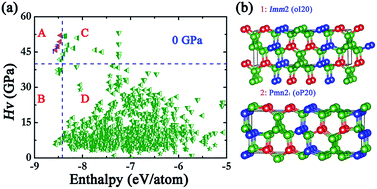
The search for new superhard materials with a Vickers hardness larger than 40 GPa remains a considerable experimental and theoretical challenge. Here, we perform a superhard-driven search using an unbiased structure search method based on the CALYPSO method in the ternary B–N–O system, B₃NO, which is isoelectronic with diamond. A variety of newly predicted structures of the B₃NO compound with short, strong, and three-dimensional covalent bonds were designed. Among them, two newly predicted orthorhombic structures with Imm2 (oI20) and Pmn2₁ (oP20) space groups were found to be superhard and energetically stable. After examining the dynamical stabilities, we found that these two structures are energetically more preferable. Further hardness calculations showed that the two structures are superhard materials with a Vickers hardness above 45 GPa, exceeding the criterion of superhard materials. The electronic results show that the oI20 and oP20 structures are semiconductor materials with an optimal band gap of 0.87 and 0.12 eV, respectively. The present results reveal that the B₃NO compounds can be used as superhard materials or narrow band-gap semiconductor materials, and therefore have broad prospects in industrial applications, and also provide insights for exploring other functional compounds with a functionality-driven design.

---

1. Introduction

Superhard materials play an important role in a variety of industrial applications, e.g. from cutting and polishing tools to wear-resistant coatings.¹ It is well known that diamond is the hardest known material with a hardness from 60 to 120 GPa² measured experimentally. However, it is limited by several shortcomings, including brittleness, easily reacting with iron-containing materials and oxidization in air under high temperature. An immense amount of experimental and theoretical studies have been devoted to searching for new superhard materials with greater thermal stability and inert chemical activity.^3–6 Traditionally, it is commonly accepted that superhard materials are formed by light elements (B, C, N and O), since they contain short and strong covalent bonds providing resistance to both elastic and plastic deformations e.g., c-BN,⁷ C₃N₄,⁸ B₂O,^9,10 BC₂N,^11–17 B₂CO,¹⁸ and BC₃.^19,20 Note that previous studies have already demonstrated that diamond-like superhard c-BN⁷ and B₂O^9,10 compounds can form typical sp³ covalent B–N and B–O bonds. It is reasonable to suppose that materials with mixed B–N and B–O bonds may possess a covalent bond network, resulting in high hardness. It is noteworthy that B₃NO has 20 valence electrons per formula unit (4 valence electrons per atom) and is thus isoelectronic with diamond (they have the same number of valence electrons per atom). Isoelectronic compounds always have similar chemical bonds and structural properties. Therefore, it is expected that B₃NO would form typical strong covalent sp³ bonds, which are necessary for superhard materials.

The search for candidate structures is critical to understand the hardness and related physical properties of B₃NO. In this work, we have predicted various structures for B₃NO under 0–100 GPa with the superhard-driven CALYPSO method, which is a developed methodology for designing superhard materials for given chemical systems under high pressure. It is in contrast to the traditional ground-state prediction method where the total energy is solely used as the fitness function. We adopted hardness as the fitness function in combination with the first-principles method to construct the hardness vs. energy map by seeking a proper balance between hardness and energy for a better mechanical description of given chemical systems. We predicted a variety of structures with high hardness and relatively low energy. Two energetically stable structures were uncovered in our structure searches consisting of strong covalent B–B, B–N and B–O bonds. The calculations show that they are superhard materials with a Vickers hardness above 45 GPa. Our current work significantly improves the understanding of superhard-driven predictions and also reveals that B₃NO compounds behave as both superhard and photocatalytic materials, which have wide potential for industrial applications.

2. Computational details

Our global structural prediction uses the unbiased intelligence based on the CALYPSO (Crystal structure AnaLYsis by Particle Swarm Optimization) method^21–23 which has successfully predicted structures for various systems ranging from elemental solids to binary and ternary compounds.^24–29 The main characteristic of CALYPSO is the functionality-driven design of novel functional materials, e.g., superhard, superconducting, and semiconductor materials. The electron–ion interaction was described by means of the projector augmented wave (PAW)³⁰ with 2s²2p¹, 2s²2p³ and 2s²2p⁴ electrons as valence for B, N and O atoms, respectively. The structural relaxations, electron localization function (ELF) and electronic band structure calculations were performed using the density functional theory within the local density approximation (LDA)^31,32 as implemented in the Vienna ab initio simulation package (VASP) code.³³ The energy cutoff of 520 eV was adopted to give excellent convergence on the total energies and structural parameters. Monkhorst–Pack (MP) k meshes³⁴ 0.03 Å⁻¹ were chosen to ensure that all structures were well converged to better than 1 meV per formula. The phonon frequencies were calculated using the direct supercell method. This method uses the forces obtained by the Hellmann–Feynman theorem calculated from the optimized supercell.³⁵ Accurate crystal elastic constants and moduli were calculated by the Voigt–Reuss–Hill approximation.³⁶ The micro-hardness model^23,37,38 based on bond strength was used for the hardness calculation. It is worth mentioning that the Laplace matrix was introduced to consider the anisotropy²³ for the hardness calculation. The calculations of Mulliken population were carried out with the CASTEP plane-wave code.³⁹

3. Results and discussion

Variable cell simulations of B₃NO were performed at 0–100 GPa with 1–4 formula units (f.u.) per unit cell. The calculated hardness vs. enthalpy map is shown in Fig. 1 at 0 and 100 GPa. Every point on the map represents one predicted B₃NO structure. We divide the map into four parts indicated by A, B, C and D by taking Hv = 40 GPa as the horizontal reference line and the enthalpy (−8.42 and −4.87 eV per atom for 0 and 100 GPa, respectively) of B₂O (P4̄m2)¹⁰ and c-BN⁷ for the vertical reference line, which have been experimentally synthesized. Our target area is area A, which possesses desirable hardness and competitive low energies. Energetically, all the structures in area A are most likely to be synthesizable and might be potential superhard materials. The structures in area B are not good candidates for superhard materials, but they might also be synthesizable. Structures in C and D are energetically very unfavorable and thus should be ruled out. In this work, we chose four typical structures with negative formation enthalpies (in area A), which possess the lowest enthalpy, and the highest hardness. As shown in Fig. 1, the most stable structure is an orthorhombic structure with an Imm2 space group and contains 20 atoms, which is marked as oI20 (orthorhombic, Imm2, 20 atoms per f.u.) and the structure with the highest hardness is an orthorhombic structure Pmm2 (oP5). The second most stable one (orthorhombic structure with a Pmn2₁ space group, oP20) and the one with the second-highest hardness value (hexagonal structure with a P3m1 space group, hP5) were also studied for comparison. The enthalpy curves for these structures relative to the c-BN and B₂O structure are plotted in Fig. 2. The formation enthalpy (ΔE) is defined as ΔE = E(B₃NO) − E(B₂O) − E(BN). It is clearly seen that these structures are energetically more stable than B₂O¹⁰ and c-BN⁷ at pressures ranging from 0 to about 83 GPa. The oI20 structure is 45.3 meV per atom lower in energy than the oP20 structure at 0 GPa.

Fig. 1 The hardness vs. enthalpy map of B₃NO constructed by superhard-driven calculations based on the CALYPSO method. All the predicted structures are shown at 0 GPa (a) and 100 GPa (b). The four areas indicated by A, B, C and D are divided by taking Hv = 40 GPa as the horizontal reference line and the total enthalpy (−8.42 eV and −4.87 eV for 0 and 100 GPa, respectively) of B₂O¹⁰ and c-BN⁷ for the vertical reference line.

Fig. 2 Calculated enthalpy versus pressure for these representative structures relative to that of the c-BN⁷ and B₂O.¹⁰

All four structures stabilize in a three-dimensional network with typically strong covalent B–B, B–N, and B–O bonds (Fig. 3). It was found that all these structures are made up of rings with different atom numbers. The most stable oI20 structure comprises irregular 6-member rings, while oP20 is formed by 4-numbered, 6-numbered, and 8-numbered rings. Both hP5 and oP5 are made up by 6- and 8-numbered rings. At zero pressure, for the oI20 structure, the lattice parameters take a = 11.5486 Å, b = 2.5757 Å, and c = 4.1712 Å, with atomic positions of B1 at Wyckoff 2a (0, 0, 0.1567), B2 at 2b (0, 0.5, 0.4433), B3 at 4c (0.2210, 0, 0.0802), B4 at 4c (0.0899, 0, 0.5845), N at 4c (0.2165, 0, 0.4535), and O at 4c (0.3974, 0.5, 0.4440); for oP5, the lattice parameters are a = 2.5394 Å, b = 2.4362 Å, and c = 5.2887 Å, with atomic positions of B1 at 1a (0, 0, 0.0863), B2 at 1b (0, 0.5, 0.6477), B3 at 1d (0.5, 0.5, 0.4267), N at 1c (0.5, 0, 0.2500), and O at 1b (0, 0.5, 0.9224); for oP20, the lattice parameters are a = 2.5746 Å, b = 11.5431 Å, and c = 4.2533 Å, with atomic positions of B1 at 2a (0, 0.7500, 0.0747), B2 at 2a (0, 0.0243, 0.0974), B3 at 2a (0, 0.4710, 0.9354), B4 at 2a (0, 0.1646, 0.4300), B5 at 2a (0, 0.3402, 0.4297), B6 at 2a (0.5, 0.7501, 0.3605), N1 at 2a (0, 0.0271, 0.4616), N2 at 2a (0, 0.4662, 0.5619), O1 at 2a (0.5, 0.8464, 0.5768), and O2 at 2a (0.5, 0.6467, 0.5720); for hP5, the lattice parameters are a = b = 2.5915 Å, and c = 5.7107 Å, with atomic positions of B1 at 1a (0, 0, 0.8670), B2 at 1a (0, 0, 0.3382), B3 at 1b (0.3333, 0.6667, 0.6954), N at 1b (0.3333, 0.6667, 0.4373), and O at 1a (0, 0, 0.0961).

Fig. 3 Structures for B₃NO: oI20 (a), oP5 (b), oP20 (c), and hP5 (d), respectively. The dark solid lines denote the unit cells. The B, N and O atoms are represented as green, blue and red spheres, respectively.

As potential candidates for superhard materials, the mechanical properties of the four structures are important for industrial applications. The calculated bond length, density (ρ), bulk modulus (B), shear modulus (G) and hardness (Hv) of these four typical structures are given in Table 1. For the orthogonal and hexagonal structures, the mechanical stability requires the elastic constants to satisfy the following conditions: C_ii > 0 (i = 1–6), C₁₁ + C₂₂ + C₃₃ + 2(C₁₂ + C₁₃ + C₂₃) > 0, C₁₁ + C₂₂ − C₁₂ > 0, C₁₁ + C₃₃ − 2C₁₃ > 0, C₂₂ + C₃₃ − C₂₃ > 0, and C₄₄ > 0, C₁₁ > C₁₂, (C₁₁ + 2C₁₂) × C₃₃ > 0, respectively. It is clear from Table 2 that the whole set of elastic constants of these four structures satisfy the above conditions, indicating mechanical stability. The structures listed in Table 1 exhibit high bulk moduli of 284–332 GPa, indicating the structures are difficult to compress near their respective equilibrium volumes. The values have been significantly enlarged when compared to B₂O (∼240 GPa). From the analysis of the bonding environment of these crystal structures, both the B₃NO and B₂O structures adopt clear sp³ hybridizations, but B₃NO forms additional B–N bonds besides the B–B and B–O bonds. For comparison, here we give the bond lengths of referenced B₂O¹⁰ and c-BN⁷ of 1.670 Å (B–B), 1.565 Å (B–N), 1.503, and 1.488 Å (B–O). Obviously, the B–N bond in B₃NO is much shorter than the B–B and B–O bonds in B₂O, giving stronger covalent bonds in B₃NO. The ratio between the bulk modulus (B) and shear modulus (G) can be used to predict the brittle or ductile behavior of materials. The calculated B/G for these structures reaches 1.07–1.27, which is smaller than the criteria of 1.75 (ref. 40) (ductile behavior is predicted when B/G > 1.75, otherwise the material behaves in a brittle manner). It is imperative to check the phonon spectra of all four structures, since they provide crucial information on the structural stabilities. No imaginary frequency in the whole first Brillouin zone is a necessary condition to ensure the predicted structure can physically exist. From the calculated phonon dispersions, oI20 and oP20 [shown in Fig. 4(a) and (b), respectively] are dynamically stable at 0 GPa. However, hP5 and oP5 are dynamically unstable [shown in Fig. 4(c) and (d), respectively], thereby ruling out the possibility of being synthesized.

Table 1 The calculated bond length, density (ρ), bulk modulus (B), shear modulus (G) and hardness (Hv) of the predicted four typical superhard structures

Structure	Bond length (Å)			ρ (g cm^−3)	B (GPa)	G (GPa)	Hv (GPa)
	B–O	B–N	B–B
oI20	1.480, 1.507	1.558, 1.560, 1.568	1.756, 1.757	3.342	332	310	45.9
oP5	1.453, 1.495	1.535, 1.537	1.725	3.169	303	245	52.1
oP20	1.443, 1.477, 1.495, 1.508, 1.529	1.530, 1.549, 1.560, 1.572, 1.589, 1.593	1.734, 1.766, 1.770	3.281	326	296	47.4
hP5	1.308, 1.383	1.474, 1.600	1.789	3.122	284	223	49.4

---

Table 2 The calculated elastic constants C_ij (GPa) of the predicted four typical superhard structures

Structure	C11	C22	C33	C44	C55	C66	C12	C13	C23
oI20	878	642	743	352	311	287	99	129	152
oP5	536	779	869	333	284	139	37	145	148
oP20	835	833	699	241	255	312	174	77	46
hP5	1422		435	140			49

---

Fig. 4 The phonon dispersion of oI20 (a), oP5 (b), oP20 (c), and hP5 (d) at 0 GPa.

To further understand the electronic properties, we performed simulations on the electronic band structure and partial density of states (PDOS) of oI20 and oP20, as shown in Fig. 5. The calculated results reveal the semiconductor features of these two structures with indirect band gaps of 0.87 and 0.12 eV, respectively. Since density functional calculations typically underestimate the gap by 30–50%, the true band gap might be in the range of 1.24–1.74 eV and 0.17–0.24 eV, respectively. The electronic states near the Fermi level are mainly contributed by B-2p and a few N-2p, and O-2p states. The partial DOS profiles for B-2p, N-2p and O-2p are very similar from −12 to −4 eV, reflecting the significant hybridizations between these orbitals and strong covalent interactions in both the B–N and B–O bonds.

Fig. 5 Band structure (left) and the partial density of states (right) of the oI20 (a), and oP20 (b) structures at ambient pressure.

Finally, we examined the charge density distribution and the ELF that enables an effective and reliable analysis of the nature of the covalent bonding. It is useful in distinguishing ionic, covalent, and metallic bonding. Here, we used the isosurface value of 0.83 as a high ELF (≥0.8) indicates the formation of strong covalent bonds.^41,42 High electron localization can be seen in the region between adjacent B–B, B–N, and B–O bonds, indicative of strong covalent bonding (Fig. 6). Also the calculated overlap population of the B–B, B–N, and B–O bonds as shown in Table 3 is high, indicating that oI20 and oP20 are strong covalent solids. The calculated ELF shows that the O atoms in oI20 and oP20 structures are threefold coordinated with three near-neighbor B atoms and a lone pair of electrons. It is clearly seen that the electronic state is actually characterized by the 3D tetrahedral-like electronic state similar to that of the nitrogen atoms in bct-CN₂.⁴³ The N atoms are four fold-coordinated and form a stable sp³ bonding state. However, the bonding environment of the boron atoms is more complex. Boron has three valence electrons, and is electron deficient compared with carbon. The 2D ELF, 3D ELF, and the coordination numbers of the B atoms are given in order to show a clear point of view. The B1 atoms in oI20 and B3 atoms in oP20 are six fold-coordinated with six neighboring boron atoms. Other boron atoms are four fold-coordinated and form a stable sp³ bonding state with boron, nitrogen and oxygen atoms. The bonding states of oI20 are similar to that of oP20 as clearly shown in the 2D ELF. These strong three-dimensional covalent bonds could reasonably explain the superhardness properties of the oI20 and oP20 structures. Our current research reveals that B₃NO simultaneously belongs to superhard and semiconductor materials and, therefore, may have wide application prospects in industry, such as in cutting tools, coating materials, photocatalytic materials, and so on. In addition, the present work has opened up a new route to search for functional materials.

Fig. 6 Contours of the ELF of oI20 (a), (b) and oP20 (c), (d) with the isosurface = 0.83. The coordination numbers of the boron atoms are given for better observation.

Table 3 The calculated Mulliken population of the oI20 and oP20 structures

oI20			oP20
Bond	Population	Length (Å)	Bond	Population	Length (Å)
B–O	0.59	1.4802	B–O	0.64	1.4429
	0.61	1.4807		0.61	1.4774
	0.40	1.5067		0.58	1.4947
				0.53	1.4957
				0.38	1.5077
				0.42	1.5292
B–N	0.55	1.5580	B–N	0.79	1.5304
	0.58	1.5608		0.47	1.5492
	0.75	1.5681		0.58	1.5599
				0.75	1.5723
				0.55	1.5895
				0.44	1.5933
B–B	0.62	1.7560	B–B	0.64	1.7341
	0.54	1.7572		0.61	1.7664
				0.53	1.7706

---

4. Conclusions

In conclusion, we have extensively explored structures of B₃NO with a superhard-driven purpose based on CALYPSO methodology. The calculated hardness vs. enthalpy maps provide a variety of newly predicted structures of B₃NO compounds containing short, strong, and three-dimensional covalent bonds. Interestingly, we uncovered two energetically stable B₃NO structures (oI20 and oP20) possessing very high hardness values. No imaginary phonon frequencies were observed indicating they are dynamically stable at 0 GPa. They are three-dimensional orthorhombic structures with space groups of Imm2 and Pmn2₁ (oI20 and oP20). The calculated elastic constants and moduli indicate these two structures are very incompressible as expected from their short and strong 3D chemical bonding. The calculated Vickers hardness of the oI20 and oP20 phases reaches 45.9 and 47.4 GPa with an indirect band gap of 0.87 and 0.12 eV, respectively. Our current results are helpful for improving the understanding of a functional-driven search and thus could stimulate future experimental synthesis and determination of B₃NO.

Acknowledgements

This work is supported by the China 973 Program (2011CB808200), the Natural Science Foundation of China under 51202084, 11474125, and 11274136, the 2012 Changjiang Scholars Program of China, Changjiang Scholar and Innovative Research Team in University (IRT1132). Parts of the calculations were performed in the High Performance Computing Center (HPCC) of Jilin University.

References

1. J. Bocquillon, Annu. Rev. Mater. Sci., 2001, 31, 1.
2. V. Brazhkin, N. Dubrovinskaia, A. Nicol, N. Novikov, R. Riedel, V. Solozhenko and Y. Zhao, Nat. Mater., 2004, 3, 576.
3. Q. Li, H. Wang and Y. Ma, J. Superhard Mater., 2010, 32, 192.
4. Y. Tian, B. Xu and Z. Zhao, Int. J. Refract. Met. Hard Mater., 2012, 33, 93.
5. O. O. Kurakevych, J. Superhard Mat., 2009, 31, 139.
6. B. Xu and Y. Tian, Sci. China Math., 2015, 58, 132.
7. R. H. Wentorf, J. Chem. Phys., 1957, 26, 956.
8. G. M. Rignanese, J. C. Charlier and X. Gonze, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 205416.
9. D. He, Y. Zhao, L. Daemen, J. Qian, T. D. Shen and T. W. Zerda, Appl. Phys. Lett., 2002, 81, 643.
10. Q. Li, W. Chen, Y. Xia, Y. Liu, H. Wang, H. Wang and Y. Ma, Diamond Relat. Mater., 2011, 20, 501.
11. Z. Pan, H. Sun and C. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 174115.
12. Q. Li, M. Wang, A. R. Oganov, T. Cui, Y. Ma and G. Zou, J. Appl. Phys., 2009, 105, 053514.
13. S. Nakano, M. Akaishi, T. Sasaki and S. Yamaoka, Chem. Mater., 1994, 6, 2246.
14. E. Knittle, R. B. Kaner, R. Jeanloz and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 12149.
15. T. Komatsu, M. Nomura, Y. Kakudate and S. Fujiwara, J. Mater. Chem., 1996, 6, 1799.
16. V. L. Solozhenko, D. Andrault, G. Fiquet, M. Mezouar and D. C. Rubie, Appl. Phys. Lett., 2001, 78, 1385.
17. Y. Zhang, H. Sun and C. Chen, Phys. Rev. Lett., 2004, 93, 195504.
18. Y. Li, Q. Li and Y. Ma, Europhys. Lett., 2011, 95, 66006.
19. M. Zhang, H. Liu, Q. Li, B. Gao, Y. Wang, H. Li, C. Chen and Y. Ma, Phys. Rev. Lett., 2015, 114, 015502.
20. P. Zinin, L. Ming, H. Ishii, R. Jia, T. Acosta and E. Hellebrand, J. Appl. Phys., 2012, 111, 114905.
21. Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063 , CALYPSO code is free for academic use. http://www.calypso.cn.
22. Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116.
23. X. Zhang, Y. Wang, J. Lv, C. Zhu, Q. Li, M. Zhang, Q. Li and Y. Ma, J. Chem. Phys., 2013, 138, 114101.
24. H. Liu and Y. Ma, Phys. Rev. Lett., 2013, 110, 025903.
25. J. Lv, Y. Wang, L. Zhu and Y. Ma, Phys. Rev. Lett., 2011, 106, 015503.
26. L. Zhu, H. Wang, Y. Wang, J. Lv, Y. Ma, Q. Cui, Y. Ma and G. Zou, Phys. Rev. Lett., 2011, 106, 145501.
27. Q. Li, D. Zhou, W. Zheng, Y. Ma and C. Chen, Phys. Rev. Lett., 2013, 110, 136403.
28. S. Lu, Y. Wang, H. Liu, M. Miao and Y. Ma, Nat. Commun., 2014, 5, 3666.
29. L. Zhu, H. Liu, C. J. Pickard, G. Zou and Y. Ma, Nat. Chem., 2014, 6, 644.
30. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
31. D. M. Ceperley and B. Alder, Phys. Rev. Lett., 1980, 45, 566.
32. J. Ihm, A. Zunger and M. L. Cohen, J. Phys. C: Solid State Phys., 1979, 12, 4409.
33. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
34. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188.
35. A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106.
36. R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349.
37. A. Šimůnek and J. Vackář, Phys. Rev. Lett., 2006, 96, 085501.
38. A. Šimůnek, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 172108.
39. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567.
40. S. Pugh, Philos. Mag., 1954, 45, 823.
41. A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397.
42. B. Silvi and A. Savin, Nature, 1994, 371, 683.
43. Q. Li, H. Liu, D. Zhou, W. Zheng, Z. Wu and Y. Ma, Phys. Chem. Chem. Phys., 2012, 14, 13081.

---