Kinetic and mechanistic investigations of the thermal decomposition of methyl-substituted cycloalkyl radicals†
Abstract
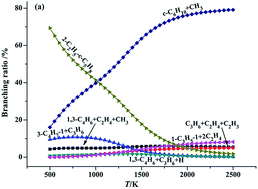
A systematic theoretical study on the thermal decomposition of 2-Me-cyclobutyl, 2-Me-cyclopentyl and 2-Me-cyclohexyl radicals is performed using the high-level ab initio CBS-QB3 and CCSD(T) quantum chemical calculations. The calculation reveals that the detailed reaction mechanism of the thermal decomposition of these cyclic alkyl radicals incorporates ring opening, vinyl rearrangements (exocyclization), beta-site C–C bond cleavage and H-elimination processes. The standard reaction enthalpies (ΔrH0298) and Gibbs free energies (ΔrG0298) for each elementary reaction involved in the 2-Me-cyclohexyl radical reactive system are also determined with the composite CBS-QB3 method. All the investigated vinyl rearrangements reactions are exothermic and spontaneous, while the ring opening, C–C bond scission and H-elimination processes are endothermic and nonspontaneous. Among all the investigated elementary reactions, the exocyclization processes are kinetically accessible and readily proceed (due to their significantly lower barrier and they are highly exothermic). Compared with the barrier heights for the distinct vinyl rearrangement pathways in these cyclic alkyl radicals, it can be found that they decrease in the order of 1,3- > 1,2- > 1,4-vinyl transfer. The branching ratios are evaluated at different temperatures on the basis of the quasi-steady state approximation (QSSA). The calculated result shows that the 1,2-, 1,3- and 1,4-vinyl rearrangement reactions are advantaged at low temperature, while the formation of a cycloalkene is favoured at high temperature.

 Please wait while we load your content...
Please wait while we load your content...