Digitization of two-phase flow patterns in a microchannel induced by an external AC field
Abstract
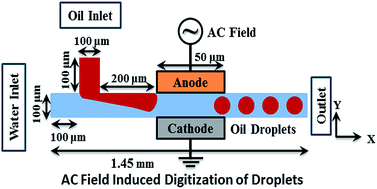
An externally applied alternating current (AC) electrostatic field can deform the interface of a pair of weakly conducting liquids to engender droplet flow patterns inside the ‘T’ shaped microchannels. The electrohydrodynamic stresses originating from the accumulation of free and induced charges at the interface of the immiscible liquids stimulate the formation of droplets with higher surface to volume ratio. Strikingly, the size, shape, and frequency of the flow patterns can be tuned by varying the frequency and waveform of the external AC field. The enhanced dielectrophoretic force at a higher field intensity and lower frequency of the AC field facilitates the formation of droplets with smaller size and higher throughput. The size, shape, and frequency of the droplets are also found to be functions of the ratio of the electrical conductivity of the phases and the interfacial tension. The proposed methodology demonstrates a non-invasive pathway to digitize the flow patterns inside a multiphase microfluidic device with the help of an external AC field.

 Please wait while we load your content...
Please wait while we load your content...