The constitutive behavior of ammonium ionic liquids: a physiochemical approach

Abstract

A huge number of possible molecular variants often forms a puzzle about their identity and integrity to processes, which can be resolved by adopting a concrete selection procedure of significance. This further relies on its relation with some phenomena on microscopic structure and macroscopic behavior. This study recognizes the numerous approaches to answer it on the grounds of thermodynamics for Ionic Liquids (ILs) and the conception of a middleman in the additivity phenomenon through molecular tailoring and a validated dataset, wherein Wada’s theory for molecular compressibility, A, is found inconsistent and is thus redefined. ILs are found to be divergent into two groups, depending upon the cationic integration rather than the anionic, on close analysis of the molecular sound velocity, R, to the molecular weight. Moreover, the study presents ILs in contrast to molecular fluids and presents their physiochemical nature in terms of Jacobson’s relation and Mark’s study on molecular fluids. The applicability of the Newton–Laplace relation has also been deduced. The missing links in persisting theories are explored quantitatively and structural descriptors are estimated for structural variability of –CH₂/–CH₃ commonly found in ILs. It seems quite interesting to visualize the appendages like benzyl, methylene and methyl in the molecular skeleton being the source of drastic effects on the studied behaviors. By far, these can, more or less, aid in solving the molecular puzzle of accessing ionic liquids’ potential of structural variability for task-specific applications, such as fluid mechanics, organic synthesis, reaction kinetics, antimicrobial activity and CO₂ capture and sequestration.

---

Introduction

In contrast to molecular fluids these days, ionic liquids (ILs) have attained widespread dimensions of applicability and versatility^1–6 through the ever-growing interest in their fascinating properties.^7,8 There is an enormous possibility for fine-tuning these properties with a little molecular constitution variability.^7,9 In addition, ILs need to be explored for the unveiled aspects of protic nature.^8,10,11 In the realm of inherent nature and interactive behavior of fluids, even for many years before the advent of ILs, the common theories still need to be checked to see whether they are applicable. It is imperative to have insights on the physiochemical-molecular pattern through experimentation and/or theoretical calculations, dynamics,⁹ and predictions¹² to enhance their operational utility.

Benzylic compounds have spanned usage in day-to-day life in the forms of surface active compounds, cosmetics, preservatives, antiseptics, antimicrobial agents, corrosion inhibitors and so on for ages, yet ILs are found to be in lack of such a globally relevant moiety. Notwithstanding, the benzylic quats, the benzyl-appended quaternary ammonium molten designer salts, herein, can incorporate numerous ecofriendly and industrially relevant peculiarities that can be beautifully adorned through methylene/methyl impregnated in their structural constitution (anionic as well as cationic) from a chemical point of view. Such an appendage has predominately been a subject matter of imidazolium skeletons with inorganic anions revealing the fascinating physiochemical response of ILs so far.^13,14 It has also been found in some imidazolium and pyridinium ionic liquids that bearing benzyl appendages gives significant potential for use in the separation of carbon dioxide from combustion products on the grounds of membrane performance tests and CO₂ solubility measurements.¹⁵ Furthermore, the benzylic systems show an alluring “benzylic effect”, a marked increase in rates of S_N2 reactions in contrast to analogous alkyl derivatives, and find constant significance in organic synthesis, specifically as protective groups and pharmaceutical moieties. Benzyl-based ammonium compounds have been proven to be effective long term in large scale microbial eradication and control.^16,17 In addition, these serve as good surface active compounds. Ammonium-based ionic liquids have been shown as effective alternatives to the demands for volatile organic compounds (VOCs) as solvents, elevated temperatures and pressures, and toxic catalysts, in addition to their ease of preparation at a lower environmental and economic cost.¹⁸ In the same vein, carboxylate anionic chains of a longer size (ca. the range of our study) have shown a relatively reduced cytotoxicity.¹⁹ Furthermore, a combined effect of alkyl–aryl substituents on the aliphatic parent structures seems interesting to explore for the behavioral pattern of ILs.²⁰ A systematic unification of such a variation in molecular integrity, aided by some simple chemistry and statistical tools, phrased herein as molecular tools (described in the Experimental section), empowers us to switch to better alternatives even for working out the design of large scale industrial processes, which calls for accurate thermophysical data frequently in large volumes. This report illustrates our efforts in molecular design to visualize the thermophysical behavior of new benzyl-appended ionic liquids’ structural variants through an easy-to-choose molecular shuttle of –CH₂/–CH₃ both at the anionic and cationic ends.

To name a few, the key subjects of this study are the synthesis of a new family of 13 ILs employing a benzylic moiety via a green atom-economic protonation–deprotonation, a mix of non-destructive experimental characterizations (FT-NMR, FTIR, TOF MS ES+, densimetry, ultrasonics), measurements and evaluation of a number of fundamental derived properties (ρ, u, V_m, α, β_S, R, A, etc.) with correlations to structural features at the molecular level, and sub-classification of the family on the grounds of thermodynamic considerations at temperatures ranging from 293.15 to 343.15 K. In this context, the groups contributing to the thermophysical properties, the structural descriptors, are deduced and validated further with one of the ILs’ properties. Employing such an external test, the data determines the limit of working uncertainty in predictions of the molecular features of other ILs in a green way. The concept of a chemical middleman has been deduced in the perspective of the additivity principle (referred to as the fourth law of thermodynamics).²¹ Utilizing such tools, methodologies, and relevant quantities like ΔpK_a (the difference in the pK_a value for the acid and base determined in dilute aqueous solutions) in molecular tailoring, this study substantially raises questions on the proposed feasibility^8,10,22,23 of ILs’ macroscopic–microscopic behavior and allied phenomenology. Furthermore, it radically poses challenges²⁴ to the applicability of numerous theories for molecular fluids^25–28 to ILs, which need to be upgraded. In this regard, the present work establishes the following aspects: (i) the specific design of ILs showing a commonly seen variation in them, (ii) ILs featured in an analysis in the framework of Schaaffs’ collision factor theory of the speed of sound, u, the Newton–Laplace equation for isentropic compressibility, β_S, Rao’s relation for molecular sound velocity, R, and Wada’s model for molecular compressibility, A, over molecular fluids, and their variation with temperature, and (iii) the quest for a middleman in molecular modeling accounting for ILs’ inherent behavior to these quantities in terms of structural descriptors, and in light of Jacobson’s relation for intermolecular free length, L_f, the contributions to molar or molecular volume, V_m, etc.

Results and discussion

The molecular puzzle

This explorative excursion begins with inspiration from nature itself wherein a benzylic skeleton is ubiquitous. It is attempted to bring it into designing aspects of the molecular puzzle through tailoring²⁹ in the form of a new edition to the outlook to the ILs where it is scarce. Equipped with molecular tools, it proceeds through a feasible synthesis^29–31 and other attempts made in the Experimental section, and thorough investigation of the physiochemical behavior¹² of all the variants, followed by logical molecular tailoring (fragmentation while employing the group contribution method, and reunion while employing the validation approach). The evolutionary history of benzylic quats and the basics of our study in the context of the molecular puzzle have been well depicted through a flowchart in Fig. 1 that presents unwinding it through logical breaks and links thenceforth. During the course of progress it undergoes a multitude of analyses, with justifying and/or comparable support from the available literature. Meanwhile, it aids the analysis of applicability of the currently prevailed theories and conceptions on molecular fluids^25–28 to ILs, that will get depicted in the molecular design³² of the puzzle.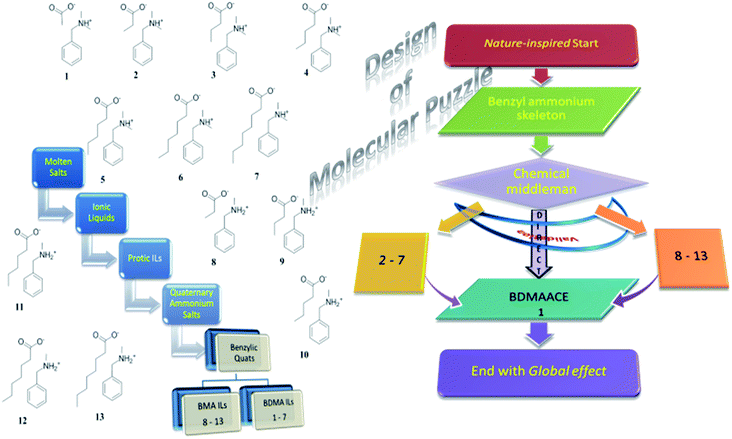

Fig. 1 Flowchart showing a schematic representation of the basics of our study and an evolutionary tree showing the origin of benzylic quats.

Densimetry

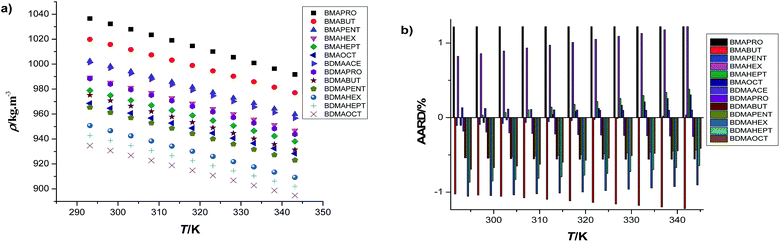
This could be the first tool to be considered in the process of molecular tailoring of the puzzle to find the probable middleman deciding the design. It can be visualized from Fig. 2 and Table S2† that BMAPRO is the densest and BDMAOCT is the lightest among all the ILs under study. Amidst the ILs of the same cation family, there is a prominent effect of anionic alkyl chain-length and our results agree with the fact that long alkyl chains lower the density, ρ, of the corresponding ILs.³³ These follow the order BDMAOCT < BDMAHEPT < BDMAHEX < BDMAPENT < BDMABUT < BDMAPRO and BMAOCT < BMAHEPT < BMAHEX < BMAPENT < BMABUT < BMAPRO as depicted through lower molecular volumes, V_m, of the propionate salts in Table 1. Quantitatively, one –CH₂ incorporation changes the density by 4.68% amongst ILs in the propionate family rather than 3.52% in the octanoates under ambient conditions. As each IL is to be observed individually from the tabulated values, graphically presented as Fig. 2, the incorporation of –CH₂ groups lowers the density, only by 6.55%, in BMAOCT relative to BMAPRO whereas this result is 5.41% in BDMAOCT with respect to BDMAPRO at 298.15 K. Among the benzylic quats the magnitude of such a contribution for each –CH₂, as suggested from the group contribution technique through the least square regression procedure,^12,34 is 0.0289 nm³ for V_m which agrees quite well with that for alcohols (0.0280 nm³), n-paraffins (0.0267 nm³), n-amines (0.0272 nm³), and for several other ILs reported so far as depicted in the previous work from our group.¹¹

Fig. 2 Representation of experimental data showing the thermodynamic profile and agreement between experimental and correlated data (predicted data in the case of BDMAACE) at different temperatures and at atmospheric pressure.

Table 1 Various derived properties under consideration at 298.15 K and 0.1 MPa

Benzylic quats	Vmolar × 10^6 /m^3 mol^−1	α × 10^4 /K^−1	βS /TPa^−1	R	A
BMAPRO	188.37	8.43	413.42	2180.0	80.0
BMABUT	205.21	8.15	429.34	2366.0	86.7
BMAPENT	222.77	8.28	449.38	2556.5	93.5
BMAHEX	239.90	8.38	461.41	2747.3	100.3
BMAHEPT	256.79	8.11	471.04	2935.2	107.0
BMAOCT	274.02	8.24	481.64	3126.2	113.8
BDMAACE	195.00	8.91	501.75	2198.5	80.6
BDMAPRO	211.75	8.97	510.94	2385.3	87.3
BDMABUT	229.01	8.91	530.04	2569.7	93.9
BDMAPENT	245.85	8.70	537.32	2756.6	100.6
BDMAHEX	264.39	8.67	548.19	2962.2	107.9
BDMAHEPT	281.50	8.57	552.47	3153.9	114.7
BDMAOCT	298.95	8.50	555.71	3350.9	121.7

---

Comparatively, BMA-appended ILs are dense as suggested by their relatively lower V_m. The small size of BMA cations makes them able to be compactly entangled in contrast to the bulkier BDMAs and the availability of free space is being avoided, which further causes incompressibility expressible through the speed of sound, u, measurements. Literary comparison is not possible so far to account for such molecular variability; however, it is quite reasonable to look through these variants so as to formulate task-specific molecular design. Herein, it can be visualized from the structural constitution of both cations that in each case the –CH₃ introduction in place of hydrogen in the BMA cation causes a decrease in the density of BDMA, as reflected from the mean contribution of 0.1080 nm³ to V_m at 298.15 K, similar to the –CH₂ introduction on the anionic end. In this way, BDMAOCT has the lowest density as predicted from its structural peculiarities. Five more –CH₂ groups and a –CH₃ group in the structural identity of BMAPRO produces BDMAOCT with a tremendous increase in molecular volume that can be ascribed as a possible root cause of such a huge variation. Table 2 summarizes the mean contribution of the constituting groups of the investigated benzylic quats’ variants at ambient temperature and pressure. Overall it seems that the steric factor dominates over the density values for such a class of ILs in relation to both cationic and anionic variability. Extra free volume created by such bulkier groups results in a comparatively lower density being found. Moreover, the findings on the density profile are quite consistent to the ΔpK_a approach previously reported,^8,11 among the benzylic quats. The greater the ΔpK_a, the greater the density found amongst both BMA and BDMA ILs which signifies the strength of bonding between cationic and anionic counterparts. Such measurements and data compilation on physiochemical behavior can be useful to a restricted mass only, unless they are aided by analytical features on the obtained trends, which further demands thermodynamic and statistical tools for the shortcomings in logical reasoning and interpretation capabilities for a tremendous number of possible ILs.

Table 2 Constitutive properties of benzylic quats^a

Property	CH3	C6H5CH2NH^+	C6H5CH2NH2^+	CH3COO^−	CH2	%AARD	%ARD for BDMAACE
a AARD: average absolute relative deviation, ARD: absolute relative deviation.
Vm /nm^3	0.1080	0.0133	0.0816	0.0949	0.0289	0.13	0.29
R	287.5	1048.4	1140.9	555.5	195.0	0.34	0.89
A	25.2	5.1	22.8	24.9	6.8	0.13	0.19

---

Table 1 also presents the values for the coefficient of thermal expansion, α, at ambient temperature and pressure to have a further understanding of the role of temperature in the volumetric behavior of these fluids. It is customary to say that α values are lower for associated liquids like acids and alcohols. It is found that these features are more similar to conventional imidazolium-based ionic liquids than to common organic solvents. Such behavior can be ascribed partly to the presence of ionic bonds in their constitution at a molecular level. Since the densities decrease with temperature it is quite understandable that the α values are positive, increasing with temperature. As is customary, it reaches higher values as the temperature progresses but not at a very significant rate, hence only the values at ambient conditions are tabulated. The predominance of the effect can be easily understood through bond strength among the structural constituents of the ILs, which further raises the significance of the u measurements. At least at this point in time, the role of the temperature increment can be perceived through the rise in the average intermolecular separation at high kinetic energy levels. As the temperature of the liquid increases, the mean molecular distance also increases, resulting in a decreased u value, because at a given temperature it is inversely proportional to the ninth power of the mean distance between the molecules at that temperature in the liquid.²⁵

Ultrasonics

T. S. Khasanshin and T. B. Zykova proclaimed, “A promising method of drawing up tables of thermodynamic parameters for liquid is provided by using acoustic measurements as input data”.³⁵ With the same intention, in a similar fashion to that of density, the speed of sound data have been taken³⁴ with reasonable uncertainty and presented in Table S2,† following the order: BMA ILs > BDMA ILs. Apparently, alkyl chain elongation lowers the magnitude of u amidst the ILs of the same cation family, in accordance with the expansion of the spatial intermolecular void with respect to the inherent molecular steric constraints. However, this lies in contrast to the study by M. Povey et al.³⁴ where they claim that the end unit, adjacent chain, H-bonding effects, etc., which play a role in the magnitude of u in terms of molecular orientation, geometry and assembly, can make the effect of carbon chain growth insignificant and can lead to an inversion of the observed trends as is featured in the case of BDMAOCT. The study is made further subject to the influence of temperature as correlated through the quadratic equation in Table S2† and the corresponding parameters can be procured from Table S3 in the ESI.† Nevertheless, their high magnitude is accredited to the existing aromatic moiety as featured in the earlier reports.²⁵ The phenomenon can be easily understood through the conception of intermolecular free length, L_f, while the acoustic wave gets transmitted through the fluid, which further calls for the compressibility, β_S, or speed of sound data such that The lower the compressibility, the lower the intermolecular free length³⁶ expressed by Jacobson’s relation, as such, the greater the efficiency of the wave transmission, resulting in the greater speed of sound. According to W. Schaaffs’ collision factor theory³⁷ of the speed of sound in pure liquids, u is proportional to the product of the collision factor that is featured through the elasticity of the mutual molecular collisions, and the space filling factor of the molecules, which adds new insight to visualize the thermodynamic trends.

The chemical constitution in the molecular scaffold

Let us now look for the chemical constitution of the molecular scaffold. As mentioned above, the compilation of u data is quite relevant in plenty of ways that need to be elaborated in here. It is worthwhile to get any possible insight into the chemical constitution of the substance through the simple laws relating u, for instance, to molecular volume in liquids, so as to deduce M. R. Rao’s molecular sound velocity R = u^1/3M/ρ where all the terms have their usual meanings. It signifies the comparison of molecular volumes of two liquids at temperatures at which the acoustic velocity is the same. Notwithstanding, analogous to V_m, the constant R can be regarded to follow the same additivity being constitutive in nature in the structural aspects. It varies in the same manner as the number of carbon atoms or the molecular weight, unlike the variations in the ρ and u profiles mentioned above; however, it stays almost invariant with temperature alteration as described originally.²⁵ The observed trend is quite consistent with that of V_m as described above, being a constitutive property. The values are found to be higher than those for common liquids as studied so far, leading to an inference of these being associative at the molecular level due to the lower cohesive energy these possess, as is observed in the case of the constitution study on alcohols by G. W. Marks.³⁸ Relying on the R values of C, H, O and the double bond contributions reported from the examination of several homologous series of organic liquids in the original findings of Rao,²⁵ years ago before the advent of ILs, the value for N, the missing one, is deduced and its contribution is assigned to be −91.6. Henceforth, the contributions for the five candidates have been calculated and are listed in Table 2. The predictions were justified through the external test material BDMAACE revealing only 0.89% deviation relative to the value obtained from Rao’s relation mentioned above. To be frank about the predictive behavior of such proposals of the contribution, it does rely on the nature of the molecular constitution²⁶ that further aids our approach of validation through an external data set of the same family and gives essential clues about the constitutive behavior, the designing and modeling aspects of the solutions to the subject of our concern, the molecular puzzles, and recognizing the chemical middleman deciding such behaviors. The validated results and the estimated contributions of –CH₂and –CH₃, along with the rest of the other basic constituents of benzylic quats, are addressed in Table 2 along with the other constitutive properties under investigation. Such a table seems necessary due to the lack of u measurements being constitutive and predictive.

At this moment it is noteworthy to point out the constitutive behavior of the R values gathered here, and that these fluids constitute two homologous series as is obvious from the various properties under consideration, depending upon the constitutive behavior of the cation rather than the anion, such that R increases in every series with an increase in the molecular chain-length in an entirely different manner, as proposed^25,28 from the relation R = AM + B. Here, A and B are empirical constants²⁵ such that A is a general constant independent of the series (ca. 14 as originally proposed in the case of molecular fluids) and B is a characteristic constant for any one homologous series that varies considerably amidst the two. In this context, it is clearly demonstrated now that Rao’s work on molecular fluids is still applicable to ILs. In the same vein, it could be added that R is the constitutive property rather than u.

In common practice, u has so far been chiefly intended for rendering β_S. When the ultrasonic absorption of the acoustic waves is in so far as negligible, as is the case with the manufacturer’s design of the apparatus employed here, β_S can be deduced from these through the application of the familiar Newton–Laplace equation and is tabulated in Table 1. The work signifies the understanding of bond strength and incompressibility terms arising earlier in this report. As featured above in the discussion part of the density trends, the availability of extra free volume accounted for steric factors of the bulkier groups decreases not only the density but also causes an increase in the compressibility values, which gives a sense of the wide applicability of the Newton–Laplace relation here as well. It is reasonable to add here that the chain-length dependence of compressibility possesses much more significance over the density, since the latter can be regarded essentially as a geometrical packing phenomenon while the former constitutes two features: intramolecular, associated with the flexibility of the covalent bonding in the chain, and intermolecular, associated with the flexibilities of a variety of intermolecular interactions.³⁴ This justifies the inverse profile of the compressibility values with respect to those of the ρ and u data. Furthermore, higher β_S values of benzylic quats compared to those of the conventional imidazolium ionic liquids can be ascribed to more free volume generated through the constituent bulkier groups. This way, this study also brings molecular features³² into common understanding, and the variability profiles in our rigorous quest for the chemical middleman into solutions to the molecular puzzle.

Following the goal of understanding the molecular constitution of benzylic quats through thermodynamic perspectives, a further attempt has been made to deduce Wada’s molecular adiabatic compressibility, A, employing the bond contributions from his original piece of remarkable work on more than 120 liquids²⁷ so as to account for numerous factors e.g. the constitutive nature of R, was used by Wada as merely an approximation to A; temperature independency of the term ρβ_S^1/7 was appraised by Rao himself, and lower R values are often observed for associated liquids. Meanwhile, with the experimental ρ and u data A has also been calculated through Wada’s own relation A = M/(ρβ_S^1/7). Huge deviations are observed as illustrated in Table S4† among the values from the two modes applied, revealing that the contributions proposed for normal liquids fail to predict the behavior of ILs, raising the practical need to be redefined and established once again, thus proposed in Table 2. This sort of inconsistency in chemical constitutional behavior deduced on the grounds of the additivity principle might have arisen from the negligence of coulombic forces in such molecular fluids that stay predominant in ILs. The established derived properties (V_m, R and A) of BDMAACE and the values predicted through the group contribution approach are in good agreement, while validation is presented in Table 2.

This further elucidates that additivity for Wada’s quantity might not be the case for ILs, in broader perspectives, henceforth in a way demanding for reinvestigations and amendments to be made. In this manner the additivity principle thus exercised for bond contributions could not be accountable for non-covalent interactions amongst ionic liquid entities.

To sum up the attempts made so far in unwinding the web interwoven amongst the members of the family of benzylic quats in the form of a puzzle, a rigorous investigation through molecular tailoring was executed and connecting links were drawn out through the tools of thermodynamic physiochemical-molecular modeling and constitutive behavior, which is thoroughly sought out throughout. The five qualified candidates for the title of the chemical middleman were thereby analyzed in such terms and the candidates constituting a benzyl ammonium skeleton (two amongst the five) and the one possessing the carboxylate moiety, having been featured as the characteristic to all the variants with impractical physical significance to other sorts of ionic liquids, must have been eliminated out, leaving behind the versatile two which are potentially inter-assimilative. Only their candidatures get qualified in an obvious way to the embellishment for such a title, for these stayed as the basics in the molecular integrity and identity of ionic liquids in the benzylic quats’ numerous variants.

Experimental section

Information on the chemicals employed, source, purity and prior treatment, if any, are provided in Table S1,† while synthetic methodology, characterization techniques and the mode of experimentation were significantly described in our previous communication^11,39 and a schematic representation of the synthetic procedure is illustrated in Scheme 1.

Scheme 1 Schematic representation of the synthetic methodology adopted.

The structural elucidation of the ionic liquids is carried out as follows:

Benzylmethylammonium propionate (BMAPRO)

¹H NMR (500 MHz, CDCl₃): δ ppm 7.89 (broad, 1H) 7.38–7.29 (m, 5H), 3.97 (s, 2H), 2.42 (s, 3H), 2.21 (q, 2H), 1.07 (t, 3H); ¹³C NMR (500 MHz, CDCl₃): δ ppm 180.4 (C=O), 134.2, 129.0, 128.4 and 127.9 (benzene ring carbons), 52.9 (CH₂–N), 32.4, 29.4, and 9.9 (saturated carbons); QTOF MS ES+ (m/z): calculated for (C₈H₁₂N⁺) 122.0970, found 122.0966.

Benzylmethylammonium butanoate (BMABUT)

¹H NMR (400 MHz, CDCl₃): δ ppm 9.51 (broad, 2H, NH₂⁺), 7.34–7.28 (m, 5H, Ar CH), 3.87 (s, 2H, benzylic CH₂), 2.39 (s, 3H, N–CH₃), 2.15 (t, 2H, COCH₂), 1.57 (sextet, 2H, CH₂), 0.90 (t, 3H, CH₃); ¹³C NMR (400 MHz, CDCl₃): δ ppm 180.1 (C=O), 133.5, 129.7, 128.8 and 128.6 (benzene ring carbons), 52.7 (CH₂–N), 39.0, 32.3, 19.5 and 14.1 (saturated carbons); QTOF MS ES+ (m/z): calculated for (C₈H₁₂N⁺) 122.0970, found 122.0964.

Benzylmethylammonium pentanoate (BMAPENT)

¹H NMR (400 MHz, CDCl₃): δ ppm 9.09 (broad, 2H, NH₂⁺), 7.38–7.27 (m, 5H, Ar CH), 3.87 (s, 2H, benzylic CH₂), 2.41 (s, 3H, N–CH₃), 2.18 (t, 2H, COCH₂), 1.55 (qn, 2H, CH₂), 1.32 (sextet, 2H, CH₂), 0.89 (t, 3H, CH₃); ¹³C NMR (400 MHz, CDCl₃): δ ppm 180.2 (C=O), 134.0, 129.5, 128.9 and 128.5 (benzene ring carbons), 53.0 (CH₂–N), 36.7, 32.6, 28.3, 22.7, and 14.0 (saturated carbons); QTOF MS ES+ (m/z): calculated for (C₈H₁₂N⁺) 122.0970, found 122.0974.

Benzylmethylammonium hexanoate (BMAHEX)

¹H NMR (500 MHz, CDCl₃): δ ppm 7.37–7.26 (m, 5H), 6.27 (broad, 1H), 3.85 (s, 2H), 2.434 (s, 3H), 2.20 (t, 2H), 1.58 (qn, 2H), 1.33–1.28 (m, 4H), 0.89 (t, 3H); ¹³C NMR (500 MHz, CDCl₃): δ ppm 180.3 (C=O), 135.1, 129.6, 129.0 and 128.6 (benzene ring carbons), 53.7 (CH₂–N), 36.9, 32.2, 32.0, 25.9, 22.8 and 14.3 (saturated carbons); QTOF MS ES+ (m/z): calculated for (C₈H₁₂N⁺) 122.0970, found 122.0973.

Benzylmethylammonium heptanoate (BMAHEPT)

¹H NMR (400 MHz, CDCl₃): δ ppm 9.15 (broad, 2H, NH₂⁺), 7.39–7.28 (m, 5H, Ar CH), 3.89 (s, 2H, benzylic CH₂), 2.42 (s, 3H, N–CH₃), 2.19 (t, 2H, COCH₂), 1.57 (qn, 2H, CH₂), 1.36–1.24 (m, 6H, CH₂), 0.89 (t, 3H, CH₃); ¹³C NMR (400 MHz, CDCl₃): δ ppm 180.1 (C=O), 133.6, 129.7, 128.9 and 128.7 (benzene ring carbons), 52.9 (CH₂–N), 36.7, 32.4, 31.8, 25.8, 22.6, 14.1 (saturated carbons); QTOF MS ES+ (m/z): calculated for (C₈H₁₂N⁺) 122.0970, found 122.0967.

Benzylmethylammonium octanoate (BMAOCT)

¹H NMR (400 MHz, CDCl₃): δ ppm 8.16 (broad, 2H, NH₂⁺), 7.39–7.28 (m, 5H, Ar CH), 3.88 (s, 2H, benzylic CH₂), 2.43 (s, 3H, N–CH₃), 2.20 (t, 2H, COCH₂), 1.57 (qn, 2H, CH₂), 1.31–1.27 (m, 8H, CH₂), 0.89 (t, 3H, CH₃); ¹³C NMR (400 MHz, CDCl₃): δ ppm 180.1 (C=O), 134.3, 129.5, 128.9 and 128.5 (benzene ring carbons), 53.2 (CH₂–N), 36.8, 31.9, 29.6, 29.3, 26.1, 22.8 and 14.2 (saturated carbons); QTOF MS ES+ (m/z): calculated for (C₈H₁₂N⁺) 122.0970, found 122.0973.

Benzyldimethylammonium acetate (BDMAACE)

¹H NMR (500 MHz, CDCl₃): δ ppm 7.37–7.30 (m, 5H), 6.99 (broad, 1H), 3.72 (s, 2H), 2.39 (s, 6H), 2.03 (s, 3H); ¹³C NMR (500 MHz, CDCl₃): δ ppm 176.2 (C=O), 134.5, 130.2, 128.7 and 128.3 (benzene ring carbons), 62.4 (CH₂–N), 43.3, and 22.2 (saturated carbons); QTOF MS ES+ (m/z): calculated for (C₉H₁₄N⁺) 136.1126, found 136.1128.

Benzyldimethylammonium propionate (BDMAPRO)

¹H NMR (500 MHz, CDCl₃): δ ppm 7.37–7.30 (m, 5H), 6.84 (broad, 1H) 3.71 (s, 2H), 2.38 (s, 6H), 2.32 (q, 2H), 1.14 (t, 3H); ¹³C NMR (500 MHz, CDCl₃): δ ppm 179.6 (C=O), 135.03, 130.4, 128.8 and 128.4 (benzene ring carbons), 62.7 (CH₂–N), 43.6, 28.8 and 9.9 (saturated carbons); QTOF MS ES+ (m/z): calculated for (C₉H₁₄N⁺) 136.1126, found 136.1127.

Benzyldimethylammonium butanoate (BDMABUT)

¹H NMR (500 MHz, CDCl₃): δ ppm 8.16 (broad, 1H, NH⁺), 7.34 (m, 5H, Ar CH), 3.73 (s, 2H, benzylic CH₂), 2.39 (s, 6H, N–CH₃), 2.27 (t, 2H, COCH₂), 1.65 (sextet, 2H, CH₂), 0.96 (t, 3H, CH₃); ¹³C NMR (500 MHz, CDCl₃): δ ppm 178.7 (C=O), 134.6, 130.3, 128.7 and 128.3 (benzene ring carbons), 62.4 (CH₂–N), 43.3, 37.6, 19.0, and 14.0 (saturated carbons); QTOF MS ES+ (m/z): calculated for (C₉H₁₄N⁺) 136.1126, found 136.1129.

Benzyldimethylammonium pentanoate (BDMAPENT)

¹H NMR (500 MHz, CDCl₃): δ ppm 8.52 (broad, 1H, NH⁺), 7.34 (m, 5H, Ar CH), 3.76 (s, 2H, benzylic CH₂), 2.41 (s, 6H, N–CH₃), 2.28 (t, 2H, COCH₂), 1.61 (qn, 2H, CH₂), 1.36 (sextet, 2H, CH₂), 0.91 (t, 3H, CH₃); ¹³C NMR (500 MHz, CDCl₃): δ ppm 179.0 (C=O), 134.0, 130.4, 128.7 and 128.5 (benzene ring carbons), 62.2 (CH₂–N), 43.1, 35.3, 27.7, 22.6, and 14.0 (saturated carbons); QTOF MS ES+ (m/z): calculated for (C₉H₁₄N⁺) 136.1126, found 136.1126.

Benzyldimethylammonium hexanoate (BDMAHEX)

¹H NMR (500 MHz, CDCl₃): δ ppm 7.35–7.28 (m, 5H), 6.47 (broad, 1H), 3.66 (s, 2H), 2.35 (s, 6H), 2.28 (t, 2H), 1.63 (qn, 2H), 1.33–1.30 (m, 4H), 0.89 (t, 3H); ¹³C NMR (500 MHz, CDCl₃): δ ppm 179.6 (C=O), 135.0, 130.4, 128.8 and 128.4 (benzene ring carbons), 63.2 (CH₂–N), 44.1, 35.9, 32.1, 25.7, 23.0 and 14.4 (saturated carbons); QTOF MS ES+ (m/z): calculated for (C₉H₁₄N⁺) 136.1126, found 136.1128.

Benzyldimethylammonium heptanoate (BDMAHEPT)

¹H NMR (400 MHz, CDCl₃): δ ppm 10.39 (broad, 1H, NH⁺), 7.37–7.30 (m, 5H, Ar CH), 3.73 (s, 2H, benzylic CH₂), 2.39 (s, 6H, N–CH₃), 2.29 (t, 2H, COCH₂), 1.62 (qn, 2H, CH₂), 1.37–1.26 (m, 6H, CH₂), 0.88 (t, 3H, CH₃); ¹³C NMR (400 MHz, CDCl₃): δ ppm 178.9 (C=O), 130.3, 128.7, 128.3 (benzene ring carbons), 62.4 (CH₂–N), 43.35, 35.6, 31.7, 29.2, 25.6, 22.7, 14.2 (saturated carbons); QTOF MS ES+ (m/z): calculated for (C₉H₁₄N⁺) 136.1126, found 136.1131.

Benzyldimethylammonium octanoate (BDMAOCT)

¹H NMR (400 MHz, CDCl₃): δ ppm 11.14 (broad, 1H, NH⁺), 7.38–7.28 (m, 5H, Ar CH), 3.72 (s, 2H, benzylic CH₂), 2.38 (s, 6H, N–CH₃), 2.21 (t, 2H, COCH₂), 1.62 (qn, 2H, CH₂), 1.31–1.27 (m, 8H, CH₂), 0.88 (t, 3H, CH₃); ¹³C NMR (400 MHz, CDCl₃): δ ppm 178.9 (C=O), 134.6, 130.2, 128.7 and 128.3 (benzene ring carbons), 62.4 (CH₂–N), 43.3, 31.9, 29.5, 29.2, 25.7, 22.7 and 14.2 (saturated carbons); QTOF MS ES+ (m/z): calculated for (C₉H₁₄N⁺) 136.1126, found 136.1127.

All IR graphs show that the broad band appeared around 3400 cm⁻¹, exhibiting the characteristic ammonium peak and O–H stretching vibration, N–H plane bending vibrations and an aromatic C–C stretch around 1400 cm⁻¹, a C–N stretch for an aliphatic amine around 1220 cm⁻¹ and carbonyl stretching around 1700 cm⁻¹.

Moisture content was analyzed each time before and after use through the application of the well-known Karl Fischer coulometer technique and was found to be <0.2%. Sampling was done thrice corresponding to each lot synthesized and the measured data average is tabulated in Table S2.† Though the methodologies adopted are conventional, these have both basic and applied perspectives in the ever-expanding and flourishing domains of industrial, academic and R&D infrastructure. To take into account such broad aspects with full sincerity, high precision sophisticated world-class instruments are employed, and accuracy and purity have been given enough significance at each stage of experimentation. The thermodynamic profile with respect to molecular architecture is defined within reasonable uncertainty and justified adequately through a variety of tools like predictions, correlations, estimations, validations, comparisons and assimilation to the existing trends, and models and theories to present the clear-cut description of the modeling aspects of the application-specific new variants.

Furthermore, a blend of fundamental derived properties is assessed through empirical and semi-empirical relations. The external test material from the same family employed here for validation of the thermodynamic profile of the system under consideration not only validates the approach of group contribution,¹² but also presents the inherent trend explored with reasonable success and gives us the clues for the probable middleman in the additivity principle. Attempts are made, in addition, to execute the assimilation with existing models/theories for general fluid systems.

Thermodynamic insights and the group contribution approach

To get insights into the effect of temperature on volumetric properties, ρ and u are measured as a function of temperature and presented in Table S2.† Δρ is most pronounced in the case of BDMAPRO and the value of ρ decreases 4.52% at 343.15 K as compared to that at 293.15 K, and our results are further upheld by the fact that there exists an inverse relation between temperature and density for liquids, that is herein represented with a quadratic empirical correlation. Table S3† lists the best fit parameters for the investigated benzylic quats that are made subject to further distribution among five structural descriptors without any special weighting. The statistics of these correlations and predictions for error analysis are shown in Fig. 2. The study covers a 894.683 to 1036.587 kg m⁻³ density range. The higher density as compared to other conventional liquids can be assigned to π–π stacking of aromatic rings,³³ only characteristic to these benzylic quats. The predictions are justified through the external test material BDMAACE. Such predictive behaviors or contributions are characteristic to a constitutive molecular scaffold that raises the necessity of validation. With the same intentions in mind, an external data set of the same family was employed to our working data set, segregated out from the designing and modeling aspects, and to our delight the deviations are within reasonable limits, which makes us familiar with an array of qualified candidates for the chemical middleman deciding such behaviors. The validated results and the estimated contributions of such candidates are addressed in Table 2 along with the other constitutive properties under investigation compiled further to aid with the solutions of the molecular puzzle woven in the family of benzylic quats. Now an analysis is needed for recognizing the odd one out that itself demands a relative weighting of the various candidates to the properties for confirming the characteristics of the middleman. Such an exploration raises the significance of our research enterprise for thermodynamic profiling at a wide range of state variables, say temperature herein. This is further boosted with ultrasonic treatment of the new variants.

The relative relevance of the approaches adopted in molecular tailoring for finding the chemical middleman in the molecular puzzle can be summed up in hierarchy as:

Synthesis → structural elucidation → property measurements and thermophysical assessment → empirical derivations → correlations–predictions–estimations → analysis and conceptualization → statistics and molecular modeling → validation and comparison → applicability in the process and product design.

Conclusions and prospects

A new family of benzyl-appended ammonium ionic liquids has been synthesized. Numerous methodologies were employed for molecular structure confirmation and their physiochemical behavior over a wide temperature range. Molecular volume, V_m, the coefficient of thermal expansion, α, the adiabatic compression coefficient, β_S, and intermolecular free length, L_f, have been derived and the inherent nature of the fluids has been deduced as associative. Significant insights have been drawn in the wide applicability of the Newton–Laplace relation. Semi-empirical Rao’s relation for molecular sound velocity, R, is employed to estimate the constitutive peculiarities at the microscopic level through the application of macroscopic properties like density, ρ, and the speed of sound, u, and the missing atomic contribution for nitrogen is propounded. The class is found to be segregated into two groups, depending upon the cationic integration. Wada’s model for liquids has been found to be inconsistent for ionic liquids, at least for these benzylic quats, and was thus reformulated. Meanwhile, a number of properties were also parameterized into five forms using twelve of the ILs under investigation, whereas the thirteenth one was treated as an external test substance on validation and the success is achieved within the limits of experimental error in both the cases of correlations and predictions. On thermodynamic grounds, it is demonstrated both qualitatively and quantitatively how a small group like –CH₂/–CH₃ behaves as the chemical middleman deciding both the micro and macroscopic properties and provides the essential justification to the title of this report. At last, the theoretical background in terms of electronic behavior of various intra and intermolecular factors related to ionic charge, dipole moment and polarizability ought to be explored in association to such thorough experimental investigations and phenomenology, yet the study seems fruitful to answer the molecular puzzle of structure to property variability and vice versa with reasonable success, and lays down a new foundation for a voyage on intriguing thoughts with molecular tools. Comparative literary accounts are placed to compensate for the missing data. Such rigorous attempts in solving the molecular puzzle via a middleman can be useful in task-specific applications through accessing ILs’ potential structural variability as desired or demanded.

The study has formulated several macroscopic properties reflecting the strengths of microscopic intra and intermolecular forces amongst a new family of ILs and their further classification. Moreover, it has employed non-destructive high precision volumetry, defined new variants’ thermodynamic profile, investigated structure–property coupling and estimated constitutive behavior without any harm to the environment. In this fashion, key-design in molecular architecture relative to physiochemical behavior can be unlocked and revealed through tailoring, herein the molecular shuttle of –CH₂/–CH₃ in a green way and a hypothesis for the chemical middleman have been propounded in the additivity phenomenon.

Acknowledgements

Authors are thankful to the Council of Scientific and Industrial Research (CSIR), India, the Department of Science and Technology (DST), India, and IIT Madras for their financial support through grant numbers 01(2525)/11/EMR-II, SR/FT/CS-45/2011 and CHY/10-11/523/NFSC/RAME, respectively. Authors acknowledge Dasthaiah Keshapolla for the help in the synthesis of a few ILs.

References

1. N. V. Plechkova and K. R. Seddon, Chem. Soc. Rev., 2008, 37, 123–150.
2. E. F. Borra, O. Seddiki, R. Angel, D. Eisenstein, P. Hickson, K. R. Seddon and S. P. Worden, Nature, 2007, 447, 979–981.
3. R. A. Sheldon, Green Chem., 2005, 7, 267–278.
4. J. Brennecke and E. Maginn, AIChE J., 2001, 47, 2384–2389.
5. A. Kumar and P. Venkatesu, Chem. Rev., 2012, 112, 4283–4307.
6. A. D. Sawant, D. G. Raut, N. B. Darvatkar, U. V. Desai and M. M. Salunkhe, Catal. Commun., 2010, 12, 273–276.
7. H. Tokuda, K. Hayamizu, K. Ishii, M. A. B. H. Susan and M. Watanabe, J. Phys. Chem. B, 2005, 109, 6103–6110.
8. M. Yoshizawa, W. Xu and C. A. Angell, J. Am. Chem. Soc., 2003, 125, 15411–15419.
9. C. Chiappe, A. Sanzone, D. Mendola, F. Castiglione, A. Famulari, G. Raos and A. Mele, J. Phys. Chem. B, 2013, 117, 668–676.
10. H. Ohno and M. Yoshizawa, Solid State Ionics, 2002, 154–155, 303–309.
11. P. Chhotaray and R. L. Gardas, J. Chem. Thermodyn., 2014, 72, 117–124.
12. J. A. P. Coutinho and R. L. Gardas, in Ionic Liquids: From Knowledge to Application, ed. N. V. Plechkova, R. D. Rogers and K. R. Seddon, American Chemical Society, 2009, vol. 1030, pp. 385–401.
13. F. J. Deive, M. A. Rivas and A. Rodríguez, J. Chem. Thermodyn., 2011, 43, 487–491.
14. R. Tao, G. Tamas, L. Xue, S. L. Simon and E. L. Quitevis, J. Chem. Eng. Data, 2014, 59, 2717–2724.
15. S. M. Mahurin, T. Dai, J. S. Yeary, H. Luo and S. Dai, Ind. Eng. Chem. Res., 2011, 50, 14061–14069.
16. G. Kaur, A. K. Mandal, M. C. Nihlani and B. Lal, Int. Biodeterior. Biodegrad., 2009, 63, 151–155.
17. M. Lavania, P. M. Sarma, A. K. Mandal, S. Cheema and B. Lai, J. Environ. Sci., 2011, 23, 1394–1402.
18. C. Wang, L. Guo, H. Li, Y. Wang, J. Weng and L. Wu, Green Chem., 2006, 8, 603.
19. N. Muhammad, M. I. Hossain, Z. Man, M. El-Harbawi, M. A. Bustam, Y. A. Noaman, N. B. Mohamed Alitheen, M. K. Ng, G. Hefter and C.-Y. Yin, J. Chem. Eng. Data, 2012, 57, 2191–2196.
20. S. Ahrens, A. Peritz and T. Strassner, Angew. Chem., Int. Ed., 2009, 48, 7908–7910.
21. K. Dill, J. Biol. Chem., 1997, 272, 701–704.
22. C. A. Angell, Science, 1995, 267, 1924–1935.
23. T. Welton, Chem. Rev., 1999, 99, 2071–2084.
24. M. Armand, F. Endres, D. R. MacFarlane, H. Ohno and B. Scrosati, Nat. Mater., 2009, 8, 621–629.
25. M. R. Rao, J. Chem. Phys., 1941, 9, 682–685.
26. R. T. Lagemann, J. Chem. Phys., 1942, 10, 759.
27. Y. Wada, J. Phys. Soc. Jpn., 1949, 4, 280–283.
28. S. Parthasarathy and N. Bakhshi, J. Phys. Chem., 1953, 57, 453–454.
29. M. Semsarilar and S. Perrier, Nat. Chem., 2010, 2, 811–820.
30. B. Horton, Nature, 1999, 400, 797–799.
31. J. H. Clark, Nat. Chem., 2009, 1, 12–13.
32. H. Weingärtner, Angew. Chem., Int. Ed., 2008, 47, 654–670.
33. J. Kagimoto, S. Taguchi, K. Fukumoto and H. Ohno, J. Mol. Liq., 2010, 153, 133–138.
34. M. Povey, Z. Stec, S. Hindle, J. Kennedy and R. Taylor, Ultrasonics, 2005, 43, 219–226.
35. T. S. Khasanshin and T. B. Zykova, J. Eng. Phys., 1984, 46, 399–405.
36. B. Jacobson, Acta Chem. Scand., 1952, 1485–1498.
37. W. Schaaffs, Molecular Acoustics, Springer-Verlag, Berlin, Heidelberg, 1967, vol. 5.
38. G. W. Marks, J. Acoust. Soc. Am., 1967, 41, 103–117.
39. D. Keshapolla, V. Singh, A. Gupta and R. L. Gardas, Fluid Phase Equilib., 2015, 385, 92–104.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra02391b

---