DOI:
10.1039/C5RA01964H
(Paper)
RSC Adv., 2015,
5, 36779-36786
Theoretical prediction of structural stability, electronic and elastic properties of ZrSi2 under pressure
Received
31st January 2015
, Accepted 15th April 2015
First published on 15th April 2015
Abstract
Structural, elastic, electronic and thermodynamic properties of ZrSi2 have been investigated by means of first-principles plane wave pseudopotential calculations combined with the quasi-harmonic Debye model. We find that the orthorhombic base-centered lattice structure (C49) ZrSi2 is mechanically stable up to 80 GPa according to the elastic stability criteria, and there is a transition from brittle to ductile nature at about 56.5 GPa. The calculated elastic anisotropy factors suggest that ZrSi2 is anisotropic and the degree increases with pressure. In addition, the bonding characteristics are discussed by analyzing the energy band structure, charge density distribution and Mulliken populations. The pressure and temperature dependences of the bulk modulus, specific heat, Debye temperature and thermal expansion coefficient are also discussed through the quasiharmonic Debye model.
I Introduction
Transition metal silicides have been widely used in medical, aerospace, electronic and many other fields because of their unique properties.1–4 TiSi2 in the C54 structure (face-centered orthorhombic) is not only important in integrated circuit manufacturing by serving as a low resistance contact to metal-oxide-semiconductor field effect transistors such as sub-100 nm gate MOSFET devices5–11 because of its fairly low resistivity (13–20 μΩ cm), but also attracts great attention for applications in very large scale integration (VLSI) technology due to its unique properties such as strong adhesion with silicon substrates, good thermal stability, and high corrosion resistance. Interestingly, TiSi2 has a metastable phase with a four times higher resistivity.12 The metastable phase appears at temperatures around 450–600 °C (ref. 8 and 13) with an orthorhombic base-centered lattice structure (C49 type). Zirconium locates in the same group (IVa) in the periodic table as Ti, as the counterpart, ZrSi2 are naturally expected to have similar physical and chemical characteristics with TiSi2. ZrSi2 formed by thin film reaction with Zr deposited on silicon also exhibits a relatively low resistivity (35–40 μΩ cm), high-creep strength, and high thermal stability.14-21 Additionally, one important advantage of ZrSi2 compared with TiSi2 is its phase stability within the C49 structure.22,23
ZrSi2 as a member of the Zr–Si binary alloys, in addition to being applied in VLSI,24 has also been used as an alternative additive to fabricate SiC fiber/ZrB2 matrix composite. It can improve the sinter ability as well as increase the oxidation resistance of ZrB2 ceramics.25,26
Lately, strain is being widely used to tailor physical properties of a material, namely strain engineering.27 In this report, based on the consideration of the application of strain engineering in semiconductor manufacturing to enhance device performance28–30 and the use of various strain engineering techniques has been reported by many prominent microprocessor manufactures including AMD, IBM, and Intel, we calculated the electronic and elastic properties of ZrSi2 under pressures by first principles, the data will provide reference for the application of the ZrSi2 on the strain engineering. In addition, we have also obtained the thermodynamic data of this compound such as the isothermal bulk modulus, specific heat, thermal expansion coefficient and Debye temperature under different temperatures and pressures through combining the quasi-harmonic Debye model.
This paper proceeds as follows: the details of the calculation method and theoretical model are described in Sec. II, followed by the calculated results and analysis in Sec. III. Conclusions are summarized in Sec. IV.
II Method of calculation
In the calculation of this paper, the CASTEP code31 based on DFT32 was used to perform the simulations, the ultrasoft pseudopotential in the Vanderbilt form33 was used for electron–ion interaction and the exchange and correlation potential was treated by the generalized gradient approximation (GGA) in the scheme of Perdew–Burke–Ernzerhof (PBE).34 Zr (4s24p64d25s2) and Si (3s23p2) were served as the valence electron configurations. The cutoff energy of 400 eV and k-points of 7 × 2 × 7 in the irreducible Brillouin zone were used throughout. During the succedent calculations, the total stress tensor was reduced to the order of 0.02 GPa via the finite basis-set corrections, the maximum ionic Hellmann–Feynman force converged to a value of 0.01 eV Å−1 and the difference in total energy was minimized to below 5 × 10−6 eV per atom, The crystal geometry was optimized by using the BFGS algorithm35 under various hydrostatic pressures ranging from 0 to 80 GPa. The same parameters were adopted in the calculations of electronic structure and elastic properties.36
The elastic constants could be used to obtain credible elastic properties of inorganic compounds,37,38 which were calculated via the efficient stress–strain method at the optimized structures. The bulk modulus, Young's modulus, shear modulus, and Poisson's ratio were obtained by using the Voigt–Reuss–Hill approximation.39 The Debye temperature could be estimated from the elastic constants using the average sound velocity vm,40 and the thermodynamic properties of ZrSi2 under high temperatures and high pressures were investigated by the quasi-harmonic Debye model.41,42
III Results and discussion
3.1 The equilibrium lattice structure and equation of state
ZrSi2 crystallizes in an orthorhombic base-centered lattice structure (C49) with 12 atoms per conventional unit cell. Fig. 1 shows its total energy per formula unit as a function of volume and the inset is its conventional unit cell of crystal structure. The equilibrium lattice constants, bulk modulus and its pressure derivative are all listed in Table 1, together with available experimental results for comparison. The calculated lattice parameters are in well agreement with experiments, with the mismatch within 0.01%. Furthermore, the pressure dependence of the normalized parameters a/a0, b/b0, c/c0 and volume V/V0 for ZrSi2 is plotted in Fig. 2, where a0, b0, c0 and V0 are taken at T = 0 K and P = 0 GPa. It is clearly shown that compared with b/b0, c/c0 and a/a0 decrease much slower, that is to say ZrSi2 is much more compressible along the b-direction than along the a- and c-directions. This indicates that ZrSi2 exhibits an obvious elastic anisotropy. This reflects its anisotropic nature in bonding and structure of ZrSi2. Its structure can be seen as a distorted fcc lattice which has relatively short average lattice constant a and c and relatively long b. This feature implies relatively close packing within (0 1 0) plane (a–c plane) and relatively loose packing along the (0 1 0) direction (b axis) and hence short and strong Si–Si bonding and Zr–Si bonding within (0 1 0) plane and long and weak bonding along the b axis.
 |
| | Fig. 1 The total energy per formula unit as a function of volume for ZrSi2, and the conventional cell of crystal structure of ZrSi2. | |
Table 1 The calculated equilibrium lattice constants a0, b0, c0 (Å) and equilibrium volume V0 (Å3), bulk modulus B0 (GPa), and its pressure derivative B′0 for orthorhombic ZrSi2 at 0 K and 0 GPa
| |
a0 |
b0 |
c0 |
V0 |
B0 |
B′0 |
| Ref. 43. |
| This work |
3.706 |
14.735 |
3.672 |
200.5202 |
120.66 |
3.9493 |
| Experimentala |
3.6983 |
14.761 |
3.6646 |
200.0527 |
— |
— |
 |
| | Fig. 2 The normalized lattice parameters and volume as a function of pressure. | |
3.2 Elastic properties
In the elastic range, due to the symmetry of the crystal, there are nine independent components of the elastic tensor for ZrSi2, i.e., C11, C22, C33, C44, C55, C66, C12, C13 and C23. The pressure dependences of the elastic constants up to 80 GPa are illustrated in Fig. 3(a). It can be seen that all Cijs increase with pressure monotonically. Unfortunately, there are no experimental or theoretical data available for comparison. Therefore, our results could be a prediction for future studies. Furthermore, according to the well-known Born stability criteria,44 the independent elastic constants Cijs of mechanically stable orthorhombic crystals should satisfy the following mechanical stability criteria (formula (1)).45,46 In this report, the elastic constants of ZrSi2 satisfy the stability criteria up to 80 GPa, ensuring their respective mechanical stability under considered pressures, which is also confirmed by the calculated phonon dispersions at 80 GPa in Fig. 4 where no imaginary frequencies exist in the whole Brillouin zone.| | |
(C11 + C22 − 2C12) > 0, (C11 + C33 − 2C13) > 0, (C22 + C33 − 2C23) > 0, C11 + C22 + C33 + 2C12 + 2C13 + 2C23 > 0, C11 > 0, C22 > 0, C33 > 0, C44 > 0, C55 > 0, C66 > 0
| (1) |
 |
| | Fig. 3 Pressure dependence of the elastic constants Cij (a) and Debye temperature Θ (b) of ZrSi2 at 0 K. | |
 |
| | Fig. 4 Phonon dispersion curves for ZrSi2 at 80 GPa. | |
Debye temperature is an important parameter of compound, which is linked to many physical properties, such as specific heat, melting temperature, and elastic constants. In order to get further insights into the properties of ZrSi2, its Debye temperature Θ was calculated from the elastic constants by taking advantage of the relationship that Θ is proportional to the averaged sound velocity vm. At 0 K and 0 GPa, we obtained Θ = 570 K. The pressure dependence of Θ is presented in Fig. 3(b), where we can see that it increases monotonically with pressure rising. One can physically picture the Debye temperature as the temperature needed to activate all the phonon modes in a crystal. A crystal with a larger Debye temperature is expected to be stiffer. This is because the optical phonons have a higher frequency and therefore require greater energy to activate. Pressure typically enhances the interactions between atoms of a crystal and hence stiffers it, manifested by increased elastic moduli B and G. Therefore, pressure typically increases Debye temperature47,48 and this implies stronger interactions between atoms in the system.
An important relationship, which empirically links the plastic properties of materials with the elastic moduli of polycrystalline phases by considering the fact that the bulk modulus B stands for the resistance to fracture, and the shear modulus G stands for the resistance to plastic deformation, was proposed by Pugh.49,50 According to our calculated results, both B and G increase with pressure, as shown in the inset of Fig. 5. The value of B/G is 1.3 at zero pressure, illustrating that ZrSi2 is brittle at 0 GPa. This is because a low (high) B/G value is associated with brittleness (ductility), and the ductile and brittle materials are separated by the critical value (1.75). In this paper, the value of B/G increases monotonically with pressure (see Fig. 5) and arrives at 1.75 at 56.5 GPa, indicating a transformation from brittle to ductile nature, which also reflects the covalent-to-metallic bonding transformation of ZrSi2. Additionally, in consideration of the concept of chemical pressure that the addition of alloying elements often has similar and comparative effects as external pressure, our finding also provides possibility to the toughing of ZrSi2 by alloying which is of crucial importance for its practical applications. What's more, the present pressure related results are also of fundamental importance in geology.
 |
| | Fig. 5 The calculated B/G versus pressure for ZrSi2. Inset: bulk modulus B (GPa) and shear modulus G (GPa) derived from the Voigt–Reuss–Hill approximation as a function of pressure. | |
3.3 Elastic anisotropy
Elastic anisotropy is of momentous importance in the application of materials, which describes the behaviors of a crystal under external strain and provides fundamental information about the bonding characteristic between adjacent atomic planes and plays an important role in industrial applications.42,51 It is therefore necessary to estimate the elastic anisotropy of ZrSi2. The shear anisotropic factor provides a measure of the degree of anisotropy in the bonding between atoms in different planes. The shear anisotropy factor for the {100} shear planes between the 〈011〉 and 〈010〉 directions is defined as| |
 | (2) |
for the {010} shear planes between the 〈101〉 and 〈001〉 directions is| |
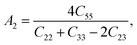 | (3) |
and for the {001} shear planes between the 〈110〉 and 〈010〉 directions is| |
 | (4) |
Using the relations mentioned above, the parameters about elastic anisotropy are calculated and presented in Table 2. The factors A1, A2, and A3 equal to 1.0 respectively show that ZrSi2 is isotropic, while any value smaller or larger than 1 indicates the amplitude of anisotropy of the crystal. At 0 GPa, the shear anisotropy results indicate that the elastic anisotropy for the {001} shear planes between the 〈110〉 and 〈010〉 directions is larger than that of the {100} shear planes between the 〈011〉 and 〈010〉 directions and the {010} shear planes between the 〈101〉 and 〈001〉 directions. Since ZrSi2 is orthorhombic, the shear anisotropy factors are not sufficient to fully describe its elastic anisotropy. Thus, the universal elastic anisotropy index AU is also invoked. It is defined by Ranganathan and Ostoja-Starzewski from the bulk modulus B and shear modulus G denoted by Voigt and Reuss approaches,52 as
| |
 | (5) |
Table 2 The shear anisotropy factors A1, A2, A3 and the universal elastic anisotropy index AU of ZrSi2 under pressure
| P |
A1 |
A2 |
A3 |
AU |
| 0 |
1.18 |
1.36 |
1.81 |
0.406 |
| 10 |
1.42 |
1.82 |
1.90 |
0.56 |
| 20 |
1.59 |
1.81 |
1.68 |
0.48 |
| 30 |
1.86 |
2.00 |
1.64 |
0.61 |
| 40 |
1.65 |
1.87 |
1.66 |
0.54 |
| 50 |
1.77 |
2.03 |
1.57 |
0.57 |
| 60 |
1.84 |
2.07 |
1.57 |
0.63 |
| 70 |
1.74 |
1.87 |
1.56 |
0.57 |
| 80 |
1.72 |
1.87 |
1.60 |
0.62 |
AU is zero for crystals which are elastically isotropic. The calculated AU of ZrSi2 under different pressures is also summarized in Table 2. The amplitude of a deviation from 0 is a measure of the degree of elastic anisotropy of the crystal. At 0 GPa, AU = 0.406, and it remained at about 0.6 with pressure increasing, which means that ZrSi2 is anisotropic.
3.4 Electronic properties
The band structure along high-symmetry lines of the Brillouin zone of ZrSi2 is plotted in Fig. 6. It can be seen that valence and conduction bands cross the Fermi level, which illustrates that ZrSi2 exhibits the metallic conductivity. The fact is also verified by the finite value of the DOS at EF displayed in Fig. 7. The site decomposed DOS in Fig. 7 shows the density of states with the Fermi level dominated by Zr 4d states, and even though considerable amount of Si 3s and 3p states are present in the occupied part of the DOS, their contribution at the Fermi level is very small. The lower part of the valence band ranging from −12.5 to −5 eV is dominated mainly by Si 3s and 3p states. The energy range from −5 to −2 eV is mainly derived from Zr 4p, 4d states and Si 3p states, and the upper part of the valence band in the energy range from −2 to 0 eV is dominated by a mixture of Zr 4d and Si 3p states.
 |
| | Fig. 6 Calculated energy band structure. | |
 |
| | Fig. 7 Partial density of states (PDOSs) of ZrSi2. The dashed lines represent the position of the Fermi level. | |
In order to get information about the pressure effects on the electronic properties of ZrSi2, we present its DOS at 10 GPa, 20 GPa, 30 GPa, 40 GPa, 50 GPa and 60 GPa respectively in Fig. 8. As shown, the DOS at Fermi level decreases with pressure, although the decreasing amplitude is not very significant, the tendency is distinct (2.916, 2.479, 2.199, 1.983, 1.785 and 1.641 for pressures from 10 GPa to 60 GPa according to Fig. 8). This phenomenon indicates that the stability of ZrSi2 gets stronger under pressure and the similar findings have been reported in earlier electronic structure studies on ordered intermetallic compounds and they yielded a definite correlation between N(EF) and their structural stability, which shows that low N(EF) is associated with higher stability.53–59
 |
| | Fig. 8 PDOS for ZrSi2 at different pressures. The dashed lines represent the position of the Fermi level. | |
Fig. 9 presents the calculated charge density distribution of ZrSi2 on the (100) plane. Obvious electron density accumulation can be seen between both neighboring Zr and Si atoms and Si and Si atoms, which is an indicative of a shared-electron feature and hence the covalent bonding nature of both Zr–Si and Si–Si bonding. Differences are also notable between the two types of bonding. Additionally, the electron accumulation is more significant in Si–Si bonding, indicating its more covalent nature than that of Zr–Si bonding. What's more, the charge distribution in Zr–Si bonding clearly concentrates toward the Si nuclei, in contrast to the homopolar distribution in the Si–Si bonding. Therefore, the Zr–Si bonding is polar covalent or in other words, exhibits an ionic nature. This is confirmed by the Mulliken population results as shown in Table 3, where we can see electron transfer from Zr to Si atoms. A large value of the overlap population indicates a high degree of covalency of the bond, and a low overlap close to zero indicates there is no significant interaction between the two atoms,60 thus the Si–Si bonding is more covalent compared with the other ones. Combining the Mulliken population and the previous analysis of band structure and DOS, we conclude that there are ionic bonding, covalent bonding and metallic bonding in the crystal.
 |
| | Fig. 9 Contour plot of the valence charge density in the (100) plane for ZrSi2. | |
Table 3 Atomic populations, bond populations and bond lengths of ZrSi2
| (a) Atomic populations |
| Species |
s |
p |
d |
Total |
Charge (e) |
| Si(1) |
1.4 |
2.73 |
— |
4.13 |
−0.13 |
| Si(2) |
1.44 |
2.56 |
— |
4 |
0 |
| Zr |
2.3 |
6.53 |
3.04 |
11.87 |
0.13 |
| (b) Bond populations and bond lengths |
| Bond |
Population |
Length (Å) |
| Si(1)–Si(1) |
0.46 |
2.456 |
| Si(2)–Si(2) |
0.27 |
2.715 |
| Si(1)–Zr |
0.33 |
2.821 |
| Si(2)–Zr |
0.36 |
2.849 |
| Si(2)–Zr |
0.35 |
2.890 |
3.5 Thermodynamic properties
The thermodynamic quantities of ZrSi2 at various temperatures and pressures can be obtained from the calculated E–V data at T = 0 and P = 0. Fig. 10 illustrates the pressure dependence of the normalized volume V/V0 and bulk modulus at specific temperature for ZrSi2, where V0 is the zero-pressure equilibrium volume. It can be seen that the V/V0 curve becomes steeper with temperature increasing, which implies that ZrSi2 is more easily compressed when temperature increases. Furthermore, it is found that the bulk modulus increases with pressure at a given temperature and decreases with temperature at a constant pressure, the latter being consistent with the trend of volume.
 |
| | Fig. 10 The calculated normalized volume V/V0 and bulk modulus of ZrSi2 as a function of pressure at temperatures 0, 200, 400, 600, 800, and 1000 K. | |
The heat capacity is not only beneficial to the understanding of vibrational properties of a substance but also is mandatory for many applications. The calculated heat capacity of ZrSi2 as a function of temperature at different pressures is demonstrated in Fig. 11. It is shown that the heat capacity CV fits T3 term in their low-temperatures and tends to zero when the temperature vanishes at the given 0, 10, 20, 30, 40, 50, 60 GPa. This is due to the harmonic approximations of the Debye model. At high temperature, CV does not depend much on temperature and converges to a constant value called Dulong–Petit limit. The heat capacity increases with temperature increasing at a given pressure, and decreases with applied pressure increasing at a constant temperature. It can also be seen from Fig. 11 that the temperature effect on CV is greater than the pressure effect.
 |
| | Fig. 11 Temperature dependence of the heat capacity at different pressures. | |
Fig. 12 shows the volume thermal expansion coefficient α as a function of temperature (pressure) at different pressures (temperatures). Because of the relationship between CV and  , and the weak dependence of the bulk modulus on temperature, the trend of the volume thermal expansion coefficient is similar to the heat capacity, i.e., it increases rapidly with temperature at low temperatures (α(T) ∼ T3) and gradually approaches a very slow linear increase at high temperatures (T > 300 K). As Fig. 12(a) shows, our results are in good agreement with available experimental data43 at relatively high temperatures in a range of 300–1000 K, and one can expect that if there were available experimental data at low temperatures, good agreement will be reached with our calculated results. Additionally, as seen from Fig. 12(b), at a given temperature, the thermal expansion coefficient decreases drastically under low pressures and the curve becomes flat with pressure increasing.
, and the weak dependence of the bulk modulus on temperature, the trend of the volume thermal expansion coefficient is similar to the heat capacity, i.e., it increases rapidly with temperature at low temperatures (α(T) ∼ T3) and gradually approaches a very slow linear increase at high temperatures (T > 300 K). As Fig. 12(a) shows, our results are in good agreement with available experimental data43 at relatively high temperatures in a range of 300–1000 K, and one can expect that if there were available experimental data at low temperatures, good agreement will be reached with our calculated results. Additionally, as seen from Fig. 12(b), at a given temperature, the thermal expansion coefficient decreases drastically under low pressures and the curve becomes flat with pressure increasing.
 |
| | Fig. 12 (a) Temperature dependence of the thermal expansion coefficient at different pressures. (b) Pressure dependence of the thermal expansion coefficient at various temperatures. | |
IV Conclusion
In conclusion, we have investigated the equilibrium structure, elastic, electronic and thermodynamic properties of orthorhombic C49 ZrSi2 by using first-principles plane wave pseudopotential calculations along with the quasiharmonic Debye model. The elastic constants under high pressure, elastic moduli under high pressure and high temperature, and the anisotropies of ZrSi2 are predicted. According to the elastic stability criteria, ZrSi2 is mechanically stable up to 80 GPa. In addition, the crystal exhibits brittle nature at 0 GPa and there is a transformation from brittle to ductile nature at P = 56.5 GPa. The calculated elastic anisotropy factors suggest that ZrSi2 is elastically anisotropic. Bonding characteristics are discussed by analyzing the partial density of states, charge density distribution and Mulliken populations. Note that there are ionic, covalent and metallic bonding components in the ZrSi2 crystal. Moreover, through the quasiharmonic Debye model, the pressure and temperature dependences of the bulk modulus, specific heat, Debye temperature and thermal expansion coefficient are discussed. The calculated thermal expansion coefficient α is in good agreement with available experimental data. The results show that pressure and temperature have remarkable effects on these thermodynamic properties. The present study provides detailed and systematic information for theoretical and experimental researches on ZrSi2, which is of fundamental importance for its industrial applications.
Acknowledgements
This work was supported by the NBRPC (grant 2013CB733000), NSFC (grants 51171160/51171163). J.Q would like to acknowledge support by Ratchadapisek Somphoch Endowment Fund for new Researcher of Chulalongkorn University, Ratchadaphisek somphoch Endowment Fund (2013), Chulalongkorn University (CU-56-805-FC), and Ratchadapisek Somphoch Endowment Fund, Chulalongkorn University, granted to the Surface Coatings Technology for Metals and Materials Research Unit (GRU 57-005-62-001).
References
- A. Cremasco, P. Andrade, R. Contieri, E. Lopes, C. Afonso and R. Caram, Mater. Des., 2011, 32, 2387–2390 CrossRef CAS PubMed
 .
. - Q. Guo, Y. Zhan, H. Mo and G. Zhang, Mater. Des., 2010, 31, 4842–4846 CrossRef CAS PubMed
 .
. - X. Huang, X. Zhang, Y. Zhu, S. Zhang, M. Ma and R. Liu, Comput. Mater. Sci., 2012, 62, 65–70 CrossRef CAS PubMed
 .
. - X. Chen, J. Guan, G. Sha, Z. Gao, C. T. Williams and C. Liang, RSC Adv., 2014, 4, 653–659 RSC
 .
. - S. Murarka, J. Vac. Sci. Technol., 1980, 17, 775–792 CrossRef CAS
 .
. - S. Murarka and D. Fraser, J. Appl. Phys., 1980, 1980, 51 Search PubMed
 .
. - F. d'Heurle, J. Electron. Mater., 1998, 27, 1138–1147 CrossRef
 .
. - H. Jeon, C. Sukow, J. Honeycutt, G. Rozgonyi and R. Nemanich, J. Appl. Phys., 1992, 71, 4269–4276 CrossRef CAS PubMed
 .
. - K. Maex, Mater. Sci. Eng., R, 1993, 11(vii), 153 Search PubMed
 .
. - V. Sisodia and S. Dhole, J. Mater. Sci.: Mater. Electron., 2013, 24, 3634–3639 CrossRef CAS PubMed
 .
. - L. Mattheiss and J. Hensel, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 7754 CrossRef CAS
 .
. - M. Ekman and V. Ozoliņš, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 4419 CrossRef CAS
 .
. - S.-P. Ju, T.-Y. Wu and S.-H. Liu, J. Appl. Phys., 2015, 117, 105103 CrossRef PubMed
 .
. - P. Perez, M. Lopez, J. A. Jiménez and P. Adeva, Intermetallics, 2000, 8, 1393–1398 CrossRef CAS
 .
. - K. Pomoni and J. Salmi, J. Phys. D: Appl. Phys., 1991, 24, 727 CrossRef CAS
 .
. - Y. Igarashi, T. Yamaji, S. Nishikawa and S. Ohno, Appl. Surf. Sci., 1990, 41, 282–285 CrossRef
 .
. - C. Sukow and R. Nemanich, J. Mater. Res., 1994, 9, 1214–1227 CrossRef CAS
 .
. - H. Jeon and S. Kim, Jpn. J. Appl. Phys., 1998, 37, 4747–4750 CrossRef CAS
 .
. - W. Liu, J. Liang, X. Zhou and X. Long, Mater. Lett., 2014, 122, 220–222 CrossRef CAS PubMed
 .
. - T. Nakano, Y. Omomoto, K. Hagihara and Y. Umakoshi, Scr. Mater., 2003, 48, 1307–1312 CrossRef CAS
 .
. - I.-J. Cho, K.-T. Park, S.-K. Lee, H. H. Nersisyan, Y.-S. Kim and J.-H. Lee, Chem. Eng. J., 2010, 165, 728–734 CrossRef CAS PubMed
 .
. - M. Setton and J. Van der Spiegel, J. Appl. Phys., 1991, 70, 193–197 CrossRef CAS PubMed
 .
. - J. Lin, W. Hsieh and L. Chen, J. Appl. Phys., 1996, 79, 9123–9128 CrossRef CAS PubMed
 .
. - T. Yamauchi, S. Zaima, K. Mizuno, H. Kitamura, Y. Koide and Y. Yasuda, Appl. Phys. Lett., 1990, 57, 1105–1107 CrossRef CAS PubMed
 .
. - H. Gesswein, A. Pfrengle, J. R. Binder and J. Hausselt, J. Therm. Anal. Calorim., 2008, 91, 517–523 CrossRef CAS PubMed
 .
. - S. Guo, T. Nishimura and Y. Kagawa, Int. J. Appl. Ceram. Technol., 2011, 8, 1425–1435 CrossRef CAS PubMed
 .
. - C. Li, C. Wang, F. Zhang, D. Ma, B. Wang and G. Wu, J. Phys. Chem. Solids, 2015, 78, 28–34 CrossRef CAS PubMed
 .
. - P. R. Chidambaram, C. Bowen, S. Chakravarthi, C. Machala and R. Wise, IEEE Trans. Electron Devices, 2006, 53, 944–964 CrossRef CAS
 .
. - V. Chan, K. Rim, M. Ieong, S. Yang, R. Malik, Y. W. Teh, M. Yang and Q. Q. Ouyang, Strain for CMOS performance improvement, 2005 Search PubMed
 .
. - D. A. Antoniadis, I. Aberg, C. Ni Chleirigh, O. M. Nayfeh, A. Khakifirooz and J. L. Hoyt, IBM J. Res. Dev., 2006, 50, 363–376 CrossRef CAS
 .
. - M. Segall, P. J. Lindan, M. Probert, C. Pickard, P. Hasnip, S. Clark and M. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717 CrossRef CAS
 .
. - R. G. Parr and W. Yang, Density-functional theory of atoms and molecules, Oxford university press, 1989 Search PubMed
 .
. - D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892 CrossRef
 .
. - J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS
 .
. - B. G. Pfrommer, M. Côté, S. G. Louie and M. L. Cohen, J. Comput. Phys., 1997, 131, 233–240 CrossRef CAS
 .
. - X.-L. Yuan, D.-Q. Wei, X.-R. Chen, Q.-M. Zhang and Z.-Z. Gong, J. Alloys Compd., 2011, 509, 769–774 CrossRef CAS PubMed
 .
. - X. Zhang, Z. Chen, C. Fan, M. Ma, Q. Jing and R. Liu, Phys. Status Solidi RRL, 2009, 3, 299–301 CrossRef CAS PubMed
 .
. - X. Zhang, L. Chen, M. Ma, Y. Zhu, S. Zhang and R. Liu, J. Appl. Phys., 2011, 109, 113523 CrossRef PubMed
 .
. - R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349 CrossRef
 .
. - O. L. Anderson, J. Phys. Chem. Solids, 1963, 24, 909–917 CrossRef CAS
 .
. - M. Blanco, E. Francisco and V. Luana, Comput. Phys. Commun., 2004, 158, 57–72 CrossRef CAS PubMed
 .
. - X. Zhang, J. Qin, J. Ning, X. Sun, X. Li, M. Ma and R. Liu, J. Appl. Phys., 2013, 114, 183517 CrossRef PubMed
 .
. - I. Engström and B. Lönnberg, J. Appl. Phys., 1988, 63, 4476–4484 CrossRef PubMed
 .
. - M. Born, On the stability of crystal lattices I, 1940 Search PubMed
 .
. - P. Chen, D.-L. Li, J.-X. Yi, L. Wen, B.-Y. Tang, L.-M. Peng and W.-J. Ding, Solid State Sci., 2009, 11, 2156–2161 CrossRef CAS PubMed
 .
. - X. Zhang, J. Qin, X. Sun, Y. Xue, M. Ma and R. Liu, Phys. Chem. Chem. Phys., 2013, 15, 20894–20899 RSC
 .
. - Y. Ciftci, K. Colakoglu, E. Deligoz and H. Ozisik, Mater. Chem. Phys., 2008, 108, 120–123 CrossRef CAS PubMed
 .
. - D. Connétable and O. Thomas, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 094101 CrossRef
 .
. - S. Pugh, Philos. Mag., 1954, 45, 823–843 CrossRef CAS
 .
. - Y. Pan, Y. Lin, M. Wen and Q. Meng, RSC Adv., 2014, 4, 63891–63896 RSC
 .
. - B. Karki, L. Stixrude, S. Clark, M. Warren, G. Ackland and J. Crain, Am. Mineral., 1997, 82, 51–60 CAS
 .
. - S. I. Ranganathan and M. Ostoja-Starzewski, Phys. Rev. Lett., 2008, 101, 055504 CrossRef
 .
. - Y. Imai, M. Mukaida and T. Tsunoda, Intermetallics, 2000, 8, 381–390 CrossRef CAS
 .
. - P. Ravindran and R. Asokamani, Bull. Mater. Sci., 1997, 20, 613–622 CrossRef CAS
 .
. - T. Hong and A. Freeman, J. Mater. Res., 1991, 6, 330–338 CrossRef CAS
 .
. - R. Kuentzler and R. M. Waterstrat, Solid State Commun., 1988, 68, 85–91 CrossRef CAS
 .
. - R. Kuentzler and R. M. Waterstrat, Solid State Commun., 1985, 54, 517–524 CrossRef CAS
 .
. - J.-H. Xu and A. Freeman, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 12553 CrossRef CAS
 .
. - J.-H. Xu, T. Oguchi and A. Freeman, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 36, 4186 CrossRef CAS
 .
. - M. Segall, R. Shah, C. Pickard and M. Payne, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16317 CrossRef CAS
 .
.
|
| This journal is © The Royal Society of Chemistry 2015 |
Click here to see how this site uses Cookies. View our privacy policy here.  *b,
Suhong Zhanga,
Jinliang Ninga,
Na Suna,
Mingzhen Maa and
Riping Liua
*b,
Suhong Zhanga,
Jinliang Ninga,
Na Suna,
Mingzhen Maa and
Riping Liua




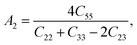





 , and the weak dependence of the bulk modulus on temperature, the trend of the volume thermal expansion coefficient is similar to the heat capacity, i.e., it increases rapidly with temperature at low temperatures (α(T) ∼ T3) and gradually approaches a very slow linear increase at high temperatures (T > 300 K). As Fig. 12(a) shows, our results are in good agreement with available experimental data43 at relatively high temperatures in a range of 300–1000 K, and one can expect that if there were available experimental data at low temperatures, good agreement will be reached with our calculated results. Additionally, as seen from Fig. 12(b), at a given temperature, the thermal expansion coefficient decreases drastically under low pressures and the curve becomes flat with pressure increasing.
, and the weak dependence of the bulk modulus on temperature, the trend of the volume thermal expansion coefficient is similar to the heat capacity, i.e., it increases rapidly with temperature at low temperatures (α(T) ∼ T3) and gradually approaches a very slow linear increase at high temperatures (T > 300 K). As Fig. 12(a) shows, our results are in good agreement with available experimental data43 at relatively high temperatures in a range of 300–1000 K, and one can expect that if there were available experimental data at low temperatures, good agreement will be reached with our calculated results. Additionally, as seen from Fig. 12(b), at a given temperature, the thermal expansion coefficient decreases drastically under low pressures and the curve becomes flat with pressure increasing.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.





