Fluorescent phenanthridine-based calix[4]arene derivatives: synthesis and thermodynamic and computational studies of their complexation with alkali-metal cations

Abstract

New fluorescent calix[4]arene derivatives 1, 2, and 3 were synthesized by introducing phenanthridine moieties at a lower calixarene rim. It was shown that due to the prominent fluorescence of compounds 1 and 3, they could be considered as potential sensitive fluorimetric cation sensors. Complexation of the prepared compounds with alkali-metal cations was studied at 25 °C in acetonitrile–dichloromethane and methanol–dichloromethane solvent mixtures (φ = 0.5) by means of fluorimetric, spectrophotometric, potentiometric, and microcalorimetric titrations as well as NMR spectroscopy. The stability constants of the corresponding complexes were determined, as were the enthalpies and entropies of the complexation reactions. In addition, equilibrium constants of ion-pairing reactions between alkali-metal cations and several anions in the solvents used were measured conductometrically. It was found that the cation-binding affinity of ligand 1 with four phenanthridine subunits was much higher than that of 2 and 3, with the complex stabilities in all cases being significantly lower in methanol–dichloromethane mixture compared to that in acetonitrile–dichloromethane. These findings were thoroughly discussed by taking into account the determined thermodynamic complexation data, structural properties of the ligand and free and complexed cations, as well as the solvation abilities of the solvents examined. The conclusions made in that way were corroborated by the results of the molecular dynamics simulations of the systems studied. An attempt to get an insight into the possible structures of the alkali-metal cation complexes with ligand 1 was made by carrying out the corresponding density functional theory calculations.

---

Introduction

Calixarene derivatives have been widely used as macrocyclic host molecules. Depending on the macrocycle cavity size and the substituents at their upper and/or lower rim, calixarenes can encapsulate many different ions and neutral molecules.^1–3 Their three-dimensional binding site can be appropriately organized by relatively easy functionalization of both rims to obtain receptors with desired properties.⁴ The inclusion abilities of calixarene derivatives enable their numerous applications, from sensoring and removal of biologically and environmentally relevant ions, to catalysis and use as biomimetic receptors in the studies of enzyme–substrate reactions.^5,6

Among the variety of calixarene based derivatives carrying functionalities at the lower macrocyclic rim, the receptors with nitrogen donor atoms have been used as hosts for cations and anions.^2,7,8 Most of the research involving such calixarenes as cation receptors has been directed towards design of selective ligands for transition-metal cations.^9–14 In addition, they have also been recognized as interesting biomimetic compounds.^15,16 On the other hand, their abilities for complexation of alkali- and alkaline earth metal cations have been far less explored, despite the fact that they are capable of binding such cations quite efficiently,¹⁷ and in some cases with remarkable selectivity.¹⁸

It should be noted that the process of calixarene–cation complex formation in solution is often strongly influenced by solvation of the reactants and the complex formed.^19–25 In addition, in non-aqueous solutions ion-pairing between free and complexed cation and an anion can significantly affect the cation-binding reaction.^19,26

As already mentioned, the unique topology of calixarenes offers a wide range of scaffolds, making them perfect platforms for sensors. By introducing fluorescent substituents, e.g. anthracene, naphthalene, pyrene, dansyl, or tryptophan groups into the calixarene moiety, it is possible to prepare highly sensitive sensors for variety of species, which have received considerable attention in recent years.^27–33 The fluorescent and cation binding properties of phenanthridines attached to azacrowns are well known.^34–36 For that reason, in the present work it has been considered as a convenient substituent for obtaining fluorescent calixarenes. Thus, three novel calix[4]arene derivatives with phenanthridine subunits at the lower rim, namely 5,11,17,23-tetra-tert-butyl-25,26,27,28-tetrakis-((phenanthridine-6-yl)methoxy)calix[4]arene (1, Scheme 1), 5,11,17,23-tetra-tert-butyl-25,27-bis-((phenanthridine-6-yl)methoxy)-26,28-dihydroxycalix[4]arene (2, Scheme 1), and 5,11,17,23-tetra-tert-butyl-25,27-bis-((phenanthridine-6-yl)methoxy)-26,28-dimethoxycalix[4]arene (3, Scheme 1) were synthesized. Their binding affinities towards alkali-metal cations in acetonitrile–dichloromethane (MeCN–CH₂Cl₂) and methanol–dichloromethane (MeOH–CH₂Cl₂) solvent mixtures were studied by means of an integrated approach comprising experimental (UV, fluorescence, and NMR spectroscopies, potentiometry, conductometry, microcalorimetry) and computational (DFT, classical molecular dynamics) techniques. The solvent effect on the reactions studied was addressed as well. This has provided a rather detailed insight into the factors governing the complexation processes and shed light on the possible structures of the ligands and their alkali-metal cation complexes.

Scheme 1 Synthesis of compounds 1, 2, and 3. Reagents and conditions: (i) K₂CO₃, KI, acetone (Ar) Δ; (ii) (1) K₂CO₃, MeCN, Δ, (2) KOH, Δ; (iii) DMF (Ar) 0 °C, NaH.

Results and discussion

Syntheses

The syntheses of calixarene derivatives 1, 2, and 3 are shown in Scheme 1. The compounds were obtained in one synthetic step by addition of 6-(chloromethyl)phenanthridine to calix[4]arene or 1,3-dimethoxy-p-tert-butylcalix[4]arene. The tetrasubstituted derivative, compound 1, was obtained in 43% yield, whereas compounds 2 and 3 were obtained in 63% and 67% yield, respectively. Compound 2 was also prepared by microwave-assisted synthesis with higher yield (88%). The amount of 6-(chloromethyl)phenanthridine added to reaction mixture determined the outcome of the reaction. When it was added in large excess (100% excess per reactive group) reaction yielded only tetrasubstituted calixarene product. On the contrary, when 6-(chloromethyl)phenanthridine was added to calixarene in equimolar quantities (1 : 1 per OH group), exclusively disubstituted product was obtained. Calixarene derivatives were characterized by spectroscopic methods, elemental analysis, and high-resolution mass spectrometry. The ¹H NMR spectrum of 1 in CDCl₃ (Fig. S1 and Table S1, ESI†) showed one singlet due to tert-butyl groups (δ = 0.98 ppm) and another singlet due to calixarene aromatic protons (δ = 6.54 ppm), a pattern characteristic for the cone conformation and C₄ symmetry of tetrasubstituted calix[4]arene.^20,52 Two sets of doublets due to the bridging methylene protons (δ = 2.49 ppm and 4.09 ppm) and a singlet due to ArOCH₂ protons (δ = 5.41 ppm) indicated the structural rigidity or the time-averaged cone conformation resulting from the transition between two flattened cone C_2v conformations.^3,37 The complete assignment of signals corresponding to phenanthridine protons was enabled by 2D (COSY and NOESY) ¹H NMR spectra (Fig. S2 and S3, ESI†). The ¹H NMR spectrum of 2 in CDCl₃ (Fig. S4 and Table S2, ESI†) showed two singlet signals corresponding to tert-butyl groups at δ = 0.98 ppm and 1.23 ppm and another two singlets corresponding to calixarene aromatic protons at δ = 6.80 ppm and 6.97 ppm (depending on the substituent in the p-position: hydroxyl and phenanthridinyl groups), confirming that the compound was a disubstituted calixarene derivative. Also, two sets of doublets (δ = 3.22 ppm and 4.42 ppm) and a singlet (δ = 5.69 ppm) indicated the cone conformation. A rather high chemical shift of OH protons (7.68 ppm) indicated the presence of intramolecular OH⋯O–C hydrogen bonds at the lower rim which stabilized the cone conformation by preventing rotation through the annulus. The signals in the ¹H NMR spectra of compound 2 were shifted towards higher values than in the case of compound 1. This is the result of deshielding of the protons due to the formation of H-bond between the phenolic hydroxyl group and neighboring ether oxygen atom. Contrary to 1 and 2, in ¹H NMR spectrum of disubstituted calix[4]arene 3 recorded in chloroform solution at 25 °C (Fig. S5 and Table S3, ESI†) most of the signals were broad, which suggested fast interconversion between several ligand conformations.³⁸ This was due to a higher conformational flexibility of compound 3. Obviously, two –OCH₃ groups at the lower rim were not bulky enough to prevent conformational interconversion by rotation through the calixarene cavity. On the other hand, addition of LiClO₄ or NaClO₄, i.e. the process of metal–ion binding, caused the broad peaks in ¹H NMR spectrum of compound 3 to sharpen, and at the same time the pattern of signals characteristic for the cone conformation of approximate C₂ symmetry appeared. This indicated that both complexes formed adopted the cone or averaged cone conformation (as described later in detail).

Cation complexation studies

Due to the low solubilities of the studied calixarene derivatives in solvents of moderate permitivities, their complexation abilities towards alkali-metal cations were studied in mixed solvents, namely MeCN–CH₂Cl₂ and MeOH–CH₂Cl₂ (volume fraction, φ = 0.5).

In solvents of low dielectric constants, besides the complexation reaction it may be necessary to take into account a competitive process of ion association between the free cation and the anion of the salt used. In addition, formation of ion pair comprising complexed metal–ion and anion can also occur in such solvents. However, as the latter process involves a quite large cation which has much lower tendency to form ion pairs than the free metal ion,³⁹ its contribution to the overall stability of the cation–calixarene complex can be considered negligible. On the other hand, the former reaction should be accounted for in the course of the process of complex stability constant determination.

In this work, precise conductivity measurements provided information on alkali-metal cation–anion interactions. The relative permittivity (ε_r) values for binary solvent mixtures MeCN–CH₂Cl₂ (φ = 0.5) and MeOH–CH₂Cl₂ (φ = 0.5) were calculated from literature data⁴⁰ assuming that the mixtures were ideal, while their densities and viscosities were determined experimentally (Table S7, ESI†). The limiting molar conductivities and ion-association constants determined using the Lee-Wheaton conductance equation in Pethybridge and Taba version (LWPT model),⁴¹ are listed in Table S8 (ESI†). The corresponding data for KCl, RbNO₃ and RbCl in MeCN–CH₂Cl₂ could not be obtained due to the poor solubilities of these salts in this solvent mixture. The dependences of molar conductivity of LiClO₄, NaClO₄, KCl, RbNO₃ and RbCl on their concentrations in MeCN–CH₂Cl₂ and MeOH–CH₂Cl₂ mixtures are presented in Fig. S13–19 (ESI†).

Solvent: acetonitrile–dichloromethane. As examples, spectrophotometric titrations of 1 with Li⁺ and Rb⁺ are shown in Fig. 1, whereas the corresponding titrations with the other alkali-metal cations are given in ESI (Fig. S20 and S21†). Upon stepwise addition of Li⁺, Na⁺, K⁺, or Rb⁺ salt solution in MeCN–CH₂Cl₂ mixture to solution of 1 in the same solvent, significant changes of its UV spectrum were observed accompanied with the simultaneous occurrence of several isosbestic points. As the spectrum of free 1 (Fig. 1) closely resembled that of the phenanthridine subunit (Fig. S22, ESI†), it could be concluded that at least some of phenanthridine subunits were directly involved in the cation coordination, as suggested by the results of the computational studies (see later). In the cases of titrations of 1 with LiClO₄ and NaClO₄, a linear relationship of absorbance vs. the amount of cation added were observed up to the ratio n(M⁺)/n(1) ≈ 1, followed by a break in the titration curve (Fig. 1a and S20, ESI†). These findings revealed a formation of 1 : 1 complexes and a rather strong complexation.

Fig. 1 Spectrophotometric titration of (a) 1 (c = 1.82 × 10⁻⁴ mol dm⁻³) with LiClO₄ (c = 1.65 × 10⁻³ mol dm⁻³) and (b) 1 (c = 1.79 × 10⁻⁴ mol dm⁻³) with RbNO₃ (c = 1.02 × 10⁻³ mol dm⁻³) in MeCN–CH₂Cl₂ mixture (φ = 0.5) at (25.0 ± 0.1) °C. Spectra are corrected for dilution. Insets: absorbance at 349 nm and 356 nm, respectively, as a function of cation to ligand molar ratio. ○ experimental; – calculated.

As follows from the above considerations, the stability constant of Na1⁺ in MeCN–CH₂Cl₂ solvent mixture could not be determined spectrophotometrically because of its high value. Therefore, it was determined potentiometrically (Fig. 2a, Table 1).

Fig. 2 Potentiometric titrations of (a) NaClO₄ (c = 1.01 × 10⁻⁴ mol dm⁻³) with 1 (c = 7.49 × 10⁻⁴ mol dm⁻³) and (b) NaClO₄ (c = 9.90 × 10⁻⁴ mol dm⁻³) with 3 (c = 1.02 × 10⁻² mol dm⁻³) in MeCN–CH₂Cl₂ mixture (φ = 0.5) at (25.0 ± 0.1) °C; I_c = 0.01 mol dm⁻³ (Et₄NClO₄). ○ experimental; – calculated.

Table 1 Stability constants of the complexes of compounds 1, 2, and 3 with alkali-metal cations in MeCN–CH₂Cl₂ and MeOH–CH₂Cl₂ solvent mixtures (φ = 0.5) at (25.0 ± 0.1) °C. Uncertainties are given in parentheses as standard errors of the mean (N = 3)

log K
Acetonitrile–dichloromethane
	Li^+	Na^+	K^+	Rb^+	Cs^+
a Estimation based on spectrophotometric data. b Spectrophotometric titrations. c Potentiometric titrations. d Fluorimetric titrations. e Insufficient spectral changes. f Complexation was not observed under the conditions used.
1	>6^a	8.05(1)^c	5.57(3)^b	3.98(1)^b	—^e
2	2.77(1)^b	2.74(1)^b	—^e	—^e	—^e
3	5.52(2)^b	4.87(1)^b	—^e	—^e	—^e
	5.57(1)^d	5.19(1)^c
		5.02(1)^d

---

Methanol–dichloromethane
	Li^+	Na^+	K^+	Rb^+	Cs^+
1	—^e	5.19(1)^b	4.49(1)^b	2.94(1)^b	—^e
2	—^e	—^e	—^e	—^e	—^e
3	—^f	2.36(2)^b	—^e	—^e	—^f
		2.49(1)^d

---

Stability constant of K1⁺ complex was not as large, so its value (Table 1) was determined by processing the spectrophotometric data (Fig. S21, ESI†). Although observable, the absorbance changes in the titration of 1 with cesium nitrate and cesium chloride were insufficient to enable their reliable quantitative analysis. The attempts were made to prepare solutions of concentrations large enough, but the cesium salts used were rather poorly soluble in MeCN–CH₂Cl₂ solvent mixture.

The fluorescence intensity of compound 1 in MeCN–CH₂Cl₂ solvent mixture showed linear dependence on its concentration up to ≈7.5 × 10⁻⁶ mol dm⁻³. However, the addition of alkali-metal cations caused irreproducible changes in emission spectrum of this ligand. Further examinations showed that irradiation of the solution of compound 1 by UV light had a significant influence on its emission and NMR spectra, and exposure of solution of Na1⁺ complex to UV light caused even more pronounced changes. This was an indication of photochemical decomposition of 1 in this solvent. In addition, it can be concluded that complexation enhanced this process, probably by positioning phenanthridine units in a certain spatial arrangement. For that reason, although compound 1 and its complexes were photostable enough to enable spectrophotometric experiments, it was not possible to determine the stability constants of the complexes fluorimetrically.

¹H NMR titrations of compound 1 with LiClO₄ and NaClO₄ in CD₃CN–CDCl₃ were also performed (Fig. S23 and S24, ESI†). The chemical shifts of Li1⁺ and Na1⁺ protons showed significant changes relative to those of the free ligand, particularly for the aromatic, axial and equatorial methylene-bridge, and phenanthridine protons. Strong deshielding effects observed could be attributed to the interaction of the cation with the functionalized sites at the lower rim. Changes in the phenanthridine region indicated involvement of these groups in complexation.

In MeCN–CH₂Cl₂ solvent mixture complexation of compound 2 was observed only for Li⁺ and Na⁺ cations (Fig. S25, ESI†). The stability constants obtained by the corresponding spectrophotometric titrations were significantly smaller than in the case of compound 1 (Table 1). The addition of Li⁺ caused increase in the intensity of absorbance, bathochromic shifts of minima and maxima and the appearance of several isosbestic points. On the other hand, addition of Na⁺ caused very small changes in the UV spectrum of compound 2, but sufficient to enable stability constant determination (Table 1). Salts of the other alkali-metal cations were not soluble enough in this solvent to allow us to carry out reliable UV titrations.

In the course of ¹H NMR titration of ligand 2 with LiClO₄ in CD₃CN–CDCl₃ solvent mixture (Fig. S26, ESI†), the most pronounced changes were observed for the signal corresponding to OH protons, which shifted from 8.89 ppm to 9.22 ppm. Significant changes occurred also in the region corresponding to the phenanthridine protons indicating involvement of these groups in the complexation process. All spectra recorded during this titration showed only one signal for each proton suggesting that the exchange between free and complexed ligand was fast on the ¹H NMR time scale.

Contrary to 1, compound 2 showed almost negligible fluorescence. That can be mostly accounted for by considering that 1 has four fluorescent subunits whereas 2 has only two. Furthermore, in 1 bulky phenanthridine groups sterically hinder the rotation and increase rigidity of the structure, whereas compound 2 has higher degree of flexibility enabling nonradiative relaxation accompanied by significant reduction of fluorescence. It should be noted that addition of Li⁺ and Na⁺ cations caused very small increase in fluorescence intensity, insufficient to enable fluorimetric stability constant determination.

The shapes of spectrophotometric titration curves of 3 with alkali-metal cations in MeCN–CH₂Cl₂ mixture suggested the formation of less stable complexes than in the case of 1, which was expected due to the differences in their structures. The considerable changes in absorbance were again observed in the case of titrations with LiClO₄ and NaClO₄ (Fig. S27 and S28, ESI†). The results of multivariate nonlinear regression analyses of the corresponding spectra, i.e. stability constants of Li3⁺ and Na3⁺, are given in Table 1. These values are almost 1000 times larger than those obtained for Li2⁺ and Na2⁺. That can be explained by considering the possibility of intramolecular hydrogen bonds formation in compound 2 which competes with cation binding process. In addition, lower basicity of ligand 2 oxygen atoms compared to compound 3 should be also taken into account.

The addition of potassium, rubidium, or cesium cation salt caused very small, almost negligible changes in the UV spectrum of 3 solution. That pointed out a quite small affinity of this compound for the larger alkali-metal cations.

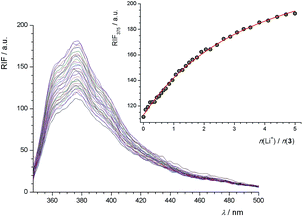
In the course of the fluorimetric titration of 3 with Na⁺ cation, a rather large increase of fluorescence intensity was observed (Fig. S29, ESI†). Such an increase was also found in the cases of Li⁺ (Fig. 3) and K⁺ (Fig. S30, ESI†), but it was less pronounced. This effect of cation addition on fluorescence intensity can be explained by considering the possibility of photoinduced electron transfer (PET) from the HOMO of the ether oxygen atoms to that of the excited phenanthridine fluorophore, causing fluorescence quenching of the latter. Upon cation binding the redox potential of the electron donor is raised so that the relevant HOMO becomes lower in energy than that of the fluorophore. Consequently, PET is no longer possible and fluorescence quenching is suppressed.^27,42

Fig. 3 Fluorimetric titration of 3 (c = 1.9 × 10⁻⁶ mol dm⁻³) with LiClO₄ (c = 3.6 × 10⁻⁵ mol dm⁻³) in MeCN–CH₂Cl₂ mixture (φ = 0.5) at (25.0 ± 0.1) °C; λ_ex = 333 nm, excitation slit 7.5 nm, emission slit 7.5 nm. Spectra are corrected for dilution. Inset: relative fluorescence intensity at 375 nm as a function of cation to ligand molar ratio; ○ experimental data; – calculated values.

The stability constants of Li3⁺, Na3⁺, and K3⁺ complexes determined fluorimetrically are listed in Table 1.

Equilibrium constant for complexation reaction of 3 with Na⁺ was also determined by direct potentiometric titration (Fig. 2b, Table 1), and is in a rather good agreement with the values obtained spectrophotometrically and fluorimetrically.

Addition of NaClO₄ and LiClO₄ to solution of compound 3 in CD₃CN–CDCl₃ (Fig. 4 and S31, ESI†) caused dramatic changes in the appearance of ¹H NMR spectrum of the ligand. All the signals sharpened and a pattern of signals pointing out cone as the prevailing conformation appeared. In the case of titration of compound 3 with NaClO₄, 3-fold excess of Na⁺ over 3 revealed a typical pair of closely positioned, equally intense singlets corresponding to the tert-butyl group protons as well as a pair of doublets at 3.41 ppm and 4.32 ppm characteristic for axial and equatorial protons of methylene group bridging two aryl units.³⁸

Fig. 4 ¹H NMR titration of ligand 3 (c = 2.91 × 10⁻³ mol dm⁻³) with NaClO₄ (c = 3.22 × 10⁻³ mol dm⁻³) in CD₃CN–CDCl₃ mixture (φ = 0.5) at 25.0 °C; n(Na⁺)/n(3) = 0 (1); 0.33 (2); 0.66 (3); 1 (4); 1.5 (5); 2 (6); 3 (7).

The complexation of alkali-metal cations by compounds 1 and 3 was also investigated by means of microcalorimetric titrations. Standard reaction enthalpies and equilibrium constants were computed by a nonlinear least-squares analysis of calorimetric data. Standard reaction Gibbs energies and entropies were obtained by using the equations Δ_rG° = −RT ln K and Δ_rG° = Δ_rH° − TΔ_rS°, respectively. The obtained thermodynamic parameters are listed in Table 2. It should be noted that the stability constants determined calorimetrically are in rather good agreement with those measured by other techniques (Table 1). As examples, experimental and calculated data corresponding to the titrations of 1 and 3 in MeCN–CH₂Cl₂ with K⁺ and with Na⁺ are shown in Fig. 5.

Table 2 Thermodynamic parameters for complexation of alkali-metal cations with 1 and 3 in MeCN–CH₂Cl₂ and MeOH–CH₂Cl₂ (φ = 0.5) obtained by microcalorimetry at (25.0 ± 0.1) °C. Uncertainties are given in parentheses as standard errors of the mean (N = 3)

	log K	ΔrG° kJ mol^−1	ΔrH° kJ mol^−1	ΔrS° J K^−1 mol^−1
a Determined potentiometrically.
Acetonitrile–dichloromethane
1
Li^+	6.80(3)	−38.8(2)	−20.8(4)	61(2)
Na^+	8.05(1)^a	−45.96(6)	−43.7(6)	8(2)
K^+	5.67(6)	−32.4(4)	−35(1)	−8(4)
Rb^+	4.09(4)	−23.3(2)	−28.2(5)	−16(2)
3
Li^+	5.69(3)	−32.5(1)	−30.6(5)	6(1)
Na^+	5.19(3)	−29.6(2)	−39.6(5)	−34(2)
Methanol–dichloromethane
1
Na^+	5.16(5)	−29.4(3)	−18.8(4)	36(2)
K^+	4.24(4)	−24.2(2)	−21.2(5)	10(2)

---

Fig. 5 Microcalorimetric titration of (a) 1 (c = 9.53 × 10⁻⁵ mol dm⁻³, V = 1.4182 cm³) with KClO₄ (c = 1.10 × 10⁻³ mol dm⁻³) (b) 3 (c = 2.06 × 10⁻⁴ mol dm⁻³, V = 1.4182 cm³) with Na[B(Ph)₄] (c = 1.84 × 10⁻³ mol dm⁻³) in MeCN–CH₂Cl₂ mixture (φ = 0.5) at (25.0 ± 0.1) °C; dependence of successive enthalpy change on n(K⁺)/n(1) and n(Na⁺)/n(3) ratio, respectively; ○ experimental; – calculated. Insets: raw calorimetric data.

As can be seen by inspecting the data presented in Table 2, the preference of the examined macrocycles towards sodium with respect to the other examined cations in MeCN–CH₂Cl₂ is predominantly a consequence of the strongly favourable enthalpic contribution to the standard complexation Gibbs energy. This is in accordance with the calorimetric investigations regarding the binding abilities of calix[4]arenes with oxygen-donor atoms in MeCN,^19,20,22,23 and can be rationalized by a compatibility of the Na⁺ and the ligand ion-bonding site sizes. The positive complexation entropy for sodium binding with 1 can, at least partly, be explained by taking into account the preferential solvation (with MeCN) of alkali metal cations in the investigated mixed solvent. Namely, the standard transfer Gibbs energies (Table S9, ESI†) of alkali-metal cations from CH₂Cl₂ to both methanol and acetonitrile are in all cases strongly favourable, especially for smaller cations. In addition, during the MD simulations of alkali-metal salts in mixed solvents (Fig. S32, Tables S10 and S11, ESI†) the cations were always surrounded with either acetonitrile or methanol molecules, but never with dichloromethane. Accordingly, the preferential solvation of cations in solvents used with acetonitrile and methanol molecules can be expected. This could in turn result in positive entropy changes accompanying the alkali-metal cation desolvation due to mixing of released solvent molecules with the solvent bulk.

The complexation entropy is most favourable for Li⁺ binding with 1, whereas the absolute value of complexation enthalpy is the lowest for this reaction. As described in several papers regarding the complexation of Li⁺ in pure acetonitrile,^20,22,23 such large positive reaction entropy is mainly due to the strongest solvation of this cation among the others. On the other hand, the cation desolvation process is for that reason energetically quite demanding. The value of reaction enthalpy for K⁺ complexation with 1 is between those for Li⁺ and Na⁺, whereas the entropic contribution to the binding Gibbs energy is in this case considerably lower. The enthalpic contribution to the complexation of Rb⁺ is about 8 kJ mol⁻¹ less favourable than in the case of K⁺. That is, together with a lower Δ_rS° value compared to the other cations, reflected in the lowest stability of Rb1⁺ species.

By comparing the standard thermodynamic reaction parameters for complexation of Li⁺ by compounds 1 and 3 one can observe that, although the affinity of 1 for Li⁺ is higher than that of 3 (Table 2), this is not a result of the enthalpic stabilization of Li1⁺ caused by a possible cation coordination by larger number of nitrogen atoms. Actually, the reaction enthalpy of Li3⁺ formation is notably more favourable than that of Li1⁺. However, the opposite holds for the corresponding reaction entropies, which eventually results in larger stability of the complexes with the ligand bearing four phenanthridine subunits. As already mentioned, compound 1 in solution exists in cone conformation. On the other hand, the ¹H NMR spectrum of ligand 3 in CD₃CN–CDCl₃ mixture indicates the presence of several conformers which upon cation complexation adopt the cone conformation (Fig. 4 and S31, ESI†). The ligand 1 is hence better suited for cation binding because of the proper orientation of its functionalities at the lower rim. As a consequence, the cation complexation with ligand 3 is more entropically demanding process than that with ligand 1.

The stability of Na3⁺ is much lower than that of Na1⁺. This is mainly a consequence of a much more favourable reaction entropy of complexation with receptor 1 than with 3, whereas the reaction enthalpies for formation of Na1⁺ and Na3⁺ are rather similar (Table 2).

It is interesting to compare the stabilities of Li3⁺ and Na3⁺ species (Tables 1 and 2). Evidently, the larger equilibrium constant of lithium complex formation is the result of more favourable complexation entropy, since the formation of Na3⁺ is more enthalpically advantageous (Table 2). That could be again, at least partially, explained by the higher desolvation entropy of lithium cation.

Solvent: methanol–dichloromethane. In MeOH–CH₂Cl₂ solvent mixture spectral changes observed during UV titration of calixarene derivative 1 with LiClO₄ were very small. This indicated that the stability of the corresponding complex was quite low. On the other hand, by processing the spectrophotometric data of titration of 1 with Na⁺, a quite high stability constant of Na1⁺ complex was obtained (Table 1). The spectral changes (Fig. S33, ESI†) were similar to those observed in MeCN–CH₂Cl₂ solvent. The same holds for the spectrophotometric titrations of 1 with KCl (Fig. 6) and RbNO₃ (Fig. S34, ESI†). The stability constants determined by analyzing the corresponding data are given in Table 1.

Fig. 6 Spectrophotometric titration of 1 (c = 1.28 × 10⁻⁴ mol dm⁻³) with KCl (c = 2.56 × 10⁻³ mol dm⁻³) in MeOH–CH₂Cl₂ mixture (φ = 0.5) at (25.0 ± 0.1) °C. Spectra are corrected for dilution. Inset: absorbance at 333 nm, as function of cation to ligand molar ratio. ○ experimental; – calculated.

Addition of cesium chloride or nitrate to the solution of 1 had no significant effect on its UV spectrum, indicating that under conditions used no observable complexation took place.

Quite different than in MeCN–CH₂Cl₂ mixture, in MeOH–CH₂Cl₂ compound 1 and its complexes were much more photostable. Changes in the emission spectrum of 1 upon addition of alkali-metal cations were reproducible. That enabled fluorimetric titrations that yielded reliable results. Stability constants determined fluorimetrically agreed quite well with those determined spectrophotometrically (Table 1).

While the addition of Li⁺ (even in relatively large concentrations) to solution of 1 did not influence its fluorescence (Fig. S35, ESI†), the addition of NaClO₄ (Fig. 7) caused a significant increase in fluorescence intensity. Fluorimetric titrations of 1 with potassium and rubidium salts in MeOH–CH₂Cl₂ were also carried out (Fig. S36 and S37, ESI†). The stability constants of Na1⁺, K1⁺, and Rb1⁺ complexes determined fluorimetrically are listed in Table 1.

Fig. 7 Fluorimetric titration of 1 (c = 3.8 × 10⁻⁶ mol dm⁻³) with NaClO₄ (c = 6.0 × 10⁻⁵ mol dm⁻³) in MeOH–CH₂Cl₂ mixture (φ = 0.5) at (25.0 ± 0.1) °C; λ_ex = 333 nm, excitation slit 5 nm, emission slit 5 nm. Spectra are corrected for dilution. Inset: relative fluorescence intensity at 375 nm as a function of cation to ligand molar ratio; ○ experimental; – calculated.

It is interesting to note that while the addition of Na⁺ caused an increase in the fluorescence intensity of compound 1, the addition of K⁺ or Rb⁺ caused the opposite effect, its decrease. This can be ascribed to different interactions stabilizing the resulting complexes. It is well known that calix[4]arene derivatives can bind solvent molecules into their hydrophobic cavity.^8,23,25 As shown by molecular dynamics simulations (see later), in the case of complex Na1⁺ in MeOH–CH₂Cl₂, an adduct with a methanol molecule can be formed in which the oxygen atom of MeOH coordinates Na⁺, shifting it further towards the hydrophobic cavity. Hence, Na⁺ is coordinated by the ether oxygen atoms while its interaction with phenanthridine subunits is significantly reduced. In the case of larger cations K⁺ and Rb⁺, the inclusion of MeOH also occurred, but with oxygen atom of MeOH oriented towards the tert-buthyl groups, leaving the cations coordinated by both ether oxygen atoms and phenanthridine subunits. These differences probably reflected in the emission spectra. The addition of Na⁺ to the solution of 1 caused inhibition of PET and the increase of fluorescence intensity. On the contrary, weaker interactions of K⁺ and Rb⁺ with oxygen atoms of calixarene derivative enabled PET which, together with their interactions with phenanthridine subunits, resulted in fluorescence quenching.

Changes in the ¹H NMR spectrum of compound 1 observed in the course of its titration with NaClO₄ in CD₃OD–CDCl₃ (Fig. S38, ESI†) were similar to those previously described in the case of CD₃CN–CDCl₃ solvent mixture. The main difference was in shifts of signals corresponding to axial protons: in CD₃CN–CDCl₃ they were shifted towards lower field whereas in CD₃OD–CDCl₃ solvent they experienced upfield shift. This could again be ascribed to the influence of methanol molecule inclusion into the calixarene hydrophobic cavity and its interaction with Na⁺, as observed by molecular dynamics simulations (see later). On the other hand, acetonitrile molecule included in the ligand basket is presumably oriented with its nitrogen atom pointing towards tert-buthyl groups and does not directly interact with sodium cation (see later).

Compound 2 did not bind any of the investigated cations in MeOH–CH₂Cl₂ solvent mixture under the conditions used.

In the course of the UV titrations of 3 with Li⁺, K⁺, Rb⁺, and Cs⁺ salts in MeOH–CH₂Cl₂ solvent mixture, no significant changes in absorbance were observed, suggesting very small affinity of the ligand 3 for these cations in this solvent. The complexation of compound 3 was observed only in the case of Na⁺ cation (Fig. S39, ESI†). However, the stability constant of Na3⁺ species (Table 1) was much lower than in MeCN–CH₂Cl₂.

Methanol–dichloromethane solution of 3 showed almost negligible fluorescence, even at the compound concentrations larger than 10⁻⁵ mol dm⁻³. Addition of sodium perchlorate to solution of 3 caused significant increase of its fluorescence intensity (Fig. S40, ESI†). Stability constant of Na3⁺ complex calculated by processing the fluorimetric data is given in Table 1, and agrees quite well with that determined spectrophotometrically.

As already stated, spectrophotometric experiments suggested that, although compound 1 very strongly bound Li⁺ in MeCN–CH₂Cl₂ mixture (Table 1), in MeOH–CH₂Cl₂ no complexation could be observed. This huge difference is by large the consequence of a remarkable difference in cation solvation in the solvents used (Δ_tG°(MeCN → MeOH) = −21 kJ mol⁻¹).⁴³ Similar was previously noticed in the case of Li⁺ complexation by several calixarene derivatives in methanol and acetonitrile.^20,22,23 On the other hand, the complexation of sodium cation is quite favourable (Table 2 and Fig. S41, ESI†), both in terms of enthalpy and entropy. One of the reasons why the entropic stabilization in MeOH–CH₂Cl₂ is much larger in comparison to MeCN–CH₂Cl₂ (the reaction entropy for sodium complexation is positive but rather low) could be the inclusion of an acetonitrile molecule into the hydrophobic cavity of the host, as observed by MD simulations (see later). We have previously shown that the formation of such an adduct with acetonitrile in the case of calix[4]arene secondary amide derivative in PhCN is accompanied by quite favourable reaction enthalpy and strongly unfavourable reaction entropy.²⁵ Such negative entropy changes could largely counterbalance the entropically advantageous cation desolvation in MeCN–CH₂Cl₂. On the other hand, the exothermic inclusion of acetonitrile molecule into the macrocycle cavity almost certainly contributes to the larger stabilities of alkali-metal cation complexes in MeCN–CH₂Cl₂ as compared to the complex species in MeOH–CH₂Cl₂, because, according to the results of MD simulations, the inclusion of solvent molecule into the calixarene cone in the latter solvent mixture is less pronounced. Another factor which also contributes to the higher complex stabilities in MeCN–CH₂Cl₂ than in MeOH–CH₂Cl₂ is stronger solvation of the cation by MeOH molecules (Δ_tG° (MeCN → MeOH) = −7 kJ mol⁻¹).⁴³

As can be seen from the data listed in Tables 1 and 2, the complexation of potassium with 1 in MeOH–CH₂Cl₂ is mostly enthalpically controlled, although the entropy contribution to the corresponding reaction Gibbs energy is also favourable. However, the Δ_rS° value is lower than in the case of Na⁺ complexation, presumably due to the lower gain in entropy by desolvation of K⁺ cation. Due to the rather low stability constant of Rb1⁺ complex (Table 1) and the scarce solubility of rubidium tetraphenylborate, the thermodynamic parameters for Rb⁺ complexation could not be determined calorimetrically. It should be noted that the thermodynamic reaction quantities for Na⁺ binding with 3 in MeOH–CH₂Cl₂ also could not be determined calorimetrically because the enthalpy changes measured in the course of the corresponding titrations were too low.

Molecular dynamics simulations

Solvent: acetonitrile/dichloromethane. In order to obtain an insight into the structures of calixarene ligands 1 and 3 and their complexes with alkali-metal cations in solution, classical molecular dynamics simulations were performed. For both ligands, immediately at the beginning of the simulation the inclusion of solvent molecules in the calixarene hydrophobic cavity was observed. The accompanying conformational changes from the initial flattened cone to nearly regular cone were reflected in the distances of the opposing aryl carbon atoms that are directly bound to tert-butyl groups (Fig. S42 and Table S12, ESI†). In the case of ligand 1 the sequential inclusion of 3 different CH₂Cl₂ molecules took place, followed by the inclusion of MeCN molecule which occupied the cone for the most of the simulation time (Fig. S43a, ESI†). The inclusion of solvent molecules was also observed in the MD simulations of ligand 3, where acetonitrile molecule entered the macrocycle hydrophobic cavity at the beginning, and remained there until the end of simulation time (Fig. S43b, ESI†). In both cases the MeCN molecule was oriented with the nitrile group pointed towards the bulk. Acetonitrile adducts were more stable than the ones with dichloromethane molecules as the former were present for the most of the simulation time and exhibited a slower exchange of solvent molecules bound to the hydrophobic cavity. For both 1 and 3 the shape of the cone remained somewhat flattened, although it resembled the regular square cone conformation. This is most likely due to the steric effects of the large substituents at the lower rim of the investigated ligands. The overall interactions of dichloromethane with the ligands and their adducts are energetically more favourable than those with acetonitrile molecules, the difference being in the range of 90–250 kJ mol⁻¹ (Table S13, ESI†).

The results of the MD simulations of alkali-metal cation complexes with ligands 1 and 3 revealed that cations are coordinated with all ether oxygen atoms and variable number of nitrogen atoms of the phenanthridine subunits. Calixarene hydrophobic cavity is occupied by solvent molecules for the most of the simulation time (Fig. S46 and S48, ESI†). As was the case with the uncomplexed ligands 1 and 3, acetonitrile adducts of their complexes were more stable than those with dichloromethane molecules, and were present in the cone for the most of the simulation time (Tables S14–S19, ESI†). The conformation of the calixarene basket in ML⁺ adducts with MeCN was very close to the square cone (Tables S14–S19, ESI†), being most regular in the case of NaLMeCN⁺ species. In the case of acetonitrile adducts of LiL⁺, solvent molecule was oriented either with the nitrile group pointed towards the bulk (LiLMeCN⁺, Fig. S50a and S51a, ESI†), or oppositely (LiLMeCN'⁺, Fig. S50b and S51b, ESI†). In the latter complex, nitrile group coordinated metal cation in a similar fashion as in the lithium complex with an amide calixarene derivative where benzonitrile molecule was found to coordinate metal cation.²⁵ LiLMeCN'⁺ adduct was a result of a reorientation of specifically bound solvent molecule in the LiLMeCN⁺ complex. After the acetonitrile molecule coordinated lithium cation, it remained in that orientation for the rest of simulation. When coordinated by the MeCN nitrile group, Li⁺ cation was shifted from the binding site formed by the lower-rim substituents towards the hydrophobic cavity of L, which as an effect had a decrease of average number of coordinated nitrogen atoms, from 1.43 to 0.71 in the case of ligand 1, and from 1.01 to 0.104 in the case of lithium complex with compound 3. That made the interaction of Li⁺ and the ligands less favourable (−303 kJ mol⁻¹ for Li1MeCN′⁺ compared to −358 kJ mol⁻¹ for Li1MeCN⁺, and −294 kJ mol⁻¹ for Li3MeCN′⁺ compared to −332 kJ mol⁻¹ for Li3MeCN⁺). In addition, the absolute values of the overall interaction energies of ligands 1 and 3 with acetonitrile in LiLMeCN′⁺ complexes were lower than that in LiLMeCN⁺ species, with the difference being in the range of 80–100 kJ mol⁻¹. However, that was compensated by the interaction energy of the specifically bound acetonitrile molecule with the lithium cation (≈−130 kJ mol⁻¹ for both LiLMeCN′⁺ complexes). Furthermore, in the case of Li3MeCN′⁺, a more favourable interaction of the ligand with CH₂Cl₂ molecules compared to Li3MeCN⁺ was observed (for ≈40 kJ mol⁻¹). That could be accounted for by the fact that phenanthridine moieties in Li3MeCN′⁺ did not coordinate lithium cation, and were free to interact with the solvent molecules. The inclusion of solvent molecule in the calixarene cone enhanced the cation binding by 1 (the average number of nitrogen atoms coordinated to Li⁺ in Li1MeCN⁺ adduct is larger than in the Li1⁺ complexes, Table S14, ESI†).

A partial cation desolvation was observed in the case of Rb1MeCN⁺ and Rb1CH₂Cl₂⁺ (Fig. S55, ESI†), which had a consequence that cation–acetonitrile interaction energy was larger for these species (Table S19, ESI†) than for those where this phenomenon was not observed.

The strength of interactions of calixarene ligands with alkali-metal cations decreased as the cation size increased (Tables S14–S19, ESI†). There was just a slight difference of about 5–20 kJ mol⁻¹ in the cation–ligand interaction between Li–1⁺ and Li–3⁺, as well as between Na–1⁺ and Na–3⁺, whereby the complexes of 1 exhibited more favourable interaction. The similar interaction energies could be rationalized by the finding that, although ligand 1 possess twice more phenanthridine groups than compound 3, the steric hindrance of these groups restricted the maximum number of coordinating nitrogen atoms in the cation–calixarene complexes to 2 (Tables S14–S17, ESI†).

Solvent: methanol–dichloromethane. The structures of calixarene ligands 1 and 3 in MeOH–CH₂Cl₂ mixture was also explored by molecular dynamics simulations. During simulations, an inclusion of the methanol and dichloromethane molecules in the calixarene basket was observed (Fig. S56, ESI†). Upon that, the macrocycle hydrophobic cone became more regular than that of the free ligands (Fig. S57 and Table S12, ESI†). In the structure of LMeOH adduct, methyl group of the methanol molecule was oriented towards the calixarene lower rim, whereas the hydroxyl group pointed towards an aryl carbon atom. The binding mode of the methanol molecule in the cone was similar to that previously found in several calixarene–methanol adducts.²⁵ The inclusion of solvent molecule was more pronounced in the case of ligand 3 where 3MeOH adduct was present for 83% of the total simulation time (1MeOH was present for 47% of the simulation time). Methanol molecules were included in the baskets of 1 and 3 for much longer time than dichloromethane ones (Table S12, ESI†), which indicated that LMeOH species were more stable than LCH₂Cl₂ adducts. As in the case of MD simulations of 1 and 3 in MeCN–CH₂Cl₂ mixture, the overall interactions of dichloromethane molecules with studied macrocycles and their adducts were energetically more favourable than those corresponding to methanol molecules (Tables S13† and 2).

In the molecular dynamics simulations of alkali-metal cation complexes of 1 and sodium complex of 3 in MeOH–CH₂Cl₂ mixture, inclusion of MeOH and CH₂Cl₂ molecules in the calixarene basket was also observed, with the former process being more pronounced (Fig. S59 and S61, ESI†). Two types of methanol adducts were observed for Na–L complexes, those denoted as NaLMeOH⁺ in which solvent molecule was oriented in a similar fashion as in the LMeOH species, and adducts in which methanol molecule coordinated sodium cation by its oxygen atom (NaLMeOH′⁺). The latter ternary complex was a result of reorientation of specifically bound methanol molecule. As in the case of LiLMeCN′⁺ adducts, sodium cation was shifted towards the ether oxygen atoms which resulted in a decrease of the number of coordinated phenanthridine nitrogen atoms (Tables S20 and S21, ESI†). Again, the unfavourable effect of the coordination number decrease on complex stability was compensated by the favourable interaction of sodium cation with the solvent molecule included in the calixarene basket, with the energy of ≈−70 kJ mol⁻¹. The structural features of the other adducts, i.e. K1MeOH⁺ and Rb1MeOH⁺, were found to be similar to those of NaLMeOH⁺ complexes, except that a partial cation desolvation was observed (Fig. S64, ESI†). The cation coordination sphere consisted of ether oxygen atoms and variable number of phenanthridine nitrogen atoms (Tables S22 and S23, ESI†).

As in the MeCN–CH₂Cl₂ mixture, the absolute value of interaction energy of calixarene ligands 1 and 3 with metal ions in MeOH–CH₂Cl₂ decreased as the cation size increased (Tables S20–S23, ESI†). There was again a slight difference of about 5–20 kJ mol⁻¹ in the cation–ligand interaction energy between Na1⁺ and Na3⁺, and between the corresponding Na1–MeOH⁺ and Na3–MeOH⁺ complexes, whereby the complexes of compound 1 exhibited more favourable interaction.

Quantum chemical calculations

In order to get a more detailed insight into the possible structures of the receptor 1 complexes with alkali-metal cations, the extensive search of the corresponding conformational space was carried out. The initial set of geometries was obtained by the analysis of PES calculated at the semiempirical level of the theory (PM6). PES was spanned in the space of 8 torsional coordinates (Scheme 1) and then parallelized optimization procedure for finding local minima utilizing a brute-force search in n-way space was applied resulting in 425 local minima. Each of these minima was subsequently optimized using density functional theory. To ensure that optimized structures indeed corresponded to local minima, harmonic frequency calculations were carried out and normal modes were examined. Additional clustering of the optimized geometries provided an estimate of the conformational space of 1 with more than one hundred conformers. The most interesting conformers from the structural end energetic points of view were optimized using the B3LYP/6-31G(d) method with D3 version of Grimme's dispersion and Becke–Johnson damping.⁴⁴ These conformers are presented herein in order of descending coordination number (number of oxygen and nitrogen atoms that coordinate cation). Conformers with the coordination number 8 and maximal possible symmetry (C₄) for complexes of 1 with Li⁺, Na⁺, and K⁺ are presented in Fig. 8.

Fig. 8 Conformer with the coordination number 8 (C₄ point group): complex of 1 with Li⁺ (white), with Na⁺ (yellow), and with K⁺ (purple). The hydrogen atoms are omitted for clarity.

The position of the cation inside the calixarene binding site is determined by the size of the metal ion. Lithium cation is positioned nearly in the plane defined by the oxygen atoms whereas the Na⁺ and K⁺ are shifted from this position by 0.560 Å and 1.492 Å, respectively. These changes in position were accompanied by the small outward shifts of oxygen atoms and small inward shifts of nitrogen atoms of the phenanthridine groups.

The next interesting conformer with the coordination number 7 is presented in Fig. S65, ESI.† In this conformer nitrogen atoms from three phenanthridine units make a triangle around the cation whose position is shifted to some extent from the centerline of the molecule.

In the conformer with the coordination number 6 phenanthridine subunits are stacked in pairs with two units coordinating the cation by their nitrogen atoms (Fig. S66, ESI†).

In the conformer with the coordination number 5 the cation is slightly shifted from the molecule centerline, and three phenanthridine units are stacked whereas the remaining unit interacts with the central phenanthridine moiety in a T-shape manner (Fig. S67, ESI†).

The cation position in the conformer with the coordination number 4 is at the molecule centerline (Fig. S68, ESI†). The phenanthridine units are arranged in a T-shape conformation, all of them surrounding the cations with their π-systems.

As the extensive inclusion of the acetonitrile molecule in the hydrophobic cavity of compound 1 was observed by MD simulations, DFT calculations of the corresponding structures were carried out. It is interesting to note how the orientation of the included MeCN molecule depends on the cation complexed (Fig. 9). The DFT optimized structure of the ternary complex Li1MeCN'⁺ in which Li⁺ is coordinated by the solvent nitrile group is shown in Fig. 10. In this species lithium cation is slightly shifted from the cation-binding site formed by the lower-rim substituents toward the hydrophobic cavity of 1 compared to its position in the structures without coordinating acetonitrile molecule.

Fig. 9 Conformer with the coordination number 8 (C₁ point group): complex of 1 with Li⁺ (white), with Na⁺ (yellow), and with K⁺ (purple) and one acetonitrile molecule. The hydrogen atoms of the calixarene unit are omitted for clarity.

Fig. 10 Conformer with the coordination number 8: complex of 1 with Li⁺ (white) and one acetonitrile molecule. The hydrogen atoms of the calixarene unit are omitted for clarity.

Conclusions

The comprehensive thermodynamic and computational studies of the alkali-metal cations binding with three new phenanthridine-based calix[4]arene derivatives were carried out in order to get as detailed as possible insight into the corresponding complexation reactions. The solvent effect on these processes was addressed as well. The fluorescence of compounds 1 and 3 was shown to be considerably influenced by metal-ion binding which makes them candidates for highly sensitive cation sensors. The stability constants of the M1⁺, M2⁺, and M3⁺ complexes were determined by means of fluorimetric, spectrophotometric, potentiometric, and microcalorimetric titrations. The latter technique also provided information on reaction enthalpies and entropies.

Tetra-phenanthridine derivative 1 was found to be a quite good binder of all investigated cations (except of the largest Cs⁺) in both MeCN–CH₂Cl₂ and MeOH–CH₂Cl₂ solvent mixtures. As expected due to the difference in acetonitrile and methanol solvation abilities, the complex stabilities were much higher in the former solvent, with a rather pronounced selectivity peak corresponding to sodium cation (Tables 1 and 2). The calorimetric investigations of the compound 1 binding abilities revealed that this is predominantly due to the most favourable complexation enthalpy of sodium cation in comparison with other alkali-metal cations. The affinities of compounds 2 and 3 towards alkali-metal ions were found to be much lower compared to those of 1, which can be, at least partly, rationalized by taking into account larger number of possible coordinating sites in the latter ligand. Somewhat surprisingly, the enthalpy of lithium complexation by ligand 3 was more negative than that by 1, and the sodium binding with both compounds 1 and 3 resulted with almost identical complexation enthalpies. On the contrary, the standard reaction entropies of Li⁺ and Na⁺ complexation with macrocycle 1 were notably more favourable than those with 3. The NMR investigations suggested that such large differences in the Δ_rS° values for sodium and lithium binding with the examined ligands could be attributed to the presence of several conformers in solution of compound 3, whereas the ligand 1 adopted the cone conformation. The ligand 1 is hence better suited for cation complexation because of the proper orientation of its binding sites at the lower rim. However, the ligand 3 was shown to bind Li⁺ and Na⁺ rather good in MeCN–CH₂Cl₂. The stability of lithium complex was slightly higher than that of sodium, as a result of more favourable complexation entropy. That could be, partly, explained by the higher desolvation entropy of lithium cation. As already stated, the stabilities of alkali-metal cation complexes with the investigated ligands were much lower in MeOH–CH₂Cl₂ as compared to MeCN–CH₂Cl₂ solvent mixture. Such differences in the ligand binding abilities in the solvents examined could be rationalized by taking into account the differences in the cation solvation in methanol and acetonitrile, and by the tendency for the inclusion of solvent molecules into the hydrophobic cavity of the macrocycles. Namely, during the MD simulations of alkali-metal salt solutions, the preferential solvation of cations with either methanol or acetonitrile with respect to dichloromethane was noticed. The strongly favourable cation standard transfer Gibbs energies from CH₂Cl₂ to both MeCN and MeOH strongly support the computational results. Likewise, the MD simulations indicated the preferential inclusion of MeCN molecule in the lipophylic cavity of both macrocycles which was previously proven to play an important role in the enthalpic stabilization of the metal–ion complexes formed.

To shed more light on the possible structures of the ligand 1 and its complexes with alkali-metal cations, besides MD simulations, the detailed search of the conformational space was undertaken on the semiempirical level, followed by the DFT optimization of the local-minima-corresponding structures. Several energetically and structurally most interesting conformers are outlined.

The results presented in this paper clearly indicate how remarkable and complex the influence of the solvent on the ion-hosting abilities of the calixarene derivatives and macrocycles in general can be. They also suggest that integrated and comprehensive experimental and computational investigations could provide a detail insight into the ligand properties and reactivities, which can serve as a basis for targeted design of efficient and selective supramolecular receptors.

Experimental

Syntheses

General. All reagents used in the syntheses were of the best grade commercially available and were used without further purification. Solvents were purified by standard procedures.⁴⁵ Reaction course and purity of the products were checked by thin-layer chromatography (TLC) on Merck, DC-Alufolien Kieselgel 60 F254, using 5% dichloromethane–methanol mixture as eluent. Melting points were determined with a Kofler apparatus. ¹H NMR and ¹³C NMR spectra were recorded on a Bruker Avance AV300 or AV600 MHz spectrometer with (CH₃)₄Si as an internal standard. COSY and NOESY spectra were recorded to enable a complete assignment of signals. IR spectra were recorded by means of an ABB Bomem MB102 FTIR spectrometer. Mass spectrometry (MS) measurements were conducted on a 4800 MALDI TOF/TOF Analyzer, Applied Biosystems mass spectrometer. Compounds 6-(chloromethyl)phenanthridine^46,47 and dimethoxy-p-tert-butylcalix[4]arene⁴⁸ were prepared as described earlier.

5,11,17,23-Tetra-tert-butyl-25,26,27,28-tetrakis-((phenanthridine-6-yl)methoxy)calix[4]arene (1) and 5,11,17,23-tetra-tert-butyl-25,27-bis-((phenanthridine-6-yl)methoxy)-26,28-dihydroxycalix[4]arene (2). In 25 cm³ of anhydrous acetone, 0.635 g of 5,11,17,23-tetra-tert-buthyl-25,26,27,28-tetrahydroxicalix[4]arene (0.98 mmol) and 5.412 g of potassium carbonate (39.15 mmol) were suspended and stirred for about an hour at room temperature in argon atmosphere. Then, 1.783 g of 6-(chloromethyl)phenanthridine^46,47 (7.83 mmol, 100% excess per group) and 1.300 g of potassium iodide (7.83 mmol) were added to the reaction mixture and stirred for additional 8 hours under argon, and another 48 hours at room temperature, protected from the daylight. Reaction mixture was filtered, the residue was washed with dichloromethane and the combined filtrate was collected and evaporated by vacuum. The residue was dissolved in dichloromethane, extracted with water, evaporated to dryness and then triturated with anhydrous methanol which gave whitish precipitate. The precipitate was recrystallized from acetonitrile to give compound 1 (1.192 g; 43% yield). When the same procedure was carried out using smaller amounts of 6-(chloromethyl)phenanthridine (1 equivalent per reactive group of calix[4]arene) compound 2 was obtained as the major product (63% yield).

Compound 2 was also prepared by microwave assisted synthesis. In 25 cm³ of anhydrous acetone, 0.250 g of 5,11,17,23-tetra-tert-buthyl-25,26,27,28-tetrahydroxicalix[4]arene (0.39 mmol) and 1.597 g of potassium carbonate (11.56 mmol) were suspended and stirred for about an hour at room temperature in argon atmosphere. Then, 0.193 g of 6-(chloromethyl)phenanthridine (0.85 mmol) and 0.256 g of potassium iodide (1.54 mmol) were added to the reaction mixture and stirred for 2.5 hours at 82 °C while exposed to microwave radiation. Reaction mixture was filtered and evaporated of the organic solvent, extracted in dichloromethane/water. The residue was triturated with anhydrous ethanol which gave whitish precipitate. The crude product was recrystallized from absolute ethanol to give 0.378 g of compound 2 (88% yield).

The analytical data for compounds 1 nad 2 are given in ESI.†

5,11,17,23-Tetra-tert-butyl-25,27-bis-((phenanthridine-6-yl)methoxy)-26,28-dimethoxycalix[4]arene (3). 0.789 g (1.17 mmol) of 5,11,17,23-tetra-tert-buthyl-25,27-dihydroxi-26,28-dimethoxycalix[4]arene (prepared according to the literature procedures⁴⁸) and 0.117 g of 80% suspension of NaH in paraffin oil were added to 40 cm³ of anhydrous dimethylformamide and stirred for 5 minutes on ice bath, and then for additional 30 minutes at room temperature. Then, 1.100 g of 6-(chloromethyl)phenanthridine (4.83 mmol) was added to reaction mixture and stirred for 1 hour on ice bath, and then for another 4 days at room temperature. A few drops of water were added to the reaction mixture and most of the solvent was then removed under reduced pressure. The residue was dissolved in dichloromethane and salts were filtered off, and solvent was evaporated to dryness. Crude product was recrystallized from acetonitrile to give 0.824 g of precipitate (compound 3) with 67% yield.

The analytical data for compound 3 are given in ESI.†

Physicochemical measurements

Materials. The salts used for the investigation of 1, 2, and 3 complexation were LiClO₄ × H₂O (Fluka, p.a. and Sigma Aldrich, 99.99%), NaClO₄ × 3H₂O (Fluka, p.a.), NaClO₄ (Sigma Aldrich, 98+%), KClO₄ (Merck, p.a.), RbNO₃ (Sigma, 99.7%) and CsNO₃ (Sigma, 99.5%). The solvents, acetonitrile (Merck, Uvasol) and methanol (Merck, Uvasol), were used without further purification, whereas dichloromethane (Fluka, Merck) was distilled twice. Ionic strength was kept constant at 0.01 mol dm⁻³ by addition of Et₄NClO₄ (Fluka, p.a.).

Conductometry. The ion-association constants in MeCN–CH₂Cl₂ and MeOH–CH₂Cl₂ solvent mixture were determined conductometrically. The maximum tested concentration was limited by the condition that no triple ions should appear.⁴⁹

Measurements were performed at (25.0 ± 0.1) °C using a dipping type conductivity cell Orion 018001 with two electrodes of bright platinum. The cell constant (0.10402 ± 0.00002 cm⁻¹) was determined by calibration with aqueous potassium chloride solutions in the concentration range from 0.001 to 0.05 mol dm⁻³. The conductivity cell was connected to a precision component analyser Wayne-Kerr (model 6430A). The resistance (R) of the test solutions was measured at four frequencies: f = 500, 800, 1000 and 2000 Hz. Its dependence on reciprocal frequency was well presented by a straight line and the intercept (R₀) was obtained by the least-squares method.

The experimental procedure began by weighing the pure solvent into a glass reaction cell. The reaction cell was then hermetically closed with a teflon lid and placed into a Thermo-Haake Circulator DC10-V15/B which maintained the temperature at (25.00 ± 0.01) °C. After achievement of thermal equilibrium, the resistances at four frequencies were determined. Then, the known weight of stock solution was added into the cell using a syringe, and the resistance readings repeated. Between these two operations the test solution was homogenized through a short-run spin of a teflon magnetic stirr bar activated by an immersible stirrer Cyclone (model 1–100 HMC).

The conductance data were analysed by the Lee-Wheaton conductance equation in Pethybridge and Taba version (LWPT model),⁴¹ and the limiting molar conductivities (Λ₀) as well as ion-association equilibrium constants (K_A) were determined.

Spectrophotometry and fluorimetry. UV titrations were performed by means of a Varian Cary 5 double-beam spectrophotometer whereas fluorimetric measurements were carried out using a PekinElmer LS-55 spectrofluorimeter, both equipped with a thermostatting device. UV and fluorescence spectra were recorded at 0.5 nm intervals at (25.0 ± 0.1) °C using 1 cm optical path length quartz cells. Spectral changes of solutions of 1, 2 or 3 were recorded upon stepwise additions of an alkali-metal salt solution directly into the measuring cell. Absorbances were sampled with integration time of 0.2 s, whereas fluorescence intensities were collected with scanning speed of 600 nm min⁻¹. Titrations for each M⁺/L system (M⁺ stands for alkali-metal cation and L denotes 1, 2 or 3) were done in triplicate. The obtained data were processed using the SPECFIT⁵⁰ and HYPERQUAD⁵¹ programs. In the course of spectrophotometric and spectrofluorimetric determinations of stability constants, ion-association was taken into account.

Potentiometry. For potentiometric measurements, Metrohm 713 pH meter was used. Titrations were carried out in thermostatted vessel at (25.0 ± 0.1) °C, and the ionic strength of all solutions was kept at 0.01 mol dm⁻³ by addition of Et₄NClO₄. The indicator electrode was a sodium-selective glass electrode (Metrohm, 6.0501.100) with Ag/AgCl reference electrode (Metrohm, 6.0733.100) filled with MeCN–CH₂Cl₂ solution of Et₄NCl (c = 0.01 mol dm⁻³). The working and reference half-cells were connected with a salt bridge containing 0.01 mol dm⁻³ Et₄NClO₄. The cell was calibrated by the incremental addition of NaClO₄ solution (c = 9.94 × 10⁻³ mol dm⁻³) to 30.0 cm³ solution of Et₄NClO₄ (c = 0.01 mol dm⁻³) in MeCN–CH₂Cl₂ mixture (φ = 0.5). In each calibration experiment a Nernst-like behavior was observed, with the slope of E vs. p[Na] plot being about −58 mV.

Stability constants of Na1⁺ and Na3⁺ complexes in MeCN–CH₂Cl₂ mixture were determined by potentiometric titration of NaClO₄ solution (V = 30 cm³) with solution of 1 and 3, respectively. Titrations were repeated three times, and the obtained potentiometric data were analyzed with the HYPERQUAD program.⁵¹

Calorimetry. Microcalorimetric measurements were performed by an isothermal titration calorimeter Microcal VP-ITC at 25.0 °C. In the calorimetric titrations, the enthalpy changes obtained upon stepwise, automatic addition of alkali-metal to solutions of 1 and 3 (c = 1 × 10⁻⁴ mol dm⁻³ to 2 × 10⁻⁴ mol dm⁻³) were recorded. Due to the instrument sensitivity, quite dilute titrans solutions were used. The anions of alkali-metal salts were either tetraphenylborates or perchlorates, i.e. large ions with the low charge density and the low tendency for ion-pairing. In this way the extent of latter process in the calorimetric cell was significantly reduced or even almost completely eliminated. Namely, after the titrant dilution in pure solvent, only a few percent of ions remained associated (5% at most). For that reason, the contribution of ion-pair dissociation to the recorded enthalpy changes and its influence on the complexation equilibrium could be neglected in all cases. Heats corresponding to dilution of salt solutions were obtained by blank experiments, and subtracted from those measured in the titration experiment. The dependence of successive enthalpy change on the titrans volume was processed by nonlinear least-square fitting procedure using ORIGINPRO 7.0 program. Titrations for each cation/ligand system were repeated three times.

The calorimeter reliability was checked by carrying out the complexation of barium(II) by 18-crown-6 in aqueous medium at 25 °C. The results obtained log K = 3.76, Δ_rH = −30.9 kJ mol⁻¹) were in good agreement with the literature values (log K = 3.73, Δ_rH = −31.5 kJ mol⁻¹).⁵²

Molecular dynamics simulations. The molecular dynamics simulations were carried out by means of the GROMACS⁵³ package (version 4.6.5). Intramolecular and nonbonded intermolecular interactions in calixarene ligands and in acetonitrile molecules were modelled by the OPLS-AA (Optimized Parameters for Liquid Simulations-All Atoms) force field.⁵⁴ Partial charges assigned to ring carbons bound to CH₂ groups that link the monomers were assumed to be zero as described in ref. 55. Partial charges of phenanthridine atoms where calculated for a model compound of 6-ethylphenanthridine with Gaussian 09 software at HF/6-31+G level of theory using a CHelpG scheme.⁵⁶ The initial structures of free ligands were those in which the calixarene basket had a conformation of a flattened cone. Bond stretching and angle bending parameters for CH₂Cl₂ molecule were taken from ref. 57. The initial structures of calixarene complexes were made by placing a cation in the center of lower-rim cavity between ether oxygen atoms and nitrogen atoms of phenanthridine substituents. The M1⁺ and M2⁺ species (M⁺ denotes alkali metal cation) were solvated in a cubical box (edge length 56 Å) of MeCN–CH₂Cl₂ or MeOH–CH₂Cl₂ mixture with periodic boundary conditions. The number ratio of solvent molecule types in these boxes was similar to that found in solvent mixture obtained by mixing the equal volumes of mixture components. The solvent mixture boxes where equilibrated prior to solvation of calixarene ligands and their complexes. The solute concentration in such boxes was about 0.01 mol dm⁻³. During the simulations of the systems, ClO₄⁻ ion was included to neutralize the box. The perchlorate counterion was held fixed at the box periphery whereas the complex was initially positioned at the box center. In all simulations an energy minimization procedure was performed followed by a molecular dynamics simulation in NpT conditions for 55 ns, where first 0.5 ns were not used in the data analysis. Whenever an association of calixarene complex with perchlorate anion was observed, the corresponding data were discarded and more simulations were performed in order to bring the total simulation time to about 50 ns. The Verlet algorithm⁵⁸ with a time step of 1 fs was employed. The cutoff radius for nonbonded van der Waals and short-range Coulomb interactions was 16 Å. Long-range Coulomb interactions were treated by the Ewald method as implemented in the PME (Particle Mesh Ewald) procedure.^59,60 The simulation temperature was kept at 298.15 with Nosé–Hoover^61,62 algorithm using a time constant of 1 ps. The pressure was kept at 1 bar by Martyna–Tuckerman–Tobias–Klein⁶³ algorithm and a time constant of 1 ps.

Quantum chemical calculations. Conformational search for compound 1 was performed by calculation of complete potential energy surface (PES). PES was spanned by 8 relevant torsional coordinates φ₁–φ₈. Torsional coordinates φ₁, φ₃, φ₅ and φ₇ were investigated in the relative range of 0–360° whereas the torsional coordinates φ₂, φ₄, φ₆ and φ₈ were explored in the relative range 0–120° starting from the initial structure. PES scans were obtained by varying the torsional coordinates using the automatic conformational generator implemented in program qcc.^64,65 A total number of 2 313 441 single point calculation were conducted at the PM6 semiempirical level of the theory.⁶⁶

Data from PES scans were arranged in an eight-way array. Parallelized combinatorial optimization algorithm for the arbitrary number of ways (dimensions) implemented in program moonee⁶⁷ was used to determine all local minima on the investigated PES. All local minima were reoptimized at the B3LYP/3-21G level of the theory. To ensure that the obtained geometries indeed corresponded to local minima, harmonic frequency calculations were performed. All quantum-chemical calculations were performed using the Gaussian 09 program.⁵⁶

Notes and references

1. V. Böhmer, Angew. Chem., Int. Ed., 1995, 34, 713–745.
2. B. S. Creaven, D. F. Donlon and J. McGinley, Coord. Chem. Rev., 2009, 253, 893–962.
3. D. C. Gutsche, in Calixarenes: An Introduction (Monographs in Supramolecular Chemistry), ed. J. F. Stoddard, RSC Publishing, Cambridge, 2nd edn, 2008.
4. Y. K. Agrawal, J. P. Pancholi and J. M. Vyas, J. Sci. Ind. Res., 2009, 68, 745–768.
5. P. Jose and S. Menon, Bioinorg. Chem. Appl., 2007, 2007, 65815.
6. G. McMahon, S. O'Malley, K. Nolan and D. Diamond, ARKIVOC, 2003, 2003, 23–31.
7. W. Śliwa, J. Incl. Phenom. Macrocycl. Chem., 2005, 52, 13–37.
8. A. F. Danil de Namor and M. Shehab, J. Phys. Chem. B, 2005, 109, 17440–17444.
9. R. Dorta, L. J. W. Shimon, H. Rozenberg, Y. Ben-David and D. Milstein, Inorg. Chem., 2003, 42, 3160–3167.
10. Y. Molard and H. Parrot-Lopez, Tetrahedron Lett., 2002, 43, 6355–6358.
11. K. Shimojo and M. Goto, Anal. Chem., 2004, 76, 5039–5044.
12. J.-O. Dalbavie, J.-B. Regnouf-de-Vains, R. Lamartine, M. Perrin, S. Lecocq and B. Fenet, Eur. J. Inorg. Chem., 2002, 2002, 901–909.
13. O. Sénèque, M. Campion, B. Douziech, M. Giorgi, Y. Le Mest and O. Reinaud, Dalton Trans., 2003, 4216–4218.
14. O. Sénèque, M. Campion, M. Giorgi, Y. Le Mest and O. Reinaud, Eur. J. Inorg. Chem., 2004, 1817–1826.
15. P. Molenveld, J. F. J. Engbersen and D. N. Reinhoudt, J. Org. Chem., 1999, 64, 6337–6341.
16. Y.-D. Cao, Q.-Y. Zheng, C.-F. Chen, H.-M. Hu and Z.-T. Huang, Inorg. Chim. Acta, 2004, 357, 316–320.
17. A. F. Danil de Namor, Coord. Chem. Rev., 1999, 190–192, 283–295.
18. H. Li, J. Zhan, M. Chen, D. Tian and Z. Zou, J. Inclusion Phenom. Macrocyclic Chem., 2009, 66, 43–47.
19. A. F. Danil De Namor, R. M. Cleverley and M. L. Zapata-Ormachea, Chem. Rev., 1998, 98, 2495–2526.
20. V. Tomišić, N. Galić, B. Bertoša, L. Frkanec, V. Simeon and M. Žinić, J. Inclusion Phenom. Macrocyclic Chem., 2005, 53, 263–268.
21. A. F. Danil De Namor, R. G. Hutcherson, F. J. Sueros Velarde, M. L. Zapata-Ormachea, L. E. Pulcha Salazar, I. Al Jammaz and N. Al Rawi, Pure Appl. Chem., 1998, 70, 769–778.
22. J. Požar, T. Preočanin, L. Frkanec and V. Tomišić, J. Solution Chem., 2010, 39, 835–848.
23. G. Horvat, V. Stilinović, T. Hrenar, B. Kaitner, L. Frkanec and V. Tomišić, Inorg. Chem., 2012, 51, 6264–6278.
24. J. Požar, G. Horvat, M. Čalogović, N. Galić, L. Frkanec and V. Tomišić, Croat. Chem. Acta, 2012, 85, 541–552.
25. G. Horvat, V. Stilinović, B. Kaitner, L. Frkanec and V. Tomišić, Inorg. Chem., 2013, 52, 12702–12712.
26. A. F. Danil de Namor, D. Kowalska, E. E. Castellano, O. E. Piro, F. J. Sueros Velarde and J. Villanueva Salasa, Phys. Chem. Chem. Phys., 2001, 3, 4010–4021.
27. J. S. Kim and D. T. Quang, Chem. Rev., 2007, 107, 3780–3799.
28. N. Galić, N. Burić, R. Tomaš, L. Frkanec and V. Tomišić, Supramol. Chem., 2011, 23, 389–397.
29. M. Kumar, J. N. Babu, V. Bhalla and R. Kumar, Sens. Actuators, B, 2010, 144, 183–191.
30. Calixarenes in the Nanoworld, ed. J. Vicens, J. Harrowfield and L. Baklouti, Springer, 2007.
31. B. Valeur and I. Leray, Inorg. Chim. Acta, 2007, 360, 765–774.
32. K. K. Sadhu, S. Sen and P. K. Bharadwaj, Dalton Trans., 2011, 40, 726–734.
33. G. Qing, Y. He, F. Wang, H. Qin, C. Hu and X. Yang, Eur. J. Org. Chem., 2007, 2007, 1768–1778.
34. S. Alihodžić, M. Žinić, B. Klaić, R. Kiralj, B. Kojić-Prodić, M. Herceg and Z. Cimerman, Tetrahedron Lett., 1993, 34, 8345–8348.
35. R. Kiralj, B. Kojić-Prodić, M. Žinić, S. Alihodžić and N. Trinajstić, Acta Crystallogr., Sect. B: Struct. Sci., 1996, 52, 823–837.
36. S. Alihodžić and M. Žinić, Croat. Chem. Acta, 1999, 72, 803–817.
37. L. Frkanec, A. Višnjevac, B. Kojic and M. Žinić, Chem.–Eur. J., 2000, 6, 442–453.
38. N. M. Buie, V. S. Talanov, R. J. Butcher and G. G. Talanova, Inorg. Chem., 2008, 47, 3549–3558.
39. A. F. Danil De Namor, M. C. Cabaleiro, B. M. Vuano, M. Salomon, O. I. Pieroni, D. A. Pacheco Tanaka, C. Y. Ng, M. A. Llosa Tanco, N. M. Rodrfguezz, J. D. Cardenas Garcia and A. R. Casal, Pure Appl. Chem., 1994, 66, 435–440.
40. N. G. Tsierkezos, J. Mol. Liq., 2008, 138, 1–8.
41. A. D. Pethybridge and S. S. Taba, J. Chem. Soc., Faraday Trans. 1, 1980, 76, 368–376.
42. B. Valeur, Molecular Fluorescence: Principles and Applications, WILEY-VCH, Weinheim, 2001.
43. Y. Marcus, Ion Properties, CRC Press, Boca Raton, FL, 1997.
44. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
45. W. L. F. Armarego and C. L. L. Chai, Purification of Laboratory Chemicals, Elsevier, Burlington, 6th edn, 2009.
46. G. T. Morgan and L. P. Walls, J. Chem. Soc., 1931, 2447–2456.
47. E. C. Taylor and N. W. Kalenda, J. Am. Chem. Soc., 1954, 76, 1699–1700.
48. P. J. Dijkstra, J. A. J. Brunink, K. E. Bugge, D. N. Reinhoudt, S. Harkema, R. Ungaro, F. Ugozzoli and E. Ghidini, J. Am. Chem. Soc., 1989, 111, 7567–7575.
49. R. M. Fuoss and F. Accascina, Electrolyte Conductance, Interscience, New York, 1959.
50. G. A. Kriss, in Astronomical Data Analysis Software & Systems III, A.S.P. Conf. Series, ed. D. R. Crabtree, R. J. Hanisch and J. Barnes, Astronomical Society of the Pacific, San Francisco, 1994, vol. 61, p. 437.
51. P. Gans, A. Sabatini and A. Vacca, Talanta, 1996, 43, 1739–1753.
52. J. Tellinghuisen, J. Phys. Chem. B, 2007, 111, 11531–11537.
53. B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447.
54. W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236.
55. A. S. de Araujo, O. E. Piro, E. E. Castellano and A. F. Danil de Namor, J. Phys. Chem. A, 2008, 112, 11885–11894.
56. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, M. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz and J. Cioslowski, Gaussian 09, Revision D.01, Gaussian Inc., Wallingford CT, 2013.
57. L. X. Dang, J. Phys. Chem. B, 2001, 105, 804–809.
58. W. C. Swope, H. C. Andersen, P. H. Berens and K. R. Wilson, J. Chem. Phys., 1982, 76, 637–649.
59. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092.
60. U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593.
61. S. Nosé, Mol. Phys., 1984, 52, 255–268.
62. W. Hoover, Phys. Rev. A, 1985, 31, 1695–1697.
63. G. J. Martyna, M. E. Tuckerman, D. J. Tobias and M. L. Klein, Mol. Phys., 1996, 87, 1117–1157.
64. T. Hrenar, qcc, Quantum Chemistry Code, rev. 0.68, 2014.
65. I. Primožič, T. Hrenar, K. Baumann, L. Krišto, I. Križić and S. Tomić, Croat. Chem. Acta, 2014, 87, 153–160.
66. J. J. P. Stewart, J. Mol. Model., 2007, 13, 1173–1213.
67. T. Hrenar, moonee, Code for Manipulation and Analysis of Multi- and Univariate Data, rev. 0.6826, 2014.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental and computational procedures: syntheses of compounds 1–3 and the corresponding analytical data; conductometric measurements, spectrophotometric, fluorimetric, NMR, potentiometric, and calorimetric titrations; molecular dynamics, and density functional theory. The results obtained by MD simulations. Additional results of the ion-association investigation, titration experiments and DFT calculations. See DOI: 10.1039/c5ra01905b

---