Fabrication of asymmetric-gradient-concentric ring patterns via evaporation of droplets of PMMA solution at different substrate temperatures

Abstract

Gradient-concentric ring patterns were constructed via the evaporation of droplets of PMMA–toluene solution at different substrate temperatures, using a copper ring to control the evaporative behavior of the droplets and the motion of the contact line. The wavelength and amplitude of the concentric rings were found to decrease with the decrease of the distance to the copper ring. Curvature-induced asymmetry of the surface patterns with respect to the copper ring was observed. The geometric characteristics of the concentric rings were dependent on the solution concentration and the substrate temperature. Higher substrate temperature led to the formation of concentric rings of larger wavelengths and smaller ratio of the amplitude to the wavelength for the inner concentric rings. Microscale structures were observed in the trenches between two adjacent polymer ridges, which changed with the wavelength of the concentric rings and the substrate temperature.

---

Introduction

Well-ordered surface structures, especially those in the micro and nano scales, have potential in various application areas, including electronics,¹ photonics,² surface adhesion,³ tissue engineering,⁴ biomedical devices,^5,6 etc. Various techniques have been developed to fabricate well-ordered surface structures,^7–12 while it is still a great challenge to construct highly-ordered surface structures efficiently and economically. Evaporation-induced surface patterning is an economy-effective method to construct surface patterns. The principle behind the evaporating-induced surface patterning is the “coffee-ring” behavior.¹³ When a droplet of a polymer solution or a particle suspension evaporates on a substrate, the non-volatile solute tends to deposit in the vicinity of the contact line as the contact line is pinned.¹⁴ Several templates have been developed to fabricate well-ordered surface structures via controlling the evaporation of a solution droplet and the motion of the contact line. Concentric rings with gradients of wavelengths and amplitudes were constructed by confining the evaporation of a solution droplet within a “sphere-on-flat” geometry.^15,16 Gradient straight stripes also were fabricated by replacing a spherical lens with a wedge or a cylinder.^17,18 Straight stripes of uniform wavelength were produced by confining a polymer solution film within two parallel glass plates and using a computer system to control the motion of the top glass plate.¹⁹ A “roll-based” system was developed to fabricate parallel stripes over a large area.²⁰ Various materials have been used to construct surface patterns via the evaporation-induced surface patterning, such as homopolymer,²¹ polymer blend,²² block copolymer,²³ nanoparticles,¹⁸ carbon nanowire,²⁴ graphene,²⁰ DNA,²⁵ etc. All of these works demonstrate the potential to meet the requirement of different fields.

To better control the characteristics of surface patterns and understand the formation mechanisms, several effects have been investigated, i.e. solution concentration,^16,26 droplet size,²⁷ solvent,²⁸ affinity between solute and substrate,²⁹ curvature of contact line,^13,30 etc. Temperature, which determines the evaporation rate, viscosity and micro-flows inside a droplet, is another important factor. However, there are only limited studies investigating the temperature effect on the evaporation-induced patterns. Bodiguel et al.³¹ studied the temperature effect on the pinning and depinning force for the “stick–slip” motion of a liquid film sandwiched between two glass plates. Uchiyama et al.³² fabricated surface-patterned hybrid films by combining sol–gel process with dip-coating process. They found that the dimensions of the parallel stripe patterns were enlarged significantly when increasing the dip-coating temperature. However, none of these studies has constructed asymmetric-gradient-concentric ring patterns from polymer solutions and examined the microscale structures between adjacent rings or stripes, which likely limit the applications of the surface patterns.

In this study, we fabricate concentric ring-like patterns with asymmetric gradients, using a simple copper ring to confine the evaporation of a droplet of polymer solution. Well-ordered patterns are formed both inside and outside the copper ring, while the characteristics of the patterns inside and outside the copper rings are different due to the curvature effect. The effects of the solution concentration and the substrate temperature on the characteristics of the surface patterns are examined, and the structures formed in the trenches between two adjacent rings are also analyzed.

Results and discussion

Fig. 1 shows typical optical images of the surface patterns formed via the evaporation of a droplet of PMMA–toluene solution with a concentration of 0.25 wt%, using a copper ring of 1380 μm in diameter. From Fig. 1a, one can observe that concentric ring-like patterns were formed both inside and outside the copper ring with an approximately circular-featureless zone in the center. Less regular rings interconnecting with neighbors by “branches” are found outside the copper ring, and the concentric rings inside the copper ring are well ordered. The wavelength of the concentric rings (distance between the centers of adjacent rings) gradually decreases as the PMMA rings approach to the copper ring for both the patterns inside and outside the copper ring. The wavelength gradient is more clearly revealed in Fig. 1b and c. The gradient-circular pattern related to the copper ring is not symmetric. For approximately the same distance to the copper ring, the concentric rings inside the copper ring (Fig. 1b) exhibit larger wavelengths than the corresponding concentric rings outside the copper ring (Fig. 1c).

Fig. 1 Typical optical images of the concentric rings formed with a copper ring via the evaporation of a droplet of PMMA solution (copper ring diameter: 1380 μm, solution concentration: 0.25 wt%, substrate temperature: 21 °C). (a) A large view of the surface pattern, (b) an enlarged view of the concentric rings near the copper ring formed outside the copper ring, (c) an enlarged view of the concentric rings near the copper ring formed inside the copper ring, and (d) schematic of the formation of the PMMA rings. P, W and V represent pinning (stick), wavelength and volume change during the stick–slip motion of the contact line, respectively.

The concentric rings outside the copper ring were formed due to the typical “stick–slip” motion of the contact line outside the copper ring.^22,33 The motion of the contact line can be considered as the result of the resultant force exerted on the contact line. When the resultant tangential component of surface tensions is equal to the local friction on the contact line, the contact line is pinned, i.e. the contact line is at “stick” state. With the contact line being pinned, the non-volatile PMMA accumulates in the vicinity of the contact line and forms a circular ridge. During the pinning, the solvent continuously evaporates and the nominal contact angle decreases. This leads to the increase of the resultant tangential component of surface tension acting on the copper ring. When the friction is unbalanced by the resultant tangential component of surface tension, the contact line starts to move towards the copper ring again to the next pinning state due to the increase of the contact angle.³⁵ The repeated “stick–slip” motion of the contact line results in the formation of the concentric ring patterns.

After placing a droplet on the glass slide, the evaporation of toluene and the confinement of the copper ring led to the occurring of dewetting of the solution droplet and the formation of an internal contact line near the center of the ring when the droplet inside the copper ring reached a critical volume.²⁹ The internal dewetting front (the internal contact line newly formed) first receded smoothly to the copper ring until it was pinned. The first pinning produced the smallest internal PMMA ring and formed a featureless zone in the center of the copper ring. Note that the system in this study is different from the “copper ring-on-film” system,³⁰ in which the patterns were formed due to the flow of the soft, flowable layer between softened pre-cast film and toluene. Here the PMMA was deposited from the solution. The difference of the mechanisms in the pattern formation can also be revealed from the comparison of the formed micro-patterns, as discussed late.

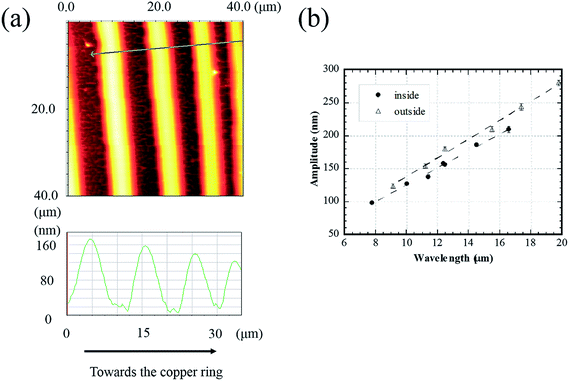
Fig. 2a shows an AFM image of the concentric rings formed inside a 3750 μm copper ring. The solution concentration was 0.125 wt% PMMA. Locally, the segments of the concentric rings appear parallel. By drawing a line perpendicular to the segments, as shown in Fig. 2a, the wavelength and amplitude of the concentric rings can be determined. From the line scan in Fig. 2a, one notes that both the wavelength and amplitude gradually decreases as the concentric rings approach to the copper ring. Fig. 2b shows the variation of the amplitude with the wavelength of the concentric rings inside and outside a 3750 μm copper ring for the droplets with a concentration of 0.125 wt% PMMA. The amplitude increases linearly with the increase of the wavelength for both the concentric rings inside and outside the copper ring. The amplitude of a concentric ring is mainly determined by the amount of the non-volatile PMMA deposited at the “stick” state, which can be approximately evaluated by the volume loss of the droplet between two adjacent “stick” states. As schematically illustrated in Fig. 1d, P, W and V represent pinning (stick), wavelength and volume change during the stick–slip motion of the contact line, respectively. For two adjacent “stick” states, 1 represents the first pinning state, and 2 represents the second pinning state. According to the experimental results, the polymer ring formed earlier has a larger wavelength, so W₁ is greater than W₂. Thus V₁ is likely to be larger than V₂ for the volume change of the corresponding pinning states. Assume that the solution concentration remains approximately constant and the deposition during the “slip” motion is negligible. The amount of PMMA in V₁, which deposits in the vicinity of the contact line, is greater than that at the following pinning state (P₂), resulting in a polymer ring with larger dimensions at P₁. Note that for certain wavelengths, the circular rings outside the copper ring have greater amplitudes than the circular rings inside the copper ring and the slope of the linear-fitting of the amplitude versus the wavelength for the external concentric rings is slightly larger than that of the internal concentric rings. This asymmetric feature can be attributed to the curvature effect.

Fig. 2 (a) A typical AFM image of the concentric rings formed inside a copper ring; (b) correlation between the amplitude and the wavelength of the concentric rings formed both inside and outside the copper ring (copper ring diameter: 3750 μm, solution concentration: 0.125 wt%, substrate temperature: 21 °C).

Curvature effect

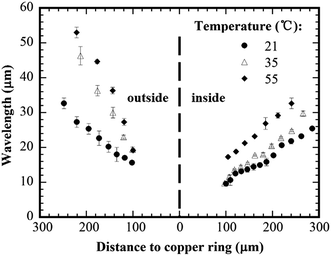
Fig. 3 shows the variation of the wavelength with the distance to copper ring for copper rings of different diameters. The concentration of the PMMA solution was 0.125 wt% PMMA, and the substrate temperature was 21 °C. From Fig. 3, one can note that the wavelength of the concentric rings outside the copper ring decreases approximately linearly with the decrease of the distance to the copper ring for all the three copper rings. For the approximately same distance to the copper ring, the concentric rings formed via a smaller copper ring have larger wavelengths than the concentric rings formed via a larger copper ring, which indicates the curvature effect on the slipping motion of the contact line. For the concentric rings inside the copper ring, the wavelength also decreases with the decrease of the distance to copper ring. There is no significant difference among the concentric rings formed via different copper rings. This result suggests that the curvature effect is more significant for the concentric rings formed outside the copper rings.

Fig. 3 Variation of wavelength with the distance to copper ring for both the concentric rings inside and outside the copper ring for different ring diameters (solution concentration: 0.125 wt% PMMA; substrate temperature: 21 °C).

According to Fig. 3, one notes that the external concentric rings have greater wavelengths than the corresponding internal concentric rings with the approximately same distance to the copper ring. This result suggests that there exists a curvature effect on the slipping motion of the contact lines and the formation of the PMMA rings; the portion of the droplet outside the copper ring (positive curvature) will form concentric rings of larger wavelengths than that inside the copper ring (negative curvature) due to the difference in the confinement to the evaporation of the PMMA–toluene droplets.

Concentration effect

Fig. 4 shows the variation of the wavelength with the distance to copper ring for four solution concentrations. The diameter of the copper ring was 1380 μm. The evaporation took place at a temperature of 21 °C. The wavelengths of both the internal and external concentric rings decrease with the decrease of the distance to the copper ring, independent of the solution concentration, and the external rings have larger wavelengths than the internal rings for the approximately same distance to copper ring. For the approximately same distance to the copper ring, the wavelength increases with increasing the solution concentration for both the internal and external concentric rings.

Fig. 4 Variation of wavelength with the distance to copper ring for four solution concentrations (copper ring diameter: 1380 μm, substrate temperature: 21 °C).

Consider the contact line at a “stick” state. The contact angle gradually decreases due to the evaporation of toluene, and the contact line begins to move to the next “stick” position when the contact angle decreases to a critical value.³⁴ The critical contact angle is determined by the geometrical confinement of the copper ring and the solution concentration. For the same copper ring and the same distance to the copper ring, the geometrical confinement can be approximated as the same. For a solution droplet of a high concentration, the contact line experiences high resistance to the de-pinning and slipping motion due to the interaction with a PMMA ridge of large size and a high viscosity of the solution.

Generally, the viscosity of the PMMA solution increases with the increase of the solution concentration according to the relationship of (η − η₀)/η₀c = [η] + k′[η]²c, where η is the viscosity of the polymer solution, η₀ is the viscosity of the solvent, [η] is the intrinsic viscosity describing the contribution of an individual polymer molecule to the solution viscosity, k′ is the Huggins slope constant for a given “polymer–solvent” system, and c is the concentration of the solution.³⁵ With the evaporation of toluene, there is an increase in local concentration, resulting in the increase of local viscosity and the resistance to the motion of the contact line. More loss of toluene through the evaporation is needed to reduce the contact angle to a smaller critical contact angle³⁴ for initiating the slipping motion of the contact line and a larger tangential force for the slipping motion. The larger tangential force is able to drive the contact line for a liquid film with a larger thickness produced by the polymer solution of a higher concentration to move a greater distance during the slipping than that with a smaller thickness.³⁶

As shown above, the amplitude is a linear function of the wavelength for the experimental conditions used. The dependence of the slope of the amplitude to the wavelength on the solution concentration is depicted in Fig. 5 for the concentric rings formed with three copper ring diameters. The slope of the amplitude to the wavelength increases with the increase of the solution concentration for both the concentric rings inside and outside the copper ring, regardless of the diameters of copper rings. The slope is closely related to the amount of PMMA in droplets. For droplets with the same initial volume, there are more PMMA in a droplet of a higher concentration which are available to form a concentric ridge of larger dimensions near the contact line at a “stick” state for the approximately same slipping distance. Also, a solution of a higher concentration has a higher viscosity, which produces higher viscous resistance to the motion of the contact line and increases the pinning time of the contact line for the deposition of more PMMA.

Fig. 5 Variation of the slope of the amplitude to the wavelength with the solution concentration (substrate temperature: 21 °C).

Fig. 5 also demonstrates the curvature effect. For the same solution concentration, the slope of the amplitude to the wavelength increases with the increase of the diameter of copper rings for the internal concentric rings, while it decreases with the increase of the diameter of copper rings for the external concentric rings.

Temperature effect

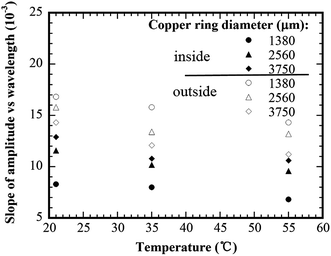
Fig. 6 shows the variation of the wavelength with the distance to the copper ring of a diameter 1380 μm for the concentric rings formed at different substrate temperatures. The solution concentration was 0.125 wt% PMMA. For the same distance to the copper ring, the wavelength increases with increasing the substrate temperature for both the concentric rings inside and outside the copper ring. Such behavior is due to the temperature dependence of the evaporation rate and the solution viscosity. As discussed above, the decrease of the contact angle due to the evaporation introduces the force imbalance on the contact line, leading to the receding of the contact line. During the “slipping” process, the contact angle gradually increases due to the droplet geometry and reaches another “stick” state when the resultant tangential force becomes zero. The evaporation rate increases with temperature, while the solution viscosity decreases with temperature. At a higher temperature, the faster evaporation reduces the time to reach the critical contact angle for the onset of slip motion and also reduces the increasing rate of the contact angle during slipping motion, resulting in a larger driving force for the receding. Moreover, the smaller viscosity reduces the viscous resistance to the motion of the contact line. Thus, the contact line can travel a longer distance before reaching the next pinning (“stick”) state at higher temperatures.

Fig. 6 Variation of wavelength with the distance to copper ring for the concentric rings formed at different substrate temperatures (solution concentration: 0.125 wt% PMMA; copper ring diameter: 1380 μm).

Fig. 7 shows the variation of the slope of the amplitude to the wavelength with the substrate temperature for the concentric rings formed inside and outside the copper rings of three diameters. For all the three copper rings, the slope of the amplitude to the wavelength of both the internal and external concentric rings decreases with the increase of the substrate temperature. This trend suggests that the evaporation temperature plays an important role in controlling the geometrical dimensions of the concentric rings through the control of the evaporation rate and the solution viscosity. The total evaporation time of a solution droplet of 6 μL reduced significantly from 180 s at 21 °C to 110 s at 55 °C. One expects that the pinning time of the contact line also decreases with the increase of the evaporation temperature. Thus, less amount of PMMA was deposited during the “stick” state at a higher substrate temperature for the droplets of the same geometries, and concentric rings of smaller amplitudes were formed.

Fig. 7 Variation of the slope of the amplitude to the wavelength with the substrate temperature (solution concentration: 0.125 wt% PMMA).

In addition, thermal Marangoni flow^37,38 also contributes to the temperature dependence of the dimensions of the concentric rings. The temperature gradient between the dewetting front of a thin liquid film and the top of the film is more profound at a higher substrate temperature than at a lower temperature. This thermal gradient induces an inner circular flow inside the droplet and causes more solute to move from the contact line back to the droplet, resulting in less deposition of solute.³⁹

There also exists the diffusion of polymer due to the concentration gradient induced by the evaporation and the motion of the contact line. The high concentration of polymer around the contact line can cause the diffusion of polymer towards to the center of the droplet, at which the concentration of polymer is relatively low. The diffusion likely reduces the amount of polymer accumulated around the contact line at the “stick” state.

It is known that polymer chains are present in the form of polymer coils with overlapping in dilute solutions, which can be approximated as spheres. The threshold of the overlapping can be determined from the polymer fraction as Φ* = N^−4/5, where N is the degree of polymerization.⁴⁰ For the PMMA used in this study, the degree of polymerization is about 350, and the overlapping threshold is about 0.009. The solution concentrations used in this study in terms of the polymer fraction is in the order of 10⁻⁴, about two orders less than the overlapping threshold 0.009. One can treat the solutions used in this study as dilute solutions, in which the polymer coils are separated particles. Assuming that the flow of the polymer solutions occurs at low Reynolds numbers, the Stokes–Einstein relationship, Dη₀ = k_BT/6πr, can be applied to describe the relationship between diffusion coefficient, viscosity and temperature, where D is the diffusion coefficient, k_B is Boltzmann's constant, r is the radius of the spherical particle and T is absolute temperature.⁴¹ The viscosity of toluene decreases with the increase of temperature from 0.554 mPa s at 298 K, 0.458 mPa s at 315 K to 0.375 mPa s at 335 K.⁴² If the size change of the “polymer sphere” is negligible, the diffusion coefficient increases with increasing the temperature, which suggests that the polymer migrates with a higher rate at a higher temperature than that at a lower temperature. The higher migration rate at higher temperatures also partially contributes to the decrease of the amplitude of the polymer ridges with the increase of the substrate temperature.

Structures in the trenches between two adjacent rings

From Fig. 2a, one notes that the trenches between two polymer ridges are not featureless. There exist small islands in the trenches. Fig. 8 shows typical AFM images of the microscale structures at three different trenches formed at three different substrate temperatures. The diameter of the copper ring was 1380 μm. Fig. 8a–c show the typical structures in the trenches formed at a substrate temperature of 21 °C. At a wavelength of 15 μm, both isolated and interconnected islands can be observed (Fig. 8a). With the increase of the wavelength to 20 μm, the size of the islands increases (Fig. 8b), and the islands become interconnected and a network is formed at a wavelength of 25 μm (Fig. 8c).

Fig. 8 AFM images (5 × 5 μm²) of the patterns formed in the trenches between two adjacent rings at different substrate temperatures (solution concentration: 0.125 wt% PMMA, copper ring diameter: 1380 μm): (a–c) 21 °C, (d–f) 35 °C, (g–i) 55 °C; (j–l) patterns in the trenches between two adjacent rings via the evaporation of a pure toluene droplet on a pre-cast PMMA film (film thickness: ∼90 nm, copper ring diameter: 1380 μm, substrate temperature: 21 °C). The scale bars in all the images represent 1 μm.

At a substrate temperature of 35 °C, large interconnected islands can be found. The size of the islands increases with the wavelength and a continuous film is formed with some larger holes (Fig. 8f). At a substrate temperature of 55 °C, a continuous film with non-uniform holes can be found even for a wavelength of 15 μm (Fig. 8g). The number of the holes significantly decreases for a wavelength of 20 μm (Fig. 8h). A uniform film without any holes can be found in the trench for a wavelength of 25 μm (Fig. 8i). It is worth mentioning that there is no significant difference between the microscale structures in the trenches inside and outside the copper ring.

For comparison, the microscale structures formed in the trenches between two adjacent ridges via the evaporation of a pure toluene droplet on a pre-cast PMMA film are shown in Fig. 8j–l. The film thickness was ∼90 nm, the diameter of the copper ring was 1380 μm, and the substrate temperature was 21 °C. In contrast to the microscale structures formed via the evaporation of the PMMA–toluene droplet, multiple individual holes of micron sizes were formed in the trenches. The hole size does not change with the wavelength significantly. Such behavior is similar to the etching pits formed on the surface of crystalline metals during chemical etching, which reveals the presence of local defects (weak points). The local defects allow the penetration of more toluene locally into the PMMA film, results in the formation of holes after complete evaporation. Note that there are a few larger holes in the trenches for small wavelength of 15 μm (Fig. 8j).

The area fraction of the islands or the continuous film as a function of the wavelength for three substrate temperatures is shown in Fig. 9. The area fraction increases with the increase of the wavelength, suggesting that there are fewer holes over larger trenches for all the three temperatures. For the same wavelength, the area fraction also increases with the increase of the substrate temperature due to easier flow of the solution at a higher temperature.

Fig. 9 Variation of the area fraction of the island patterns in the trenches between two polymer ridges with the wavelength of the concentric rings at three substrate temperatures (solution concentration: 0.125 wt% PMMA, copper ring diameter: 1380 μm).

Note that the height of the islands (or the depth of holes in the continuous film) does not exhibit significant change with the wavelength. They are 27.6 ± 1.9, 34.2 ± 2.4, and 45.4 ± 2.7 nm for the substrate temperatures of 21, 35, and 55 °C, respectively; the height of the islands (or the depth of holes) increases with the increase of the substrate temperature.

The formation of the microscale structures in the trenches is likely due to the deposition of PMMA and the accumulation of “large” amount of toluene during the “slipping” stage. The variation of the dimensions of the microscale structures might be explained from the aspect of the competition between the polymer motion and the motion of the contact line. At room temperature, the evaporation rate is relatively low, the rate of the polymer motion inside a droplet is compatible with the evaporation rate and only a small portion of the polymer directly deposits on the substrate during the “slipping” stage. At a higher temperature, the evaporation rate is significantly high; the contact line recedes to the copper ring at a much faster speed. The liquid film near the contact line might be very thin, leading to a high local viscosity. Thus the polymer may experience a larger resistance and is difficult to keep pace with the motion of the contact line, which results in non-uniform deposition of polymer during the “slipping” stage. Similar situation occurs for the microscale structures formed between the rings of different wavelengths at the same substrate temperature. The evaporation rate is higher and the wavelength is larger when the droplet size is larger. Thus the microscale structures covering a larger area are formed in the wider trenches. It needs to point out that we cannot measure the velocity of the contact line in the small scale and the moving rate of PMMA chains in the thin liquid film near the contact line due to the high receding rate of the contact line during the “slipping” process.

It is worth mentioning that the evaporation behavior at the same wavelength is different for different substrate temperatures due to the differences in the distance to the copper ring, viscosity and evaporation rate. Comparing the micro-structures formed with the same distance to copper ring, one can note the difference. For example, for the distance to the copper ring being 160 μm, from Fig. 6, one can find the wavelength inside the copper ring is about 15 μm at 21 °C, 19 μm (approximately being 20 μm) at 35 °C and 25 μm at 55 °C, respectively. Comparing the microscale structures as shown in Fig. 8 for the corresponding conditions, one can observe significant differences for different substrate temperatures. Moreover, according to Fig. 9, there is an increasing tendency of the area fraction of the microscale structures with the substrate temperature for the same distance to the copper ring.

There are several possible methods which likely can be used to reduce the formation of microscale structures. From the experimental results, it looks like that more PMMA spread uniformly over the area in the trench for a solution of a higher local viscosity during slipping. One can increase local viscosity by increasing the evaporation rate via the increase of the substrate temperature or the solution concentration. Also, one can construct the surface structures via the evaporation of toluene droplets over pre-cast PMMA films. In addition, the interaction among polymer, solvent and the substrate surface plays an important role in controlling the formation of the microscale structures. For polymers not wetting the substrate surface, polymers tend to dewet during the evaporation of solvent and less microscale structures will be formed between adjacent structures. One can limit the motion of the contact line by controlling the change of the contact angle, allowing polymer to keep pace with the motion of the contact line and mitigating the deposition of polymer during the slipping stage.

It is well known that surface contamination and defects, such as dusts and holes, can alter the motion of the contact line and locally pin polymers. This can results in the formation of local structures in the trenches. One needs to reduce the surface contamination and defects through the cleaning of the substrate surface. Note that all of these might introduce local surface structures with different geometrical characteristics (wavelength and amplitude) and topology.

Patterns formed without any templates

Fig. 10 shows the surface structures formed on clean glass slides via the evaporation of droplets of various PMMA solutions without using any templates. The substrate temperature was 21 °C. Only one nearly circular polymer ridge was formed for the solutions of 0.5, 0.25 and 0.125 wt%. Multiple irregular-ring-like structures were formed for the PMMA solution of 0.063 wt% (Fig. 10d and e). The width of the outermost polymer ring increases with increasing the concentration of the solution. Without using the template, there was only one typical “pinning” process during the evaporation of the droplets for the solutions of relatively high concentrations (0.125 wt% or higher) due to high viscosity, and most polymer deposited during the pinning which further increased the pinning force. For dilute solutions, the contact line was able to overcome the resistance at the first pinning state in a relatively shorter time and only a portion of the polymer was deposited, and more deposition occurred at the following several pinning states. It is evident that only irregular surface structures can be formed without using a template to control the evaporation of the droplet of polymer solution.

Fig. 10 Optical images of the surface structures formed via the evaporation of a droplet of PMMA solution on a glass slide without any templates for a solution concentration of: (a) 0.1 wt%, (b) 0.25 wt%, (c) 0.125 wt% and (d and e) 0.063 wt% (substrate temperature: 21 °C).

Fig. 11 shows the patterns formed via the evaporation of droplets of a PMMA solution of ∼0.125 wt% on glass slides without any templates at different substrate temperatures. Only one polymer ring was formed at 21 °C. The number of the polymer rings increases with increasing the substrate temperature from 35 °C to 55 °C. The multiple ring-like patterns formed at higher substrate temperatures is due to the “stick–slip” motions of the contact line controlled by higher evaporation rate and lower viscosity. Comparing the irregular surface structures formed without any templates with those formed with the use of a copper ring, one can conclude that templates play an important role in the fabrication of regular surface structures.

Fig. 11 Optical images of the surface structures formed via the evaporation of droplets of a PMMA solution on glass slides without any templates at different substrate temperatures: (a) 21 °C, (b) 35 °C and (C) 55 °C (solution concentration: 0.125 wt%).

Experimental details

Materials

Poly(methyl-meth-acrylate) (PMMA) (M_w = 35 000) (Fisher Scientific, Pittsburgh, PA) was dissolved in toluene to prepare polymer solutions of different concentrations (0.5, 0.25, 0.125 and 0.063 wt%). The substrate was glass slide (15 × 20 × 1 mm³), which was ultrasonically cleaned in an acetone bath for 5 min for 3 times and dried with condensed air. Copper rings of different diameters (3750, 2560 and 1380 μm) were made from bare copper wires (38 AWG, 79 μm in cross-sectional diameter) (ARCOR, Northbrook, IL). The copper rings were cleaned with toluene ultrasonically and dried at room temperature.

Sample preparation

A copper ring was carefully placed on the surface of a cleaned glass slide. A solution droplet of 6 μL in volume was then dripped on the glass slide, using a micropipette, with the copper ring approximately at the center. The evaporation of the droplets took place at different substrate temperatures (21, 35 and 55 °C), which was controlled by placing the substrates on a heating stage. For the evaporation at 21 °C, the substrates were not heated. For the experiments at 35 and 55 °C, the substrates were pre-heated at the pre-set temperature for half hour to reach thermal equilibrium state before the droplet was dripped on the substrate. Note that the solution was also pre-heated to the pre-set temperature before being dripped on the substrate. During the evaporation, the temperature of the system remained unchanged.

Characterization

The surface patterns formed after complete evaporation of the droplets were characterized, using an optical microscope (Nikon ECLIPSE LV100POL) and an atomic force microscope (Q-scope 250, Agoura Hills, CA). The characteristics of the surface patterns were analyzed, using the AFM software and Image Pro plus.

Conclusion

In summary, we fabricated concentric ring patterns via the evaporation of a droplet of the PMMA–toluene solution by using a copper ring to control the evaporative behavior and the motion of the contact line. Concentric rings were formed both inside and outside the copper ring with a featureless zone in the center. Both the wavelength and amplitude of the concentric rings inside and outside the copper ring decrease with decreasing the distance to the copper ring. There exists the curvature effect, which made the surface structure asymmetric with respect to the copper ring. Both the wavelength and the ratio of the amplitude to the wavelength increase with increasing the solution concentration.

The substrate temperature plays an important role in controlling the formation of the concentric rings. Higher substrate temperature led to the formation of concentric rings of larger wavelengths and smaller ratio of the amplitude to the wavelength for the inner concentric rings. Microscale structures were formed in the trenches between adjacent polymer ridges, whose geometric characteristics were dependent on the wavelength of the concentric rings and the substrate temperature. The technique presented in this study has the potential to fabricate well-ordered concentric ring patterns, whose characteristics can be simply controlled in an effective and economic method. In addition to the parameter studied in this work, other parameters can also be used to control the geometric characteristics of the surface structures formed by using the developed methodology. For example, one can vary the diameter of copper wire, solvent, molecular weight of polymer and surface properties of substrate. Further investigation on the effects of these parameters will make the surface structures more controllable.

References

1. D. Y. Khang, H. Q. Jiang, Y. Huang and J. A. Rogers, Science, 2006, 311, 208–212.
2. B. Kolaric, H. Vandeparre, S. Desprez, R. A. L. Vallee and P. Damman, Appl. Phys. Lett., 2010, 96, 043119.
3. E. P. Chan, E. J. Smith, R. C. Hayward and A. J. Crosby, Adv. Mater., 2008, 20, 711–716.
4. J. Y. Lim and H. J. Donahue, Tissue Eng., 2007, 13, 1879–1891.
5. Y. Fukuhira, E. Kitazono, T. Hayashi, H. Kaneko, M. Tanaka, M. Shimomura and Y. Sumi, Biomaterials, 2006, 27, 1797–1802.
6. R. Langer and D. A. Tirrell, Nature, 2004, 428, 487–492.
7. D. Falconnet, D. Pasqui, S. Park, R. Eckert, H. Schift, J. Gobrecht, R. Barbucci and M. Textor, Nano Lett., 2004, 4, 1909–1914.
8. C. M. Dekeyser, S. Biltresse, J. Marchand-Brynaert, P. G. Rouxhet and C. C. Dupont-Gillain, Polymer, 2004, 45, 2211–2219.
9. L. F. Pease, P. Deshpande, Y. Wang, W. B. Russel and S. Y. Chou, Nat. Nanotechnol., 2007, 2, 545–548.
10. P.-Y. Liang, F. Q. Yang and S. Lee, Mater. Chem. Phys., 2012, 135, 168–173.
11. X. H. Zhang, J. F. Douglas and R. L. Jones, Soft Matter, 2012, 8, 4980–4987.
12. P.-C. Lin, S. Vajpayee, A. Jagota, C.-Y. Hui and S. Yang, Soft Matter, 2008, 4, 1830–1835.
13. R. D. Deegan, O. Bakajin, T. F. Dupont, G. Huber, S. R. Nagel and T. A. Witten, Nature, 1997, 389, 827–829.
14. R. D. Deegan, O. Bakajin, T. F. Dupont, G. Huber, S. R. Nagel and T. A. Witten, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 756–765.
15. Z. Q. Lin and S. Granick, J. Am. Chem. Soc., 2005, 127, 2816–2817.
16. S. W. Hong, S. Giri, V. S. Y. Lin and Z. Lin, Chem. Mater., 2006, 18, 5164–5166.
17. W. Han, M. He, M. Byun, B. Li and Z. Lin, Angew. Chem., Int. Ed., 2013, 52, 2564–2568.
18. W. Han, M. Byun, B. Li, X. Pang and Z. Lin, Angew. Chem., 2012, 124, 12756–12760.
19. H. Yabu, M. Takebayashi, M. Tanaka and M. Shimomura, Langmuir, 2005, 21, 3235–3237.
20. W. Park, T. Tung, H. Shin, J. Han, D. Yoon and W. Yang, J. Mater. Chem., 2012, 22, 22844–22847.
21. Y.-F. Li, Y.-J. Sheng and H.-K. Tsao, Langmuir, 2014, 30, 7716–7723.
22. M. Byun, S. W. Hong, F. Qiu, Q. Zou and Z. Lin, Macromolecules, 2008, 41, 9312–9317.
23. S. W. Hong, J. Xia and Z. Lin, Adv. Mater., 2007, 19, 1413–1417.
24. R. Bao, C. Zhang, Z. Wang, X. Zhang, X. Ou, C. S. Lee, J. Jie and X. Zhang, Chem.–Eur. J., 2012, 18, 975–980.
25. B. Li, W. Han, M. Byun, L. Zhu, Q. Zou and Z. Lin, ACS Nano, 2013, 7, 4326–4333.
26. H. Yabu and M. Shimomura, Adv. Funct. Mater., 2005, 15, 575–581.
27. R. D. Deegan, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 475–485.
28. M. Gonuguntla and A. Sharma, Langmuir, 2004, 20, 3456–3463.
29. U. Olgun and V. Sevínç, Powder Technol., 2008, 183, 207–212.
30. W. Sun and F. Q. Yang, J. Phys. Chem. C, 2014, 118, 10177–10182.
31. H. Bodiguel, F. Doumenc and B. Guerrier, Langmuir, 2010, 26, 10758–10763.
32. H. Uchiyama, D. Shimaoka and H. Kozuka, Soft Matter, 2012, 8, 11318–11322.
33. M. Byun, S. W. Hong, L. Zhu and Z. Lin, Langmuir, 2008, 24, 3525–3531.
34. J. Xu, J. Xia, S. W. Hong, Z. Lin, F. Qiu and Y. Yang, Phys. Rev. Lett., 2006, 96, 066104.
35. M. L. Huggins, J. Am. Chem. Soc., 1942, 64, 2716–2718.
36. W. Sun and F. Q. Yang, Soft Matter, 2014, 10, 4451–4457.
37. Y. Yoshitake, S. Yasumatsu, M. Kaneda, K. Nakaso and J. Fukai, Langmuir, 2010, 26, 3923–3928.
38. H. Hu and R. G. Larson, Langmuir, 2005, 21, 3972–3980.
39. M. Majumder, C. S. Rendall, J. A. Eukel, J. Y. L. Wang, N. Behabtu, C. L. Pint, T. Y. Liu, A. W. Orbaek, F. Mirri, J. Nam, A. R. Barron, R. H. Hauge, H. K. Schmid and M. Pasquali, J. Phys. Chem. B, 2012, 116, 6536–6542.
40. P.-G. De Gennes, Scaling concepts in polymer physics, Cornell university press, 1979.
41. J. T. Edward, J. Chem. Educ., 1970, 47, 261–270.
42. F. J. Santos, C. A. N. de Castro, J. H. Dymond, N. K. Dalaouti, M. J. Assael and A. Nagashima, J. Phys. Chem. Ref. Data, 2006, 35, 1–8.

---