Open Access Article
Open Access ArticleRaman spectroscopic studies and DFT calculations on NaCH3CO2 and NaCD3CO2 solutions in water and heavy water†
Wolfram W.
Rudolph
*a and
Gert
Irmer
b
aTU Dresden, Medizinische Fakultät Carl Gustav Carus, Institut für Virologie im MTZ, Fiedlerstr. 42, 01307 Dresden, Germany. E-mail: Wolfram.Rudolph@tu-dresden.de
bTechnische Universität Bergakademie Freiberg, Institut für Theoretische Physik, Leipziger Str. 23, 09596 Freiberg, Germany
First published on 16th February 2015
Abstract
Sodium acetate and sodium acetate-d3 solutions in water and heavy water were studied using Raman spectroscopy over a wide concentration range and from low wavenumbers (40 cm−1) up to 4200 cm−1. In the terahertz region the broad breathing mode Na–O at 189 cm−1 was detected as well as a broad shoulder at 245 cm−1 of the restricted translation band of acetate–water. Fundamental modes of CH3CO2−(aq) and acetate-d3, CD3CO2−(aq), were assigned and discussed according to pseudo Cs symmetry. The vibrational isotope effect of the CH3/CD3 group was observed and the Teller-Redlich product rule confirmed the assignments. Additionally, band assignments of CH3CO2− and CD3CO2− in heavy water were reported and discussed. By changing from H2O to D2O, relatively strong H-bonding between the oxygen atoms of acetate causes a change in the vibrational energy levels of the dissolved acetate. The symmetric stretching mode of the CO2 group for CH3CO2− in water and heavy water was obtained at 1413.5 cm−1 and 1418.6 cm−1 respectively and for CD3CO2− in water and heavy water, the symmetric stretch was obtained at 1407.5 cm−1 and 1412.4 cm−1, respectively. Coupling of the intramolecular acetate bands is fairly extensive and therefore DFT calculations were carried out on discrete acetate–water (heavy water) clusters. The clusters with the general stoichiometry CH3CO2−·nH2O·mH2O (n = 1–5, m = 1) and n the number of first shell water molecules and m the second shell were considered and calculations at the B3LYP 6-311++G(3df,2pd) level were performed. The frequency calculations on CH3CO2−·5H2O and CD3CO2−·5H2O clusters supported the assignments of the fundamental modes. The geometrical parameters such as bond length and bond angles of acetate in solution state were obtained. The influence of acetate on the O–H stretching band of water was measured as a function of concentration in order to determine the influence of the methyl group on the structure of water. No enhancement of the water structure around the nonpolar methyl group could be detected nor the existence of dangling νO–H bonds at ∼3670 cm−1. In NaCF3CO2 solutions, however, dangling νO–H bonds could be observed at ∼3670 cm−1 caused by the hydrophobic CF3 group. Finally, the nature of the ion pairs formed between Na+ and acetate were discussed in NaCH3CO2(aq) and in concentrated solutions no contact ion pairs could be detected.
1. Introduction
Interest in the study of aqueous carboxylates and carboxylic acids originates from their importance as constituents in biomolecules such as amino acids, fatty acids and surfactants.1,2 Nuclear magnetic resonance (NMR) experiments revealed a hydration number of 5–6 water molecules for the carboxylate group R–CO2− (ref. 3) while X-ray diffraction studies on divalent transition metal acetates gave a hydration number for acetate in the range between 3.0–6.1.4 An X-ray study on NaCH3CO2(aq)5 and a neutron diffraction (ND) investigation6 on NaCH3CO2 in D2O reported a hydration number of 4. Ab initio molecular orbital calculations indicated relatively strong H-bonds between CH3CO2− oxygen atoms and first shell water molecules.7,8 Molecular dynamics (MD) simulations demonstrated, furthermore, that the first-shell waters are either loosely or tightly bound to their CH3CO2− oxygen atoms leading to a fluctuation in the hydration number ranging from 2–5.9 Dielectric relaxation spectroscopic (DRS) measurements on NaCH3CO2(aq) aimed at the hydration, dissociation and ion-pair formation were recently reported.10,11 A combined Raman and infrared spectroscopic investigation on NaCH3CO2(aq) was undertaken and for NaCH3CO2 solutions, it was established that even up to very high concentrations, the acetate forms solvent separated ion pairs with Na+ instead of contact ion pairs and in addition vibrational band assignments of CH3CO2−(aq) were supported by comparison with DFT frequencies.12In this study, we have expanded our work on acetate in aqueous solution to investigate acetate-d3, CD3CO2−(aq), by including the vibrational deuterium isotope effect of the C–H bands (Teller-Redlich product rule) as one central point of interest. It became clear, however, that the acetate bands of the hydrated ion were also affected by changing the solvent from water to heavy water even though the CH3CO2− ion possesses no exchangeable hydrogen at room temperature in its molecular structure. (The same holds true for CD3CO2− which does not possess exchangeable deuterium.) This deuterium solvent effect observed for the acetate and acetate-d3 is the second point of interest in this investigation. Furthermore, the influence of the acetate on the broad O–H stretching band of water and the formation of ion-pairs in NaCD3CO2(aq) and NaCH3CO2(aq) will be dealt with as well. Raman and infrared spectra of NaCH3CO2 and NaCD3CO2 were measured in solution of water and heavy water over a very broad concentration range. Raman spectra were measured to low frequencies at ∼40 cm−1, the terahertz spectral region, which is of current interest studying electrolyte solutions.13
Theoretical frequency calculations assisted in assigning the spectrum of the hydrated acetate and acetate-d3 ions, CH3CO2−(aq) and CD3CO2−(aq) respectively. Geometrical parameters such as bond length and bond angles were obtained by applying DFT calculations. These parameters have been reported first in the gas phase and then with a polarizable continuum (PC) solvation sphere applying a PC model (PCM) in order to simulate the hydration effect.12 Theoretical simulations on selected discrete hydration complexes of acetate with water have been carried out. The chosen cluster approach takes into account the directional nature of the H-bonds formed in aqueous solution. DFT frequency calculations on clusters of light acetate, CH3CO2−·5H2O and CH3CO2−·5D2O, as well as on fully deuterated acetate, CD3CO2−·5H2O and CD3CO2−·5D2O were undertaken. This simple cluster stoichiometry with 5 waters/heavy waters supported the assignments of the intramolecular modes. The different nature of H-bonds formed between acetate and water compared to the ones formed in heavy water (D-bond strength) cannot be addressed by the PC model.
2. Experimental section
2.1. Preparation of the solutions
A NaCH3CO2 stock solution was prepared from dried anhydrous NaCH3CO2 (99.5% extra pure; Merck, Darmstadt, Germany) with triply distilled water free of CO2 by weight. The stock solution was 5.022 mol L−1 (6.506 mol kg−1, Rw = 8.51). Further NaCH3CO2 solutions were prepared: 3.262 mol L−1 (3.822 mol kg−1, Rw = 14.52), 2.184 mol L−1 (2.425 mol kg−1, Rw = 22.94), 1.209 (1.280 mol kg−1, Rw = 43.53), 0.810 (0.842 mol kg−1, Rw = 66.17), 0.161 (0.162 mol kg−1, Rw = 341.80), and 0.0325 mol L−1 (0.0328 mol kg−1, Rw = 1702.71). The solutions of sodium acetate react alkaline a dn the pH value of a 0.161 mol L−1 solution at 23 °C = 8.8. The acetate solutions were sealed in plastic, air tight bottles in order to prevent the uptake of CO2 from air. The solution densities were determined with a pycnometer of 5.000 mL volume at 23 ± 0.1 °C. From the solution densities and the concentrations in mol L−1, the concentrations in mol kg−1 were calculated and from the latter, the Rw – values were determined. Rw – values represent the number of moles of water per one mole of salt.Three NaCH3CO2 solutions in heavy water (99.9% D; Merck, Darmstadt, Germany) were prepared from dried anhydrous NaCH3CO2 and heavy water by weight. The following solutions were prepared: 3.944, 0.790 and 0.262 mol L−1.
Sodium acetate-d3, NaCD3CO2, (Aldrich; 99% D) solutions in water were prepared with a concentration at 2.936 mol L−1 (3.377 mol kg−1, Rw = 16.44) 1.468 mol L−1 (1.572 mol kg−1, Rw = 35.29) and 0.294 mol L−1 (0.298 mol kg−1, Rw = 185.92).
A sodium acetate-d3, NaCD3CO2 (Aldrich; 99% D) solution in heavy water was prepared with a concentration of 2.792 mol L−1 and 0.972 mol L−1.
Six aqueous NaCF3CO2 (Sigma-Aldrich; 99%) solutions were prepared from dried anhydrous NaCF3CO2 and water by weight. The following solutions were prepared: 3.554 mol L−1 (Rw = 12.24), 2.865 mol L−1 (Rw = 15.94), 1.424 mol L−1 (Rw = 35.73), 0.850 mol L−1 (Rw = 61.98) and 0.427 mol L−1 (Rw = 126.78). A hydrous NaCF3CO2 melt was also prepared at 9.35 mol L−1 (Rw = 2.48).
2.2. Raman spectra
Raman spectra were measured in the macro chamber of a T 64000 Raman spectrometer from Jobin Yvon in a 90° scattering geometry at (23 ± 0.1) °C. The solutions have been measured in high precision quartz cuvettes from Hellma Analytics (Müllheim, Germany) which were sealed with an air tight stopper. The spectra were excited with the 487.98 nm line of an Ar+ laser at a power level of ∼1100 mW at the sample. After passing the spectrometer in subtractive mode, with gratings of 1800 grooves per mm, the scattered light was detected with a cooled CCD detector.14,15IVV and IVH spectra were obtained with fixed polarisation of the laser beam by rotating the polarizer at 90° between the sample and the entrance slit to give the scattering geometries: IVV = I(Y[ZZ]X) = 45α′2 + 4γ′2 and IVH = I(Y[ZY]X) = 3γ′2. The isotropic spectrum, Iiso, was then constructed:| Iiso = IVV − 4/3IVH | (1) |
The depolarization ratio, ρ, was determined according to:
| ρ = IVH/IVV = 3γ′2/(45α′2 + 4γ′2) | (2) |
The polarization analyser was calibrated with CCl4 before each measuring cycle and adjusted if necessary (for details see ref. 14).
The wavenumber positions have been checked with Neon lines and the peak positions for bands with smaller band width (full width at half height; fwhh) have been determined with an error of ±0.5 cm−1 and broader bands fwhh ≥ 25–30 cm−1 with a precision of ±1 cm−1. In dilute solutions, the signal to noise ratio (S/N) was excellent for the spectra at >450.
Band intensities have been determined by fitting the bands using Gaussian–Lorentzian product functions on baseline corrected spectra. Relative band intensities for CH3CO2−(aq), and CH3CO−(D2O) as well as for CD3CO2−(aq) and CD3CO2−(D2O) were presented so that the strongest mode was set to 100 and the band intensities of the other modes relative to this value. Details of the band fitting procedure of the baseline corrected Raman-bands were described elsewhere.16
Spectra in R-format (Bose–Einstein correction) were obtained. The isotropic spectrum, Riso was then constructed similar to eqn (2): Riso = RVV − 4/3RVH. The isotropic R-spectra have been used to characterize the restricted translation band of water and restricted translation band of water and acetate (O–H⋯O*). A more detailed description of the Raman measurements and the construction of the spectra in R-format is given in ref. 14 and 17.
2.3. Density functional theory calculations
For the purpose of modeling the vibrational frequencies the DFT calculations were performed employing the B3LYP functional with a triple-ζ basis set 6-311++G(3df,2pd) from the Gaussian 03 program suite.18 The geometry of the acetate ion was then optimized and frequency calculations allowed the assignments of the fundamental modes. Proper description of anions with electrons which are located, on average, relatively far from the nuclei, require diffuse orbitals and polarization basis sets. The optimization procedure led to the result that the geometry of the CH3CO2− with the dihedral angle φ = 0° is stable and possesses no imaginary frequency. DFT frequency calculations were performed for this stable configuration in the gas phase and in addition in the presence of the solvent (water) by placing the solute within the solvent.19 The latter was modelled as an isotropic and homogeneous continuum characterized by its dielectric properties. The frequencies were calculated with a floating cavity (a set of interlocking spheres attached to the solute atoms). The electrostatic solute–solution interaction was calculated introducing an apparent charge distribution spread on the cavity surface. The PC model implemented in the GAUSSIAN package was used as described in ref. 19.A second approach, the discrete cluster approach, was applied in order to model the solvent effects of H2O and D2O taking into account the directionality of the hydrogen bonds between acetate and water and heavy water. The different strength of H-bonds formed between acetate and water was compared to the ones formed in heavy water, the deuterium bond strength. Acetate–water clusters, with an increasing number of water molecules from 1 to 6 water molecules were optimized with the cluster stoichiometry CH3CO2−·nH2O·mH2O (n = 1–5, m = 1) with n the number of first shell water molecules and m the second shell water. The H-bonding of the water molecules occurs around the oxygen atoms of the –CO2 group (the CH3 group is effected much weaker through hydrophobic interaction). No symmetry constraints were employed for the cluster calculations. The calculated structures were minima on the potential energy surface (PES) confirmed by frequency calculations to ensure that the structures were local minima. Once a local minimum was found, the structure was perturbed and re-optimized to see if a lower energy local minimum could be found. The second derivative of the energy with respect to the nuclear positions then allows the calculation of the frequencies.
3. Results and discussion
From here on the paper is organized as follows: first, the structures and symmetries of acetate–water clusters are presented with particular focus on the cluster with 5 water molecules. Then, a brief discussion of the terahertz frequency region is given, including the spectral influence of the Na+(aq) and the restricted translation modes of acetate and water. This is then followed by an examination and assignment of the Raman spectroscopic intramolecular acetate bands in aqueous solutions on CH3CO2− and CD3CO2− using the DFT frequencies of the discrete cluster with 5 water molecules to guide in the assignments. Next, the aqueous solvent isotope effects in light and heavy water for CH3CO2− and CD3CO2− are presented and discussed. A description of the influence of the acetate on the O–H band of water is given including the hydrophobic effect of the methyl group. Finally, the different ion-pairs of acetate with Na+ formed in these solutions are briefly presented.3.1. Symmetry of the CH3CO2− ion and acetate–water clusters
The conformer of the CH3CO2− gas phase ion with the dihedral angle φ = 0° is by 11 cal mol−1 more stable than the conformer, φ = 29° (ref. 12) (both structures possess Cs symmetry). The structure of the gas phase ion (bond lengths and angles) for φ = 0° resulted in a non-equivalence of the two oxygen atoms of the –CO2 group (Fig. 3, ref. 12). Because of the slight energy difference between the two conformers in comparison with the thermal energy quantum kT (576 cal mol−1 at 290 K), the calculated frequencies of the two conformers differ nominally from each other and are within the band width of the observed acetate bands.Applying the PC method to account for the hydration effect in aqueous solution resulted in good frequency values for CH3CO2−(aq)12 but it is unable to account for the directionality of the H-bonds between acetate and H2O. Modeling the influence of solvation (i.e. hydration) by applying a structureless PC around the species will not result in calculable frequency changes by going from water to heavy water as a solvent. Water at 25 °C has a ε-value of 78.54 while D2O possesses ε = 78.06. Such a small difference in ε cannot explain the change of the acetate frequencies using PCM.
The acetate–water cluster with 5 waters (CH3CO2−·5H2O) which will be discussed in greater detail resembles a realistic model for the hydrated acetate ion. The directional nature of the H-bonds for the cluster structure for CH3CO2−·5H2O is shown in Fig. 1 and the geometrical parameters in Table 1. The CH3CO2− in this cluster possesses a dihedral angle of 14.7° which leads to symmetry C1. Including the CH3CO2−·5H2O cluster, six cluster models of acetate with increasing number of water molecules (see Experimental section) were optimized and for completeness all results are presented in Table S1† and the structures in Fig. S1.†
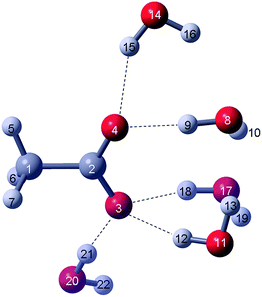 | ||
| Fig. 1 DFT model of the CH3CO2−·5H2O cluster. The numbering of the acetate ions (atoms 1–7: C-atoms: 1, 2; O-atoms: 3, 4 and H-atoms 5–7) is the same as for the gas phase cluster given in ref. 12; the oxygen atoms of the five water atoms are labelled 8, 11, 14, 17 and 20. The H-atoms of these water molecules (atoms 9–22) are labelled accordingly. | ||
| Parameter | CH3CO2−in vacuo | CH3CO2− + solvation sphere | CH3CO2−·5H2O |
|---|---|---|---|
| a n.a. = not applicable. | |||
| a 1,2 | 1.561 | 1.533 | 1.526 |
| a 2,3 | 1.253 | 1.261 | 1.269 |
| a 2,4 | 1.2525 | 1.259 | 1.250 |
| a 1,5 | 1.091 | 1.088 | 1.087 |
| a 1,6 | 1.093 | 1.091 | 1.089 |
| a 1,7 | 1.093 | 1.091 | 1.092 |
| α 3,2,4 | 128.84° | 125.40° | 125.03° |
| α 5,1,6 | 109.51° | 109.30° | 110.55° |
| α 5,1,7 | 109.51° | 109.30° | 108.88° |
| α 6,1,7 | 107.03° | 107.04° | 107.18° |
| d 4,2,1,5 | 0° | 0° | 14.71° |
| a 3,12 | n.a. | n.a. | 2.032 |
| a 3,18 | n.a. | n.a. | 1.947 |
| a 3,21 | n.a. | n.a. | 1.780 |
| a 4,9 | n.a. | n.a. | 1.756 |
| a 4,15 | n.a. | n.a. | 2.016 |
| a 3,11 | 2.967 | ||
| a 3,17 | 2.886 | ||
| a 3,20 | 2.762 | ||
| a 4,8 | 2.741 | ||
| a 4,14 | 2.907 | ||
From the results of the discrete cluster calculations, it is clear that with an increasing number of water molecules hydrating the oxygen atoms of the –CO2 moiety, the following takes place: shortening of the C–C bond distances, change of the dihedral angle ≠ 0° (loss of Cs symmetry) and the change of the C–O bond lengths of the two C–O bonds leading to a slightly longer bond and one slightly shorter. The acetate water cluster with one water molecule, CH3CO2−·H2O still possesses Cs symmetry and the water molecule binds in a bifurcated fashion to the two oxygen atoms of the –CO2 moiety. The DFT calculations led to a symmetrical geometry and an energy minimum on the PES was obtained (Fig. S1†). However, this is not a realistic model for structural and energetic reasons.20 Bifurcated bound water molecules with acetate would lead to an artificially narrow restricted translation band at ca. 216 cm−1 (DFT result) which is clearly in conflict with the observed broad restricted translation mode of water bound to acetate.12 For the cluster with n = 2, CH3CO2−·2H2O, the water molecules hydrating the acetate ion form two relatively strong H-bonds with each water molecule yielding slightly different H-bond lengths (Fig. S1 and Table S1†). Due to asymmetric binding of the water molecules, clusters with n > 2 cause the CH3CO2− ion to be distorted (φ ≠ 0°) and its symmetry is, strictly speaking, C1 (Cs with small deviations). The cluster with four water molecules reflects a realistic snapshot of the hydration process which was demonstrated by MD calculations.9 The cluster with six H2O molecules represents an example of a cluster with 5 waters in the first sphere and the sixth water in the second sphere. From a variety of structural investigations3–6 and theoretical calculations,7–9 however, it became evident that the –CO2 group is hydrated by ∼5 water molecules. The geometry optimized CH3CO2−·5H2O cluster was used to calculate the second derivative of the energy, with respect to the nuclear positions, in order to yield frequencies of the acetate ion and the water molecules of the first hydration sphere.
The result of the CH3CO2−·5H2O cluster model describes the hydrated acetate ion in solution quite well (Fig. 1). The numbering of the atoms of the acetate ion is the same as in ref. 12 and thus allows comparison of the parameters with the ones presented in Table 1 (ref. 12). A recent DRS study10 reported two strong H-bonds with two H2O molecules with the acetate and a total hydration number of ∼11 at infinite dilute solution. Five of 11 water molecules weakly and strongly interact with the oxygen atoms of the –CO2 unit while the other six water molecules surround the CH3 group forming a weakly interacting cluster structure (hydrophobic interaction).7,10 The PC method does not take into account the directional forces of the H-bonds formed between water and the –CO2 moiety of acetate and is not helpful in this context. Although the frequencies derived from the PC model are satisfactory and useful for the assignments of the fundamental modes of CH3CO2−, certain modes deviate quite noticeably from the measured frequencies. The discrete cluster model presented offers a remedy for this problem.
The geometrical parameters of the CH3CO2−·5H2O cluster model compared with those of the unhydrated acetate ion (Table 1) reveal that the C–C bond distance shortens, the C–O bond distances differ in bond length quite noticeably, and a dihedral angle at 14.7° results in a loss of the symmetry plane and, subsequently, a loss in symmetry (C1).
3.2. The terahertz frequency region of the Na-acetate solutions
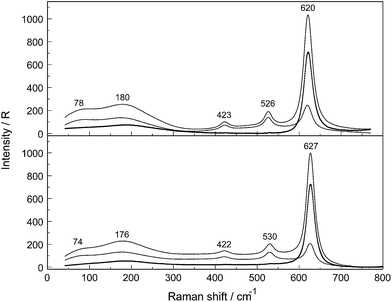
Aqueous solutions of NaCH3CO2 are strongly dissociated in dilute solutions forming Na+(aq) and CH3CO2−(aq) but ion pair formation should be taken into account in concentrated solutions. In NaCH3CO2 solutions, the ion pairs formed are of the outer-sphere and outer–outer-sphere type with water molecules interposed between Na+ and CH3CO2−. The types of ion pairs change significantly with concentration. Completely hydrated Na+ and CH3CO2− are formed in very dilute solutions. In more concentrated solutions, outer–outer-sphere ion-pairs form and in the most concentrated ones ion pairs with one water molecule interposed between Na+ and CH3CO2− are formed. The question arises as to whether direct ion pairs are formed in these solutions and this will be discussed in Section 3.4.A comparison of the Raman spectra in R-format in the terahertz frequency region are given in Fig. 2 for NaCH3CO2 in water and heavy water while the ones for NaCD3CO2 are given in Fig. 3. The Na+ ion in aqueous solution is hydrated and a very broad band at ∼189 cm−1 (isotropic scattering, 185 cm−1 in the polarized scattering; Fig. 2 upper panel) was detected.12,21 A neutron scattering study combined with Raman spectroscopic measurements21 revealed an isotropic band at 185 cm−1 which is quite close to our value. A Na+-tetra- or -penta-hydrate has to be assumed because our high level DFT cluster calculations revealed that the Na+-hexahydrate is not stable while tetra and penta-aqua Na+ clusters are. Both clusters give a quite similar ν1Na–O stretching band at 196 and 192 cm−1 respectively. For the deuterated Na+tetra- and penta-clusters, the peak frequencies were calculated at 186 cm−1 and 178 cm−1 respectively in good accord with the measured peak position at 178 cm−1 in the polarized scattering and at 180 cm−1 in the isotropic scattering for NaCH3CO2(D2O) (Fig. 2, lower panel)‡. The calculated frequencies are quite close together and cannot be used to determine which cluster is prevalent. Most of the values for the first hydration number were given at 5 and an internuclear distance Na–O with 2.34 Å.22,23 Our DFT frequency calculations on [Na(OH2)4]+ and [Na(OH2)5]+ led to stable structures while [Na(OH2)6]+ gave no stable structure. Recent MD modelling confirmed that the Na+-hexa-hydrate is only one of the possible hydrated species along with the tetra- and penta-hydrates.22–25
In addition to the Na–O stretching mode at 189 cm−1 a broad band contribution at 245 cm−1 appeared (Fig. 2, upper panel) and was assigned to the restricted translation band, νsO–H⋯O, reflecting the strong H-bonds between both oxygen atoms of the –CO2− group and H2O.12 This restricted translational mode, determined by acetate water hydrogen bonds, becomes less important with dilution and in dilute acetate solutions this mode appears as a weak polarized band at 175 cm−1 due to O⋯H–O bonds between the water molecules. In NaCH3CO2 solution in heavy water a similar restricted translation band, νsO–D⋯O, reflecting the D-bonds between oxygen atoms of the –CO2− group and D2O appears at 233 cm−1 (see Fig. S2†). A weak polarized band due to O⋯D–O bonds between the heavy molecules appears at 169 cm−1 in neat D2O(l).
The cluster with five water molecules (Fig. 1) reveals bond distances of OOAc--⋯OH2O (O⋯H–O nearest-neighbor distances of the H-bond) from 2.741 Å to 2.967 Å (Table 1). These are in good agreement with the experimental values between 2.77 and 2.95 from X-ray diffraction studies on concentrated divalent transition metal acetates4 and with a value at 2.78 Å from later measurements on an aqueous 8 mol% NaCH3CO2 solution.6 Recent neutron scattering data support the X-ray diffraction values and the radial distribution curves of the two C⋯O and O⋯O distances, calculated with MD simulations, show peaks at 3.4 Å and 2.7 Å, respectively.9 It should be noted that the CH3 group has little effect on the geometry of the hydration shell which reveals that the radial distribution curves for HCO2−⋯HOH is comparable with that for CH3CO2−⋯HOH. The cluster model with five water molecules shows frequencies at 206 and 219 cm−1 which are slightly lower than the peak position of the broad shoulder observed at ∼245 cm−1.
3.3. Fundamental frequencies of CH3CO2− and CD3CO2− – vibrational spectroscopic results on CH3CO2−(aq) and CD3CO2−(aq)
The acetate cluster with five water molecules forming single H-bonds with the two oxygen atoms of the –CO2 group represents a realistic cluster modelling the acetate in water (see Section 3.1.). The second derivative of the energy with respect to the nuclear positions then allowed the calculation of the frequencies for the {CH3CO2−·5H2O} model. Comparison of the DFT frequencies of CH3CO2− in the gas phase with ones in solution show the strong effect of hydration on acetate in solution state especially the pronounced frequency shifts of the –CO2 group, such as both stretching modes, νs and νas of the CO2 group, the deformation mode of the –CO2 moiety, δCO2, and the rocking mode (ρ). This is reinforced by comparing the measured frequencies of the acetate in water and heavy water showing changes in the fundamental modes with respect to peak positions and intensities. In other words, the acetate modes will change despite the fact that the molecule does not contain exchangeable H(D) in its structure. The cluster model with five water molecules which take into account the directionality of the H-bonds enables modelling of the deuterium effect of the solvent followed by change from H2O to D2O. The DFT frequencies for CH3CO2−·5H2O(D2O) and CD3CO2−·5H2O(D2O) clusters are presented in Tables 2 and 3. The vibrational modes are mixed on the PES and therefore assignment of the normal modes is difficult. However, DFT frequencies are an excellent guide in assigning the fundamental modes of acetate in solution of water and heavy water.| CH3CO2−(aq) | CH3CO2−(D2O) | Numbering of modes and symmetry | Assignment | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ν max/cm−1 | fwhh/cm−1 | Integr. intensity | Depol. ratio | B3LYP 6-311++(3df,2pd) cluster | ν max/cm−1 | fwhh/cm−1 | Integr. intensity | Depol. ratio | B3LYP 6-311++(3df,2pd) cluster | ||
| a n.d. not detected. * bands severely overlapped. + average wavenumber from two equally contributing fundamentals due to coupling of the solute modes with the ones of water. | |||||||||||
| n.d. | — | — | — | 65.9+ | n.d. | — | — | — | 64.1+ | ν 15(a′′) | τCO2 |
| 474 | 21 | 0.254 | 0.70 | 483.1 | 474 | 23 | 0.442 | 0.70 | 469.6 | ν 10(a′) | ρCO2 |
| 620.7 | 21.3 | 0.262 | 0.75 | 617.6+ | 626.8 | 16 | 0.439 | 0.75 | 621.2 | ν 14(a′′) | ωCO2 |
| 654.2 | 25.9 | 2.375 | 0.346 | 658.0 | 661.5 | 20 | 4.138 | 0.340 | 662.5+ | ν 9(a′) | δCO2 |
| 928.4 | 11.4 | 9.874 | 0.054 | 926.0+ | 927.2 | 11.4 | 25.80 | 0.054 | 925.2 | ν 8(a′) | νC–C |
| 1021.5 | 26.5 | 0.231 | 0.70 | 1032 | 1022 | 26.5 | 0.691 | 0.74 | 1031.6 | ν 7(a′) | ρCH3 |
| 1052 | 27 | 0.032 | 0.75 | 1064 | 1053 | 27 | 0.054 | 0.7 | 1064.5 | ν 13(a′′) | ωCH3 |
| 1347.6 | 11 | 1.884 | 0.367 | 1367 | 1349.5 | 11 | 4.259 | 0.367 | 1367.5 | ν 6(a′) | δCH3 |
| 1413.5* | 24.6 | 15.07 | 0.26 | 1418.6 | 1417.8* | 22 | 33.50 | 0.26 | 1420.2 | ν 5(a′) | ν sCO2 |
| 1426* | 26 | 0.297 | 0.5 | 1468.3 | 1429* | 28 | 1.926 | 0.5 | 1468.5 | ν 4(a′) | δ sCH2 |
| 1440* | 18 | 0.297 | 0.75 | 1485.8 | 1444* | 17 | 2.003 | 0.75 | 1485.8 | ν 12(a′′) | δ asCH2 |
| 1556 | 44 | 1.238 | 0.62 | 1612.0 | 1563 | 42 | 4.248 | 0.60 | 1615.7 | ν 3(a′) | ν asCO2 |
| 2935.5 | 22.5 | 100.0 | 0.005 | 3032.9 | 2936.0 | 21.5 | 100.0 | 0.008 | 3032.9 | ν 2(a′) | ν sCH3 |
| 2984 | 23.5 | 3.666 | 0.74 | 3094.0 | 2983 | 24 | 4.391 | — | 3094.1 | ν 11(a′′) | ν asCH3 |
| 3014 | 34.6 | 4.832 | 0.7 | 3124.7 | 3016 | 35 | 4.006 | n.d. | 3124.8 | ν 1(a′) | ν asCH3 |
| CD3CO2−(aq) | CD3CO2−(D2O) | Numbering of modes and symmetry | Assignment | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ν max/cm−1 | fwhh/cm−1 | Integr. intensity | Depol. ratio | B3LYP 6-311++(3df,2pd) | ν max/cm−1 | fwhh/cm−1 | Integr. intensity | Depol. ratio | B3LYP 6-311++(3df,2pd) | ||
| a n.d.: not detected. * bands severely overlapped. | |||||||||||
| n.d. | — | — | — | 39.4+ | n.d. | — | — | — | 38.8+ | ν 15(a′′) | τCO2 |
| 422.5 | 28.5 | 1.31 | 0.71 | 412.4 | 421.0 | 28.5 | 1.10 | 0.72 | 425.2 | ν 10(a′) | ρCO2 |
| 526.5 | 19.5 | 1.48 | 0.75 | 531.6+ | 529.5 | 24 | 1.60 | 0.75 | 529.3 | ν 14(a′′) | ρCO2 |
| 621.0 | 23.5 | 12.06 | 0.17 | 619.8+ | 627.0 | 21.5 | 14.02 | 0.17 | 619.0 | ν 9(a′) | δCO2 |
| 834.1 | 15.0 | 1.534 | 0.70 | 839.3 | 834.5 | 10 | 1.483 | 0.71 | 837.8 | ν 8(a′) | ρCD3 |
| 885.2 | 14.1 | 29.43 | 0.037 | 876.6 | 882.8 | 11 | 35.73 | 0.038 | 884.0 | ν 7(a′) | νC–C |
| 937 | 15 | 0.216 | 0.73 | 940.6 | 936 | 15 | 0.245 | 0.73 | 939.0 | ν 13(a′′) | ρCD3 |
| 1035* | 21 | 0.5 | 0.6 | 1059.1 | 1035* | 20 | 0.4 | 0.50 | 1059.0 | ν 6(a′) | δCD2 |
| 1043* | 38 | 4.93 | 0.74 | 1067.8 | 1042* | 40 | 5.87 | 0.754 | 1067.8 | ν 12(a′′) | δCD2 |
| 1086.4 | 11.4 | 19.54 | 0.042 | 1096.8 | 1085.8 | 11.4 | 20.87 | 0.042 | 1096.4 | ν 5(a′) | δCD2 |
| 1407.5 | 17.5 | 57.50 | 0.240 | 1412.4 | 1410.5 | 18.2 | 62.36 | 0.240 | 1414.3 | ν 4(a′) | ν sCO2 |
| 1546.5 | 62 | 12 | 0.52 | 1603.0 | 1551.5 | 46 | 9.585 | 0.52 | 1606.4 | ν 3(a′) | ν asCO2 |
| 2112.5 | 13.4 | 100 | 0.006 | 2178.4 | 2112.5 | 13.4 | 100.0 | 0.006 | 2178.4 | ν 2(a′) | ν sCD3 |
| 2188 | 18.4 | 63.97 | — | 2288.1 | 2188 | 18.4 | 51.23 | 0.74 | 2288.1 | ν 11(a′′) | ν asCD3 |
| 2265 | 62 | 37.20 | — | 2318.0 | 2231 | 20.5 | 4.94 | — | 2318.0 | ν 1(a′) | ν asCD3 |
Because of the small deviation from Cs symmetry, acetate is treated as having pseudo Cs symmetry. The 15 normal modes of the CH3CO2− ion of the gas phase structure with φ = 0° belong to the point group Cs and span the representation: Γvib(Cs) = 10a′(Ra, i.r.) + 5a′′(Ra, i.r.). All modes are Raman and i.r. active and the modes with the character a′ are partially polarized while the ones with symmetry a′′ are depolarized.
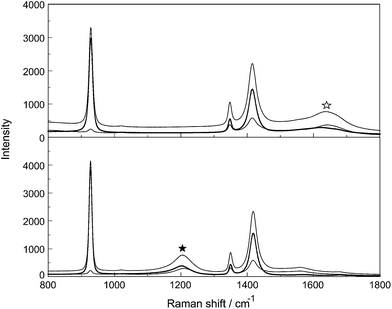
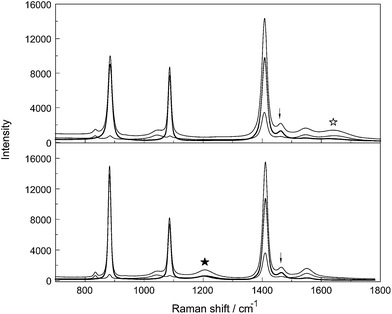
Stretching band parameters are concentration dependent especially for bands of the –CO2 group such as νsCO2 and νasCO2 and therefore extrapolation to concentration zero resulted in the band parameters of infinitely dilute solution. The Raman spectroscopic data for aqueous NaCH3CO2 and NaCD3CO2 are summarized in Tables 2 and 3, respectively, and representative Raman spectra of CH3CO2−(aq) and CD3CO2−(aq) are presented in Fig. 4 and 5 respectively. For assignment purposes, the CH3CO2− spectra in D2O have been measured in order to observe the antisymmetric stretching mode of the –CO2 group undisturbed from the broad deformation band of water at 1641 cm−1 as well as the CH3 stretching modes which are overlapped by the very broad O–H stretching profile of water. CD3CO2− spectra in H2O and in D2O were measured. The Raman data for NaCH3CO2 and NaCD3CO2 solutions in heavy water are also given in Tables 2 and 3, respectively.
Inspection of the spectra in Fig. 4 and 5 and the data in Tables 2 and 3 indicates that there are two distinct vibrational regions for the acetate and acetate-d3. Regions from 400–1700 cm−1 and from 2800–3100 cm−1 for CH3CO2− were identified and from 400–1700 cm−1 and from 1900–2400 cm−1 for CD3CO2−.
The C–H stretching modes are somewhat decoupled from the rest of the vibrational modes and lie above 2900 cm−1 for the C–H bands and 2100 cm−1 for the C–D bands (Fig. 2 and 3, left panels). Three bands at 2935.5 cm−1, the strongest mode in Raman, ν2(a′) and the much weaker bands at 2984 and 3014 cm−1, numbered ν13(a′′) and ν1(a′) respectively, are assigned to the stretching bands of the CH3 group. The ν2(a′), the νsCD3 mode in CD3CO2−(aq) shows a large frequency shift due to the changes in masses from H to D and the corresponding fundamental frequency decreases by the factor  , the square root of the ratio of masses. The νsCD3 mode in CD3CO2−(aq) appears at 2112.5 cm−1 and the ratio νsCD3/νCH3 has an experimental value of 0.719, compared with the theoretically expected value of 0.707. The discrepancy is attributed to the fact that the C–H/C–D vibrations are not strictly harmonic and may be further complicated by Fermi resonance.26 One other fact is remarkable, namely, that the peak position of ν2(a′) C–H at 2935.5 cm−1 hardly changes with increasing concentration. However, the fwhh broadens with increasing NaCH3CO2 concentration by only a few wavenumbers. The fwhh of ν2(a′) C–H for a 5.02 mol L−1 NaCH3CO2 solution is 23.1 cm−1 and decreases in width with concentration and is ∼21 cm−1 for a solution at zero concentration. (It is noteworthy that a severe broadening and a small wavenumber shift occurs in La(CH3CO2)3(aq)27). This fact shows that the C–H bonds are barely influenced by hydration which is believed to be due to the hydrophobic interaction effect. Calculations on CH4(aq) suggests that the methyl group will only contribute ca. 1 kcal mol−1 to ΔHhydr. at 25 °C (ref. 8, page 305).
, the square root of the ratio of masses. The νsCD3 mode in CD3CO2−(aq) appears at 2112.5 cm−1 and the ratio νsCD3/νCH3 has an experimental value of 0.719, compared with the theoretically expected value of 0.707. The discrepancy is attributed to the fact that the C–H/C–D vibrations are not strictly harmonic and may be further complicated by Fermi resonance.26 One other fact is remarkable, namely, that the peak position of ν2(a′) C–H at 2935.5 cm−1 hardly changes with increasing concentration. However, the fwhh broadens with increasing NaCH3CO2 concentration by only a few wavenumbers. The fwhh of ν2(a′) C–H for a 5.02 mol L−1 NaCH3CO2 solution is 23.1 cm−1 and decreases in width with concentration and is ∼21 cm−1 for a solution at zero concentration. (It is noteworthy that a severe broadening and a small wavenumber shift occurs in La(CH3CO2)3(aq)27). This fact shows that the C–H bonds are barely influenced by hydration which is believed to be due to the hydrophobic interaction effect. Calculations on CH4(aq) suggests that the methyl group will only contribute ca. 1 kcal mol−1 to ΔHhydr. at 25 °C (ref. 8, page 305).
The Teller-Redlich product rule28,29 proved to be useful for the assignments of the fundamental modes of the isotopomers. This rule was used to check the assignments of the CH3CO2− ion and its deuterated analog, CD3CO2−. For the two species a′ and a′′ of the point group Cs the following formulae apply:
 | (3a) |
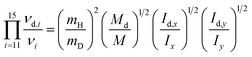 | (3b) |
 | (4) |
The symbol νi(νd,i) denotes the frequencies of the ion (deuterated ion), the index I numerates the 10 and 5 normal vibrations of the a′ and a′′ species, respectively. M(Md) are the total masses of the ions, Ix, Iy, Iz (Idx, Idy, Idz) are the moments of inertia about the x, y, and z axes through the center of mass, mi(md,i) denote the masses of the atoms of the ions. (The x, y axes were chosen lying in the symmetry plane, the z axis perpendicular to it.)
The theoretical results for the product of frequency quotients obtained from DFT calculations are:  ,
,  , and
, and  .
.
Inserting the measured Raman frequencies (see Tables 2 and 3), we obtain:
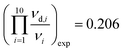 ,
,  , and
, and 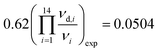 in reasonable agreement with the theoretical values. Because the torsional vibrations ν15(νd,15) with the lowest frequency values could not be measured, the quotient of the theoretical values was used instead, (νd,15/ν15)exp = (νd,15/ν15)th = 0.62.
in reasonable agreement with the theoretical values. Because the torsional vibrations ν15(νd,15) with the lowest frequency values could not be measured, the quotient of the theoretical values was used instead, (νd,15/ν15)exp = (νd,15/ν15)th = 0.62.
The frequencies for the CO2 group increase by changing from H2O to D2O for both acetate species namely CH3CO2− and CD3CO2−. For example, for CH3CO2−(aq) and CH3CO2−(D2O) the deformation mode, δCO2 appears at 654.2 cm−1 for the former and at 661.5 cm−1 for the latter, while νsCO2 occurs at 1413.5 cm−1 and at 1418.2 cm−1, respectively. The same is true for νasCO2 which occurs at 1556 cm−1 in water and at 1563 cm−1 in heavy water (data in Table 2). For acetate-d3, CD3CO2−, in water and heavy water, δCO2 appears at 621 cm−1 for the former and at 627 cm−1 for the latter while νsCO2 occurs at 1407.5 cm−1 and at 1410.5 cm−1, respectively. The antisymmetric stretch, νasCO2, for acetate-d3 in water and heavy water occurs at 1546 cm−1 and 1552 cm−1, respectively (Table 3). The acetate cluster model with 5 water molecules reflects the H2O–D2O solvent isotope effect quite well. These DFT frequencies for CH3CO2− and CD3CO2− in water and heavy water are presented in Tables 2 and 3, respectively. This change of water to heavy water simply means that the deformation mode and the symmetric stretch of the CO2 group get stiffer in heavy water. This may be due to a simple mass effect but the different hydrogen bond strength versus the deuterium bond strength may also play a role. The main reason for this effect comes from the (anharmonic) coupling of the solvent with the solute. Buckingham studied the H-bond strength versus D-bond strength by quantum mechanical calculations many years ago and found that in aqueous systems, the D-bond strength is slightly stronger than the H-bond strength.30 The aqueous solvent isotope effect for acetate (and other Na-salts of aliphatic carboxylic acids) was first reported from a combination of heats of transfer measured by calorimetry and free energies of transfer obtained from emf measurements.31 The negative value at −34 cal mol−1 for the transfer free energy, ΔG0d←w, going from water to heavy water indicates that this process occurs spontaneously.31 A great variety of electrolytes and non-electrolytes was reported and summarized in ref. 32 and attempts to explain this phenomenon were put forward applying Gurney's potential.
3.4. The influence of acetate on the O–H stretching band of water
The influence of the solute, NaCH3CO2, on the water spectrum, especially in the O–H stretching region, should allow conclusions about the hydrophobic hydration of the apolar CH3 group of the acetate with H2O. The Raman O–H band profile of NaCH3CO2(aq) at 5.022 mol L−1 (Rw = 8.5) is displayed in Fig. 4, left panel and the infrared absorption spectrum from 400 to 4000 cm−1 of an aqueous 2.184 mol L−1 NaCH3CO2 solution (Rw = 22.9) with the one of neat water are presented in Fig. S3.† The complete concentration band profiles of three dilute to moderately concentrated aqueous NaCH3CO2 solutions are given in Fig. S4† together with the difference spectra of the OH band profiles of the dilute acetate solutions from which the water contributions were subtracted (see Fig. S5†). In the neat liquid, the isotropic O–H profile the water O–H band may be fitted with three Gaussian bands, two very broad and strong band contributions at 3211 cm−1 and 3405.6 cm−1 (also called the double band) and a shoulder at ∼3625 cm−1 which is also relatively broad (fwhh ∼ 125 cm−1). The band contribution at 3625 cm−1 is assigned to the weakly H-bonded H2O molecules of the water H-bond network while the band at 3211 cm−1 is assigned to represent the tetrahedrally H-bonded water molecules.33,34 The isotropic O–H Raman band profile of water of a concentrated NaCH3CO2 solution was fitted into three Gauss band contributions, as well, positioned at 3292 cm−1, 3455.5 cm−1 and a shoulder at ∼3618 cm−1 (fwhh = 120 cm−1). Except for the shift of the two broad and strong band contributions at 3211 and 3406 cm−1 for the isotropic O–H band profile, the shoulder at higher wavenumbers is almost unchanged (Fig. 8). A band from dangling H-bonds reported recently at 3672 cm−1 (ref. 35) showing a relatively narrow band width at 34 cm−1 could not be observed for the H-bonds around the methyl group in acetate solutions. The similarity of bulk water at higher wavenumbers in the O–H profile suggests that the water molecules (∼6 water10) are “clathrate-like” which means three out of four H-bonds are tangential oriented to the CH3 surface and one toward the bulk (Fig. 2 of ref. 36). The water structure around the small hydrophobic CH3 group is quite similar to the bulk water except for a somewhat slower water–water H-bond exchange kinetic which is only slightly retarded with respect to the bulk water.36 From theoretical and experimental methods, it turns out that the small CH3 group (in contrast to long alkyl chains) does not noticeable change the water structure, its connectivity, nor its H-bond strength.36,37 In other words, no enhanced hydrophobic hydration can be found around the methyl group of acetate. Furthermore, no signs of dangling O–H bands at ∼3670 cm−1 could be observed. However, in contrast to the NaCH3CO2(aq) in spectra of aqueous NaCF3CO2 solutions (see Fig. S6†), measured for comparison, from the dilute to concentrated solution stage a polarized band at 3671 cm−1 (fwhh = 34 cm−1) clearly indicates “dangling” OH bonds (see our results in Fig. S7†). These dangling OH bonds represent water molecules of the hydrophobic shell surrounding the strongly hydrophobic CF3 group and are quite similar to the ones in a water air or a water oil interface.38,393.5. Na+-acetate ion pairs
The question of the ion pairs formed in Na+ acetate solutions was addressed in our previous publication.12 However, the solutions of acetate-d3 in aqueous solution and heavy water may be used and studied again to shed light on this question. Raman bands of the CO2 group are significant markers for ion pair formation in solution. In conjunction with earlier DRS results, the nature of ion pairs in NaCH3CO2(aq) as a function of concentration may be highlighted. DR spectroscopy, a method used to yield information about the character of the ion pairs, reported a sequence of different species: outer–outer-sphere ion pairs, outer-sphere ion pairs but only a small number of contact ion pairs. The latter, if formed in solution should lead to large changes of the acetate bands in NaCH3CO2(aq) or a split of the modes into bound or “free” acetate which means non-associated. The formation of contact ion pairs/complexes formed in aqueous solutions was followed but no contact ion pairs could be verified. The advantage of studying the per-deuterated acetate ion, NaCD3CO2(aq), is that the symmetric stretching mode, νsCO2, at 1407.5 cm−1 may be observed undisturbed. In NaCH3CO2(aq), however, the symmetric stretch is obscured by the accidental overlap with two CH3 deformation modes as discussed above in Section 3.3. The νC–C mode and also νsCO2 impress as narrow and symmetrical bands in CD3CO2−(aq) (Fig. 8) and this indicates that no contact ion pairs of the form Na+·CH3CO2− (Na+·CD3CO2−) are formed because bands of the bound acetate will lead to separated bands or visible shoulders separate from the bands of the “free”, hydrated acetate ion. DRS investigations of acetate solutions, however, favored the formation of small amounts of contact ion pairs between Na+ and CH3CO2−,10 while in a subsequent paper the existence of such ion pairs was denied.11 Examples of divalent and even trivalent metal ion acetato complexes have been published over the years.40,414. Conclusions
Solutions of the sodium salts of CH3CO2− and CD3CO2− in water and heavy water were studied by Raman and infrared spectroscopy over a broad concentration range and in the wavenumber range from 40 cm−1 to 4200 cm−1. In the terahertz region the breathing mode of [Na(OH2)n]+ (n = 4, 5) was characterized at 189 cm−1 and the restricted translation mode of CH3CO2−⋯HOH a broad shoulder at 245 cm−1 (see also ref. 12). The acetate/acetate-d3 spectra were assigned according to pseudo Cs symmetry. Characteristic modes for acetate and acetate-d3 were identified. The two stretching modes of the CO2 group, νs and νas, at 1413.5 cm−1 and 1556 cm−1 respectively at 1407.5 cm−1 and 1547 cm−1 are characteristic. The stretching mode, νC–C for CH3CO2−(aq), appears at 928.4 cm−1 and the same stretching mode for CD3CO2−(aq) at 885.2 cm−1. In solutions of heavy water, however, the νC–C mode appears at 927.2 cm−1 and 882.8 cm−1 respectively. The vibrational isotope effect of the –CH3 (–CD3) group was observed and application of the Teller-Redlich product rule confirmed the frequency assignments.Coupling of the intramolecular modes are fairly extensive and therefore DFT cluster calculations on CH3CO2−·5H(D)2O and CD3CO2−·5H(D)2O were carried out in order to compare the measured spectra with the calculated ones. The geometrical parameters, such as bond length and bond angles of the acetate in solution state, were given.
The possibility of dangling νO–H bonds was discussed for aqueous NaCH3CO2 solutions. No evidence for such bonds could be found over the complete concentration range in these solutions in the infrared and Raman spectroscopy. However, in NaCF3CO2(aq) dangling νO–H bands were observed at 3670 cm−1. A deuterium solvent isotope effect was observed for the intramolecular acetate and acetate-d3 bands in water and heavy water. Finally, the formation process and the nature of the ion pairs formed between Na+ and acetate were discussed and it became clear that no contact ion pairs exist even in concentrated NaCH3CO2/NaCD3CO2 solutions.
References
- B. Hess and N. F. A. van der Vegt, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 13296–13300 CrossRef CAS PubMed.
- J. S. Uejio, C. P. Schwartz, A. M. Duffin, W. S. Drisdell, R. C. Cohen and R. J. Saykally, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 6809–6812 CrossRef CAS PubMed.
- I. D. Kuntz, J. Am. Chem. Soc., 1971, 93, 514–516 CrossRef CAS.
- R. Caminiti, P. Cucca, M. Monduzzi, G. Saba and G. Crisponi, J. Chem. Phys., 1984, 81, 543–551 CrossRef CAS PubMed.
- H. Naganuma, Y. Kameda, T. Usuki and O. Uemura, J. Phys. Soc. Jpn., 2001, 70(suppl. A), 356–358 Search PubMed.
- Y. Kameda, M. Sasaki, M. Yaegashi, K. Tsuji, S. Oomori, S. Hino and T. Usuki, J. Solution Chem., 2004, 33, 733–745 CrossRef CAS.
- G. D. Markham, M. Trachtman, C. L. Bock and C. W. Bock, J. Mol. Struct., 1998, 455, 239–256 CrossRef CAS.
- G. D. Markham, C. L. Bock and C. W. Bock, Struct. Chem., 1997, 8, 293–306 CrossRef CAS.
- A. Payaka, A. Tongraar and B. M. Rode, J. Phys. Chem. A, 2010, 114, 10443–10453 CrossRef CAS PubMed.
- H. M. A. Rahman, G. Hefter and R. Buchner, J. Phys. Chem. B, 2012, 116, 314–323 CrossRef CAS PubMed.
- H. M. A. Rahman and R. Buchner, J. Mol. Liq., 2012, 176, 93–100 CrossRef CAS PubMed.
- W. W. Rudolph, D. Fischer and G. Irmer, Dalton Trans., 2014, 43, 3174–3185 RSC.
- I. A. Heisler and S. R. Meech, Science, 2010, 327, 857–860 CrossRef CAS PubMed.
- W. W. Rudolph and G. Irmer, Appl. Spectrosc., 2007, 61, 1312–1324 CrossRef CAS PubMed.
- W. W. Rudolph, D. Fischer and G. Irmer, Appl. Spectrosc., 2006, 60, 130–144 CrossRef CAS PubMed.
- W. W. Rudolph, Z. Phys. Chem., 1996, 194, 73–90 CrossRef CAS.
- W. W. Rudolph, M. H. Brooker and C. C. Pye, J. Phys. Chem., 1995, 99, 3793 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez, and J. A. Pople, Gaussian 03, Revision C.02, Gaussian, Inc., Wallingford CT, 2004 Search PubMed.
- M. Cossi, G. Scalmani, N. Rega and V. Barone, J. Chem. Phys., 2002, 117, 43–54 CrossRef CAS PubMed.
- M. Meot-Ner and L. Wayne Sieck, J. Am. Chem. Soc., 1986, 108, 7525–7529 CrossRef CAS PubMed.
- Y. Kameda, K. Sugarwara, T. Usuki and O. Uemura, Bull. Chem. Soc. Jpn., 1998, 71, 2769–2776 CrossRef CAS.
- S. Varma and S. B. Rempe, Biophys. Chem., 2006, 124, 192–199 CrossRef CAS PubMed.
- R. Mancinelli, A. Botti, F. Bruni, M. A. Ricci and A. K. Soper, J. Phys. Chem. B, 2007, 111, 13570–13577 CrossRef CAS PubMed.
- S. S. Azam, T. S. Hofer, B. R. Randolf and B. M. Rode, J. Phys. Chem. A, 2009, 113, 1827–1834 CrossRef CAS PubMed.
- A. Bankura, V. Carnevale and M. L. Klein, J. Chem. Phys., 2013, 138, 014501–014510 CrossRef PubMed.
- D. C. McKean, Spectrochim. Acta, Part A, 1973, 29, 1559–1574 CrossRef.
- W. W. Rudolph and G. Irmer, unpublished results, TU Bergakademie Freiberg 2010.
- G. Herzberg, Molecular spectra and molecular structure, II. Infrared and Raman spectra of polyatomic molecules, Van Nostrand Reinhold Company, New York, 1945, p. 231 Search PubMed.
- O. Redlich, Z. Phys. Chem., Abt. B, 1935, 28, 371–382 Search PubMed.
- A. D. Buckingham and L. Fan-Chen, Int. Rev. Phys. Chem., 1981, 1, 253–269 CrossRef CAS.
- H. Snell and J. Greyson, J. Phys. Chem., 1970, 74, 2148–2152 CrossRef CAS.
- G. Jancso and W. A. Van Hook, Chem. Rev., 1974, 74, 689–750 CrossRef CAS p. 736.
- B. Auer, R. Kumar, J. R. Schmidt and J. L. Skinner, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 14215–14220 CrossRef CAS PubMed.
- B. M. Auer and J. L. Skinner, J. Chem. Phys., 2008, 128, 224511 CrossRef CAS PubMed.
- P. N. Perera, K. R. Fega, C. Lawrence, E. J. Sundstrom, J. Tomlinson-Phillips and D. Ben-Amotz, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 12230–12234 CrossRef CAS PubMed.
- M. Montagna, F. Sterpone and L. Guidoni, J. Phys. Chem. B, 2012, 116, 11695–11700 CrossRef CAS PubMed.
- J. Teixeira and A. Luzar, Physics of Liquid Water. Structure and Dynamics in Hydration Processes in Biology, ed. M. C. Bellissent-Funel, IOS Press, Ohmsha, NATO-Science Series, Series A, Life Science-305, 1999, pp. 35–68 Search PubMed.
- N. Ji, V. Ostroverkhov, C. S. Tian and Y. R. Shen, Phys. Rev. Lett., 2008, 100, 096102 CrossRef CAS.
- F. G. Moore and G. L. Richmond, Acc. Chem. Res., 2008, 41, 739–748 CrossRef CAS PubMed.
- G. B. Deacon and R. J. Phillips, Coord. Chem. Rev., 1980, 33, 227–250 CrossRef CAS.
- J. E. Tackett, Appl. Spectrosc., 1989, 43, 483–489 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra01156f |
| ‡ For the B3LYP/6-311++G(3df,2pd) level of theory lower DFT frequencies were obtained for the cluster [Na(H2O)6]+. However, this value is insecure because one imaginary frequency was obtained (saddle point). |
| § Note, that the numbering of the bands for CD3CO2− is different from the one for CH3CO2− because of the large isotope shift of the C–D modes (compare fundamental modes in Tables 2 and 3). |
| This journal is © The Royal Society of Chemistry 2015 |