Plasma-based dry reforming: improving the conversion and energy efficiency in a dielectric barrier discharge†
R. Snoeckx*a,
Y. X. Zengb,
X. Tu*b and
A. Bogaertsa
aResearch Group PLASMANT, Department of Chemistry, University of Antwerp, Antwerp, Belgium. E-mail: ramses.snoeckx@uantwerpen.be; xin.tu@liverpool.ac.uk
bDepartment of Electrical Engineering and Electronics, University of Liverpool, Liverpool L69 3GJ, UK
First published on 19th March 2015
Abstract
Dry reforming of methane has gained significant interest over the years. A novel reforming technique with great potential is plasma technology. One of its drawbacks, however, is energy consumption. Therefore, we performed an extensive computational study, supported by experiments, aiming to identify the influence of the operating parameters (gas mixture, power, residence time and “frequency”) of a dielectric barrier discharge plasma on the conversion and energy efficiency, and to investigate which of these parameters lead to the most promising results and whether these are eventually sufficient for industrial implementation. The best results, in terms of both energy efficiency and conversion, are obtained at a specific energy input (SEI) of 100 J cm−3, a 10–90 CH4–CO2 ratio, 10 Hz, a residence time of 1 ms, resulting in a total conversion of 84% and an energy efficiency of 8.5%. In general, increasing the CO2 content in the gas mixture leads to a higher conversion and energy efficiency. The SEI couples the effect of the power and residence time, and increasing the SEI always results in a higher conversion, but somewhat lower energy efficiencies. The effect of the frequency is more complicated: we observed that the product of frequency (f) and residence time (τ), being a measure for the total number of micro-discharge filaments which the gas molecules experience when passing through the reactor, was critical. For most cases, a higher number of filaments yields higher values for conversion and energy efficiency. To benchmark our model predictions, we also give an overview of measured conversions and energy efficiencies reported in the literature, to indicate the potential for improvement compared to the state-of-the art. Finally, we identify the limitations as well as the benefits and future possibilities of plasma technology.
Introduction
The conversion of the main greenhouse gases, CO2 and CH4, into value added chemicals and liquid fuels is considered as one of the main challenges for the 21st century.1,2 The combined reforming of both CH4 and CO2, i.e., dry reforming of methane (DRM), has therefore gained significant interest over the years because of its (possible) environmental impact.3,4 Its main advantages over other reforming processes are the use of CO2 as both a carbon source and oxidizing agent and the production of syngas (H2/CO) in a ratio which is easily controllable. The main disadvantage for implementing catalytic DRM on an industrial scale is its inherent carbon deposition, which leads to catalyst poisoning.5 Nevertheless, as stated by Mikkelsen et al.6 ‘The formation of synthesis gas by dry reforming of methane could provide a substantial use for CO2 from industrial and natural sources. This capture provides a renewable, inexhaustible carbon source and could also provide a means for the continued use of derived carbon fuels in an environmental friendly and carbon neutral way.’ As a result, the interest for alternative (non-conventional) reforming technologies grew quickly and one of the alternatives which is considered to have great potential in this area is plasma technology.7The advantage of non-thermal plasmas, compared to the classical catalytic process, is that the gas can remain near room temperature while being “activated” by electron impact excitation, ionization and dissociation reactions. Furthermore, higher conversions and selectivities can be obtained without problems of carbon deposition.8 The energy required for sustaining a plasma is provided by electricity, which at first seems to limit its use as a greenhouse gas mitigation technology, since in general producing electricity results in CO2 emissions. The type of plasma which is currently most often used for DRM (and gas conversion in general) is the dielectric barrier discharge (DBD). Tao et al.8 calculated that for every mole CO2 reformed in a DBD, one mole CO2 would be emitted if the electricity came from methane combustion. Furthermore, in our previous work9 we calculated that the energy efficiency of plasma-based DRM would need to achieve a theoretical energy efficiency of at least ∼60% to be competitive with classical DRM.
Nevertheless, plasma technology is attracting a lot of attention because of several advantages over conventional gas conversion techniques. One of those advantages is closely related to the worldwide transition to renewable energy sources, such as solar and wind energy. The large scale adoption of these renewable energy sources poses a challenge for efficient storage and easy transport of the electricity produced (i.e., during peak moments on the grid). While storage in batteries is possible, it is less efficient than chemical storage in fuels.10 Such fuels, often referred to as carbon neutral fuels or solar fuels, offer a much higher gravimetric and volumetric energy storage capacity, they have much higher energy densities than electrical storage techniques and they match the existing worldwide liquid fuel infrastructure.6,10 As such, the current transition to renewable energy sources does not only give plasma processes a clean electricity source, but because of the high operation flexibility, i.e., plasmas can be turned on and off quickly, they are very suitable for storing intermittent sustainable energy in a chemical form. More specifically, the syngas produced in this way can then be chemically processed into chemicals and fuels, for example by using the conventional Fischer–Tropsch process.11
However, plasma technology is not the only player in this field and one of its drawbacks, especially of a DBD, is the energy consumption, which is currently still too high for industrial application, even when using sustainable energy sources.8,9 Therefore, in the present paper, we perform an extensive computational optimization study for a DBD, based on a model that we developed and validated before.9 Moreover, some new experiments are performed to support the model in this broader parameter range. The aim of this study is to identify the influence of the operating parameters of a DBD for DRM and to investigate which of these parameters are most promising in terms of energy efficiency and conversion and whether this is eventually sufficient for industrial implementation or whether different plasma set-ups (i.e., packed-bed DBD7,12 or so-called warm plasmas7,8,13–16) should be pursued.
Description of the model
0D chemical kinetics model
The model used in this work to describe the plasma chemistry is a zero-dimensional (0D) kinetic model, called Global_kin, developed by Kushner and co-workers.17 This model calculates the time-evolution of the species densities, based on the production and loss terms defined by the chemical reactions. An energy balance equation calculates the electron temperature, which is used by the Boltzmann equation module to calculate the rate coefficients of the electron impact reactions. For a more detailed description of the model, we refer to our previous work.9Plasma chemistry included in the model
The chemistry set used in this model was developed and experimentally validated in our previous work.9 It considers 62 different species, which react with each other in 121 electron impact reactions, 87 ion reactions and 290 neutral reactions. Their corresponding rate coefficients and the references where these data were adopted from are listed in the ESI of our previous work.9Description of a filamentary DBD setup in the model
DBDs typically operate in the filamentary regime, consisting of a large number of micro-discharge filaments,18 which present themselves in the electrical current waveform as many short peaks. Describing these filaments in a plasma model is not straightforward, because of their distribution in time and space. Nonetheless, including a realistic description of these filaments is indispensable to obtain a realistic description of the plasma chemistry. One might argue that a 0D model seems unfit for this task, since it only allows simulating the plasma behavior as a function of time, and not as a function of space. However, this temporal behavior can easily be translated into a spatial behavior, by means of the gas flow, allowing us to mimic the filamentary behavior by simulating a large number of micro-discharge pulses as a function of time. This approach has already proven to be applicable for a variety of conditions and gas mixtures.9,19–22 A more detailed description of this method can be found in our previous work.9Calculation of conversion and energy efficiency
To identify the most energy efficient operating conditions, we varied the following parameters in a wide range: gas composition, specific energy input (SEI), gas residence time and “frequency” (see below). The critical calculation output in this assessment will be the total conversion and the energy efficiency of the process.The conversion of CH4 and CO2 is defined as:
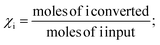 | (1) |
The total conversion can then be written as:
| χTotal = fraction CO2·χCO2 + fraction CH4·χCH4 | (2) |
Furthermore, the energy efficiency is determined as follows:
 | (3) |
 | (4) |
Explanation of the parameters varied in this study
The parameters varied in this study are as follows:- CH4–CO2 gas composition (%): 90–10, 75–25, 50–50, 25–75, 10–90;
- SEI (J cm−3): 0.01, 0.1, 1, 10, 100;
- Residence time (s): 0.001, 0.01, 0.1, 1, 10, 100;
- Frequency (kHz): 0.01, 0.1, 1, 10, 100.
Hence, it is clear that for every gas composition 150 different combinations are possible, bringing the total number of numerically investigated cases to 750.
Note that the values of these parameters are chosen based on typical values reported in literature, i.e., a residence time ranging from 1 till 100 s, a SEI going from 1 till 100 J cm−3 and a frequency in the order of 1 to 100 kHz are commonly reported.8,9,23–28 However, besides these typical values, we also want to explore new regions of these parameters, which are to date not yet reported, e.g., a residence time of 0.001 s, coupled with an SEI of 0.1 J cm−3, which might be pursued for micro-reactors.29,30 This is exactly the strength of computer simulations to go beyond the classical conditions and to predict whether new conditions could be more promising, and thus whether experimentally the construction of new reactor types or power set-ups should be pursued.
For the interpretation of the calculation results it is important to understand how the variation of these parameters relates to experiments. The gas composition, SEI and residence time can be directly compared to experiments (through the experimental gas flow rate, reactor volume and power). However, the variation of the “frequency” is a more complex story, which can be looked at from two different angles. (a) On one hand, if we assume that the average number of filaments that occur during each half cycle of the applied voltage is constant, varying the frequency is a way to control the total number of filaments that occur during a certain residence time of the gas, and thus the energy deposited in each filament (keeping the total applied power constant). In this case, the “frequency” directly corresponds to the experimental frequency of the applied voltage. (b) Another way to interpret the “frequency” is when the number of filaments that occur during each half cycle is not constant but varies with the operating conditions. Then, a higher (or lower) “frequency” corresponds to a larger (or smaller) number of filaments during each half cycle, with a lower (or higher) energy deposition per filament. To our knowledge, it is not yet known from literature whether (and how) the number of filaments per half cycle changes for a CH4–CO2 gas mixture, depending on the operating conditions. It is well possible that for certain conditions or experimental set-ups assumption (a) is valid, while for other conditions, case (b) is valid, or even a combination of both. This meaning of the “frequency” should thus be kept in mind in the following sections, but in any case, the frequency is directly proportional to the total number of filaments for a fixed gas residence time.
Experimental
Plasma reactor
The experiments are carried out in a coaxial DBD reactor. A stainless steel mesh (ground electrode) is wrapped over the outside of a quartz tube with an outer and inner diameter of 22 and 19 mm, respectively, while a stainless steel rod with an outer diameter of 14 mm is placed in the center of the quartz tube and used as high voltage electrode. The length of the discharge region is 90 mm with a discharge gap of 2.5 mm. CH4 and CO2 are used as feed gases with a variable total flow rate of 25–200 ml min−1 and a CO2–CH4 molar ratio from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 to 9
9 to 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The DBD reactor is supplied by a high voltage AC power supply with peak-to-peak voltage of 10 kV and frequency of 50 Hz. The Q–U Lissajous method is used to calculate the discharge power.
1. The DBD reactor is supplied by a high voltage AC power supply with peak-to-peak voltage of 10 kV and frequency of 50 Hz. The Q–U Lissajous method is used to calculate the discharge power.
Product analysis
The feed and product gases are analyzed by a two-channel gas chromatograph (Shimadzu GC-2014) equipped with a flame ionization detector (FID) and a thermal conductivity detector (TCD). The GC is calibrated for a wide range of gases using reference gas mixtures (Air Liquide).Experimental parameter range
Although our model was validated before,9 several additional experiments were performed for this work, to assure that the model, and especially the chemistry set, behave in a realistic manner for conditions beyond the previously validated range.9 However, as the total parameter range under investigation is quite large, still only a small part of it could be probed experimentally. This is exactly the aim of our simulations, i.e., by identifying the effects of the above mentioned parameters and subsequently searching for the optimal conditions, we can save a lot of work on expensive and time consuming experiments.The experimental parameters selected for this additional model validation are listed in Table 1 for a fixed applied frequency of 50 Hz. This parameter selection is limited, because it is based on one experimental setup, i.e., reactor (volume), power supply, mass flow controllers, and this of course restricts the experimental range that is possible. The range could have been made wider if experiments would have been performed with different set-ups, but this would have introduced more unknown variables and effects, which we want to avoid. To allow a one-to-one comparison between model and experiments, we performed additional simulations besides the parameter range already mentioned, to mimic the exact experimental conditions.
| Gas mixture CH4–CO2 (%) | Residence time (s) | Power (W) | SEI (J cm−3) |
|---|---|---|---|
| 90–10 | 32.57 | 15 | 36 |
| 7.5 | 18 | ||
| 75–25 | 32.57 | 15 | 36 |
| 7.5 | 18 | ||
| 50–50 | 32.57 | 15 | 36 |
| 7.5 | 18 | ||
| 16.29 | 15 | 18 | |
| 7.5 | 9 | ||
| 10.86 | 15 | 12 | |
| 7.5 | 6 | ||
| 8.14 | 15 | 9 | |
| 7.5 | 4.5 | ||
| 4.07 | 15 | 4.5 | |
| 7.5 | 2.25 | ||
| 25–75 | 32.57 | 15 | 36 |
| 7.5 | 18 | ||
| 10–90 | 32.57 | 15 | 36 |
| 7.5 | 18 |
Results and discussion
First, we will show the comparison between the model and experimental results, explaining the effect of the various parameters on the conversion and energy efficiency. Subsequently, the general influence of these parameters will be discussed in more detail, as observed for the entire simulation range, to reveal the optimum conditions. Finally, we will compare our model predictions with literature and we will identify the limitations as well as the benefits and future possibilities.In this study, we focus only on the total conversion and resulting energy efficiency, and not on the selectivity of the formed products. However, in general, the following trends regarding the product distributions were observed. At high CO2 contents, the main products are the molecules typically formed in CO2 splitting (i.e., CO and O2), and also a fair amount of H2O. The reason of its formation was explained in our previous work.22 Upon increasing the CH4 content, on the other hand, the concentration of the classical dry reforming products (i.e., H2, C2H2, C2H4, C2H6, C3H6, C3H8) starts to increase, at the expense of the CO2 splitting products. Changing the frequency or residence time only had a small effect on the absolute concentrations of the formed products, but no significant effect on the product distributions.
Comparison between model and experiments
 | ||
| Fig. 2 Calculated and experimental total conversion (a) and energy efficiency (b) as a function of residence time, for a 50–50 CH4–CO2 mixture, and a plasma power of 7.5 and 15 W. | ||
It is clear that both in the experiments and the simulations the total conversion is about a factor two higher for a power of 15 W compared to 7.5 W, at the same residence time, which is logical because a higher power yields more (and higher energy) electrons, which can activate the gas and thus initiate the conversion. For the energy efficiency, the trend is less clear. For a residence time ≤10 s a higher power yields a slightly higher energy efficiency, whereas for a higher residence time the effect is opposite, but not significant.
Furthermore, when the power is kept constant, the total conversion increases with increasing residence time (which is also straightforward) and the energy efficiency shows the opposite decreasing trend. The latter is most obvious in the calculation results. It follows directly from eqn (3) and (4) above: a higher residence time corresponds to a lower flow rate, and thus a higher SEI, at constant power (cf. eqn (4)). If the SEI increases more than the conversion, upon increasing residence time, this results in a drop in the energy efficiency (cf. eqn (3)).
The effect of the residence time and power can also be combined by plotting the total conversion and energy efficiency as a function of the SEI, as shown in Fig. 3, for a plasma power of 7.5 and 15 W and corresponding residence times as reported in Table 1. Note that the model is again applied in a broader range than could be investigated in the experiments, i.e., four extra points were added for an SEI of 1 and 100 J cm−3, for both power values.
 | ||
| Fig. 3 Calculated and experimental total conversion (a) and energy efficiency (b) as a function of SEI, for a 50–50 CH4–CO2 mixture, and a plasma power of 7.5 and 15 W. | ||
It is clear that the SEI is the major determining factor for the conversion and energy efficiency, as it combines the effect of power and residence time (see eqn (4)). Indeed, at the same SEI, increasing the power (thus lowering the residence time) does not affect the total conversion, which remains practically the same at constant SEI. The energy efficiency shows somewhat more variations, when varying the power or residence time, at constant SEI, but these variations are still within a few %.
In general, we may conclude that the calculation and experimental results are again in reasonable agreement, so that we can be confident about the predictive nature of our model, and use it to investigate the effect of the operating conditions in a wider range, beyond what is typically accessible for (standard) experiments.
Model predictions in a wider parameter range
We have systematically studied the effect of all individual parameters, by means of 750 simulations (see above), of which the detailed graphs can be found in the ESI.† In this section, we will show the combined effects, and summarize the general results by means of a few graphs, to elucidate the optimum conditions both in terms of conversion and energy efficiency.It is clear that a larger amount of CO2 leads to a higher total conversion and energy efficiency. This trend is certainly true for the best conditions (solid lines, full symbols). For example, with increasing CO2 content, the maximum achieved energy efficiency goes from 11.4 to 15.1%. For the worst conditions, the same trend can be observed for the low SEI values, but for the higher SEI values (10 and 100 J cm−3), the frequency and residence time start to play a role, and depending on the product of both, a slightly different trend can be observed. These trends are elaborated in detail in the ESI (see Fig. S1–S10).† Summarized, in general, the higher total conversion and energy efficiency at larger CO2 contents is attributed to the O atoms formed by electron impact dissociation of CO2, which react very effectively with the H atoms originating from electron impact dissociation of CH4. As shown in our kinetic analysis9 the conversion of CH4 is normally limited by the fast backward reaction, CH3 + H → CH4, but when more O atoms are available, this reaction is of minor importance compared to the reaction O + H → OH. Thus, by limiting the backward reaction, the conversion of CH4 rises dramatically with increasing CO2 content, leading to a higher total conversion.
Therefore, in Fig. 5 the conversion and energy efficiency are plotted as a function of the total number of micro-discharge filaments experienced by the gas molecules, for a 50–50 gas mixture and for the different values of SEI investigated (see legend). The graphs for the other gas mixtures can be found in the ESI (S11–S15).†
Keeping in mind that for every gas mixture 150 different simulations are performed (see above), this means that Fig. 5 contains 30 data points per SEI value (i.e., per color symbol). As there are only 7 different combinations of the product τ·f, it means that several data points (more or less) coincide with each other. Hence, as anticipated above, all cases with different values of frequency and residence time, but with the same product τ·f, yield almost identical values for conversion and energy efficiency, at a fixed SEI. Thus, it becomes clear that, for a given gas mixture, both the product τ·f and the SEI are the main underlying factors determining the plasma chemistry and linking the SEI, residence time and frequency all together.
It is clear from Fig. 5 that, at fixed SEI, increasing the number of micro-discharge filaments leads to a slightly higher conversion and energy efficiency, except for the highest number (200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000), where the opposite trend is seen, and for the highest SEI values of 10 and 100 J cm−3, where an initial decrease is observed for a low number of filaments. As mentioned above, all gas mixtures show the same general trends, except in the case of 90% CO2 for the highest SEI values of 10 and 100 J cm−3 and for 75% for an SEI of 100 J cm−3, where a lower number of filaments leads to a higher total conversion.
000), where the opposite trend is seen, and for the highest SEI values of 10 and 100 J cm−3, where an initial decrease is observed for a low number of filaments. As mentioned above, all gas mixtures show the same general trends, except in the case of 90% CO2 for the highest SEI values of 10 and 100 J cm−3 and for 75% for an SEI of 100 J cm−3, where a lower number of filaments leads to a higher total conversion.
Since in the model the energy is divided equally over all micro-discharge filaments, increasing the number of filaments results in a lower energy deposited per filament. It seems that for most cases (except the ones mentioned before) a higher number of filaments, but with lower energy, yields higher values for conversion and energy efficiency, compared to a lower number of filaments, but with more energy deposited per filament. In general, the effect of the total number of filaments seems more important for the energy efficiency than the SEI (except between 10 and 100 J cm−3), while the total conversion seems less affected by the number of filaments than by the SEI, which was explained above.
Comparison with literature and critical analysis of the limitations and possibilities of plasma technology
As mentioned above, the highest total conversion (84.2%) is obtained at the highest SEI (100 J cm−3), and a CO2 content of 90%, yielding an energy efficiency of 8.5%. The highest energy efficiency (15.1%), on the other hand, is found for the lowest SEI (0.01 J cm−3) and again a CO2 content of 90%, but this corresponds to a total conversion of only 0.015%. Furthermore, both the total conversion and energy efficiency increase with increasing CO2 content, while increasing the SEI results in a higher total conversion but a lower energy efficiency, illustrating the trade-off between both. Considering all operating conditions investigated, it is clear that the best overall results (i.e., combination of conversion and energy efficiency) are obtained for the highest SEI and typically for a large total number of filaments, obtained through a residence time of 10–100 s, combined with a frequency of 100–10 kHz, respectively, except for 90 and 75% CO2, where a lower number of filaments (obtained through a short residence time of 0.001–0.01 s independent of the frequency), or a higher residence time, combined with a low frequency of 0.1 kHz, led to the best results. Table 2 summarizes the best results obtained for the different gas mixtures.| CH4–CO2 gas mixture | Conversion | Energy efficiency |
|---|---|---|
| 90–10 | 36.9% | 3.7% |
| 75–25 | 44.7% | 4.5% |
| 50–50 | 53.5% | 5.4% |
| 25–75 | 67.0% | 6.7% |
| 10–90 | 84.2% | 8.5% |
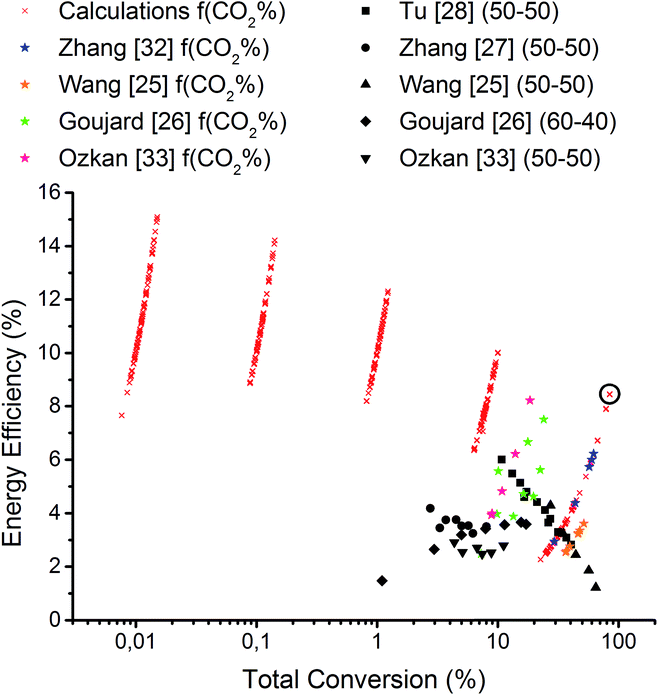
To compare our results with the current state-of-the-art from literature, Fig. 6 illustrates the various experimental data for energy efficiency vs. total conversion, obtained from literature,25–28,32,33 in comparison with our simulation results, for all conditions investigated. The experimental conditions from literature, and their corresponding results for conversion and energy efficiency, are summarized in Table 3.
| SEI (J cm−3) | Frequency (kHz) | CH4–CO2 (%) | Conversion (%) | Energy efficiency (%) | References | ||
|---|---|---|---|---|---|---|---|
| Lower | Upper | Lower | Upper | ||||
| a Experiments diluted in N2.b Experiments diluted in Ar. | |||||||
| 7–23 | 2.5 | 50–50 | 2.8 | 8.1 | 4.2 | 3.5 | 27 |
| 7–48 | Pulsed | 60–40a | 1.1 | 17.2 | 1.5 | 3.6 | 26 |
| 15–40 | 19.5 | 50–50b | 4.4 | 11.1 | 2.9 | 2.8 | 33 |
| 18–144 | 30–40 | 50–50 | 10.8 | 40.5 | 6.0 | 2.8 | 28 |
| 64–532 | 15.67 | 50–50 | 27.2 | 64.6 | 4.3 | 1.2 | 25 |
| 22.5 | 19.5 | 80–20b | 8.9 | — | 4 | — | 33 |
| 20–80b | — | 18.4 | — | 8.2 | |||
| 25–40 | Pulsed | 60–40a | 7.26 | 19.7 | 2.5 | 4.6 | 26 |
| 40–60a | 10.1 | 24 | 5.6 | 7.5 | |||
| 100 | 25 | 83–17 | — | 62 | — | 6.2 | 32 |
| 34–66 | 29.3 | — | 2.9 | — | |||
| 143 | 15.67 | 83–17 | — | 46 | — | 3.2 | 25 |
| 17–83 | 36.3 | — | 2.6 | — | |||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| Packed bed DBD | |||||||
| 12 | 1–100 | 50–50 | 27 | 22.6 | 12 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| Microwave at atm pressure | |||||||
| 18 | Pulsed | 60–40 | 70 | 39.0 | 8 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| Gliding arc | |||||||
| 11.4 | 10–20 | 50–50 | 35.5 | 31.2 | 13 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| Gliding arc | |||||||
| 1.32–3.96 | 0.05 | 50–50 | 9.8 | 13.9 | 74.6 | 35.2 | 14 |
It is clear from Fig. 6 and Table 3 that the operating conditions, especially the SEI values, have a large influence on the obtained conversion and energy efficiency. Most experiments are performed for SEI values between 10 and 100 J cm−3, and they give rise to conversions and energy efficiencies in the same order as predicted by our simulations. Especially the agreement with experimental results obtained for different CH4–CO2 mixtures (denoted by the colored stars) is remarkable. The results of Goujard et al.26 en Ozkan et al.33 show exactly the same trend for the effect of gas mixture (i.e., higher conversion and energy efficiency at higher CO2 content). Furthermore, for a SEI of 100 J cm−3 our calculations perfectly match with the results of Zhang et al.32 Finally, the results of Wang et al.25 indicate a maximum conversion and energy efficiency at 50% CO2, which can also be explained by our model, because for the high SEI under consideration, the applied frequency (15.67 kHz) yields good results for low CO2 content, but at high CO2 content, lower frequencies would be required.
Besides the good correlation between our model predictions and the literature results, it is also obvious from Fig. 6 that by careful selection of the operating conditions, higher values of energy efficiency (at fixed conversion) or higher conversions (for a given energy efficiency) could be achieved in our model than the values currently reported in literature. Indeed, at a conversion of 10%, the best energy efficiencies found in literature are about 5%, whereas our calculations predict values up to 10%, by careful selection of the frequency, residence time and gas mixture. Furthermore, a conversion of 84.2% with 8.5% energy efficiency, as obtained for 90% CO2 content (see circle in Fig. 6) is also significantly better than the available experimental data. Also for the other gas mixing ratios, our “best results” (in terms of combination of conversion and energy efficiency; cf. Table 2) are better than the results reported to date in literature (see Table 3).
As mentioned above, in general a compromise needs to be made between the energy efficiency and the total conversion, since the conversion increases but the energy efficiency drops with higher SEI. Nevertheless, this trade-off is less severe than expected. Increasing the SEI over five orders of magnitude results in almost the same rise in conversion, while the energy efficiency drops only by 44–67% (depending on the gas mixture). This clearly demonstrates that it is not interesting to work at low SEI values to optimize the energy efficiency, since the gain in energy efficiency is negligible compared to the enormous loss in conversion.
In order to be competitive with current technologies and to reduce end-of-pipe gas separation costs, a conversion of 50–80%, comparable with current DRM plants, would be preferred. This is achievable with a DBD, as is clear from Fig. 6, but it requires an SEI in the order of 100 J cm−3, resulting in energy efficiencies of 8.5 to 3.7%, depending on the gas mixture.
Conclusions
In this paper we have studied the influence of the operating parameters (gas mixture, power, residence time and “frequency”) of a dielectric barrier discharge plasma on the conversion and energy efficiency, to investigate which of these parameters lead to the most promising results and whether these are eventually sufficient for industrial implementation.The obtained conversion of 84% with an energy efficiency of 8.5% can be considered as the best results in terms of both energy efficiency and conversion. The parameters leading to this result were an SEI of 100 J cm−3, a 10–90 CH4–CO2 ratio, 10 Hz, a residence time of 1 ms. In general we found that increasing the amount of CO2 in the mixture led to an increase in conversion and energy efficiency. While increasing the SEI, which couples the effect of the power and residence time, only resulted in an increased conversion, but saw a slight decrease in energy efficiency. The most complicated effect was that of the frequency, in the end it was unravelled that it was rather the product of frequency (f) and residence time (τ), i.e. the total number of micro-discharge filaments which the gas molecules experience when passing through the reactor, which was critical here. For most cases passing a higher number of filaments (with less energy per filament) yielded higher values for conversion and energy efficiency.
Furthermore, the maximum (theoretical) energy efficiency predicted in this study lies between 11.4 and 15.1%, depending on the CH4–CO2 ratio, which clearly demonstrates that there is still room for improvement for the experiments reported to date, by careful selection of the operating conditions. However, when comparing this maximum theoretical value with the maximum theoretical energy efficiency obtained for classical thermal DRM, i.e., around 60%, it is clear that when the energy efficiency is the “key performance indicator”, a classical DBD is not competitive. On the other hand, its ease of use (incl. its fast start-up and switch-off, which can save a lot of energy when DRM is combined with other technologies such as fuel cells), its scale-up possibilities as demonstrated for ozone generation and gas cleaning18 and its capability to convert peak currents from renewable energy sources will probably still give it an advantage over the classical DRM process. Nevertheless, keeping in mind that other alternative techniques can also take advantage of the same peak renewable energy,6 it is clearly more interesting from a combined economic and ecologic point of view to focus on other plasma reactor types, for which already higher energy efficiencies have been obtained (see Table 3). This includes microwave discharges,8 gliding arcs8,13,14 and packed bed DBDs.12 In the latter case, a DBD is filled with a packing, yielding higher energy efficiencies, i.e., up to a factor 12, as demonstrated already for air pollution control.34 Moreover, this packing can be made of catalytic material, yielding plasma-catalysis.7,35 This has the additional advantage that the selectivity towards value-added chemicals and fuels (such as methanol, formaldehyde, formic acid, etc.) can greatly be improved, making plasma technology very promising for the dry reforming of methane.
Acknowledgements
The authors acknowledge financial support from the IAP/7 (Inter-university Attraction Pole) program ‘PSI-Physical Chemistry of Plasma-Surface Interactions’, financially supported by the Belgian Federal Office for Science Policy (BELSPO), as well as the Fund for Scientific Research Flanders (FWO). This work was carried out in part using the Turing HPC infrastructure at the CalcUA core facility of the Universiteit Antwerpen, a division of the Flemish Supercomputer Center VSC, funded by the Hercules Foundation, the Flemish Government (department EWI) and the University of Antwerp. Financial support of this work by the UK Engineering and Physical Sciences Research Council (EPSRC) CO2Chem Network and Knowledge Exchange (KE) fund of the University of Liverpool is also gratefully acknowledged.Notes and references
- Contribution of Working Group I to the Fourth Assesment Report of the Intergovernmental Panel on Climate Change, Climate Change 2007: The Physical Science Basis, ed. S. Solomon, D. Qin, M. Manning, M. Marquis, K. Averyt, M. M. B. Tignor, H. L. Miller and Z. Chen, Cambridge University Press, New York, 2007 Search PubMed.
- J. H. Lunsford, Catal. Today, 2000, 63, 165–174 CrossRef CAS.
- A. T. Ashcroft, A. K. Cheetham, M. L. H. Green and P. D. F. Vernon, Nature, 1991, 352, 225–226 CrossRef CAS.
- M. C. J. Bradford and M. A. Vannice, Catal. Rev.: Sci. Eng., 1999, 41, 1–42 CAS.
- J. R. H. Ross, Catal. Today, 2005, 100, 151–158 CrossRef CAS PubMed.
- M. Mikkelsen, M. Jørgensen and F. C. Krebs, Energy Environ. Sci., 2010, 3, 43 CAS.
- S. Samukawa, M. Hori, S. Rauf, K. Tachibana, P. Bruggeman, G. Kroesen, J. C. Whitehead, A. B. Murphy, A. F. Gutsol, S. Starikovskaia, U. Kortshagen, J.-P. Boeuf, T. J. Sommerer, M. J. Kushner, U. Czarnetzki and N. Mason, J. Phys. D: Appl. Phys., 2012, 45, 253001 CrossRef.
- X. Tao, M. Bai, X. Li, H. Long, S. Shang, Y. Yin and X. Dai, Prog. Energy Combust. Sci., 2011, 37, 113–124 CrossRef CAS PubMed.
- R. Snoeckx, R. Aerts, X. Tu and A. Bogaerts, J. Phys. Chem. C, 2013, 117, 4957–4970 CAS.
- Z. Jiang, T. Xiao, V. L. Kuznetsov and P. P. Edwards, Philos. Trans. R. Soc., A, 2010, 368, 3343–3364 CrossRef CAS PubMed.
- M. E. Dry, Catal. Today, 2002, 71, 227–241 CrossRef CAS.
- Q. Wang, Y. Cheng and Y. Jin, Catal. Today, 2009, 148, 275–282 CrossRef CAS PubMed.
- A. Indarto, J. Choi, H. Lee and H. Song, Energy, 2006, 31, 2986–2995 CrossRef CAS PubMed.
- X. Tu and J. C. Whitehead, Int. J. Hydrogen Energy, 2014, 39, 9658–9669 CrossRef CAS PubMed.
- A. Fridman, Plasma chemistry, Cambridge University Press, New York, 2008 Search PubMed.
- A. Gutsol, A. Rabinovich and A. Fridman, J. Phys. D: Appl. Phys., 2011, 44, 274001 CrossRef.
- R. Dorai, K. Hassouni and M. J. Kushner, J. Appl. Phys., 2000, 88, 6060–6071 CrossRef CAS PubMed.
- U. Kogelschatz, Plasma Chem. Plasma Process., 2003, 23, 1–46 CrossRef CAS.
- R. Snoeckx, M. Setareh, R. Aerts, P. Simon, A. Maghari and A. Bogaerts, Int. J. Hydrogen Energy, 2013, 38, 16098–16120 CrossRef CAS PubMed.
- R. Aerts, T. Martens and A. Bogaerts, J. Phys. Chem. C, 2012, 116, 23257–23273 CAS.
- R. Aerts, X. Tu, W. Van Gaens, J. C. Whitehead and A. Bogaerts, Environ. Sci. Technol., 2013, 47, 6478–6485 CAS.
- R. Aerts, R. Snoeckx and A. Bogaerts, Plasma Process. Polym., 2014, 11, 985–992 CrossRef CAS.
- C. Xu and X. Tu, J. Energy Chem., 2013, 22, 420–425 CrossRef CAS.
- R. Aerts, W. Somers and A. Bogaerts, ChemSusChem, 2015, 8, 702–716 CrossRef CAS PubMed.
- Q. Wang, B.-H. Yan, Y. Jin and Y. Cheng, Plasma Chem. Plasma Process., 2009, 29, 217–228 CrossRef CAS PubMed.
- V. Goujard, J.-M. Tatibouët and C. Batiot-Dupeyrat, Appl. Catal., A, 2009, 353, 228–235 CrossRef CAS PubMed.
- X. Zhang and M. S. Cha, J. Phys. D: Appl. Phys., 2013, 46, 415205 CrossRef.
- X. Tu and J. C. Whitehead, Appl. Catal., B, 2012, 125, 439–448 CrossRef CAS PubMed.
- J. H. Lozano-Parada and W. B. Zimmerman, Chem. Eng. Sci., 2010, 65, 4925–4930 CrossRef CAS PubMed.
- U. Kogelschatz, Contrib. Plasma Phys., 2007, 47, 80–88 CrossRef CAS.
- T. Kozák and A. Bogaerts, Plasma Sources Sci. Technol., 2014, 23, 045004 CrossRef.
- Y. Zhang, Y. Li, Y. Wang, C. Liu and B. Eliasson, Fuel Process. Technol., 2003, 83, 101–109 CrossRef CAS.
- A. Ozkan, T. Dufour, G. Arnoult, P. De Keyzer, A. Bogaerts and F. Reniers, J. CO2 Util., 2015, 9, 74–81 CrossRef CAS PubMed.
- H. L. Chen, H. M. Lee, S. H. Chen and M. B. Chang, Ind. Eng. Chem. Res., 2008, 47, 2122–2130 CrossRef CAS.
- E. C. Neyts and A. Bogaerts, J. Phys. D: Appl. Phys., 2014, 47, 224010 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: The ESI contains (a) an overview of the detailed experimental and computational results, used for the model validation; as a function of the CH4–CO2 ratio, the residence time and the SEI. (b) All graphs and a more extensive description of the influence regarding gas ratio in the entire range of conditions. See DOI: 10.1039/c5ra01100k |
| This journal is © The Royal Society of Chemistry 2015 |