Transport properties of g-BC3 and t-BC3 phases
A. H. Reshak*ab
aNew Technologies – Research Centre, University of West Bohemia, Univerzitni 8, 306 14 Pilsen, Czech Republic. E-mail: maalidph@yahoo.co.uk; Tel: +420 777729583
bCenter of Excellence Geopolymer and Green Technology, School of Material Engineering, University Malaysia Perlis, 01007 Kangar, Perlis, Malaysia
First published on 27th March 2015
Abstract
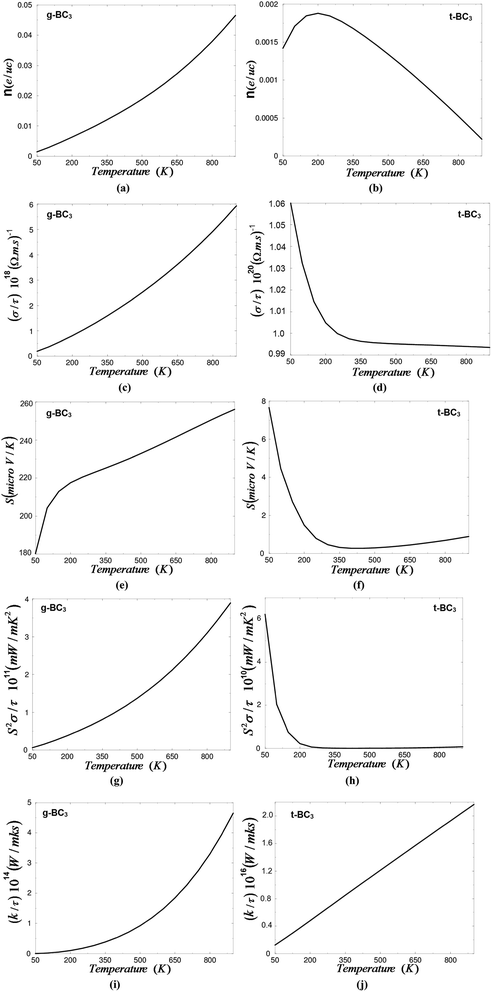
The calculated electronic band structure shows that the g-BC3 phase is a narrow band gap semiconductor constructed from an ABAB,…, stacking sequence. Whereas t-BC3 is a metallic phase constructed from a sandwich-like metal-insulator lattice from an alternately stacking sequence of a metallic CBC block and an insulating CCC block. The electronic transport coefficients of the g-BC3 and t-BC3 phases are obtained with the aid of the semi-classical Boltzmann theory and the rigid band model based on density functional theory within the recently modified Becke–Johnson potential (mBJ). The semiconductor phase (g-BC3) exhibits a linearly dependent charge carrier concentration and electrical conductivity with temperature, whereas for the t-BC3 phase the charge carrier concentration is increased with increasing temperature up to 200 K, then a rapid decrease occurs upon increasing the temperature. The electrical conductivity of t-BC3 shows the highest value at 50 K then a rapid decrease occurs upon increasing the temperature up to 250 K, and it stays roughly constant above this temperature. The Seebeck coefficient of the g-BC3 and t-BC3 phases shows that these materials exhibit p-type conduction and the g-BC3 phase exhibits a higher Seebeck coefficient than the t-BC3 phase. The g-BC3 phase exhibits an almost linearly dependent power factor with temperature. Whereas the power factor of the t-BC3 phase shows a very high value at low temperature then drops to the lower value at 200 K. Above this temperature the power factor of t-BC3 becomes zero along the whole temperature range. It has been found that the g-BC3 phase shows a higher power factor than that of the t-BC3 phase. The electronic thermal conductivity of g-BC3 exponentially increases with increasing temperature. It has a zero value at 50 K and the highest value 4.6 × 1014 (W m−1 K−1 s−1) at 900 K. t-BC3 exhibits linearly dependent electronic thermal conductivity with temperature. At low temperature (50 K) the electronic thermal conductivity of t-BC3 is about 0.15 × 1016 (W m−1 K−1 s−1) while it has a value of about 2.1 × 1016 (W m−1 K−1 s−1) at 900 K. It is clear that the g-BC3 phase exhibits lower electronic thermal conductivity than the t-BC3 phase.
1. Introduction
Thermoelectric power generators can convert heat into electricity which is a good alternative solution for energy and environmental problems.1 Ever since this discovery, extensive studies have been done on several materials to enhance their thermoelectric properties for technological applications.2–11 The development of novel thermoelectric materials has attracted a great deal of interest due to their significant potential applications ranging from clean energy to photon sensing devices. The efficient thermoelectric materials can be classified into three types; complex crystals, alloys and nano-crystals.12 They can provide a significant contribution to solve the global sustainable energy problems. The thermoelectric materials may also be used as solid-state Peltier coolers12 in addition to generating electricity from waste heat. Efficient thermoelectric materials should possess high figure of merit (ZT = S2σT/κ), to achieve this we need to optimize the Seebeck coefficient (S) and electrical conductivity (σ) and lower the thermal conductivity (κ). In recent years thermoelectric materials have played an important role in global sustainable energy solutions.13–15The growing demand for unusual thermoelectric materials motivated us to comprehensively investigate the transport properties of boron-rich diamond materials. There is great interest in boron-rich diamond materials due to their excellent chemical and physical properties. It has been found that these materials possess high mechanical strength, high hardness, high thermal conductivity, high electron and hole mobility, high chemical inertness, and low mass density.16,17 These superhard materials are of great demand for numerous applications for instances in electronic industry, solar cells production and mechanical machining. Several researchers focus their attention on finding novel superhard materials with good conductivity.17–24 Combining between superhard and metallic properties are of great interest for the creation multifunctional materials with potential applications as metal-insulator junction, metal-insulator devices and photonic devices.20 It has been reported that the t-BC3 phase is stable with space group P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2m,21 and exhibits metallic behavior at ambient and high pressures. While g-BC3 is a semiconductor at both ambient and high pressures and stable with space group Cmcm.17 Liu et al.17 predicted the synthesis of the t-BC3 phase from g-BC3 phase at high pressure and they confirm the stability of both phases at the space group P
2m,21 and exhibits metallic behavior at ambient and high pressures. While g-BC3 is a semiconductor at both ambient and high pressures and stable with space group Cmcm.17 Liu et al.17 predicted the synthesis of the t-BC3 phase from g-BC3 phase at high pressure and they confirm the stability of both phases at the space group P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2m and Cmcm, respectively. Also it was reported that a superconductivity was found in boron-doped diamond synthesized at high temperature and high pressure25 and increasing the dopant concentrations led to enhance the superconductivity.26–28
2m and Cmcm, respectively. Also it was reported that a superconductivity was found in boron-doped diamond synthesized at high temperature and high pressure25 and increasing the dopant concentrations led to enhance the superconductivity.26–28
From above, it is clear that the previous experimental and theoretical work are devoted on the synthesis of BC3, study the crystal structure, electronic properties, elastic properties with very few reports on the linear optical properties, all the previous calculations are done using non-full potential methods. Therefore, due to a lack information regarding the thermoelectric properties of the superhard metallic g-BC3 and t-BC3 compounds, and as natural extended to our recent work on g-BC3 and t-BC3 (ref. 29) we have addressed ourselves for comprehensive theoretical calculations based on the density functional theory (DFT) within all-electron full potential method and the semi-classical Boltzmann theory as incorporated in BoltzTraP code30 to calculate the thermoelectric properties of g-BC3 and t-BC3 phases. In this calculation we have employed the all-electron full potential linear augmented plane wave plus local orbitals (FPLAPW + lo) method. First-principles calculation is one strong and useful tool to predict the crystal structure and its properties related to the electron configuration of a material before its synthesis.31–34
2. Details of calculations
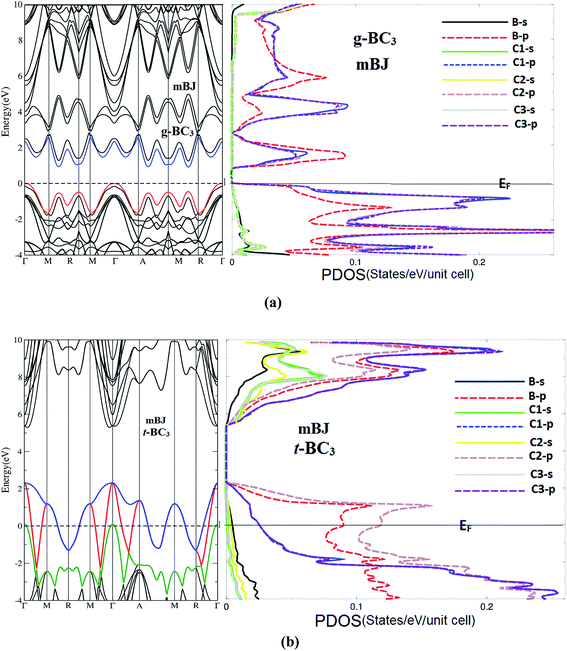
The graphitic-like g-BC3 crystallizes in orthorhombic space group Cmcm, with ABAB,…, stacking sequence as illustrated in Fig. 1(a). In the unit cell of g-BC3 the structural parameters are a = 8.834 Å, b = 5.104 Å and c = 7.071 Å, the B atom is located at (0.167, 0.823, 0.25), C1 at (0.159, 0.323, 0.25), C2 at (0.792, 0.562, 0.25) and C3 at (0.421, 0.585, 0.25).17 The boron-rich diamond t-BC3 crystallizes in tetragonal space group P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2m with eight atoms per unit cell as illustrated in Fig. 2(a–d). The structural parameters of t-BC3 are a = b = 3.513 Å and c = 3.871 Å, the B atom is situated at (0.5, 0.0, 0.5), C1 at (0.0, 0.0, 0.0), C2 at (0.25, 0.25, 0.229) and C3 at (0.5, 0.5, 0.0).17 In both (t-BC3 and g-BC3) phases the B atom connected to three C atoms in different configurations.
2m with eight atoms per unit cell as illustrated in Fig. 2(a–d). The structural parameters of t-BC3 are a = b = 3.513 Å and c = 3.871 Å, the B atom is situated at (0.5, 0.0, 0.5), C1 at (0.0, 0.0, 0.0), C2 at (0.25, 0.25, 0.229) and C3 at (0.5, 0.5, 0.0).17 In both (t-BC3 and g-BC3) phases the B atom connected to three C atoms in different configurations.
Using the all-electron full potential linear augmented plane wave plus local orbitals (FPLAPW + lo) method as implemented in WIEN2k code35 within generalized gradient approximation (PBE-GGA),36 the geometry of t-BC3 and g-BC3 are relaxed by minimizing the forces acting on each atom. The structures are totally relaxed when the forces on each atom reach values less than 1 mRy per a.u. From the relaxed geometry the ground state properties of t-BC3 and g-BC3 are calculated within the local density approximation (CA-LDA),37 PBE-GGA and Engel–Vosko generalized gradient approximation (EVGGA).38 To overcome the DFT-LDA/GGA band gap's underestimation we have introduced EVGGA. It is well known that EVGGA able to reproduce better exchange potential at the expense of less agreement in the exchange energy. This approach yields better band splitting compared to LDA and GGA but still underestimated the band gap therefore, we have used the recently modified Becke–Johnson potential (mBJ).39 The mBJ, a modified Becke–Johnson potential, allows the calculation of band gaps with accuracy similar to the very expensive GW calculations.39 It is a local approximation to an atomic “exact-exchange” potential and a screening term. We should mention that hybrid functionals40,41 are a correct way of solving the under-estimated band gaps that they observe in the boron/carbon structures.
The plane-wave cuttoff, defined by the product of the smallest atomic sphere radius times the magnitude of the largest reciprocal-lattice vector (RMT × KMAX), is taken to be equal to 8. In the muffin-tin (MT) spheres the potential and charge density are expanded in spherical harmonics with lmax = 8 and nonspherical components up to lmax = 6. In the interstitial region the potential and the charge density are represented by Fourier series. Self-consistency is obtained using 800 ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) points in the irreducible Brillouin zone (IBZ). We have calculated the transport properties using 12
points in the irreducible Brillouin zone (IBZ). We have calculated the transport properties using 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000 ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) points in the IBZ. The convergence of the total energy in the self-consistent calculations is taken with respect to the total charge of the system with a tolerance 0.0001 electron charges. We have used the semi-classical Boltzmann theory as incorporated in BoltzTraP code30 to calculate the thermoelectric properties like carrier concentration (n), Seebeck coefficient (S), electrical conductivity (σ/τ), electronic thermal conductivity (κe/τ), and the electronic power factor (S2σ/τ) as a function of temperature at certain value of the chemical potential. The constant relaxation time approximation and the rigid band approximation were used in the calculations.30 BoltzTrap code depends on a well tested smoothed Fourier interpolation to obtain an analytical expression of bands. This is based on the fact that the electrons contributing to transport are in a narrow energy range due to the delta-function like Fermi broadening. For such a narrow energy range the relaxation time is nearly the same for the electrons. The accuracy of this method has been well tested earlier, and the method actually turns out to be a good approximation.42 The temperature dependence of the energy band structure is ignored. The formula of the transport coefficients as a function of temperature and chemical potential are given somewhere else.30,43 To gain high thermoelectric efficiency, it is important that the material possess high electrical conductivity, large Seebeck coefficient and low thermal conductivity.44
points in the IBZ. The convergence of the total energy in the self-consistent calculations is taken with respect to the total charge of the system with a tolerance 0.0001 electron charges. We have used the semi-classical Boltzmann theory as incorporated in BoltzTraP code30 to calculate the thermoelectric properties like carrier concentration (n), Seebeck coefficient (S), electrical conductivity (σ/τ), electronic thermal conductivity (κe/τ), and the electronic power factor (S2σ/τ) as a function of temperature at certain value of the chemical potential. The constant relaxation time approximation and the rigid band approximation were used in the calculations.30 BoltzTrap code depends on a well tested smoothed Fourier interpolation to obtain an analytical expression of bands. This is based on the fact that the electrons contributing to transport are in a narrow energy range due to the delta-function like Fermi broadening. For such a narrow energy range the relaxation time is nearly the same for the electrons. The accuracy of this method has been well tested earlier, and the method actually turns out to be a good approximation.42 The temperature dependence of the energy band structure is ignored. The formula of the transport coefficients as a function of temperature and chemical potential are given somewhere else.30,43 To gain high thermoelectric efficiency, it is important that the material possess high electrical conductivity, large Seebeck coefficient and low thermal conductivity.44
3. Results and discussion
3.1. Salient features of the electronic band structures
We recall the main features of the electronic band structure dispersion and the density of states (DOS) of g-BC3 and t-BC3 phases which are calculated within mBJ approach as shown in Fig. 1(a) and (b). The electronic band structure and DOS exhibit that g-BC3 phase is a narrow band indirect band gap semiconductor, the calculated band gap is about 0.9 eV using mBJ which is much better than our EVGGA (0.7 eV) and the previous results (0.66 eV) using LDA,45 it is well known that LDA underestimated the band gap by around 30–40%. To the best of our knowledge, there are no experimental data for the energy band gap is available in literature to make a meaningful comparison. We would like to mention here that in our previous works46–48 we have calculated the energy gap using mBJ on several systems whose energy gap are known experimentally. In these calculations we find very good agreement with the experimental data. Thus, we believe that our calculated band gap within mBJ reported in this paper would produce very accurate and reliable results. Future experimental work will testify our calculated results.The t-BC3 is a metallic phase where theB-2p and C-2p empty orbitals of CBC block and the C-2p empty orbitals of CCC block cuts the Fermi level (EF). It has been found that the top of the B-2p and C-2p empty orbitals is about 2.4 eV above EF in reasonable agreement with previous results (2.28 eV (ref. 21) and 2.7 eV (ref. 17)).
3.2. Transport properties
Fig. 3(a) and (b) demonstrate the charge carriers concentration of g-BC3 and t-BC3 phases as a function of temperature at a certain value of the chemical potential (μ). For the semiconductor phase (g-BC3) the charge carrier concentration is almost linearly dependent on temperature. The lowest value charge carriers concentration is about 0.002 e per uc occurs at 50 K, whereas the highest value is about 0.046 e per uc at 900 K. The high value of the carrier concentration is attributed to the fact that firstly, in g-BC3 phase, the B-2p and C-2p orbitals lie near EF resulting in large density of states near EF and hence increase the scattering which lead to lower the carrier mobility, the other reason for lower the carrier mobility is the non-parabolic conduction bands near EF (see Fig. 1). Secondly, due to the electro-negativity difference between C (2.55) and B (2.04) atoms therefore, there exists a strong covalent bonding between B–C and C–C atoms, generally covalent bond is more favorable for the transport of carriers compared with ionic component.49 The charge carriers concentration of t-BC3 phase is about 0.0014 e per uc at 50 K (Fig. 3(b)). Then the carriers concentration increases with increasing the temperature to reach its maximum of about 0.0018 e per uc at 200 K. Above this temperature the carriers concentration rapidly decreases with rising the temperature to reach about 0.00024 e per uc at 900 K.
The low values of the charge carrier concentration in t-BC3 phase is attributed to the fact that since the B-2p and C-2p empty orbitals of CBC block and the C-2p empty orbitals of CCC block cuts the Fermi level, this cause to intensifying lowering the carrier concentration. The total carrier concentration is defined as the difference between the hole and the electron concentration. The electron and holes carrier concentration are define as:50
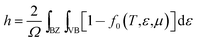 | (1) |
 | (2) |
In the above equations, the integral is performed over the Brillouin Zone (BZ) as well as over conduction band (CB) for electrons (e) or valence band (VB) for holes (h).
The electrical conductivity of g-BC3 and t-BC3 phases as a function of temperature are presented in Fig. 3(c) and 3(d). It has been found that the electrical conductivity of g-BC3 phase increases (almost) linearly with increasing the temperatures that is attributed to the fact that g-BC3 possess high carriers concentration which increases linearly with rising the temperatures. The electrical conductivity value is about 0.2 × 1018 (Ω m s)−1 at 50 K and 5.9 × 1018 (Ω m s)−1 at 900 K. Whereas the electrical conductivity of t-BC3 phase show the highest value of about 1.06 × 1020 (Ω m s)−1 at 50 K, then a rapid decreases occur with increasing the temperature up to 250 K and then stays roughly constant above this temperature to reach its lowest value of about 0.994 × 1020 (Ω m s)−1 at 900 K. It is clear that the t-BC3 exhibit higher electrical conductivity than g-BC3 phase that is attributed to the fact that the carriers of t-BC3 phase possess higher mobility than that of g-BC3 phase. The relaxation time is taken to be direction independent and isotropic.51
4. Conclusions
The electronic transport coefficients of g-BC3 and t-BC3 phases are evaluated by using the semi-classical Boltzmann theory and rigid band model based on the density functional theory within the full potential linear augmented plane wave plus local orbitals (FPLAPW + lo) method in a scalar relativistic version as embodied in the WIEN2k code. The exchange and correlation potential was treated within the modified Becke–Johnson potential which allows the calculation of band gaps with accuracy similar to the very expensive GW calculations. It has been found that the charge carrier concentration and electrical conductivity of g-BC3 phases are systematically increases with increasing the temperature, while for t-BC3 phase the charge carrier concentration increases with the temperature up to 200 K then a rapid decreases occurs and the electrical conductivity rapidly decreases with increasing the temperature up to 250 K and then stays roughly constant. The calculation explored that both of g-BC3 and t-BC3 phases are a p-type conductions. The calculation show that the g-BC3 phase exhibit higher Seebeck coefficient, higher power factor and low electronic thermal conductivity than t-BC3 phase. Based on the above results we expected that the g-BC3 phase exhibit better thermoelectric properties than that of t-BC3 phase.Acknowledgements
The result was developed within the CENTEM project, reg. no. CZ.1.05/2.1.00/03.0088, cofunded by the ERDF as part of the Ministry of Education, Youth and Sports OP RDI programme and, in the follow-up sustainability stage, supported through CENTEM PLUS (LO1402) by financial means from the Ministry of Education, Youth and Sports under the National Sustainability Programme I. Computational resources were provided by MetaCentrum (LM2010005) and CERIT-SC (CZ.1.05/3.2.00/08.0144) infrastructures.References
- H. Wang, W. Chu and H. Jin, Comput. Mater. Sci., 2012, 60, 224 CrossRef CAS.
- K. P. Ong, D. J. Singh and P. Wu, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 115110 CrossRef.
- D. Parker and D. J. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 233206 CrossRef.
- D. Parker, M.-H. Du and D. J. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 245111 CrossRef.
- D. J. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 195217 CrossRef.
- K. P. Ong, D. J. Singh and P. Wu, Phys. Rev. Lett., 2010, 104, 176601 CrossRef PubMed.
- G. B. Wilson-Short, D. J. Singh, M. Fornari and M. Suewattana, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 035121 CrossRef.
- D. J. Singh and D. Kasinathan, J. Electron. Mater., 2007, 36, 736 CrossRef CAS.
- D. J. Singh, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 085110 CrossRef.
- D. J. Singh, Mater. Res. Soc. Symp. Proc., 2008, 1044, U02–U05 Search PubMed.
- D. J. Singh, US Pat. 8,487,178, 2013.
- H. A. Rahnamaye Aliabad, M. Ghazanfari, I. Ahmad and M. A. Saeed, Comput. Mater. Sci., 2012, 65, 509 CrossRef CAS.
- F. J. DiSalvo, Science, 1999, 285, 703–706 CrossRef CAS PubMed.
- T. M. Trit, Science, 1996, 272, 1276–1277 CrossRef.
- L. E. Bell, Science, 2008, 321, 1457–1461 CrossRef CAS PubMed.
- P. V. Zinin, L. C. Ming, I. Kudryashov, N. Konishi and S. K. Sharma, J. Raman Spectrosc., 2007, 38, 1362 CrossRef CAS.
- Z. Liu, J. He, J. Yang, X. Guo, H. Sun, H.-T. Wang, E. Wu and Y. Tian, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 172101 CrossRef.
- R. Hoffmann, R. Hoffmann, T. Hughbanks, M. Kertesz and P. H. Bird, J. Am. Chem. Soc., 1983, 105, 4831 CrossRef CAS.
- C. J. Pickard, V. Milman and B. Winkler, Diamond Relat. Mater., 2001, 10, 2225 CrossRef CAS.
- J. L. He, L. C. Guo, E. Wu, X. G. Luo and Y. J. Tian, J. Phys.: Condens. Matter, 2004, 16, 8131 CrossRef CAS.
- M. M. Ali, A. K. M. A. Islam, M. Aftabuzzaman and F. Parvin, J. Sci. Res., 2010, 2(2), 203–213 CAS.
- P. V. Zinin, L. C. Ming, S. K. Sharma, S. M. Hong, Y. Xie, T. Irifune and T. Shinmei, J. Phys.: Conf. Ser., 2008, 121, 062002 CrossRef.
- H. Liu, Q. Li, L. Zhu and Y. Ma, Phys. Lett. A, 2011, 375, 771–774 CrossRef CAS.
- L. Li, W. X. Li, D. Han, S. Wei Xin, Y. Yang, W. Zhou and Y. Feng Lu, Mater. Sci. Forum, 2013, 749, 551 CrossRef.
- E. A. Ekimov, V. A. Sidorov, E. D. Bauer, N. N. Mel'nik, N. J. Curro, J. D. Thompson and S. M. Stishov, Nature, 2004, 428, 542 CrossRef CAS PubMed.
- Y. Ma, J. S. Tse, T. Cui, D. D. Klug, L. Zhang, Y. Xie, Y. Niu and G. Zou, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 014306 CrossRef.
- Y. Takano, T. Takenouchi, S. Ishii, S. Ueda, T. Okutsu, I. Sakaguchi, H. Umezawa, H. Kawarada and M. Tachiki, Diamond Relat. Mater., 2007, 16, 911 CrossRef CAS.
- K. W. Lee and W. E. Pickett, Phys. Rev. Lett., 2004, 93, 237003 CrossRef PubMed.
- A. H. Reshak, Phys. Chem. Chem. Phys., 2015, 17, 8006 RSC.
- G. K. H. Madsen and D. J. Singh, BoltzTraP. A code for calculating band-structure dependent quantities, Comput. Phys. Commun., 2006, 175, 67–71 CrossRef CAS.
- A. H. Reshak and S. Auluck, RSC Adv., 2014, 4, 37411 RSC.
- A. H. Reshak, RSC Adv., 2014, 4, 39565 RSC.
- M. Jamal, N. Kamali Sarvestani, A. Yazdani and A. H. Reshak, RSC Adv., 2014, 4, 57903 RSC.
- A. H. Reshak, RSC Adv., 2015, 5, 22044 RSC.
- P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka and J. Luitz, WIEN2k, An augmented plane wave plus local orbitals program for calculating crystal properties, Vienna University of Technology, Austria, 2001 Search PubMed.
- J. P. Perdew, S. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- W. Kohn and L. J. Sham, Phys. Rev. A, 1965, 140, 1133 CrossRef.
- E. Engel and S. H. Vosko, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 13164 CrossRef CAS.
- F. Tran and P. Blaha, Phys. Rev. Lett., 2009, 102, 226401 CrossRef PubMed.
- B. G. Janesko, J. Chem. Phys., 2011, 134, 184105 CrossRef PubMed.
- B. M. Wong and J. G. Cordaro, J. Phys. Chem. C, 2011, 115, 18333 CAS.
- D. Wang, L. Tang, M. Q. Long and Z. G. Shuai, J. Chem. Phys., 2009, 131, 224704 CrossRef PubMed.
- T. J. Scheidemantel, C. Ambrosch-Draxl, T. Thonhauser, J. V. Badding and J. O. Sofo, Transport coefficients from first-principles calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68(6), 125210 CrossRef.
- G. J. Snyder and E. S. Toberer, Complex thermoelectric materials, Nat. Mater., 2008, 7, 105–114 CrossRef CAS PubMed.
- A BC3 monolayer in an unrelaxed graphite structure with dBC = dCC = 1.42 Å is calculated to be an indirect-gap semiconductor with a negligibly small gap. This gap opens upon structural relaxation. In general, the true gap is larger than the calculated LDA gap, as discussed, e.g., by M. S. Hybertsen and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 5390 CrossRef CAS.
- A. H. Reshak, H. Huang, H. Kamarudin and S. Auluck, J. Appl. Phys., 2015, 117, 085703 CrossRef.
- A. H. Reshak, O. V. Parasyuk, A. O. Fedorchuk, H. Kamarudin, S. Auluck and J. Chyský, J. Phys. Chem. B, 2013, 117, 15220–15231 CAS.
- A. H. Reshak, I. V. Kityk, O. V. Parasyuk, H. Kamarudin and S. Auluck, J. Phys. Chem. B, 2013, 117, 2545–2553 CrossRef CAS PubMed.
- G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114 CrossRef CAS PubMed.
- A. H. Reshak and W. Khan, J. Alloys Compd., 2014, 591, 362–369 CrossRef CAS.
- B. Xu, X. Li, G. Yu, J. Zhang, S. Ma, Y. Wang and L. Yi, J. Alloys Compd., 2013, 565, 22–28 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2015 |