In situ study of the annealing process of a polyethylene cast film with a row-nucleated crystalline structure by SAXS
R. J. Xua,
X. D. Chena,
Q. Caia,
C. B. Chena,
Y. F. Linb,
C. H. Lei*a and
L. B. Lib
aGuangdong Provincial Key Laboratory of Functional Soft Condensed Matter, School of Materials and Energy, Guangdong University of Technology, Guangzhou 510006, PR China. E-mail: Lch528@gdut.edu.cn
bNational Synchrotron Radiation Lab and College of Nuclear Science and Technology, CAS Key Laboratory of Soft Matter Chemistry, University of Science and Technology of China, Hefei 230051, PR China
First published on 13th March 2015
Abstract
An in situ annealing process of a polyethylene cast film with a row-nucleated crystalline structure was followed using a SAXS setup equipped with a temperature-controlling unit. The annealing temperatures were set at 105 °C, 115 °C and 125 °C, respectively. It was found that after annealing for 7200 s, the long period, crystalline thickness, the real amorphous layer thickness and diffuse transition layer thickness were increased, whereas the linear crystallinity didn't show a pronounced change. Compared with those at 105 °C and 115 °C, annealing at 125 °C resulted in an apparent increase of the long period and crystalline thickness, as well as the crystalline thickening rate. During the initial annealing stage, the crystalline thickness was increased apparently. After annealing for 1800 s, the crystalline thickness versus annealing time curve showed a wave-like shape, due to the occurrence of melting and recrystallization behavior, which could not be observed during the early annealing stage. The initial crystalline thickness increase was mainly due to the crystallization of some tie chains in the amorphous region, as well as a small transformation of the diffuse transition layer into the crystalline region. The crystalline orientation degree based on the width of the SAXS patterns was improved apparently when the annealing temperature was around the maximum crystalline temperature. This work clarified the increase of crystalline thickness induced by annealing a polyethylene film with a row-nucleated crystalline structure.
Introduction
Based on the thermal-induced phase separation mechanism, a high-density-polyethylene (HDPE) microporous membrane has been successfully fabricated and used in the field of Li-ion batteries as a separator.1 Due to the use of solvents such as dichloromethane to remove the liquid paraffin to form micropores, this method brings about some environmental problems. Compared with this, the melt-stretching method using pure PE as a raw material will show no such problem. During the process, there are three main consecutive stages: (1) production of the precursor film with a row-nucleated lamellar morphology, (2) annealing of the film to thicken the lamellae, and (3) stretching of the film at low temperature to create voids and then stretching at high temperature to enlarge the pores.2,3 After these stages, the stretched films are heat-set to improve their dimensional stability.It has been reported that microporous membrane cannot be obtained without annealing. It is believed that annealing first removes defects in the crystalline structure and then increases the lamellae thickness.4 The annealing temperature, annealing time, and tension level are three main annealing technology parameters.5–8 In our previous work,9 the influence of annealing time on the structure and properties of HDPE microporous membrane was studied. It was found that compared with that without annealing, the porosity of membrane annealed at 125 °C for 2 h was increased from 43% to 63% and the corresponding Gurley value (characterizing the air permeability property, the lower the Gurley value is, the better the air permeability) was decreased from 430 s to 250 s. It can be seen that annealing shows pronounced influence on the properties of stretched microporous membrane. However, it is still unclear as to the mechanism of the microstructural changes during annealing of HDPE film with row-nucleated crystalline structure.
For annealing polypropylene film with row-nucleated crystalline structure, it was found that compared with the precursor film, the significant change after annealing was the appearance of a low temperature endotherm plateau (i.e. annealing peak) in the differential scanning calorimetry (DSC) curves.10–13 As to its origin, most works attributed to the crystallization of some chains among the amorphous region-secondary crystallization during annealing. In our recent work,14 based on the temperature-modulated differential scanning calorimetry (TMDSC) results and small-angle X-ray scattering (SAXS) analysis, it was found that except for secondary crystallization, the melting and recrystallization behavior also occurred during annealing. The annealing induced the difference of lamellae structure: the initial lamellae were stabilized through melting and recrystallization, at the same time some weak secondary crystals were formed which could be stretched to disappear and converted to initial pores.
But in the DSC curves of annealed HDPE film with row-nucleated crystalline structure, no such endotherm plateau was observed. It was found that with increasing annealing temperature, the melting point moved to higher temperature.7,9 Based on Thomson equation, the lamellae thickness was deduced to be increased by annealing and at the same time the crystallinity was improved. Lee7 attributed the increase of lamellae thickness to the crystallization of some tie chains-secondary crystallization. We want to know except for secondary crystallization, are there any other crystalline phenomena occurring and contributing to the increase of crystalline thickness during annealing. In the 1960s, Peterlin,15–18 Statton19 and Sanchez20,21 et al. have made detailed work about the influence of annealing process on the crystalline structure including long period increase,18 recrystallization19 and crystal thickening20 for PE single crystal or spherulites. In recent years, some studies focus on the effect of structure parameters including molecular weight, branching degree and cross-linking on the crystallization process.22–25 But till now, there are few works to study the annealing process in oriented PE crystalline structure.
SAXS setup equipped with a temperature-controlling unit can be used to in situ follow the crystalline structure change during thermal treatment of polymers.26–29 It can directly give the information of long period and structure periodicity. In this article, to clarify what have happened during annealing of HDPE cast film with row-nucleated crystalline structure, in situ SAXS setup equipped with a temperature-controlling unit was used to follow the annealing process at different temperatures. The crystalline structure change during annealing was investigated.
Experimental
Material
HDPE resin with a density of 0.955 g cm−3 (under ASTM D 792) and a melt flow rate value of 0.35 g/10 min (under ASTM D 1238 conditions of 190 °C and 2.16 kg) from Yanshan petrochemical company, China, was used. The melting peak point (Tm) and the maximum crystallization temperature (Tc) obtained from DSC (PerkinElmer DSC 7, Massachusetts, United States) at a rate of 10 °C min−1, were 130 °C and 114 °C, respectively. The weight-average molecular weight and polydispersity index, measured using a GPC (Viscotek model 350) at 135 °C and 1,2,4-trichlorobenzene (TCB) as a solvent, were about 447 kg mol−1 and 8.66, respectively.Precursor cast film preparation
The precursor film was prepared by cast extrusion through a T-slot die followed by stretching and thermal-setting. During extrusion, the uniaxial (machine direction, MD) stretching was applied to the HDPE melt, which resulted in the oriented crystalline structures. The die temperature was set at 210 °C and a draw ratio of 120 was applied. The draw ratio was determined by the take-up speed, since the extrudate velocity at the exit of the die was constant. The films were produced at a chill roll temperature of 90 °C.Small-angle X-ray scattering
The in situ annealing process was carried out using temperature-controlling unit appended in the SAXS setup.26 The SAXS measurements were made using an in-house setup with a 30 W micro X-ray source (Incoatec, GmbH), providing highly parallel beam (divergence about 1 mrad) of monochromatic Cu Kα radiation (λ = 0.154 nm). The scattering intensity was collected by a multiwire proportional chamber detector (Bruker Hi-star) with a resolution of 1024 × 1024 pixels (pixel size of 105 μm). The distance between sample and detector was 2280 mm. The scattering signals were collected every 10 s. The annealing temperatures were set at 105 °C, 115 °C and 125 °C, respectively.Differential scanning calorimetry (DSC)
To characterize the annealing effect, the precursor films were also annealed at 125 °C in a hot oven for 1800 s, 3600 s and 7200 s, respectively. A TA Instrument temperature modulated DSC Q2000 (TA, USA) was used for TMDSC studies. The measurements were performed with a heating rate of 2 °C min−1 having a period of 60 s and amplitude of 0.5 °C. In order to maximize the signals, a specimen weighting around 8 mg was used. All the measurements were performed under dry nitrogen atmosphere.Results and discussion
In situ SAXS results during annealing at temperature of 105 °C
Fig. 1 gives the two-dimensional SAXS pattern, one-dimensional scattering intensity distribution along the machine direction as well as corresponding correlation function during annealing at 105 °C. The scattering intensity was integrated along the equatorial direction using sector integration. Before integration, the instrument background was subtracted considering sample absorption. For comparison, the SAXS pattern of precursor cast film is also included. For the cast film, only equational scattering signal appears. The weak meridian signal comes from the beam stop. This indicates that higher oriented crystalline structure is formed during cast process. After annealing, the SAXS pattern shape does not show much difference. In the one-dimensional scattering intensity distribution, no multiplication q2 to I(q) is performed because of the anisotropic orientation of the lamellae in the samples, where q is the scattering vector
q = 4π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ θ/λ
| (1) |
| L = 2π/q | (2) |
But the scattering curves at different annealing time are very close. Compared with that of precursor film, the scattering intensity only shows a little increase.
The one-dimensional correlation function, K(r), is a powerful tool in revealing the morphological parameters of the crystalline-amorphous two-phase systems and is obtained from indirect Fourier transformation of the scattering function. As indicated by the arrows in Fig. 1(c), the curve gives various structural parameters, e.g. the crystalline long period (Lc) and amorphous region thickness (La), according to the well-known methodology proposed by Strobl et al.32 It must be mentioned that it is impossible to decide whether it is the amorphous or the crystalline thickness that is read out from the correlation function without prior knowledge of the crystallinity. In the present study, the degree of crystallinity is higher than 0.5 (the crystallinity of cast film is 58.5% calculated from DSC testing) ensuring the assignment of the smaller value obtained from the correlation function to the average thickness of the amorphous region. The crystalline thickness (Lc) can be obtained with the relation
| Lc = L − La | (3) |
The long period obtained from the correlation function is identical with that obtained from the intensity distribution data I(q) using Bragg's law directly. But in fact, in the semi-crystalline polymer system, the diffuse transition layer exists between the crystalline phase and the amorphous phase. So, in the case of diffuse transition boundaries, L can be expressed as
| L = L′a + Lc + 2 × Ld | (4) |
 | (5) |
Fig. 2 gives the plots of Porod's law and the schematic of fit line within high q region. With increasing annealing time, the slope of the fit line within high q region gradually transforms to positive deviation. In other words, the slope of the fitted line is a positive number. This change is mainly due to the fluctuations of electron densities and thermal motion.
 | ||
| Fig. 2 Plots of Porod's law (a), the schematic of fit line within high q region (b) and the plot of Porod's law after subtracting the background intensity and the fit line in the high q region (c). | ||
In order to calculate the diffuse transition layer thickness, the Porod's law can be written as:36
 | (6) |
 | (7) |
| L′a = La − 2 × Ld | (8) |
Fig. 3 gives the long period (L), crystalline thickness (Lc), real amorphous thickness (L′a) and diffuse transition layer thickness (Ld) as well as linear crystallinity during annealing at 105 °C. Annealing induces the increase of long period. After annealing for 7200 s, the long period is increased from 27.5 nm without annealing to 30.0 nm, by about 9%. For the precursor film, the crystalline thickness is 16.1 nm, the real amorphous thickness is 9.3 nm and the diffuse transition layer thickness is 1.05 nm. After annealing for 100 s, 1800 s, 3600 s and 7200 s, the crystalline thicknesses are 16.9 nm, 17.5 nm, 17.6 nm and 17.6 nm, respectively. The real amorphous thicknesses are 10.8 nm, 10.5 nm, 10.0 nm, 10.2 nm, and the diffuse transition layer thicknesses are 0.33 nm, 0.75 nm, 1.07 nm, 1.10 nm, respectively. It can be seen that after annealing for 7200 s, the crystalline thickness increase is higher than that of summation of real amorphous and diffuse transition thicknesses. After annealing, the increase of long period mainly comes from the increase of crystalline thickness. This is different from the results given by Carreau, where the long period and crystalline thickness of monolayer PE membrane with shish-kebab structure annealed at 120 °C for 30 min were approximate to those without annealing.41 This may be since the high oriented crystalline shish parts limited the increase of long period during annealing. In our work, no such shish structure can be observed. In addition, the diffuse transition layer thickness is decreased first and enlarged later. At the beginning, the initial transition layer transforms to the ordered crystalline structure, resulting in the decrease of Ld. With annealing, some molecular chains in the amorphous region are included in the transition layer, due to the ordered arrangement movement, leading to the increase of Ld. But it is apparent that at annealing time of 100 s the initial decrease of Ld is approximate to the increase of Lc, whereas at annealing time of 1800 s, the decrease of Ld is not enough to contribute to the increase of Lc. Knowing the average thicknesses of the amorphous and crystalline layers, the linear crystallinity (Xc(SAXS)) of the system was calculated,42
| Xc(SAXS) = Lc/L × 100% | (9) |
 | ||
| Fig. 3 The long period, crystalline thickness, real amorphous thickness and diffuse transition layer thickness (a) and linear crystallinity (b) during annealing at 105 °C. | ||
Upon annealing at 105 °C, the linear crystallinity along the machine direction remains almost constant, as shown in Fig. 3(b).
In situ SAXS results at annealing temperature of 115 °C
Fig. 4 gives the one-dimensional scattering intensity distribution along the machine direction and correlation function during annealing at 115 °C. After annealing, the scattering curve peak moves to lower q value and with increasing annealing time, the scattering intensity increases. After annealing for 7200 s, the intensity is increased from 7 of precursor film to 11, indicating uniform lamellae arrangement. Based on the correlation function in Fig. 4, the long period, the crystalline thickness, real amorphous region thickness and diffuse transition layer thickness were also calculated and shown in Fig. 5. | ||
| Fig. 4 One-dimensional scattering intensity distribution along the machine direction (a) and correlation function (b) during annealing at 115 °C. | ||
 | ||
| Fig. 5 The long period, crystalline thickness, real amorphous thickness, diffuse transition layer thickness (a) and linear crystallinity (b) during annealing at 115 °C. | ||
It can be seen that the long period is increased from 27.5 nm to 30.5 nm for film annealed for 7200 s. After annealing for 100 s, 1800 s, 3600 s and 7200 s, the real amorphous thicknesses are 9.98 nm, 9.88 nm, 9.34 nm, 9.68 nm, and the diffuse transition layer thicknesses are 0.66 nm, 1.11 nm, 1.53 nm, 1.46 nm, respectively; whereas the corresponding crystalline thicknesses are 16.6 nm, 17.6 nm, 17.9 nm and 17.9 nm, respectively. The diffuse layer thicknesses at different annealing time are larger than those at 105 °C. Similar to that at 105 °C, the increase of long period is mainly from the contribution of crystalline thickness increase. Although the annealing temperature is approximate to the maximum crystalline temperature, the long period is increased by only 10.9% after 2 hours annealing, whereas the long period of PE spherulites after annealing for 30 min at 115 °C was increased by 20%.19 This huge difference is mainly since the oriented molecule needs more energy to active and rearrange during annealing. At the same time, the linear crystallinity also does not change much.
In situ SAXS results at annealing temperature of 125 °C
Fig. 6 gives one-dimensional scattering intensity distribution along the machine direction and correlation function during annealing at 125 °C. After annealing, the scattering curve peak moves to lower q value, at the same time, the intensity is increased to more than 12. The correlation function curves move to right with increasing annealing time, indicating the increase of long period. | ||
| Fig. 6 One-dimensional scattering intensity distribution along the machine direction (a) and correlation function (b) during annealing at 125 °C. | ||
Fig. 7 gives the long period, crystalline thickness, real amorphous thickness, diffuse transition layer thickness and linear crystallinity during annealing at 125 °C. Compared with that without annealing, the long period is increased from 27.5 nm to 35.1 nm after annealing for 7200 s. At this annealing temperature, the long period is increased by 27%. This is similar to the result given by Fischer et al.,43 where the long period of PE fibre annealing at 125 °C for 2 hour was increased by 32%. The real amorphous thickness and crystalline thickness are increased from 9.3 nm and 16.1 nm without annealing to 10.4 nm and 21.0 nm, respectively. It is worth noting that the diffuse transition layer thickness is increased from 1.05 nm to 1.84 nm after annealing for 7200 s. Compared with those annealed at 105 °C and 115 °C, the increase of crystalline thickness is pronounced. Although the amorphous thickness is also increased, the long period change is still mainly from the crystalline thickness. The transition layer thickness is slightly decreased at initial annealing stage and then gradually increased. The transformation of transition layer to crystalline phase induces the decrease of transition layer thickness. Meanwhile, at this temperature, the molecule chains within amorphous region show highly ordered rearrangement movement ability. The rearrangement speed is higher than the transformation speed of transition layer to crystalline phase, leading to the gradual increase of diffuse transition layer thickness. But the linear crystallinity still keeps constant during annealing.
 | ||
| Fig. 7 The long period, crystalline thickness, real amorphous thickness, diffuse transition layer thickness (a) and linear crystallinity (b) during annealing at 125 °C. | ||
Comparison of annealing effect at different temperatures
To compare the annealing effect at different temperatures, the long period and crystalline thickness are put together in Fig. 8. Compared with that annealed at 105 °C, at annealing temperature of 115 °C, the long period is increased a little, but it is apparent that annealing at 125 °C induces pronounced long period improvement. Similarly, with increasing annealing temperature, the crystalline thickness is increased, especially at 125 °C. The maximum crystalline temperature and melting peak point of HDPE materials are 114 °C and 130 °C, respectively. Here, the results show that annealing around maximum crystalline temperature does not induce apparent effect. In addition, it is observed that after annealing for 1800 s, the crystalline thickness change appears to be wave-like-increase, decrease and then increase again.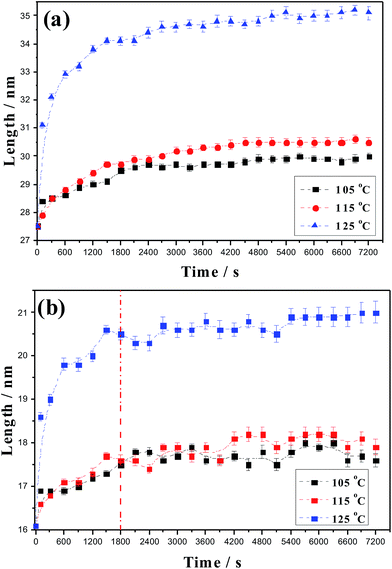 | ||
| Fig. 8 Comparison of long period (a) and crystalline thickness (b) at annealing temperatures of 105 °C, 115 °C and 125 °C. | ||
During annealing, the crystal thickness increase is known as crystal thickening. This thickening process can be regarded as a process of crystal free energy moving to lower state.44 For thin polymer crystals, a thermodynamic force capable of driving the thickening phenomenon arises from the unequal free energies of the fold and lateral surfaces. This process is an irreversible thermodynamic process that can be described by the nonlinear differential equation:20
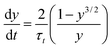 | (10) |
dr ≈ dr(τt) + B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(ta/τt) log(ta/τt)
| (11) |
The long period, crystalline phase thickness, amorphous region thickness and diffuse transition layer thickness as a function of log(t) during annealing are shown in Fig. 9 at three temperatures. The long period is linearly dependent on the logarithm of annealing time. It starts with a horizontal section, sometimes improperly called induction period, at 105 and 115 °C, whereas increases direct linearly at 125 °C. The slope of the long period fit lines using eqn (11) at annealing temperatures of 105, 115 and 125 °C are 1.35, 1.61 and 2.03, respectively. The crystalline phase thickness begins to increase linearly after annealing for 600 s at 105 °C, 100 s at 115 °C and direct linearly increases at 125 °C. The slope of the corresponding fit lines at annealing temperatures of 105 °C, 115 °C, and 125 °C are 0.84, 0.96 and 1.26, respectively. This induction period also exists in the amorphous phase. The linear thickening process begins after 100 s at 105 °C and 115 °C. The slope of the fit lines at annealing temperatures of 105 °C, 115 °C, and 125 °C are 0.42, 0.61 and 0.78, respectively. The amorphous region thickening occurs earlier than crystalline phase at annealing temperature of 105 °C. This may be since the thermal expansion in the amorphous region at this temperature is easier than that of crystalline region. With increasing annealing temperature to 115 °C, the crystallization ability becomes strong, resulting in the fast thickening rate of crystalline region and keeping pace with the increase of amorphous region. For the diffuse transition layer, its increase is later than that of long period. The slope of the fit line for diffusion transition layer versus time curves at annealing temperatures of 105 °C, 115 °C, and 125 °C are 0.51, 0.87 and 0.99, respectively. The transition layer linear increase is slower than that of amorphous and crystalline region, since at initial annealing stage the diffuse transition layer is converted to crystalline layer, resulting in its thickness decrease. These results show strong temperature dependence of the thickening rate within our experimental temperature region. When the annealing temperature is lower than the maximum crystalline temperature, the crystalline and amorphous thickening rate are slow and plenty of time is needed to make the molecules active. Similar phenomenon have been observed during annealing of PE single crystal or the sphaerocrystal.20,21,45
 | ||
| Fig. 9 Change of long period L (a), crystalline phase thickness Lc (b), amorphous phase thickness La calculated from the SAXS data (c) and diffuse transition layer thickness Ld (d) upon annealing time. The straight lines are least-square fit of the data using eqn (11). | ||
To explain the crystal thickness fluctuation at later annealing time in Fig. 8, the TMDSC testing was carried out. Fig. 10 gives the TMDSC curves of films unannealed and annealed at 125 °C for 1800 s, 3600 s and 7200 s, respectively. In the measurement, the obtained total heat flow, approximately equivalent to that from a conventional DSC, can be divided into a (capacity-related) reversible heat flow and a (kinetic) nonreversible heat flow.46 Usually, crystallization and enthalpy relaxation appear only in the nonreversible signals, whereas melting occurs in both reversible and nonreversible signals. For a simultaneous melting and recrystallization process, an endothermic peak in the reversing heat flow and an exothermic peak in the nonreversing heat flow are expected.46,47 For precursor cast film and annealed for 1800 s, only melting curves are seen for the whole melting curve, reversible and non-reversible parts. But after annealing for 3600 s and 7200 s, a weak exothermic peak appears in the non-reversible part. The existence of exotherm peak in the nonreversing heat flow curve indicates the occurrence of melting and recrystallization behavior during annealing at later time. This behavior explains the crystalline thickness oscillation and the small increase of crystalline thickness after annealing from 1800 s to 7200 s in Fig. 8. But during the initial annealing time, this phenomenon is very weak. At annealing temperatures of 105, 115 and 125 °C, the crystalline thicknesses after annealing for 1800 s are increased by 1.4 nm, 1.5 nm and 4.4 nm, respectively, compared with that without annealing. Then, we want to know what induces this increase?
At annealing temperature of 105 °C, the diffuse transition layer thickness after annealing for 100 s is decreased and transformed into crystalline region, leading to the increase of crystalline thickness. But after annealing for 1800 s, the decrease of diffuse transition layer is not enough to induce the increase of crystalline thickness. Therefore, there must be some other phenomena. Barham48 et al. confirmed that the PE crystalline volume expansion was only about 4%. Based on this, the increase of crystalline thickness induced by thermal expansion is about 0.65 nm, smaller than the above crystalline thickness increase induced by annealing.
For polypropylene film with row-nucleated crystalline structure, it has been accepted that secondary crystals from some tie chains in the amorphous region were formed during annealing.10–13 In the work about preparation of HDPE microporous membrane, Lee7 proposed that under high annealing temperature, involving the segments of loose tie chains into the crystallites was probably induced. In addition, it has been found that after annealing, the yield strength in the stress–strain curve was lowered.9 Based on the relationship between the mechanical properties and the fraction of tie chains proposed by Nitta,49 the decrease of yield point mean that some tie chains disappearred during annealing. Where do these tie chains go? They crystallize. Hence, the initial increase of crystalline thickness is mainly from the crystallization of tie chains in the amorphous region. Compared with that without annealing, the crystalline thickness after annealing at 125 °C for 7200 s is increased by 4.9 nm, a little higher than that after annealing for 1800 s. This indicates that during annealing, the contribution of crystallization of tie chains to the increase of crystalline thickness is higher than that from melting and recrystallization behavior.
The above results show that during annealing the linear crystallinity keeps constant. The increase of long period is determined by the crystalline phase thickening, so the linear crystallinity calculated by the SAXS data is kept equalized. Contrary to this, the calculated crystallinity by DSC testing for film annealed at 125 °C for 7200 s is about 65.0%, 6.5% larger than that without annealing. Similar results have been reported in Lee's work.7 In fact, the diffuse transition layer shows higher order than the real amorphous region. The diffuse transition layer thickness is about 10% of the long period after annealing at 125 °C. During the DSC testing, the molecules in diffuse layer also absorb thermal energy. This may be the main reason for the crystallinity difference calculated by SAXS and DSC data.
In situ SAXS results on azimuthal scans at different annealing temperatures
The azimuthal scans of SAXS patterns (a) and full width at half maximum (FWHM) change (b) during annealing are shown in Fig. 11. The azimuthal scans were obtained by integrating in the azimuthal angular range from −45° to 45° as a function of the azimuthal q. The width of SAXS patterns is contributed by the orientation of crystalline lamellae and the lateral size of the lamellae.50 The narrow FWHM corresponds to high oriented crystalline structure51 or long lateral lamellae dimension.50 During annealing, the lamellae extension along the lateral direction is limited. The improved orientation during annealing is the main reason for the width change. Villar52 et al. reported that the FHWM turned small due to higher orientation. Page et al.53 mentioned that the FHWM of the azimuthal peak turned wide with the temperature increasing and they attributed it to the relaxation and disorientation process. From Fig. 11(a), we notice that with increasing annealing time, the intensity increases obviously, indicating the formation of better order lamellae structure during annealing. The SAXS patterns still keep the single peak shape, meaning that a shearing or tilting of the oriented lamellae50,54 does not appear after annealing. The FWHM change during annealing at different temperatures is shown in Fig. 11(b). The FWHM is reduced first and then oscillating changes appear. The decrease of FWHM corresponds to the increase of crystalline orientation degree and the oscillation change is due to the melt-recrystallization process. At 105 °C, the FWHM is reduced from 0.139 nm−1 to 0.130 nm−1 after annealing for 3000 s, and then keeps constant around 0.132, whereas the long period shows wave-like-increase after annealing for 1800 s. But when the annealing temperature is equal or higher than the maximum crystalline temperature, the FWHM oscillating change appears after 1200 s, shorter than the long period oscillating change time of 1800 s. After annealing, the FHWM is reduced from 0.139 nm−1 to 0.120 nm−1 at 115 °C and to 0.126 nm−1 at 125 °C. Contrary to the lamellae dimension change shown in Fig. 8, the annealing temperature near the maximum crystalline temperature results in the apparent increase of crystalline orientation. This difference indicates that the lamellae thickening and orientation degree improving are two separate processes. The higher annealing temperature is beneficial for the lamellae thickening, whereas the annealing temperature around maximum crystalline temperature is useful for the orientation improving. | ||
| Fig. 11 The azimuthal scans of SAXS patterns (a) and full width at half maximum (FWHM) change (b) during annealing. | ||
Relationship between the crystal thickening and annealing temperature
The above results show that lamellae thickening rate exhibits strong dependence on annealing temperature. From Fig. 1, we notice that the 2-lobe patterns have some teardrop structure going into the beamstop and the shape of SAXS patterns shows no change during annealing. This teardrop shape patterns correspond to a stack of parallel lamellae where there is a distribution of crystal lamellae and amorphous thicknesses.55,56 Although the annealing process increases the crystalline and amorphous layer thickness, the polydispersity in the dimension distribution still exists. Fig. 12 gives the structure change during annealing at different temperatures. The thickening process can be divided into two regions. Before 1800 s, the long period is apparently improved and determined by the crystalline phase thickening. Some diffuse transition layer converts to new crystals, and some molecular chains in the amorphous region go into the diffuse transition layer or form some new weak crystals. The obvious increase is observed at 125 °C, higher than the maximum crystalline temperature. With increasing annealing time, the thickening rate turns slow and the wave-like-increase appears. The existence of melting and recrystallization, proved by TMDSC in Fig. 10, after annealing at 125 °C for 3600 and 7200 s, confirms this wave change.Conclusions
The annealing process of HDPE film with row-nucleated crystalline structure at different temperatures was in situ followed using SAXS setup equipped with a temperature-controlling unit. The crystalline phase, amorphous region and diffuse transition layer thicknesses are all increased and show linearly dependent on the logarithm of annealing time. Compared with those at 105 °C and 115 °C, annealing at 125 °C results in apparent increase of crystalline thickness and higher crystalline region thickening rate, but the linear crystallinity does not change much during annealing. The initial crystalline thickness increase is mainly due to the crystallization of molecular rearrangement in diffuse transition layer and amorphous region. At later annealing time, the crystalline thickness versus time curve shows wave-like shape due to the melt and recrystallization process. In addition, the annealing is beneficial for the improvement of crystalline orientation degree. Contrary to the increase of lamellae thickness, the annealing temperature around the maximum crystalline temperature results in apparent increase of the orientation.Acknowledgements
The authors would like to thank National Science Foundation of China under Grant no. 51003017 and the Project of High Level Talents in Higher School of Guangdong Province for financial support. They also want to thank Shenzhen Senior Materials Company, Ltd., for generously supplying raw materials.Notes and references
- S. S. Zhang, J. Power Sources, 2007, 164, 351 CrossRef CAS PubMed.
- F. Sadeghi, Developing of microporous polypropylene by stretching, PhD thesis, Ecole Polytechnique de Montreal, Canada, 2007.
- M. B. Johnson, Investigations of the processing-structure–property relationship of selected semi-crystalline polymers, PhD thesis, Virginia Polytechnic Institute and State University, United States, 2000.
- L. E. Alexander, X-ray Diffraction Methods in Polymer Science, Wiley, New York, 1969 Search PubMed.
- T. H. Yu and G. L. Wilkes, Polymer, 1996, 37, 4675 CrossRef CAS.
- S. H. Tabatabaei, P. J. Carreau and A. Ajji, Polymer, 2009, 50, 4228 CrossRef CAS PubMed.
- S. Y. Lee, S. Y. Park and H. S. Song, J. Appl. Polym. Sci., 2007, 103, 3326 CrossRef CAS.
- S. Y. Lee, S. Y. Park and H. S. Song, Polymer, 2006, 47, 3540 CrossRef CAS PubMed.
- C. B. Chen, C. H. Lei, Q. Cai, H. B. Mo and R. J. Xu, J. Plast. Film Sheet., 2015, 31, 78 CrossRef CAS PubMed.
- C. H. Lei, W. L. Huang, R. J. Xu and Y. Q. Xu, J. Plast. Film Sheeting, 2012, 28, 151 CrossRef CAS PubMed.
- A. Saffar, A. Ajji, P. J. Carreau and M. R. Kamal, Polymer, 2014, 55, 3156 CrossRef CAS PubMed.
- Z. T. Ding, R. Y. Bao, B. Zhao, J. Yan, Z. Y. Liu and M. B. Yang, J. Appl. Polym. Sci., 2013, 130, 1659 CrossRef CAS.
- D. M. Liu, J. Kang, M. Xiang and Y. Cao, J. Polym. Res., 2013, 20, 126 CrossRef PubMed.
- Q. Cai, R. J. Xu, S. Q. Wu, C. B. Chen, H. B. Mo, C. H. Lei, L. B. Li and Z. H. Li, Polym. Int., 2015, 64, 446 CrossRef.
- A. Peterlin, J. Polym. Sci., Polym. Symp., 1965, 9, 61 CrossRef.
- A. Peterlin, Makromol. Chem., 1964, 74, 107 CrossRef CAS.
- A. Peterlin, J. Polym. Sci., Polym. Lett., 1963, 1, 279 CrossRef CAS.
- A. Peterlin, Polymer, 1965, 6, 25 CrossRef CAS.
- W. O. Statton and P. H. Geil, J. Appl. Polym. Sci., 1960, 3, 357 CrossRef CAS.
- I. C. Sanchez, J. P. Colson and R. K. Egy, J. Appl. Phys., 1973, 44, 4332 CrossRef CAS PubMed.
- I. C. Sanchez, A. Peterlin, R. K. Egy and F. L. McCrackin, J. Appl. Phys., 1974, 45, 4216 CrossRef CAS PubMed.
- L. Wang, Q. P. Zhang, J. H. Wang, B. Yang, M. B. Yang and J. M. Feng, Polym. Int., 2014, 63, 296 CrossRef CAS.
- S. Yilmaz, T. Yilmaz and A. A. Arici, J. Mater. Sci., 2011, 46, 1758 CrossRef CAS.
- S. Song, J. Feng and P. Wu, J. Polym. Sci., Polym. Lett., 2011, 49, 1347 CrossRef CAS.
- B. R. de Gáscue, J. L. Prin, G. Hernández, E. M. Vallés, A. T. Lorenzo and A. J. Müller, J. Therm. Anal. Calorim., 2011, 103, 669 CrossRef.
- Z. Li, Z. Wu, G. Mo, X. Xing and P. Liu, Instrum. Sci. Technol., 2014, 42, 128 CrossRef CAS.
- X. Sun, J. Liu, I. Takahashi and S. Yan, RSC Adv., 2014, 4, 39101 RSC.
- J. Dong, C. Yin, J. Lin, D. Zhang and Q. Zhang, RSC Adv., 2014, 4, 44666 RSC.
- Z. Wei, R. Lun, X. Lou, F. Tian, J. Lin, X. Li, J. Yu and F. Li, RSC Adv., 2014, 4, 64625 RSC.
- O. Glatter and O. Kratky, Small-Angle X-ray Scattering, Academic Press, London, UK, 1982 Search PubMed.
- B. Crist and N. Morosoff, J. Polym. Sci., Polym. Lett., 1973, 11, 1023 CAS.
- G. R. Strobl and M. Schneider, J. Polym. Sci., Polym. Lett., 1985, 23, 2517 CrossRef.
- C. G. Vonk, J. Appl. Crystallogr., 1973, 6, 81 CrossRef CAS.
- C. G. Vonk and A. P. Pijpers, J. Polym. Sci., Polym. Lett., 1985, 23, 2517 CrossRef CAS.
- G. R. Strobl and M. Schneider, J. Polym. Sci., Polym. Lett., 1980, 18, 1343 CrossRef CAS.
- G. R. Strobl, M. Schneider and I. G. Voigt-Martin, J. Polym. Sci., Polym. Lett., 1980, 18, 1361 CrossRef CAS.
- W. Ruland, J. Appl. Crystallogr., 1971, 4, 70 CrossRef.
- W. Ruland, Colloid Polym. Sci., 1977, 255, 417 CAS.
- M. H. Kim, J. Appl. Crystallogr., 2004, 37, 643 CrossRef CAS.
- D. L. Chinaglia, R. Gregório and D. R. Vollet, J. Appl. Polym. Sci., 2012, 125, 527 CrossRef CAS.
- S. H. Tabatabaei, P. J. Carreau and A. Ajji, J. Membr. Sci., 2009, 345, 148 CrossRef CAS PubMed.
- B. Heck, T. Hugel, M. Iijima, E. Sadiku and G. Strobl, New J. Phys., 1999, 1, 17 CrossRef.
- E. W. Fischer and G. F. Schmidt, Angew. Chem., Int. Ed., 1962, 1, 488 CrossRef.
- C. Hedesiu, D. E. Demco, R. Kleppinger, G. V. Poel, W. Gijsbers, B. Blümich and V. M. Litvinov, Macromolecules, 2007, 40, 3977 CrossRef CAS.
- I. Okazaki and B. Wunderlich, J. Polym. Sci., Polym. Lett., 1996, 34, 2941 CrossRef CAS.
- Y. Lee and R. S. Porter, Macromolecules, 1987, 20, 1336 CrossRef CAS.
- Y. Lee, R. S. Porter and J. S. Lin, Macromolecules, 1989, 22, 1756 CrossRef CAS.
- P. J. Barham and A. Keller, J. Mater. Sci., 1977, 12, 2141 CrossRef CAS.
- K. H. Nitta and M. Takayanagi, J. Polym. Sci., Polym. Lett., 2000, 38, 1037 CrossRef CAS.
- Y. F. Men, J. Rieger, P. Lindner, H. F. Enderle, D. Lilge, M. O. Kristen, S. Mihan and S. Jiang, J. Phys. Chem. B, 2005, 109, 16650 CrossRef CAS PubMed.
- A. Prasada, R. Shroff, S. Rane and G. Beaucag, Polymer, 2001, 42, 3103 CrossRef.
- M. A. Villar, D. R. Rueda, F. Ania and E. L. Thomas, Polymer, 2002, 43, 5139 CrossRef CAS.
- A. K. Page, A. F. Landis, K. A. Phillips and B. R. Moore, Macromolecules, 2006, 39, 3939 CrossRef.
- N. S. Murthy, C. Bednarczyk, R. A. F. Moore and D. T. Grubb, J. Polym. Sci., Part B: Polym. Phys., 1996, 34, 821 CrossRef CAS.
- E. L. Heeley, T. Gough, D. J. Hughes, W. Bras, J. Rieger and A. J. Ryan, Polymer, 2013, 54, 6580 CrossRef CAS PubMed.
- J. K. Keum, R. H. Somani, F. Zuo, C. Burger, I. Sics, B. S. Hsiao, H. Y. Chen, R. Kolb and C. T. Lue, Macromolecules, 2005, 38, 5128 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2015 |



