Excited-state deactivation mechanisms of protonated and neutral phenylalanine: a theoretical study†
Abstract
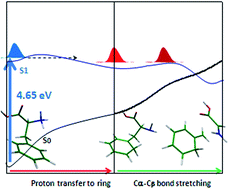
The potential energy (PE) profiles of neutral and protonated phenylalanine, as the simplest aromatic amino acid, at different electronic states have been investigated extensively using RI-MP2 and RI-CC2 methods. The PE profiles have been determined, considering the Cα–Cβ and Cα–C(COOH) bond stretching following proton transfer to the aromatic ring and CO group, respectively, as well as the hydrogen detachment reaction coordinate. The calculated results reveal that a low-barrier proton transfer process from ammonia to the aromatic chromophore, leading the excited system to Cα–Cβ bond cleavage, plays the most prominent role in the deactivation mechanism of excited PheH+ at the origin of the S1–S0 electronic transition. On the contrary, for excited neutral phenylalanine at the band origin of the S1–S0 transition, a large barrier in the S1 profile along the Cα–Cβ bond-stretching hinders the excited system from approaching the dissociative part of PE curve. This barrier may explain the large lifetime of the S1 excited phenylalanine (nanosecond range), while a low barrier in the S1 PE profile of the protonated species along the PT process explains the short-range lifetime of the protonated species (in the picosecond range).


 Please wait while we load your content...
Please wait while we load your content...