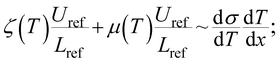Thermally enhanced self-propelled droplet motion on gradient surfaces†
Monojit Chakrabortya,
Udita Uday Ghosha,
Suman Chakrabortyb and
Sunando DasGupta*a
aDepartment of Chemical Engineering, Indian Institute of Technology Kharagpur, India. E-mail: sunando@che.iitkgp.ernet.in; sunando.dasgupta@gmail.com; Tel: +91-3222-283922
bDepartment of Mechanical Engineering, Indian Institute of Technology Kharagpur, India
First published on 1st May 2015
Abstract
Significant enhancements in the instantaneous speed of a water droplet on a silicon surface with a chemically induced hydrophilicity gradient are observed with moderate increases in substrate temperature. The instantaneous droplet velocities and the contact angles are measured by a frame by frame analysis of the droplet motion using a goniometer with a high speed camera. A force balance based model captures the underlying experimental trends in a precise quantitative sense. The relevant forces are the chemically induced surface tension gradient inspired driving force and the resistive forces namely, the three-phase contact line, hydrodynamic and the drag force. The variation in the values of the coefficient of contact line friction and its effect on the overall droplet transport has been evaluated. This study points to the enhanced cooling potential of speciality surfaces where the dissipated heat may be utilized as a natural advantage for faster movement of droplets towards the hot spot.
1. Introduction
Superior control and enhancement of surface energy gradient induced flow has been the subject of intense interest1,2 for its applications in microfluidic device design and operation as well as in a number of emerging technologies such as coating, printing and photolithography. A spatial non-homogeneity in surface tension may be imparted to a surface by adsorption and desorption of surface active molecules,3 chemical reactions,4 or chemical patterns.5,6 The subsequent changes in contact angles lead to non-mechanical liquid control7–9 and can be further enhanced by additional means to ensure faster liquid movement.10,11Droplet motion can be induced on a surface by applying optical, thermal, acoustic or electrical energy.12 In optofluidics, a tiny drop of fluid can be set in motion by controlling the optical intensity and direction.13 This optical augmentation in droplet manipulation leads to significant development in lab on chip devices. Recently developed wettability patterning techniques offer selective wettability conversion from superhydrophobic to superhydrophilic states on non-planar substrates and have been used to perform complex droplet operations.14 Similarly, surface acoustic waves have been used for droplet manipulation in microfluidic channels.15 Electrical energy has also been employed extensively as a source of electromechanical actuation of droplet on digital microfluidic platform.16 However, these methods require external energy to trigger and sustain droplet movement. It is in this scenario that gradient surfaces emerge as an alternative to obtain sustainable micro-droplet movement by modifying the substrate properties and thereby eliminating the need of an energy source. Gradient surfaces can be divided into two major classes: morphological gradients and chemical gradients. Morphological gradients comprise of gradient due to varying surface roughness and fabricated micro-structures, whereas chemical gradient surfaces consists of gradients produced by modification in surface topography by chemical treatment.12 Laser etching has also been used to create topography based surface tension gradients on metallic surfaces.17 Radial wettability gradient patterns comprising of a hydrophobic perfluorodecyltrichlorosilane (PFDTS) circle at the center and surrounded by stripes of alternating wettabilities, i.e., hydrophilic and hydrophobic have now been achieved at the experimental scale.18
A gradual change in the wetting property of liquid droplets over a surface produced by varying deposition of specific chemicals is capable of inducing droplet movement. Brochard1 theoretically postulated droplet movement induced by chemical and thermal gradients on the basis of change in surface energies. She considered droplet movement under the condition of partial wetting for different droplet configurations of ridge or strip and spherical cap. This theory was extended for the condition of complete wetting. Brochard suggested that droplet movement induced by thermal gradient is a consequence of superposition of Marangoni flow on the drift induced by the solid surface. Chaudhury et al.3 were the first to experimentally demonstrate droplet movement on a surface possessing wettability gradient (change in contact angle from 97° to 25°) over a distance of 10 mm. This motion was also shown to be sustainable with an average velocity of 1–2 mm s−1 on an inclined plane (15°). Suda and Yamada19 measured the driving force acting on the droplet using a micro-needle. They found that only hydrodynamic friction was not sufficient to counteract the experimentally measured driving force and proposed that the droplet should be considered as a set of solid-like domains instead of hydrodynamic continuum and the solid-like friction between these domains were to account for the anomaly in the driving force. Subramanian et al.20 put forth two analytical solutions for the driving force and quasi-steady state velocity of droplet motion over a wettability gradient. The first approach approximated the drop as a collection of wedges and for small contact angles, the predicted velocity was found to be twice the speed given by Brochard.1 The second approach was based on the lubrication approximation, where the driving force was equated with the hydrodynamic resistance acting over the entire droplet instead of Brochard's method of local balance of normal forces on a differential element of the contact line. These models were partially validated by quantifying the change in instantaneous droplet velocity with position along the wettability gradient. This was carried out for different droplet volumes and the variation in velocity was suggested to be a result of varying driving force as well as hydrodynamic resistance along the gradient.21 Zhao and Beysens22 studied the effect of wettability gradient (surface heterogeneity) on the process of condensation. Three distinct regimes were outlined based on the difference in the morphology of condensation patterns of spherical droplets and quasi-films on the hydrophobic and hydrophilic side respectively, whereas the crossover region was represented by islands of non-spherical droplets. This difference in patterns was attributed to the microscopic manifestation of the surface heterogeneity in the form of contact line pinning.
Enhancement in droplet velocity when it moves over a wettability gradient surface can be brought about by combining additional surface gradients arising out of supplementary forces. This was first demonstrated by the research group of Chaudhury, where they showed that for condensation on a hydrophilicity gradient surface, the velocities of the droplets thus formed can be hundred to thousand times more as compared to typical Marangoni flows.11 This may turn out to be of prime importance in enhancing the heat transfer rate in heat pipes and exchangers. The same group also showed that droplet movement over wettability gradient surface may be augmented by subjecting it to mechanical vibrations in the form of square waves.23 This resulted in enhanced droplet speed of 5–10 mm s−1. However, it was found that the addition of body force to the wetting force induced by vibration was more effective for surfaces having low hysteresis. This was followed up by the observation that amplified droplet speeds could be obtained, if the frequency of vibration to which the droplet was subjected to coincides with its first and second spherical harmonics. Chaudhury's group proposed that this phenomenon was a result of droplet shape fluctuation, induced by resonant frequencies, leading to successive pinning and depinning of the contact line from its metastable states.24
Droplet motion can also be initiated by the application of thermal gradient. Brzoska et al.25 showed that droplet movement was feasible on hydrophobic surfaces by applying thermal gradients. However, this movement was found to occur only above a certain droplet radius termed as critical radius. The critical radius was found to be a strong function of the contact angle hysteresis. The droplet impact kinetics was also found to be directly linked with the shape attained by the droplet when it comes in contact with chemically patterned stripes.26 Ford and Nadim27 theoretically derived expressions for the velocity and pressure fields within the droplet under imposed thermal gradients using lubrication approximation and also incorporated a slip coefficient to relieve the stress singularities at the contact line. Pratap et al.28 investigated the effect of droplet size and imposed thermal gradient on droplet velocity by observing the movement of decane droplets on PDMS coated glass surfaces. However, they found that droplet movement under applied thermal gradient to be independent of the critical footprint radius, unlike the prediction of Brzoska et al.25 Mettu and Chaudhury29 showed that droplet speeds under the influence of thermal gradient can be further increased by subjecting it to mechanical vibrations. The effect of amplitude and vibration frequency on the reduction of contact angle hysteresis had been outlined in detail. In accordance with the previous observations, it was found that droplet velocity exhibited maxima at resonant frequencies.
It is to be noted that application of thermal gradient to the scale that affects the droplet velocity is difficult to achieve and requires involved fabrication.
In the present work, significant enhancements in droplet motion are reported on a wettability gradient surface at elevated temperatures. The rise in temperature is achieved by subjecting the surface to constant heat fluxes. The instantaneous velocities and contact angles are measured and the enhancements in the velocities as a function of the substrate temperature are quantified. A theoretical model based on a force balance approach has been developed to take into account the forces present. The model is used to corroborate the experimental data and to examine the behaviour of the forces at elevated temperatures. The study addresses some of the fundamental scientific issues related to the reduction of contact line friction forces with increase in temperatures, resulting in amplification of self-propelled droplet motion.
2. Experimental methods
The experiments consist of characterizing the movement of a de-ionized water droplet on a substrate with chemically imparted wettability gradient, measuring the instantaneous contact angles using a goniometer with a data acquisition system to record and analyze the movement of the droplet. The videos of the droplet movement were captured (see ESI1 and 2† for droplet movement at 25 °C and 65.7 °C) using DropImage Advanced software integrated with the goniometer.2.1 Preparation and characterization of wettability gradient
Silicon wafers of 2 inch diameter, single side polished with an orientation of 〈100〉 ±0.5° having resistivity of 0.01–0.02 Ohm cm (grade: Prime-CZ, thickness: 275 ± 25 μm) were used as the substrate, due to well standardized cleaning and handling techniques and because of its wide use as a substrate in the electronics industry. The wafers were initially dipped in a freshly prepared piranha solution (70% sulphuric acid–30% aqueous solution of hydrogen peroxide) for 30 minutes. It was then thoroughly rinsed with DI water followed by drying in an oven at 95 °C for 20 minutes. To remove the residual organic contaminants on the substrate, a plasma cleaning technique utilizing oxygen plasma (RF discharge as plasma generation source) was used for about 5 minutes. The exposure to plasma served two purposes – cleaning as well as hydroxylation (addition of –OH groups), which in turn increased the wettability of the surface.The cleaned and oxidized substrate was placed horizontally at about 2 mm above the open tip of an inverted micropipette (sealed from below) containing 50 μl of 50% decyltrichlorosilane (DTS, Cl3Si(CH2)9CH3) solution in toluene (see Section 1 of ESI3†). The tip of the micropipette was positioned at the centre of the Si wafer. The diffusing DTS deposits on the substrate and results in a natural gradient of wettability with gradually decreasing DTS content from the centre of the substrate. The substrate as a result will have increasing hydrophilicity with distance from the centre. The entire operation was performed in a laminar flow clean hood for about 3–4 hours at room temperature (25 °C). DTS diffused through the vapour phase and reacted with the silicon surface. The steps involved are hydrolysis leading to the formation of silanol groups, followed by hydrogen bonding with the OH groups of the substrate and finally a covalent linkage with the substrate along with the condensation of water molecules. This covalent linkage exposed alkyl group to the atmosphere resulting in increased hydrophobicity. The steepness of the gradient was found to be a function of time of exposure, concentration of DTS in the solution, and the temperature at which the substrate was exposed to the diffusing front of DTS and were optimized to obtain the desired result. Atomic force microscope (AFM) (AGILENT Nanonics Model no. 5100) with a silicon cantilever was used in the intermittent contact imaging mode (tapping) to characterize the wettability gradient surface. Wafers were scanned prior to silanization (bare silicon wafer) as well as post silanization. RMS roughness30 of the silicon wafer surface is defined as the standard deviation of the elevation and was used to characterize the deposition of DTS on the surface. The RMS roughness of the bare silicon wafer (calculated using image processing software Pico View attached with the AFM) was found to be 0.987 nm, whereas silanized wafer gave an RMS roughness of 25.6 nm indicating silane deposition on the surface. It is pertinent to note that even though the substrate has a nanoscale surface roughness, the friction induced by such nano-rough surfaces may not be sufficient enough to mask the friction acting over the molecular scale.31 The effect of temperature elevation on the nature of the silane deposit over the substrate was checked as well. The heated silanized wafer gave an RMS roughness of 26.4 nm which is of the same order as it was before the heat treatment. This confirms that there were no morphological changes of the substrate at elevated temperatures.
A 2.5 μl droplet of DI water was placed at the centre of the prepared gradient surface. A schematic of the experimental setup is shown in Fig. 1. The droplet immediately started to move along the gradient from the hydrophobic centre towards the hydrophilic edge. Movement of the droplet was recorded using the image analyzing software attached with the goniometer. The static contact angle distribution along the path of the droplet (2.5 μl) movement was difficult to measure as the droplets move instantaneously due to the presence of wettability gradients. An attempt was made using droplets of lesser volume but that has led to additional difficulties and uncertainties. Therefore the front and the rear contact angles were measured using a goniometer for each frame of the extracted images (from the captured droplet movement video) and presented in Fig. 2.
 | ||
| Fig. 2 Spatial Variation of contact angle at 25 °C. ±1–3% error is associated with each experimental value. | ||
2.2 Application of heat
A DC dual power supply source (Testronix 93C) was used to supply constant heat to the substrate through a strip heater attached below the substrate. Images of the temperature distribution on the substrate at each heat load were captured using an Infra-Red (IR) thermal imaging camera (FLIR SC5000). The mean and maximum temperatures at the hydrophobic center and its surrounding were obtained from the software (Altair: version 5.80.016) attached with Infra-Red (IR) camera (with a temperature sensitivity of 0.020 °C).2.3 Data acquisition and determination of droplet velocities
Droplet motion was captured at 70 frames per second using DropImageAdvanced software attached with the goniometer (Ramehart, Germany). Images at different time intervals were extracted from the captured videos. The motion of the center of the droplet was tracked from one frame to the next using Image-Pro Plus software in a sequential fashion.The experiments were repeated a number of times (at least three) and the average of these data sets were used for the evaluation of droplet instantaneous velocity and forces acting on the droplet. The initial displacement of the droplet occurred very fast as the droplet covered about ∼2 mm in the first ∼0.5 s. It slowed considerably in subsequent stages; traversing only about 0.8 mm in 1.75 s (as shown in Fig. 3) at 25 °C. The hydrophobic centre is the epicentre of minimal surface energy and this surface energy increases radially from the centre towards the periphery with an increase in hydrophilicity. Thus, the droplet traces a path of varying wetting property and comes to halt when this variance is no longer sufficient to sustain the movement of the droplet.
 | ||
| Fig. 3 Distance traversed by the droplet as a function of time at 25 °C. ±1–3% error is associated with each experimental value. | ||
3. Theoretical formulation
The driving forces for the droplet movement can be equated to the resistive forces acting on the drop, to evaluate the instantaneous velocity using quasi-steady approximation. The relevant forces are the surface tension gradient inspired driving force (Fdriving) and the resistive forces namely, the three-phase contact line (Fcl), the hydrodynamic (Fh) and the drag (Fd) force. The validity of the quasi-steady approximation has been established before,20 for similar conditions. The approximation is further validated by comparing the transient time scale (∼6.9 × 10−3 s) and the viscous relaxation time scale (∼2.24 s).20 It is also important to mention here that in the present work, the effect of gravity and inertial forces are neglected as the capillary number, Bond number and Weber number for a droplet of volume 2.5 μl (r = 1.06 mm) are found to be in the range of 1.85 × 10−5 to 4.94 × 10−4; 0.153; and 0.13 to 0.64, respectively. Therefore,| Fdriving = Fh + Fdrag + Fcl | (1) |
The difference in the front (advancing) and rear (receding) and contact angles (a manifestation of the change in surface energies) is quantified at each time instant during the movement of the droplet and is used to evaluate the driving force at that location. The expression for the driving force is20
| Fdriving = 2R(x)γg(θ) | (2) |
here R(x) is the radius of the footprint of the drop, obtained from the extracted images of the droplet (using DropImageAdvanced software attached with the goniometer). The subscripts f and r correspond to “front” and “rear” droplet contact angles respectively and γ is the liquid–gas interfacial tension.
Subramanian et al.20 have put forth an analytical expression based on the wedge approximation in which the Stokes flow condition analysis by Cox32 is used to predict the hydrodynamic force exerted by solid surface (silicon wafer) on the liquid drop as,
| Fh = (8μU(x)R(x)f(θ, ε)) | (3) |
and ε = Ls/R, where, μ is the viscosity of water and Ls is the slip length.20 Here U(x) is the instantaneous velocity of the drop; R is the radius of the drop's footprint. Coordinate axes are scaled by R to obtain the dimensionless co-ordinates (X, Y) and θ is the dynamic contact angle of the drop. Reported molecular dynamics (MD) simulations20 depicting similar physical paradigm as portrayed by the conditions encountered in this study indicated slip length values in the range of 0.5 nm. However, we have observed that the alteration of slip length even by one order has negligible effect on the overall estimation of instantaneous drop velocity.
The droplet will experience a drag force if it is encapsulated by a filler medium. Under such conditions the filler media (in this case, air) forms a barrier between the drop and the surface, thereby acting as an opposing force. This drag force can be expressed mathematically as33
 | (4) |
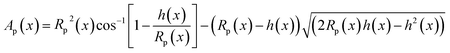 | (5) |
To calculate Rp(x), the droplet has been assumed to be a spherical cap. The volume of the droplet may be expressed as function of the droplet radius RP(x), and the height h(x) as,
 | (6) |
The values of the height of the drop ‘h(x)’ are obtained from the extracted images (using DropImage Advanced software) of the droplet for the known droplet volume ‘V’. The values of RP(x) are evaluated using the above equation.
Dynamic wetting occurs as the droplet moves along the migration path starting from the hydrophobic centre towards the lesser hydrophobic region (in the direction of increasing hydrophilicity). This dynamic wetting can be visualised as the displacement of the three phase contact line from one location to another. Such instantaneous displacement or jump of the contact line leads to dissipation that involves loss of energy at the molecular level.35 However, this jump is essential for the advancement of the contact line. Molecular kinetic theory (MKT) has been used to express the functionality of the three-phase contact line force and friction,33 generated due to the advancement of the three phase contact line.
| Fcl = 2P(x)ζU(x) | (7) |
Substituting eqn (2)–(4) and (7) into eqn (1), a quadratic equation in U(x) is obtained as,
 | (8) |
Solution to eqn (8) provides the expression of U(x) as,
 | (9) |
4. Results and discussions
A closer examination of eqn (9) reveals that U(x), the instantaneous velocity, is a function of geometric parameters, physical property, contact angles and the coefficient of the wetting line friction, ζ. Contact line friction stems from the fact that the origin of three phase contact line force is fundamentally molecular in nature, and the force signifies the loss in energy associated with the displacement of the three phase contact line from one location to another. This force,38 in its analytically tractable form, may be parameterized in terms of ζ. There are very few reports on the values of ζ in the literature, with ranges from 0.01 for water on polyethelene terephthalate tape to a value of 3580 for silicone oil on glass.39 The value of ζ is obtained herein by minimizing the root mean square error between the theoretically predicted velocities with the experimental values and is found to be 0.15 Pa s at 25 °C which is in the expected range40 as reported in a similar study. Furthermore, it is worth recognizing that the mobility law given by eqn (9) is not universal, but essentially describes a particular situation in which there occurs a combination of droplet spreading due to dynamic wetting, as well as dynamic wetting superimposed on physical ‘movement’ of the droplet. Thus invoking standard expressions of MKT may not present a complete description of the phenomena (discussed in detail in Section 2 of ESI3†). This underscores the necessity of considering a balance between the various driving and opposing forces along with the ‘local contact line dissipation’.The spatial variations of the driving and the three resistive forces are plotted in Fig. 4. It can be clearly seen that the driving force is large in the initial stages of the movement, reaching a maxima and decreasing thereafter, mirroring the trend in the experimentally measured droplet velocity. The non-uniform driving force (arising due to the wettability gradient) is responsible for the observed trend of velocity profiles in the experiments. This non-uniformity in driving force is a manifestation of the varying dynamic contact angle differences (between the front and the back end of the droplet) and droplet footprint radius. However, the interesting outcome of the force calculation is the predominance of the three phase contact line force over the other two resistive forces, namely the hydrodynamic and the drag forces.
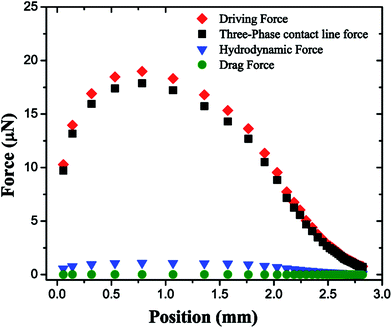 | ||
| Fig. 4 Forces acting on the droplet of Fig. 3. | ||
The theoretically predicted values from eqn (9) and the experimentally measured values of the instantaneous velocities are presented in Fig. 5. It is to be noted that using the contact line friction coefficient as the only fitting parameter, the physics of the process is satisfactorily described and the trends in the values of the evaluated parameter are consistent with a study involving MD simulation.41
 | ||
| Fig. 5 Comparison of the predicted and experimental instantaneous velocity profiles (substrate temperature at 25 °C). | ||
4.1 Effect of elevated temperature
In an effort to study the effect of increases in temperature elevation, a heater of size 600 mm2 (20 mm × 30 mm) (while the droplet area varies from 4.828 mm2 to 10.094 mm2) is attached below the substrate with the hydrophilicity gradient. The droplet movement over a wettability gradient surface with no heat load (substrate temperature at 25 °C) is taken to be the base case. The experiments are carried out for four constant heat loads of 0.25 W, 0.53 W, 0.9 W and 1.65 W resulting in progressive increase in substrate temperature. It is to be noted that the heat loads mentioned here are only representative system specific values and are not used in any subsequent calculations. The variation in the droplet velocity and other parameters are examined as functions of temperatures only. Thermal images are taken at each heat load and a line profile of temperature (see Section 3 of ESI3†) is used to obtain the pixel wise (1 pixel = 0.625 mm) temperature distribution including the maximum, minimum and mean temperatures along the length of the gradient track and are tabulated in Table 1. The temperature distribution is fitted with a 4th degree polynomial (with r2 = 0.98) and dT/dx is calculated at every pixel. The highest value of the gradient is found to be in the range of 0.08–0.20 °C mm−1.| Applied heat load (W) | Droplet track temperature (maximum) (°C) | Droplet track temperature (mean) (°C) |
|---|---|---|
| 0 | 25 | 25 |
| 0.25 | 33 | 32.1 |
| 0.53 | 37.5 | 36.5 |
| 0.9 | 47.9 | 46.8 |
| 1.4 | 52.6 | 50.8 |
| 1.65 | 67.2 | 65.7 |
Significant increases in the droplet velocities with increase in droplet track mean temperature are observed, as depicted in Fig. 6; for example the peak instantaneous velocities increase from 6.55 mm s−1 at 25 °C to 40.18 mm s−1 at 65.7 °C. Variation of droplet footprint radius and height, with temperature are shown in Fig. 7. The experimentally evaluated difference between the cosines of the front (advancing) and the rear (receding) end contact angles of the droplet more than doubled (as compared to the room temperature situation) when the droplet track mean temperature is increased to 65.7 °C as shown in Fig. 8, (where the differences are plotted against dimensionless droplet travel distance). However, the experiments are sensitive to the number of times a specific substrate is used and it is reported that the microscopic residues left behind by a moving drop can interfere with that of subsequent drops on the same path.21 This approach of ensuring that the droplets travel on separate unused migration paths on the strip has also been reported in the literature.21 This needs to be emphasized that the reproducibility of the droplet velocity is reasonably good when they travel on such unused paths. To obtain a reference scale we have non-dimensionalised the distance with respect to the distance traversed by the droplet before coming to rest.42
 | ||
| Fig. 7 Spatial Variation of drop (a) footprint radius and (b) height. ±1–3% error is associated with each experimental value. | ||
An increase in instantaneous velocity with dimensionless distance on increasing the droplet track mean temperature is shown in Fig. 9. The combined effects of wettability and rise in temperature are manifested by a concomitant increase in the instantaneous velocity. The time scale of droplet evaporation is significantly higher (few minutes) for a volume ∼2.5 μl at the highest temperature used herein; compared to droplet traversing time (less than one second at elevated temperature). Similar values for droplet evaporation time were reported earlier.43,44 In addition, the droplet volumes are measured (at the start and at the end of the droplet movement, using a goniometer) for each operating temperature and no appreciable loss in droplet volume is observed. The three phase contact line force is found to be the major retarding force (Fig. 4) for movement of droplets on wettability gradient surfaces. The significant aspect of droplet movement influenced by elevated temperature is a decrease in the major opposing force (three phase contact line force) resulting in enhancement of the droplet mobility. The origin of three phase contact line force, as discussed earlier, is molecular in nature and signified the reduction in energy associated with the displacement of the three phase contact line from one location to another. This force depends greatly on the coefficient of contact line friction,33,38 as quantified by the parameter ζ. The values of the parameter ζ, at elevated temperatures, are calculated using the same approach as discussed earlier, and are presented in Table 2.
 | ||
| Fig. 9 Effect of temperature elevation on instantaneous droplet velocity. (A, C and E are experimental observation and B, D and F are the velocities calculated using eqn (9) at 25 °C, 36.48 °C and 65.72 °C respectively). ±1–3% error is associated with each experimental value. To enhance readability, results of only three temperatures are presented here. | ||
| Droplet track temperature (mean) (°C) | Coefficient of contact line friction ζ (Pa s) |
|---|---|
| 25 | 0.15 |
| 32.1 | 0.115 |
| 36.5 | 0.085 |
| 46.8 | 0.0625 |
| 50.8 | 0.0425 |
| 65.7 | 0.0325 |
The results show a significant decrease in ζ with increase in droplet track temperature. It is evident that available additional energy alters the coefficient of the contact line friction appreciably. Taking into account the fact the that the coefficient of contact line friction originates from the contact line dissipation35,37,38,40,45,46 occurring at the molecular level, it can be postulated that increase in temperature increases the kinetic energy of the molecules at the three phase contact line region. The movement of the droplet always occurs in the direction of increasing hydrophilicity, as one end of the droplet experiences a more hydrophilic region relative to the other end. The effect of elevated temperature and the associated increase in the kinetic energy of the molecules near the contact line essentially augments this hydrophilicity induced, direction specific droplet motion. Thereby the elevated temperatures influence two aspects of the droplet movement. It leads to a larger wettability variation from the front to the rear of the drop due to larger spreading on the surface (Fig. 8) and reduces the contact line friction, as shown in Table 2 and is in tune with the observations of the MD simulations.41
To verify the effect of temperature on droplet mobility on substrates with uniform wettability, different set of experiments are performed. Substrates of uniform hydrophibicity is prepared by spin-coating (3000 rpm for 30 seconds) a thin layer of Teflon on cleaned silicon wafer and by curing at 110 °C for 10 minutes, followed by 20 minutes at 175 °C.44 This rendered the substrate surface hydrophobic with a mean equilibrium contact angle of ∼117° for DI water droplets. The substrate is placed on the automated tilting base of the goniometer stage and inclined at an angle of 21.1°, allowing droplet movement under the influence of gravity. The droplet movements are captured and analyzed in the same manner as described before for three different mean substrate temperatures of 25 °C, 47.1 °C and 68.4 °C. Substrate mean temperatures are measured using IR camera and using thermal imaging technique as discussed earlier. Appreciable increases in the average velocities of the droplets are observed – from 8.5 mm s−1 at 25 °C, to 22.2 mm s−1 at 47.1 °C and 51.8 mm s−1 at 68.4 °C. The results further highlight the fact that droplet mobility gets enhanced with temperature even on a uniform wettability surface.
The thermal gradient found in the present study is significantly less than that required to trigger thermocapillary actuation as reported in a number of studies.25,29 In their experiments, Mettu and Chaudhury29 did not observe any movement of the liquid (DI water) drops on a substrate having a linear variation of temperature less than 0.8 °C mm−1; the value of which is significantly higher than the gradient created (ranges from 0.08–0.20 °C mm−1) in our case, even at the highest elevated temperature reported in the experiments. They resorted to programmed vibration of the substrate to achieve droplet movement with maximum velocities around 1.2 mm s−1, which is lower than the velocities obtained in the present case (around 40 mm s−1). Similar observations were also reported28,47 where droplet movements were initiated by imposing a thermal gradient of more than 2 °C mm−1.
Thermocapillary or Marangoni flow occurs when the available surface tension gradient is sufficient enough to counter the pinning and viscous force acting on the droplet. An order of magnitude analysis has been carried out to evaluate the effect of surface tension gradient on the major opposing forces, namely the pinning and the wall shear forces, so as to establish the velocity scale (Uref) governed by Marangoni effects. The effect of air-liquid drag force has been excluded from the analysis as it has negligible influence over the present phenomena. In symbolic notations, the order of magnitude analysis reveals
 | (10) |
It can therefore be interpreted that thermal gradients present in the current study are not sufficient for thermocapillary migration of the drop. However, in conjunction with wettability gradient, it can give rise to significant droplet movement and can have important potentials for practical applications.
The roughness of experimental surfaces was measured by AFM and was found to be in the nanometre scale. It has been clearly mentioned in the literature31 that the dynamic contact angle behaviour does not alter from smooth to nano-rough surfaces, considering the temporal regimes of the dynamic experiments. It is further important to recognize that the molecular kinetic theory (MKT), as adopted herein for characterizing contact angle friction, is capable of providing an effective description of the contact line motion even in presence of surface heterogeneities.9,48,49 We have also conducted additional experiments to examine the effects of the variation of chemical coating, heating power and droplet volume on droplet motion (see Section 4 of ESI3†).
5. Conclusion
Enhancements in the rate of transport of a droplet with increase in substrate temperatures on a silicon substrate under wettability gradient conditions were observed and accurately measured. The peak instantaneous velocity of the droplet increased from ∼6.8 mm s−1, at room temperature (25 °C) to about ∼40 mm s−1, at a temperature of 65.7 °C on a wettability gradient surface. A force balance approach based on the driving and resistive forces have been developed and the resulting governing equation was used to explain the experimental results. The dominance of the contact line friction over the other two resistive forces was observed and a decreasing trend of the coefficient, ζ (from 0.15 Pa s to 0.0325 Pa s with a rise in mean temperature from 25 °C to 65.7 °C) was estimated. These results may assist devising strategies for electronic hot spot cooling where the dissipated heat can be effectively utilized to augment coolant droplet transport.Acknowledgements
The authors gratefully acknowledge the financial support provided by the Indian Institute of Technology Kharagpur, India [Sanction Letter no. IIT/SRIC/ATDC/CEM/2013-14/118, dated 19.12.2013].References
- F. Brochard, Langmuir, 1989, 5, 432–438 CrossRef CAS.
- A. T. Paxson and K. K. Varanasi, Nat. Commun., 2013, 4(1492), 1–8 Search PubMed.
- M. K. Chaudhury and G. M. Whitesides, Science, 1992, 256, 1539–1541 CAS.
- U. Thiele, K. John and M. Bär, Phys. Rev. Lett., 2004, 93, 027802 CrossRef.
- A. Checco, Phys. Rev. Lett., 2009, 102, 106103 CrossRef.
- A. Checco, B. M. Ocko, M. Tasinkevych and S. Dietrich, Phys. Rev. Lett., 2012, 109, 166101 CrossRef CAS.
- P. de Gennes, Rev. Mod. Phys., 1985, 57, 827–863 CrossRef CAS.
- D. Bonn, J. Eggers, J. Indekeu, J. Meunier and E. Rolley, Rev. Mod. Phys., 2009, 81, 739–805 CrossRef CAS.
- J. H. Snoeijer and B. Andreotti, Annu. Rev. Fluid Mech., 2013, 45, 269–292 CrossRef PubMed.
- M. Grunze, Science, 1999, 283, 41–42 CrossRef CAS.
- S. Daniel, M. K. Chaudhury and J. C. Chen, Science, 2001, 291, 633–636 CrossRef CAS PubMed.
- S. Morgenthaler, C. Zink and N. D. Spencer, Soft Matter, 2008, 4, 419–434 RSC.
- K. Ichimura, S. Oh and M. Nakagawa, Science, 2000, 288, 1624–1626 CrossRef CAS.
- A. Ghosh, R. Ganguly, T. M. Schutzius and C. M. Megaridis, Lab Chip, 2014, 14, 1538–1550 RSC.
- T. Franke, A. R. Abate, D. A. Weitz and A. Wixforth, Lab Chip, 2009, 9, 2625–2627 RSC.
- M. G. Pollack, A. D. Shenderov and R. B. Fair, Lab Chip, 2002, 2, 96–101 RSC.
- A. D. Sommers, T. J. Brest and K. F. Eid, Langmuir, 2013, 29, 12043–12050 CrossRef CAS PubMed.
- O. Bliznyuk, J. R. T. Seddon, V. Veligura, E. S. Kooij and H. J. W. Zandvliet, ACS Appl. Mater. Interfaces, 2012, 4, 4141–4148 CAS.
- H. Suda and S. Yamada, Langmuir, 2003, 19, 529–531 CrossRef CAS.
- R. S. Subramanian, N. Moumen and J. B. McLaughlin, Langmuir, 2005, 21, 11844–11849 CrossRef CAS PubMed.
- N. Moumen, R. S. Subramanian and J. B. McLaughlin, Langmuir, 2006, 22, 2682–2690 CrossRef CAS PubMed.
- H. Zhao and D. Beysens, Langmuir, 1996, 11, 627–634 CrossRef.
- S. Daniel and M. K. Chaudhury, Langmuir, 2002, 18, 3404–3407 CrossRef CAS.
- S. Daniel, S. Sircar, J. Gliem and M. K. Chaudhury, Langmuir, 2004, 20, 4085–4092 CrossRef CAS.
- J. Brzoska, F. Brochard-Wyart and F. Rondelez, Langmuir, 1993, 9, 2220–2224 CrossRef CAS.
- H. P. Jansen, K. Sotthewes, C. Ganser, C. Teichert, H. J. W. Zandvliet and E. S. Kooij, Langmuir, 2012, 28, 13137–13142 CrossRef CAS PubMed.
- M. L. Ford and A. Nadim, Phys. Fluids, 1994, 6, 3183–3185 CrossRef PubMed.
- V. Pratap, N. Moumen and R. S. Subramanian, Langmuir, 2008, 24, 5185–5193 CrossRef CAS PubMed.
- S. Mettu and M. K. Chaudhury, Langmuir, 2008, 24, 10833–10837 CrossRef CAS PubMed.
- J. D. Miller, S. Veeramasuneni, J. Drelich and M. R. Yalamanchili, Polym. Eng. Sci., 1996, 36, 1849–1855 CAS.
- M. Ramiasa, J. Ralston, R. Fetzer, R. Sedev, D. M. Fopp-Spori, C. Morhard, C. Pacholski and J. P. Spatz, J. Am. Chem. Soc., 2013, 135, 7159–7171 CrossRef CAS PubMed.
- B. R. G. Cox, J. Fluid Mech., 1986, 168, 169–194 CrossRef.
- A. Ahmadi, J. F. Holzman, H. Najjaran and M. Hoorfar, Microfluid. Nanofluid., 2010, 10, 1019–1032 CrossRef.
- A. Ahmadi, H. Najjaran, J. F. Holzman and M. Hoorfar, J. Micromech. Microeng., 2009, 19, 065003 CrossRef.
- T. D. Blake and J. De Coninck, Adv. Colloid Interface Sci., 2002, 96, 21–36 CrossRef CAS.
- T. D. Blake, J. Colloid Interface Sci., 2006, 299, 1–13 CrossRef CAS PubMed.
- A. Ahmadi, K. D. Devlin and M. Hoorfar, Microfluid. Nanofluid., 2011, 12, 295–305 CrossRef.
- S. Ray, R. Sedev, C. Priest and J. Ralston, Langmuir, 2008, 24, 13007–13012 CrossRef CAS PubMed.
- D. Duvivier, T. D. Blake and J. De Coninck, Langmuir, 2013, 29, 10132–10140 CrossRef CAS PubMed.
- B. A. Carlson, G. Bellani and G. Amberg, Linné Flow Centre, KTH Mech. Stock, Sweden, 2011, 197–210.
- M. Chakraborty, A. Chowdhury, R. Bhusan and S. Dasgupta, arXiv: 1504.02567, 2015.
- R. Vellingiri, N. Savva and S. Kalliadasis, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 036305 CrossRef.
- A. M. Cazabat and G. Guéna, Soft Matter, 2010, 6, 2591–2612 RSC.
- M. Chakraborty, A. Ghosh and S. DasGupta, RSC Adv., 2014, 4, 1074–1082 RSC.
- M. J. de Ruijter, J. De Coninck, T. D. Blake, A. Clarke and A. Rankin, Langmuir, 1997, 13, 7293–7298 CrossRef CAS.
- M. J. De Ruijter, T. D. Blake and J. De Coninck, Langmuir, 1999, 15, 7836–7847 CrossRef CAS.
- J. Z. Chen, S. M. Troian, A. a. Darhuber and S. Wagner, J. Appl. Phys., 2005, 97, 014906 CrossRef PubMed.
- A. Prevost, E. Rolley and C. Guthmann, Phys. Rev. Lett., 1999, 83, 348–351 CrossRef CAS.
- E. Rolley and C. Guthmann, Phys. Rev. Lett., 2007, 98, 166105 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra00469a |
| This journal is © The Royal Society of Chemistry 2015 |