Mechanism evolution for the oxidative dehydrogenation of ethyl benzene to styrene over V₂O₅/TiO₂ catalyst: computational and kinetic approach

Abstract

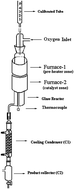
A kinetic study of the oxidative dehydrogenation of ethylbenzene has been performed in a differential flow reactor over a V₂O₅/TiO₂ catalyst. The partial pressures of ethylbenzene and oxygen were varied and rates were measured for the formation of styrene. Kinetics studies reveal that the mechanism of the reaction is of the “Mars Van Krevelen Redox” type. The rate equation deduced, assuming a steady state involving a two stage oxidation–reduction process, represented the data most satisfactorily. The catalyst has been synthesized by a method similar to a solution combustion method and characterized using FT-Raman and powder XRD methods. DFT level computational studies provided a deep insight for the reaction mechanism at the molecular level. According to our calculations ethylbenzene first dissociatively adsorbs over the catalyst and produces an ethylbenzene radical which subsequently adsorbs on the vanadyl group or bridging oxygen V–O–V or bridging oxygen V–O–Ti. The adsorbed radical further loses an H atom to produce styrene. The catalyst is regenerated by molecular oxygen.

---

1. Introduction

Styrene is an extremely important chemical used extensively in the manufacture of numerous polymers and copolymers, such as polystyrene, acrylonitrile-butadiene-styrene (ABS), styrene-acrylonitrile (SAN), styrene-butadiene latex, and styrene-butadiene rubber.¹ Styrene is used for the production of synthetic rubber which is in some respects superior to those of natural rubber.² Its derivatives such as styrene oxide can be reduced to bulk perfume 2-phenyl ethanol.³

The conventional commercial process for production of styrene by dehydrogenation of ethyl benzene (EB) over Fe–K–Cr catalyst uses steam and is energy intensive.⁴ Attempt has been made to find different catalyst and co-oxidants to reduce the process cost. Catalysts such as bimetallic nitride, supported metallic nitride, CeO₂ in carbon nano tube; Mg supported iron oxide, Fe-doped MgAl₂O₄ spinel^5–8 have been used for dehydrogenation. Oxidative dehydrogenation for the production of unsaturated products like propylene or styrene in the current area of research because of its exothermic nature as heat generated may be used in other heat consuming process.⁹

Supported vanadia systems are complex mixed oxides posses interesting catalytic properties which depend on a variety of factors including preparation method, thermal treatment, and nature of support.¹⁰

VO_x/TiO₂ attracted attention as it shows superior performance over various catalyst i.e. vanadia supported over silica, alumina and titania for various oxidation reactions.¹¹

Oxidative dehydrogenation reaction has also been studied extensively over vanadium oxide supported over titanium, silica, alumina, zirconia and various mixed oxide due to their high thermal stability, easiness in regenerative ability with high conversion and selectivity.^9,12,13

Kinetics study of oxidative dehydrogenation (ODH) of saturated hydrocarbons to unsaturated hydrocarbons is of great importance because of (a) commercial usefulness of unsaturated hydrocarbons and their derivatives such as epoxides³ (b) prediction of mechanism of the reaction and (c) reactor design. ODH of ethyl benzene (EB) produces styrene (S) which can be further oxidized to styrene oxide, both being monomers for polystyrene and polystyrene oxide respectively. There are few reports over kinetic modeling for the oxidative dehydrogenation reactions of alkane^14,15 but there is no reports on kinetic modeling of ODH of ethyl benzene over titania supported vanadia.

In recent years density functional theory has been applied to glean information of the mechanism of ODH reactions.^16–18 To the best of our knowledge there is no report on the mechanism of ODH of EB based on DFT Theory. The present problem of the kinetic and DFT study for ODH of EB over titania supported vanadia was therefore undertaken to (1) deduce the rate law for the reaction (2) know the mechanism at molecular level (3) estimate the activation energy of the reaction and (4) elucidation of the various reaction pathways.

2. Experimental methods

2.1. Catalyst preparation and characterization

A TiO₂ supported V₂O₅ catalyst (TV) in the molar ratio 90 : 10 was used in the present study. Precursors for TiO₂ and V₂O₅ were TiO(NO₃)₂ and ammonium meta vanadate respectively. Titanyl nitrate was prepared by treating TiO(OH)₂ with nitric acid which was obtained by hydrolysis of tertiary butyl orthotitanate (TBOT) with water. Two different solutions of (a) titanyl nitrate and (b) ammonium meta vanadate with citric acid were prepared. Solutions (a) and (b) were mixed and heated on a hot plate to get a dry gel. The gel was calcined for six hour in muffle furnace at 823 K to get the catalyst.

The catalyst was characterized by powder-XRD and FT-Raman methods. The powder-XRD measurements were carried out using Bruker D8 Advance X-ray diffractometer using a sealed tube and Cu K-alpha line of 0.145 nm. The X-rays were detected using a fast counting detector based on silicon strip technology (Bruker Lynx Eye detector).

The Raman spectra was recorded in the range 100–1200 cm⁻¹ with the help of a Labram HR800 micro Raman spectrometer using 488 nm wavelength and Ar+ laser source at the energy of 2.53 eV.

2.2. Study of ODH for ethyl benzene

The kinetic experiments were performed in a fixed bed differential down flow Pyrex glass tubular reactor (Fig. 1). The upper part act as pre-heater zone and lower half act as reactor, where catalyst was loaded in between two plugs of Pyrex glass wool. The reactant has been passed with the help of down flow reactor at different flow rate. The flow of oxidant (air) was controlled with the help of air pump and flow meter. The liquid product were condensed with the help of cold water condenser, collected in a receiver and analyzed by Schimadzu 14B Gas Chromatograph using SE-30 column and FID detector.

Fig. 1 Experimental set up for study of the reaction.

The first few runs were taken to check out the kinetic limiting condition, i.e. conversion of ethyl benzene for two different amount of the catalyst is almost same. It was found that at 1.0 g of the catalyst loading the graph of EB conversion became linear indication that catalyst loading has no effect on the rate of reaction.

3. Computational methods

All the DFT calculations were performed using Gaussian 09W suite¹⁹ and B3LYP functionals.²⁰ We had used LANL effective core potential (ECP) with double zeta potential (Lanl2dz) for optimization of reactants, products, and transition state. This basis set has overall combination of ECP and valence basis set.²¹ The ECP parameters for vanadium atom have been derived from atomic wave functions obtained by all-electron non-relativistic Hartree–Fock calculations. The light atoms (carbon, hydrogen and oxygen) were optimized using 6-311G(d, p) basis set while for heavy atoms (vanadium and titanium atom) we had used lanl2dz basis set. Modeling of transition state structure calculation QST2/QST3 keyword has been used.²⁰ At many places the optimization of transition state was achieved directly also.²² Vibrational frequencies were calculated for the optimized geometries to identify the nature of the reactant or product (no imaginary frequency) and TS structure (one imaginary frequency). RB3LYP was used for singlets and UB3LYP for higher multiplicities. In UB3LYP calculations separate α and β orbitals are computed.¹⁹ The calculation for singlet diradical system has been performed using “guess = (mix, always, densitymix)” keywords. This keyword helps to predict atomic spin density (Unpaired electron density), if alpha and beta electron densities were situated over different atoms i.e. singlet diradical system. We had also calculated the “open shell vs. closed shell correction term” over 6-311G(d, p) basis set as it includes all electron calculation. This term is used to eliminate the error which may arise due to closed shell calculations.

The enthalpy and the activation energies were calculated at the reaction temperature as described by J. W. Ochterski.²³ The adsorption energy (E_ads) was calculated as^24,25

E_ads = E_{(adsorbate−substrate)} − (E_adsorbate + E_substrate).

The chemical reactivity of various oxygen atoms has been described in the form of Fukui functions. We have also calculated the Fukui functions for the different type of oxygen atoms present in our catalyst model.²⁶

4. Result and discussion

4.1. Raman and XRD analysis

The appearance of a sharp peak at 145.2 cm⁻¹ in FT-Raman spectrum suggests a monolayer distribution of V₂O₅ over support.²⁷

Rest three major peaks in the spectrum at 283.4, 436.4, 607.9 cm⁻¹ belongs to support i.e. TiO₂.¹² The stretching vibration of vanadyl V=O appears at 995 cm⁻¹. The skeleton bent vibration at 145.2 cm⁻¹ and the stretching vibration of vanadyl V=O group at 995 cm⁻¹ support the perfect layer-type structure of V₂O₅.²⁷ The FT-Raman spectrum of the catalyst is shown in Fig. 2.

Fig. 2 The FT-Raman spectrum of the catalyst.

The XRD pattern of the catalyst is shown in Fig. 3 in which identified planes has been labeled.^28,29 Peak at 24.5 shows presence of polymeric layered vanadia, while peak at 27.6 is for anatase titanium oxide. Peaks at 2θ value of 36.2, doublet at 54.2 and 56.5 belongs to anatase phase. Peaks at 41.2 and 67.2 with low intensity are for rutile phase which confirms that there is some rutile phase (TiO₂) also present along with the anatase (TiO₂).

Fig. 3 The XRD pattern of the catalyst. R-rutile phase, A-anatase phase.

4.2. Kinetic studies

The study of initial rate data provides a first approximation in understanding the dependency of the reaction rate on individual parameters. Liquid samples were collected after 1/2 h (30 min) when equilibrium conversion was reached and analyzed on gas chromatograph for concentrations of product and reactant distribution in whole reaction.

In order to minimize external diffusion the ethyl benzene conversion was measured as a function of catalyst amount at constant hydrocarbon–oxygen ratio in the feed. External diffusion was taken to be negligible when plot becomes almost parallel to the catalyst axis (Fig. 4).

Fig. 4 Effect of weight of catalyst on conversion.

All data collected at low conversion which allows easier data processing and differential condition. The concentration of gaseous reactants was expressed in terms of their partial pressure. The variation in partial pressure has been adjusted by a passing the inert gas (nitrogen) making total pressure constant. The rate was defined as

Data were analyzed using least square method and a computer program written in FORTRAN. Analysis of the reaction mixture was repeated time to time to ensure that material balance, which was more than 95% all the time.

4.2.1 Catalyst deactivation. To study the catalyst deactivation, repeated experiments were performed without catalyst regeneration between two consecutive run. To minimize the effect of catalyst/feed ratio, weight of catalyst and moles of EB were kept constant. It was found that the yield of styrene decreased if there is no catalyst regeneration between two consecutive run.

If we regenerate the catalyst then the yield is also nearly same in any two run which shows that there is need of catalyst regeneration after each run. This also confirms the redox nature of the catalyst as it get reduced after first run which require to oxidized by the air (catalyst regeneration step).

4.2.2 Effect of partial pressure of ethyl benzene. Effect of partial pressure of ethyl benzene on the initial rate of formation of styrene with 1.0 g of the catalyst at constant partial pressure of oxygen is shown in Fig. 5. The rates initially increased with increase in the partial pressure of ethyl benzene. However, the rates tend towards limiting rates at higher partial pressure.

Fig. 5 Effect of partial pressure of ethyl benzene. Calculated rates obtained by putting the values of k₁, k₂ in rate law of model-1 shown in Table 1.

4.2.3 Effect of partial pressure of oxygen. Effect of partial pressure of oxygen on the initial rate of reaction with 1.0 g of the catalyst shows Fig. 6 that initial rate increases with increase in partial pressure, however the rate of decreases after the flow rate of 60 ml H⁻¹ for oxygen.

Fig. 6 Effect of partial pressure of oxygen.

4.3. Evaluation of kinetic data

Most studies on kinetics and mechanism of oxidations, ammoximation and oxidative dehydrogenation over V₂O₅ catalyst are based on Mars-Van-Krevelen mechanism. According to this mechanism the catalyst is first reduced by the hydrocarbon (EB) and then the reduced catalyst is re-oxidize by the molecular oxygen. We considered a two stage as well as three state redox mechanisms for the reaction and are listed in Table 1.

Table 1 Redox models tested for oxidative dehydrogenation of ethyl benzene to styrene^a

Model	Mechanism	Rate equation
a R = rate of formation of styrene, k1, k2 or k3 = rate constants, PO = partial pressure of oxidant, PEB = partial pressure ethyl benzene, ST = styrene, Sred = reduced surface, Sox = oxidized surface. The rate law for these two mechanisms can be derived as follows.
1	Two stage mechanism
2	Three stage mechanism

---

4.3.1 Two step mechanism.

Rate of reduction of surface = k₁S_oxP_EB

Rate of oxidation of surface = k₂(1 − S_ox)P_O

Here, k₁ and k₂ are constants.

At steady state condition,

k₂(1 − S_ox)P_O = k₁S_oxP_EB

k₂P_O = (k₂P_O + k₁P_EB)S_ox

Rate of reaction = k₁P_EBS_ox (1)

Or

4.3.2 Three stage mechanism.

Applying steady state approximation for TS − S_red and S_red

k₁P_EBS_ox = k₂[TS − S_red]

k₂[TS − S_red] = k₃P_OS_red

1 = S_ox + S_red + TS − S_red

These equations were linearized and solved for constants k₁, k₂ or k₃. Since the processes are physical, the constants must be positive. Therefore model 2 with negative constant was rejected. Further justification for the model-1 was found from the plot of observed rate and calculated rates against P_EB (Fig. 5). Reasonable matching of the observed rates with calculated rates confirm the correctness of model-1.

Further confirmation of the redox model and transition state structure was made with the help of density functional theory employing Gaussian 09W software and is detailed in the next section.

4.4. Computational studies

4.4.1 The catalyst structure and its optimization. The catalyst structure was optimized assuming monolayer distribution over support Fig. 7. The monolayer distribution was confirmed in previous section. The cluster in Fig. 7 can be considered as an equivalent structure of the top surface layer of the catalyst. The structure reveals that there are three type oxygen namely O1 (Vanadyl group V=O), O2 (bridging oxygen V–O–V) and O3 (bridging oxygen V–O–Ti) (Fig. 8).

Fig. 7 Model showing monolayer distribution of V₂O₅ over TiO₂.

Fig. 8 The catalyst model used for calculation and it represents the all type of oxygen atoms.

This cluster is quite large for calculation as we are using a large basis set for calculations. We had cut this cluster from mid to a smaller size suitable for computation and containing the essential moieties for the reaction containing two vanadyl group (V=O) site, one the V–O–V bridging site and four V–O–Ti bridging site representing all type of oxygen present in bulk system.

4.4.2 The evidences of MVK mechanism and identification of active site. Most of the mechanisms suggested for oxidative dehydrogenation of organic compounds over supported vanadium oxide catalysts are based on Mars-Van-Krevelen redox mechanism²⁷ detailed in previous Section 4.2 and the C–H bond activation step is the rate determining step.²⁸

A reaction is always accompanied with change in its energy and electronic state, therefore a study of the electronic structure may give some insight of the mechanism of the reaction. Since O1, O2 and O3 site posses' different electron density, hence their behavior towards the reactant (EB) will also be different. The nucleophilicity of these oxygen atoms are expressed in terms of Fukui functions.²⁵ Their calculated nucleophilicity are 0.06, 0.004 and 0.02 for O1, O2 and O3 site respectively. We can expect their reactivity proportional to their nucleophilicity.

4.4.3 Molecular adsorption of ethyl benzene. The catalyst has three different type of oxygen out of which O1 has highest reactivity. On each of the atom we get positive heat of adsorption which shows that ethyl benzene does not form a molecular adsorption state on the surface or only physisorbs over catalyst very weakly. The positive adsorption energies are due to underestimation of physisorption energy because DFT calculations consider only electrostatic interaction part of van der Waals interactions. Low values of heat of adsorption rule out role of physical adsorption in activation of C–H bond suggesting requirement of high temperature chemisorptions for the activation of C–H bond.

4.4.4 Activation of C–H bond. Absence of strong acidic or basic site at the catalyst, rules out the possibility of reaction to proceeds as acidic or basic mechanism. The previous DFT calculations on ODH of alkanes suggest that the abstraction of a hydrogen atom by the catalyst is slow and rate determining step.²⁴ In our calculation C–H bond abstraction is possible from methyl as well as methylene groups of EB. The bond enthalpy for methyl hydrogen atom is 420 kJ mol⁻¹ while for methylene it is 401 kJ mol⁻¹, suggesting that the first hydrogen abstraction will be from methylene group.²⁴ In our calculation we consider, radical mechanism. In radical mechanism EB dissociatively adsorbs on the surface to form an oxide like structure and a hydroxyl group, consuming two lattice oxygen atoms.

4.4.5 Radical mechanism. Most of the articles on DFT of ODH of hydrocarbons suggest a radical based mechanism.^{16–18,24,25} In this mechanism first a methylene H atom is removed as a radical gets attached to vanadyl oxygen leading to the formation of a hydroxyl group and secondary ethyl benzene radical (˙C₈H₉) free in gas phase which subsequently gets adsorbed on O1, O2 or O3 site. The transition state (TS) structure for first hydrogen atom abstraction is shown in Fig. 1 (ESI†). The radical nature of TS structure is confirmed by considering singlet diradical system.^30–32 The TS structure is featured by lengthening of C–H bond while shortening of OH distance. The activation energy for this step is 41.4 kcal mol⁻¹. For second H abstraction EB radical may now get adsorbs on one of the O1, O2, O3 sites.
4.4.5.1 Adsorption at O1 site. If the radical adsorbed on nearby O1 site then it has three possibilities for second H atom removal, viz. O1 (V–OH), O2 or O3 site. Second H abstraction by vanadyl hydroxyl (V–OH) group involves removal of methyl hydrogen followed by desorption of water molecule, leading to a vacancy on the vanadium atom. The TS structure for this step is shown in Fig. 2 (ESI†). In TS structure the O–H bond distance is 1.17 Å. The activation energy for this step is 90.5 kcal mol⁻¹.

The TS structure for second H abstraction by O2 site is shown in Fig. 3 (ESI†). This structure reveals the formation of hydroxyl group with bridging oxygen atom where OH bond distance is 1.79 Å. Because of high activation energy (134.3 kcal mol⁻¹) this possibility is ruled out.

The methyl H atom removal by O3 site need special attention as it is bridged with titanium atom in the catalyst and hence it has some different feature like higher nucleophilicity with respect to bridging oxygen O2. Due to its higher nucleophilic nature, it is more reactive towards H abstraction in comparison to O2.²⁶ This possibility with activation energy of 28.3 kcal mol⁻¹, which is less than the other two sites (V–OH and O2) seems to be most probable possibility for second H atom removal. The TS geometry is presented in Fig. 4 (ESI†) in which the OH bond distance is 1.39 Å.

4.4.5.2 Adsorption at O2 site. In this case the radical formed gets adsorbed over O2 site. After adsorption, O2 site oxygen become triply coordinate and due to its instability one V–O bond gets ruptured. The activation energies for second H atom abstraction by different sites are listed in Table 2. From Table 2 it can be concluded that O3 site will be preferred for second H abstraction. The TS structure of all these possibilities is given in Fig. 5 (ESI†).

Table 2 Radical adsorption sites and second H abstraction site along with corresponding activation energies

Radical adsorption site	Second H abstraction site and corresponding activation energy (kcal mol^−1)
O1	V–OH	O2	O3
	90.5	134.3	28.3
O2	O1	O3	V–OH
	87.85	39.6	76.9
O3	O1	O2	O3
	44.7	16.3	33.2

---

4.4.5.3 Adsorption at O3 site. In this case the radical formed get adsorbed over O3 site which is quite less hindered in comparison to O2 sites and hence more stable. The activation energies for second H atom abstraction by O1, O2, O3 sites are listed in Table 2. Their TS geometries are shown in Fig. 6 (ESI†). The lowest activation energy was found to be 16.3 kcal mol⁻¹ associated with O2 site.

The overall PES diagram showing formation of EB radical and its subsequent adsorption on O1, O2, O3 site is shown in Fig. 7 (transition state as green and intermediates as blue). The lowest activation energy was found 16.3 kcal mol⁻¹ associated with adsorption of radical at O3 site followed by second H atom removal by O2 site. The overall energy for the reaction is 41.4 kcal mol⁻¹.¹⁶ The experimental activation energy from Arrhenius equation was found to be 40.54 kcal mol⁻¹ (Fig. 9).

Fig. 9 The overall potential energy diagram for various routes.

4.5. Formation and desorption of product from reaction site

Desorption energy of the styrene from the catalyst surface is calculated to be exothermic in nature with ΔH value of 11.2 kcal mol⁻¹. It may be recalled that the lowest activation energy for first H atom removal from EB is by O1 site and the second H atom abstraction from ethylbenzene radical is found to be by O2 site. The catalyst gets regenerated after removal of water from the two OH groups situated at these O1 and O2 sites. It is also possible that H atom of O2 site migrate to O1 (V–OH) site and facilitate the removal of water thus creating an oxygen vacancy at the vanadium site. The reoxidation of the catalyst by molecular oxygen is quite facile, fast and doesn't seem to be rate determining step.¹⁶

5. Conclusion

Mechanism of oxidative dehydrogenation of ethylbenzene to styrene over catalyst has been explained with the help of adjunct kinetic study as well as density functional theory calculations. The investigations suggest that, reaction proceeds through two stage redox mechanism. There is appropriate matching of experimental and calculated data which shows the correctness of the model. The activation energy of the first H atom abstraction leading to ethyl benzene radical is 41.4 kcal mol⁻¹ and this is the rate determining step also. Further, the ethylbenzene radical formed in the first step may adsorb on O1, O2, and O3 site. This radical can further loose methyl hydrogen with the help of O1, O2 or O3 site to produce styrene. The adsorption of radical at O3 site and second H atom removal by O2 seems to be lowest energy path for second H abstraction. The activation energy for over all reaction is 41.4 kcal mol⁻¹ against the experimental value of 40.54 kcal mol⁻¹. Geometries of all the transition states along with the activation energies are reported.

References

1. R. R. Miller, R. Newhook and A. Poole, Crit. Rev. Toxicol., 1994, S1–S10,  DOI:10.3109/10408449409020137.
2. G. Egloff, US Pat., Application Number: US43048242A, Publication Date: 05/22/1945, Filing Date: 02/11/1942.
3. G. D. Yadav and Y. S. Lawate, Ind. Eng. Chem. Res., 2013, 52, 4027–4039,  DOI:10.1021/ie302587j.
4. K. K. Kearby, in Catalysis, ed. P. H. Emmett, Reinhold, New York, 1955, vol. 3, ch. 10.
5. J. Madhavi, PhD thesis, Indian Institute of Chemical Technology and University of Hyderabad, 2014.
6. R. Rao, Q. Zhang, H. Liu, H. Yang, Q. Ling, M. Yang, A. Zhang and W. Chen, J. Mol. Catal. A: Chem., 2012, 363, 283–290.
7. M. D. C. Rangel, A. P. D. M. Monteiro, S. G. Marchetti, S. B. Lima and M. D. S. Ramos, J. Mol. Catal. A: Chem., 2014, 387, 147–155.
8. M. Ji, X. Zhang, J. Wang and S. E. Park, J. Mol. Catal. A: Chem., 2013, 371, 36–41.
9. A. Verma, R. Dwivedi, P. Sharma and R. Prasad, RSC Adv., 2014, 4, 1799–1807.
10. A. Adamski, Z. Sojka, K. Dyrek, M. Che, G. Wendt and S. Albrecht, Langmuir, 1999, 15, 5733–5741.
11. V. I. Avdeev and A. F. Bedilo, J. Phys. Chem. C, 2013, 117, 2879–2887,  DOI:10.1021/jp311322b.
12. S. Kumarsrinivasan, A. Verma and C. S. Gopinath, Green Chem., 2012, 14, 461–471.
13. A. Christodoulakis, M. Machli, A. Lemonidou and S. Boghosian, J. Catal., 2004, 222, 293–306.
14. S. A. Ghamdi, J. Moreira and H. D. Lasa, Ind. Eng. Chem. Res., 2014, 53, 15317–15332,  DOI:10.1021/ie404064j.
15. A. Bottino, G. Capannelli, A. Comite, S. Storace and R. D. Felice, Chem. Eng. J., 2003, 94, 11–18.
16. Y. J. Du, Z. H. Li and K. N. Fan, J. Mol. Catal. A: Chem., 2013, 379, 122–138.
17. G. L. Dai, Z. H. Li, J. Lu, W. N. Wang and K. N. Fan, J. Phys. Chem. C, 2012, 116, 807–817.
18. P. Sharma, R. Dwivedi, R. Dixit, M. S. Batra and R. Prasad, J. Comput. Methods Mol. Des., 2014, 4, 1–14.
19. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, V. H. T. Nakai, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 (Revision B.01), Gaussian, Inc., Wallingford, CT, 2010.
20. J. B. Foresman and E. A. Frisch, Exploring chemistry with electronic structure methods, Gaussian Inc, Pittsburgh, PA, 2nd edn, 1996.
21. W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 270–283.
22. L. Barbossa, Theoretical studies of nitrile hydrolysis by solid acid catalyst, PhD thesis, Technische Universiteit Eindhoven, 2000, Proefschrit, ISBN: 90-386-2811-0, http:\\alexandria.tue.nl/extra2/200000156.pdf.
23. Thermochemistry in Gaussian, J. W. Ochterski, http://www.gaussian.com/g_whitepap/thermo.htm.
24. H. Fu, Z. P. Liu, Z. H. Li, W. N. Wang and K. N. Fan, J. Am. Chem. Soc., 2006, 128, 11114–11123,  DOI:10.1021/ja0611745.
25. N. H. Nguyen, T. H. Tran, M. T. Nguyen and M. C. Le, Int. J. Quantum Chem., 2010, 110, 2653–2670.
26. E. G. Leware, Computational Chemistry: Introduction to the Theory and Applications of Molecular and Quantum Mechanics, Springer, 2nd edn.
27. Q. Su, X. Q. Liu, H. L. Ma, Y. P. Guo and Y. Y. Wang, J. Solid State Electrochem., 2008, 12, 919–923,  DOI:10.1007/s10008-008-0515-5.
28. http://jes.ecsdl.org/content/159/8/A1135/F5.large.jpg.
29. http://oasys2.confex.com/acs/235nm/techprogram/images/1140253-1.gif.
30. N. Turra, U. Neuenschwander and I. Hermans, ChemPhysChem, 2013, 14, 1666–1669.
31. U. Neuenschwander, E. Meier and I. Hermans, ChemSusChem, 2011, 4, 1613–1621.
32. M. J. Cheng, K. Chenoweth, J. Oxgaard, A. V. Duin and W. A. Goddard, J. Phys. Chem. C, 2007, 111, 5115–5127.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra00446b

---