The effect of artificial grain boundaries on magneto-transport properties of charge ordered-ferromagnetic nanocomposites
Kalipada Das*,
B. Satpati and
I. Das
Saha Institute of Nuclear Physics, 1/AF, Bidhannagar, Kolkata-700064, India. E-mail: kalipada.das@saha.ac.in
First published on 3rd March 2015
Abstract
Nanocomposites of charge ordered insulating Pr0.67Ca0.33MnO3 (PCMO) and ferromagnetic metallic La0.67Sr0.33MnO3 (LSMO) nanoparticles have been prepared by chemical synthesis. Transport and magneto-transport properties of nanocrystalline LSMO and the PCMO–LSMO nanocomposites have been studied in detail. At a low temperature region, upturn of resistivity for both the compounds was observed. The upturn of resistivity is strongly influenced by the external magnetic field. The results are analyzed considering intergranular spin polarized tunneling model. Our study reveals that spin polarized tunneling (SPT) is the dominant mechanism leading to the rise in resistivity especially below T = 60 K. It also indicates that SPT through the grain boundary is significantly modified in nanocomposite compounds, which leads to the enhancement of magnetoresistance and low field magnetoconductance compared to LSMO nanoparticles.
1. Introduction
During the last two decades, enormous attention has been paid to study the physical properties of doped perovskite manganite.1–10 Due to the presence of a lot of intriguing phenomena, such as colossal magnetoresistance effect, metal insulator transition, charge ordering and magnetic field induced metamagnetic transition in doped manganites, this field has become an intense field of current research. Except the polycrystalline bulk compounds, another field of growing interest of doped manganites is the observation of fascinating behavior at lower dimensions. It is well documented that the physical properties of doped manganites are greatly modified in their nanostructure forms.3–6 Effects of internal stress by the variation of trivalent ion radius or particle size reduction, grain boundaries, grain size and crystallinity on magnetoresistance of doped manganites has been extensively studied.11–15 Many attempts have been made to explain the electrical transport and magnetotransport behavior of these compounds. Assuming that the electrical transport in a material is dominated by two different kinds of parallel connected channels (depending upon the temperature and magnetic field), Andres et al. proposed a macroscopic model.16 In their model, the electronic transport and magnetoresistance are determined by the relative weight of the channels. Another model was proposed by Wagner et al. where negative MR is scaled with Brillouin function in the ferromagnetic region.17 To describe the electronic transport especially at the low temperature region, Hwang et al. proposed the spin polarized tunneling model in polycrystalline compounds through the grain boundaries.18 This model is now widely used to understand the adequate elucidation of electronic transport and the influence of magnetic field on it for polycrystalline compounds at low temperature.19–22Generally, for granular systems, the effect of grain boundaries and width of the barrier on electronic and magnetotransport properties are significant.23,24 Sharp drop of magnetoresistance at very low field region correspond to the spin dependent effect due to different orientations of magnetization of neighboring grains. However, at the high magnetic field regime, almost linear behavior is commonly observed, which is connected with the magnetic behavior of the grain boundary that can be different from the bulk material.25
In our present study, we report the magnetic, electronic and magneto-transport behavior of the LSMO nanoparticles and PCMO–LSMO nanocomposites in detail. Low temperature upturn in resistivity for both compounds are attempted for description using various models. The enhancement of magnetoresistance and low field magnetoconductance in nanocomposites are analyzed taking into account spin polarized tunneling (SPT) through grain boundary at a lower temperature.
2. Experimental section
2.1. Sample preparation, characterization and measurements
Nanocrystalline LSMO and nanocomposites have been prepared by the well-known sol–gel route. For the preparation of nanocrystalline LSMO, the starting elements were pre-heated La2O3, Sr(NO3)2 and MnO2 with the purity greater than 99.99%. The appropriate amount of oxides have been converted to their nitrate form by using nitric acid. Suitable amount of citric acid was added to the clear water solution of the nitrates. Subsequently, the mixture was slowly evaporated at 80–90 °C by using a water bath until the gel was formed. A black porous powder was formed by the decomposition of the gel. After pelletizing the black powder, it was heat treated for 4 hours at 950 °C to get nanocrystalline LSMO.For the preparation of the nanocomposites, first we prepared PCMO nanoparticles by the abovementioned route using preheated Pr6O11, CaCO3 and MnO2. A crystalline nanostructure was formed by heat treatment of the decomposed gel at 950 °C for 4 hours. Moreover, a suitable amount of the LSMO gel (depending upon the required thickness (in present study it is ∼10 nm)) was prepared by the same route and the prepared PCMO nanoparticles were mixed in the LSMO gel at the last stage of the gel formation and stirred continuously. Finally, one part of the pelletized black porous powder was heat treated at 900 °C for 4 hours (nanocomposite-1) and another part at 850 °C for 4 hours (nanocomposite-2).
Room temperature X-ray diffraction study was carried out for four prepared samples (LSMO, PCMO, nanocomposite-1 and nanocomposite-2) by using a Rigaku diffractometer in Bragg–Brentano geometry using Cu-Kα source having a wavelength of 1.54 Å. Transmission electron microscopy (TEM) measurements were performed using FEI, Tecnai G2 F30, S-Twin microscope operating at 300 kV. The microscope was equipped with a high-angle annular dark field detector from Fischione (model 3000) and a scanning unit. The compositional analysis was performed using energy dispersive X-ray spectroscopy (EDS, EDAX Inc.) and energy-filtered TEM (EFTEM) measurements using Gatan imaging filter, Quantum SE (model 963) attachment in the same microscope. The sample was dispersed in isopropanol using ultrasonic bath, mounted on a carbon coated Cu grid, dried, and used for TEM measurements.
Electronic transport and magneto-transport properties of LSMO nanoparticles and nanocomposite compounds have been performed by the usual four probe method. Magnetization as a function of magnetic field measurements is carried out using superconducting quantum interference device (SQUID) (Quantum Design).
3. Experimental results and discussion
X-ray diffraction measurements at room temperature indicate the single phase nature of the LSMO and PCMO nanoparticles. In case of the nanocomposites, no additional phase was found except their parent compounds (shown in Fig. 1). The grain size of the LSMO and PCMO were estimated from the X-ray line width broadening (excluding the instrumental broadening) and it was found to be ∼28 nm and ∼46 nm for LSMO and PCMO, respectively. The lattice parameters of the nanostructure compounds were estimated by utilizing Rietveld refinement technique (using FULLPROF program). According to the earlier reports on the structural properties of doped manganites, bulk LSMO and PCMO possess R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c and Pnma space group symmetry, respectively.26 In the present case, the X-ray diffraction pattern of LSMO and PCMO nanoparticles was indexed considering the R
c and Pnma space group symmetry, respectively.26 In the present case, the X-ray diffraction pattern of LSMO and PCMO nanoparticles was indexed considering the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c and Pnma space groups. The obtained lattice parameters of the parent compounds (LSMO and PCMO) are summarized in Table 1. However, for nanocomposites, because the space groups of the parent compounds are very close to each other, it is difficult to distinguish the two phases from X-ray diffraction patterns.
c and Pnma space groups. The obtained lattice parameters of the parent compounds (LSMO and PCMO) are summarized in Table 1. However, for nanocomposites, because the space groups of the parent compounds are very close to each other, it is difficult to distinguish the two phases from X-ray diffraction patterns.
| Compound | Space group | Lattice parameters (Å) |
|---|---|---|
| LSMO | R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
a = 5.482 |
| b = 5.482 | ||
| c = 13.359 | ||
| PCMO | Pnma | a = 5.434 |
| b = 7.679 | ||
| c = 5.431 |
The nanostructured compounds were further characterized by TEM measurements. In our present report, one representative high resolution TEM (HRTEM) image from nanocomposite-1 sample is shown in Fig. 2. In order to understand the nanocomposite nature of this structure, we have analyzed HRTEM data carefully. Here, we have measured lattice spacing from different regions as marked by red and blue boxes and the corresponding Fourier filtered images are shown by numbered boxes. The measured lattice spacing from all the red regions is 2.75 Å and from the blue region is 3.81 Å. The interplanar spacing of orthorhombic LSMO (112) is 2.75 Å (JCPDS card # 53-0057) and that of orthorhombic PCMO (101) is 3.81 Å (JCPDS card # 89-0795). Thus, the measured lattice spacing from different regions indicate the formation of nanocomposite structure. However, one should note that this lattice spacing of LSMO may match with some other spacing of PCMO with different crystal symmetry.
Fig. 2(a) further shows that the complete structure is an interconnected grain. The fast Fourier transform (FFT) image in Fig. 2(b) is from a region marked by a dotted green box, and the magnified image in Fig. 2(c) is from a yellow dotted box where one can see that two crystal grains are oriented by a small angle and between them there is an amorphous layer. We have investigated several such regions of LSMO and observed that in most cases crystals grains are separated by such amorphous layers. Amorphous layer was confirmed by tilting the specimen in different zone axes.
We have analyzed the effect of enhanced grain boundaries in case of nanocomposites on transport and magneto-transport properties in the later part of this article. To investigate the chemical composition of the nanocomposite structures, we have performed high-angle annular dark field (HAADF) analysis. Fig. 3(a) shows the STEM-HAADF image and this Z-contrast image also shows nanocomposite nature but possibility of different grain thickness (and hence brighter contrast due to higher thickness) cannot be ruled out. Fig. 3(b) is the corresponding EDX spectrum from area 1, indicating the presence of all the constituent elements of the PCMO–LSMO nanocomposite structure. The Cu signal is due to the Cu-grid. To confirm the nanocomposite nature, we have done line scan analysis, which clearly shows that the brighter region in Fig. 3(a) is Pr enriched.
 | ||
| Fig. 3 (a) STEM-HAADF image, (b) EDX spectrum from a region marked by area 1 in (a). (c) Drift corrected (yellow box) EDX line scan along line 2 in (a). | ||
To identify further the nanocomposite nature of these structures, we have carried out chemical imaging using energy-filtered TEM (EFTEM) technique. The elemental distribution (mapping) obtained using this technique is shown in Fig. 4. Fig. 4(a) shows an unfiltered TEM image. The corresponding zero-loss (elastic) and thickness map is shown in Fig. 4(b) and (c), respectively. Thickness map clearly shows that grains are having different thicknesses. So, Z-contrast image in Fig. 3(a) cannot tell exclusively whether the different regions of nanocomposite are enriched by a particular element having higher or lower Z-element. This is why we have carried out EFTEM imaging using core-loss region of different elements forming this nanocomposite structure. Chemical maps from La M (832 eV), Pr M (931 eV), Mn L (640 eV) and O K (532 eV) edges were obtained using jump-ratio method by acquiring two images (one post-edge and one pre-edge), to extract the background, with an energy slit of 20 eV. The composite image shown in Fig. 4(h) clearly indicates the presence of PCMO–LSMO nanocomposite structures.
The magnetic properties indicate the ferromagnetic nature of the nanostructure compounds. In Fig. 5, we have plotted the magnetization as a function of external magnetic field at T = 5 K. Before starting the measurements, the samples were cooled from T = 380 K in the absence of any external magnetic field. Our measurement indicates the soft ferromagnetic nature of the compounds with very small coercivity (∼50 Oe).
 | ||
| Fig. 5 Magnetization as a function of external magnetic field for LSMO, nanocomposite-1 and nanocomposite-2 at T = 5 K. | ||
Resistivity as a function of temperature in the absence of external magnetic field shows metal insulator type transition near T = 210 K for the nanostructure compounds. The transition shifted towards high temperature when external magnetic field was applied. At a low temperature region, (far below from metal insulator transition) compounds (LSMO, nanocomposite-1 and nanocomposite-2) show an upturn in resistivity with lowering of the temperature. This increasing nature of resistivity at low temperature is suppressed in the presence of an external magnetic field. However, the increasing nature persists even in the presence of a magnetic field of 8 T.
To address the behavior of electrical resistivity in the ferromagnetic metallic region, several attempts have been made.27–30 Jaime et al. proposed that the generally observed dominant contribution of T2 dependence term is caused by the single magnon scattering.27 However, the interpretation by Zhao et al. raised the question about the validity of this model in case of manganites.28 Taking into account the electron–magnon scattering along with the electron–electron interaction, Kubo et al. suggested that the resistivity below metal insulator transition is given by the following equation:30
| ρ(T) = ρ0 + ρ2T2 + ρ4.5T4.5 | (1) |
In this model, the resistivity due to temperature independent scattering process is represented by the term ρ0.31 ρ2T2 indicates the electron–electron interaction and ρ4.5T4.5 includes electron–magnon scattering.29 The model represents our experimental data fairly well. We have fitted the experimental data from T = 200 K to T = 100 K by eqn (1) and using the different coefficients (ρ0, ρ2 and ρ4.5), the data was extrapolated below to T = 5 K. Fig. 6(a) shows the experimental resistivity data of the nanostructures and solid red line in this figure represents the fitting of resistivity data as a function of temperature by using eqn (1) in the absence of an external magnetic field. Similar good fitting was also observed for temperature variation of resistivity data even in the presence of external magnetic field. In this context, it should be mentioned that at the low temperature region, especially below T = 80 K, a deviation between the experimental and calculated resistivity data was observed. Quantitatively, the deviation [δρ = ρ(expt.) − ρ(calculated)] is plotted in the inset of Fig. 6(a). It is well documented that at high temperature region, especially above the metal insulator transition, the electronic transport is governed through small polaron hopping. Mathematical representation of resistivity as a function of temperature is given by
 | (2) |
 | ||
| Fig. 6 (a) Resistivity as a function of temperature in the metallic region for LSMO, nanocomposite-1 and nanocomposite-2 nanostructure in the absence of a magnetic field. Solid red line represents the fitting curve of experimental data by using eqn (1). Inset of (a) represents the deviation between experimental and calculated resistivity. (b) Fit to the resistivity data of nanostructures according to the adiabatic small polaron hopping above metal insulator transition in the absence of external magnetic field. | ||
The fitting of the experimental data for LSMO and nanocomposites for the insulating region by using eqn (2) is given in Fig. 6(b). Activation energy Ea has been calculated from the slope of the fitted line and it was found to be ∼32.6 meV, ∼37.38 meV and ∼36.55 meV for LSMO, nanocomposite-1 and nanocomposite-2, respectively. Another fitting parameter ‘A’ can be calculated by the extrapolation of linear fitted line shown in Fig. 6(b). Calculated value of ‘A’ is 1.21 × 10−4 Ω cm K−1, 1.40 × 10−4 Ω cm K−1 and 3.04 × 10−4 Ω cm K−1 for LSMO, nanocomposite-1 and nanocomposite-2, respectively. According to the Worledge et al., the coefficient ‘A’ is connected with number density of charge carrier.32 The observation of low temperature minima in resistivity is almost a generic behavior of ferromagnetic granular materials.19–22 Numerous models have been proposed to explain this phenomenon. In case of polycrystalline manganites, it is attributed to Coulomb blockade (CB)33 or electron–electron interaction.34 Considering bulk scattering model, which includes quantum correction to conductivity, Rozenberg et al. argued that this model strongly disagrees with the experimental data for ceramic manganites as the resistivity minima is present even in a finite magnetic field.21 However, for strongly field dependent minima of resistivity at low temperature for granular materials, intergranular spin polarized tunneling model (SPT) is proposed.35 According to this model, the depth of the resistivity minima decreases with increase of magnetic field and at a particular field value, it vanishes. The simplified functional form of resistivity at low temperature, considering tunneling through the grain boundary, is given by36
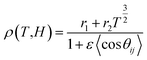 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θij〉 is represented by the following equation:
θij〉 is represented by the following equation:
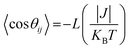 | (4) |
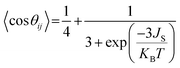 | (5) |
ρ(T) = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(√(Δ/T)) exp(√(Δ/T))
| (6) |
 | ||
| Fig. 7 Temperature dependent resistivity in the absence of an external magnetic field at low temperature region of LSMO nanoparticles are fitted by using several models. | ||
In our present case, upturn in resistivity at low temperature region for all compounds are suppressed but it does not completely vanish even at a 8 T external magnetic field. Therefore, we treat the problem in the light of inter grain tunneling model. Temperature variation of resistivity at low temperature for LSMO and nanocomposite compounds in the absence of magnetic field are fitted by using eqn (3) and (4), whereas eqn (3) and (5) are used to fit the experimental data taken in the presence of an external magnetic field. In both the cases, an excellent fit was observed, which is displayed in Fig. 8.
 | ||
| Fig. 8 (a), (b) and (c) are the electrical resistivity of LSMO nanoparticles, nanocomposite-1 and nanocomposite-2, respectively, at low temperature region in the absence and in the presence of an external magnetic field. Solid line (red line) represents the fitting curve by using eqn (3). | ||
External magnetic field dependence of magnetoresistance (MR) [MR = {R(H) − R(0)}/R(0)] at different temperatures of LSMO and nanocomposites is displayed in Fig. 9.
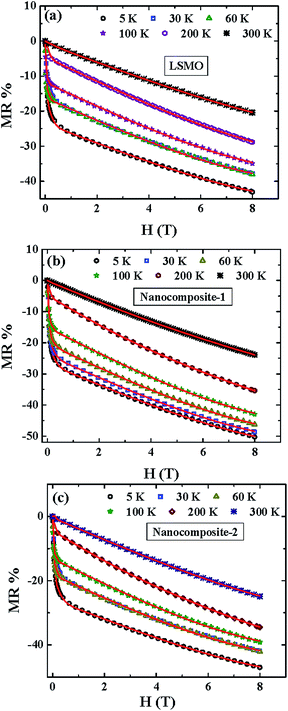 | ||
| Fig. 9 Magnetoresistance (MR) as a function of magnetic field for (a) LSMO and (b) nanocomposites. Solid red line represents the fitted data using eqn (7). | ||
Sharp increasing nature of the magnitude of MR at low magnetic field was observed in both the cases, which is analogous to the typical ferromagnetic granular materials at low temperature. This sharp drop of MR can be explained by taking into account the intergranular spin polarized tunneling. According to Hwang et al., the movement of magnetic domain walls through the grain boundaries due to the application of an external magnetic field is associated with the progressive alignment of magnetic domains and as a result, a sharp drop of MR at low field was observed.18 In addition, MR slightly increases in the case of nanocomposites compared to LSMO. From the magneto-transport measurements (resistance as a function of external magnetic field, R(H)), we calculated MR by using the abovementioned expression. The numerical values of the resistance at T = 30 K and 60 K (at low field region) are very close to each other for LSMO and nanocomposite-2 compound, respectively. However, R(H) at T = 30 K and 60 K shows an almost parallel nature at the high magnetic field region. As a result, the quantitative values of MR (at T = 30 K and 60 K) overlapped and they maintained a small difference in the low field region for the nanostructured LSMO and nanocomposite-2.
To explore the main role behind this enhancement of MR in nanocomposite type nanostructures, our primary objective is to separate the different contributions of MR, originating from SPT (MRSPT) and from the suppression of spin fluctuation owing to the applied magnetic field (MRINT). Considering the response of gradual slippage of domain walls across the grain boundaries as pinning centers, Raychaudhuri et al. proposed a phenomenological model for MR based on SPT.40 According to this model, expression of MR is as follows:
 | (7) |
f(K) = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−BK2) + CK2 exp(−BK2) + CK2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−DK2) exp(−DK2)
| (8) |
By using the value of the fitting parameters A, B, C, D, J and K (because à is absorbed in A and C), one can separate out MRSPT and MRINT parts from total MR in the following manner:
 | (9) |
| MRINT = −JH − KH3 | (10) |
To fit the MR data of the nanostructure compounds, we have followed the same procedure as that considered by Raychaudhuri et al.40 According to their model, the derivative of the MR as a function of the external magnetic field is given by the following equation:
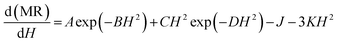 | (11) |
By differentiating our experimental MR data with respect to H, we have fitted the d(MR)/dH as a function of H curve using eqn (11) and extracted the best fitting parameters for different temperatures. Using these best fitting parameters, we have calculated MR as a function of H from eqn (7). The variation of MR with an external magnetic field along with the fitted line for LSMO and nanocomposites are shown in Fig. 8.
By using the best fitted parameters at different temperature, we have calculated temperature dependence of MRSPT and MRINT for both compounds from eqn (9) and (10), respectively. The variation of MRSPT and MRINT is plotted in Fig. 10(a) and (b), respectively.
 | ||
| Fig. 10 (a) Temperature dependence of MRSPT for LSMO and nanocomposites at H = 10 kOe magnetic field. (b) Temperature variation of MRINT for those compounds at the same magnetic field of H = 10 kOe. | ||
From Fig. 10(a), it is clear that MRSPT is enhanced in nanocomposites compared to LSMO nanoparticles. This interesting behavior of nanocomposites can be explained considering the effect of extra grain boundaries of PCMO in LSMO matrix compared to LSMO nanoparticles. It is also reported that MRSPT is very sensitive with the behavior of the grain boundaries. Dey et al. studied the magneto-transport properties of La0.7Ca0.3MnO3 nanoparticles (down to 17 nm). They observed that MRSPT increases and it is almost constant with decreasing particle size (i.e. enhanced grain boundaries effect) across a wider temperature range.39 We examined the low and high field magnetoconductivity data of our compounds. To elucidate this, we have adopted the model proposed by Lee et al.25 According to their model, magnetoconductivity (σ) as a function of magnetic field is given by the simplified relation
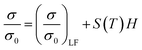 | (12) |
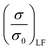 term corresponds to the low field magnetoconductance, which depends on the different magnetization orientation of neighboring grains, whereas the term S(T)H is connected with the magnetic behavior of the grain boundaries.
term corresponds to the low field magnetoconductance, which depends on the different magnetization orientation of neighboring grains, whereas the term S(T)H is connected with the magnetic behavior of the grain boundaries.
By fitting our experimental magnetoconductivity as a function of magnetic field data at the high field region using eqn (12), we have extracted the surface spin susceptibility ‘S’ at different temperatures. One typical linear fitting of magnetoconductance as a function of magnetic field for LSMO and nanocomposite at T = 5 K is shown in Fig. 11(a). It is worth noting that the observed low field magnetoconductance of nanocomposite is very close to universal limit through second order tunneling.25 The temperature dependence of surface spin susceptibility ‘S’ of LSMO and nanocomposites are presented in Fig. 11(b). Very interestingly, we found that the nature of the S(T) is qualitatively similar to that of MRSPT(T). Quantitatively, we also found that surface spin susceptibility increases in our nanocomposites similar to MRSPT. The comparative analysis of our transport and magnetotransport data indicates that the behavior of MR is decided predominantly by the nature of the response of surface magnetization of these nanosized magnetic particles, as suggested by Lee et al.25
From the magnetic and magneto-transport measurements, we observe that the charge ordered-ferromagnetic nanocomposites shows qualitatively same behavior as LSMO. However, due to the effect of the artificial grain boundaries in nanocomposite nanostructures, the responses differ quantitatively with respect to its parent ferromagnetic LSMO nanoparticles. It is worth mentioning that the nanocomposite compounds also quantitatively modify their properties, depending upon sintering temperatures, which are mentioned in the sample preparation part.
4. Concluding remarks
To summarize, we have synthesized PCMO–LSMO nanocomposites as well as LSMO nanoparticles by the sol–gel route. The effect of the artificial grain boundaries on transport and magnetotransport properties of the prepared charge ordered-ferromagnetic nanocomposites has been investigated. Low temperature upturn in resistivity for all the compounds is well described by spin polarized tunneling model. Enhanced magnetoresistance and low field magnetoconductance in case of the nanocomposites compared to the LSMO nanoparticles are analyzed considering the second order tunneling mechanism through the grain boundaries. Our study indicates that the spin polarized tunneling in these kind of compounds plays a dominant role for the rise in resistivity with lowering temperature in low temperature region and also for the low field magnetoresistance.Acknowledgements
One of the authors, Kalipada Das, would like to sincerely acknowledge CSIR-INDIA for the fellowship. We thank Pallab Bag and R. Rawat, UGC-DAE Cosortium for Scientific Research, Indore, for magnetoresistance measurements and Sudipta Mondal, SINP, Kolkata, for help in X-ray data analysis.References
- Y. Tokura, Colossal Magnetoresistive Oxides, Gordon and Breach Science, Amsterdam, 2000 Search PubMed.
- H. Kuwahara, Y. Tomioka, A. Asamitsu, Y. Moriotomo and Y. Tokura, Science, 1995, 270, 961 CAS.
- A. Biswas, I. Das and C. Majumdar, J. Appl. Phys., 2005, 98, 124310 CrossRef PubMed.
- A. Biswas and I. Das, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 172405 CrossRef.
- A. Biswas, T. Samanta, S. Banerjee and I. Das, Appl. Phys. Lett., 2009, 94, 233109 CrossRef PubMed.
- J. Ding, Z. Lin, J. Wu, Z. Dong and T. Wu, Small, 2015, 11, 576 CrossRef CAS PubMed.
- A. Biswas and I. Das, Appl. Phys. Lett., 2008, 92, 012502 CrossRef PubMed.
- M. Uehara, S. Mori, C. H. Chen and S. W. Cheong, Nature, 1999, 399, 560 CrossRef CAS PubMed.
- L. Zhang, C. Israel, A. Biswas, R. L. Greene and A. de Lozanne, Science, 2002, 298, 805 CrossRef CAS PubMed.
- S. Dong, R. Yu, S. Yunoki, J. M. Liu and E. Dagotto, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 064414 CrossRef.
- H. Y. Hwang, S. W. Cheong, P. G. Radaelli, M. Marezio and B. Batlogg, Phys. Rev. Lett., 1995, 75, 914 CrossRef CAS.
- P. Lyu and D. Y. Xing, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 54 CrossRef CAS.
- M. Viret, M. Drouet, J. Nassar, J. P. Contour, C. Fermon and A. Fert, Europhys. Lett., 1997, 39, 545 CrossRef CAS.
- L. I. Balcells, J. Fontcuberta, B. Martnez and X. Obradors, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, R14697 CrossRef CAS.
- R. Shreekala, M. Rajeswari, K. Ghosh, A. Goyal, J. Y. Gu, C. Kwon, Z. Trajanovic, T. Boettcher, R. L. Greene, R. Ramesh and T. Venkatesan, Appl. Phys. Lett., 1997, 71, 282 CrossRef CAS PubMed.
- A. de Andres, M. Garca-Hernandez and J. L. Martnez, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 7328 CrossRef CAS.
- P. Wagner, I. Gordon, L. Trappeniers, J. Vanacken, F. Herlach, V. V. Moshchalkov and Y. Bruynseraede, Phys. Rev. Lett., 1998, 81, 3980 CrossRef CAS.
- H. Y. Hwang, S. W. Cheong, N. P. Ong and B. Batlogg, Phys. Rev. Lett., 1996, 77, 2041 CrossRef CAS.
- S. Das and T. K. Dey, Solid State Commun., 2005, 134, 837 CrossRef CAS PubMed.
- S. Das and T. K. Dey, J. Magn. Magn. Mater., 2005, 294, 338 CrossRef CAS PubMed.
- E. Rozenberg, M. Auslender, I. Felner and G. Gorodetsky, J. Appl. Phys., 2000, 88, 2578 CrossRef CAS PubMed.
- S. Mukhopadhyay and I. Das, Europhys. Lett., 2007, 79, 67002 CrossRef.
- L. Balcells, L. Abad, H. Rojas, A. P. del Pino, S. Estrade, J. Arbiol, F. Peiro and B. Martinez, Small, 2008, 4, 365 CrossRef CAS PubMed.
- Y. Wang and H. J. Fan, Small, 2012, 8, 1060 CrossRef CAS PubMed.
- S. Lee, H. Y. Hwang, B. I. Shraiman, W. D. Ratcliff and S. W. Cheong, Phys. Rev. Lett., 1999, 82, 4508 CrossRef CAS.
- P. G. Radaelli, et al., Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 8265 CrossRef CAS.
- M. Jaime, P. Lin, M. B. Salamon and P. D. Han, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, R5901 CrossRef CAS.
- G. Zhao, V. Smolyaninova, W. Prellier and H. Keller, Phys. Rev. Lett., 2000, 84, 6086 CrossRef CAS.
- G. Jeffrey Snyder, R. Hikes, S. DiCarolis, M. R. Beasley and T. H. Geballe, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 14434 CrossRef.
- K. Kubo and N. A. Ohata, J. Phys. Soc. Jpn., 1972, 33, 21 CrossRef CAS.
- A. S. Alexandrov and A. M. Bratkovsky, Phys. Rev. Lett., 1999, 82, 141 CrossRef CAS.
- D. C. Worledge, G. Jeffrey Snyder, M. R. Beasley, T. H. Geballe, R. Hiskes and S. DiCarolis, J. Appl. Phys., 1996, 80, 5158 CrossRef CAS PubMed.
- M. Garcia-Hermandez, F. Guinea, A. de Andres, J. L. Martinez, C. Prieto and L. Vazquez, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 9549 CrossRef.
- A. Tiwari and K. P. Rajeev, Solid State Commun., 1999, 111, 33 CrossRef CAS.
- J. S. Helman and B. Abeles, Phys. Rev. Lett., 1976, 37, 1429 CrossRef CAS.
- M. I. Auslender, E. Rozenberg, A. E. Karlin, B. K. Chaudhuri and G. Gorodetsky, J. Alloys Compd., 2001, 326, 81 CrossRef CAS.
- O. Ciftja, M. Luban, M. Auslender and J. H. Luscombe, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 10122 CrossRef CAS.
- P. Sheng, B. Abeles and Y. Arie, Phys. Rev. Lett., 1973, 31, 44 CrossRef CAS.
- P. Dey and T. K. Nath, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 214425 CrossRef.
- P. Raychaudhuri, K. Sheshadri, P. Taneja, S. Bandyopadhyay, P. Ayyub, A. K. Nigam and R. Pinto, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 13919 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2015 |




