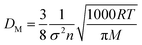DOI:
10.1039/C5RA00085H
(Paper)
RSC Adv., 2015,
5, 48442-48455
Performance of silicon rubber coated polyetherimide hollow fibers for CO2 removal via a membrane contactor
Received
3rd January 2015
, Accepted 7th May 2015
First published on 11th May 2015
Abstract
This study focuses on the effect of a silicon rubber coating technique on the hollow fiber membrane contactor for the purpose of CO2 removal. The polymer and the coating agent used were polyetherimide (PEI) and polydimethylsiloxane (PDMS) respectively. The hollow fibers were fabricated via a simple wet spinning technique. The surfaces of the hollow fibers were coated by means of PDMS dissolved in n-hexane applying different protocols. An effort was made to keep the silicon rubber coating layer porous. The membranes were characterized by applying a gas permeation test (GPT) via pure helium, critical entry pressure of water (CEPw), contact angle, a gas absorption test and scanning electron microscopy (SEM). Based on the observations, the coating technique resulted in drastic changes in the contact angle and CEPw of the coated membranes for the inside and outside coated hollow fiber membranes. Disregarding the method of coating and even the polymer concentration, the contact angle was enhanced dramatically. The CO2 absorption results revealed that by blowing nitrogen (600 kPa) through the lumen side of the hollow fibers during the PDMS coating process onto the outside surface, the absorption flux of the membranes was increased. A slight decrease in the CO2 absorption flux for the other cases was outweighed by a substantial enhancement in the membrane wetting resistance due to the high contact angle and CEPw. These observations showed the high influence of the silicon rubber layer on the CO2 gas absorption, which emphasizes the role of this key-parameter in controlling the ultimate membrane contactor performance.
1. Introduction
Aggressive levels of anthropogenic greenhouse gases, primarily carbon dioxide (CO2), impose irreversible environmental, economic and operational impacts on the Earth. Hence, controlling the CO2 content in gas streams and its emission to the atmosphere is essential. Practical techniques of capturing CO2 through direct contact in the gas/liquid state with physical or chemical absorption processes are widespread and best exemplified by packed towers, tray towers and bubble columns. However, these methods possess weaknesses such as low contact area, tremendous energy consumption, and may result in operational drawbacks such as weeping, foaming and flooding. The higher efficiency offered by membrane contactors for CO2 removal and their beneficial advantages, in terms of capital investments, operational costs and energy savings due to the miniaturization of the conventional processes, have gained attention for this process.1,2 Membrane contactors are regarded to be better than conventional dispersed phase contactors because they possess no flooding at high flow rates, no unloading at low flow rates, the absence of emulsions, and no requirement for a density difference between the two fluids contacted.3 They reduce the volume of the equipment and offer a bigger interfacial area in non-dispersive contact across a membrane, leading to the decrease of the HTU (height of a transfer unit) values, hence achieving a higher value of the mass transfer coefficient.4 To fully exploit the growing opportunities in the field of membrane contactor processes, precedence has been given to the identification of new membrane materials that comply with the current requirements. The criteria for selecting membrane materials for a given separation process are complex, and they include durability, mechanical integrity at operating conditions, high transmembrane flux and hydrophobicity.
The transport of gas in a membrane contactor is based on a diffusion mechanism that allows the gas to flow from one end of the pore in contact with the gas to the gas/liquid interface at the other end of the pore. The separation performance for this process is determined by the distribution coefficient of a component in two phases, with the membrane acting only as an interface.5 Therefore, the membrane must possess high hydrophobicity with a small pore size to prevent wetting and high permeability to increase the diffusion rate.6 Hence, there is a need to carefully choose the membrane materials to prepare membranes with an improved structure to fulfill the requirements of the gas/liquid contact processes. Regardless of the above advantages, a clear drawback of the membrane contactors is the presence of the membrane barrier between the two phases separated by the membrane, which introduces an extra resistance to the overall mass transfer process. Therefore, the membrane applied should possess a high bulk porosity to minimize the fraction of the membrane resistance. Unfortunately, a membrane with a high bulk porosity may lead to a membrane with a higher wetting affinity. Therefore, its use is limited due to membrane wetting problems in the operation step, longevity and its high membrane cost. Complete or even partial wetting of the membrane pores by the liquid results in a dramatic decrease in the mass transfer flux due to an excess resistance produced by the stagnant liquid phase trapped inside the pores.7 Hence, in order to employ an efficient membrane contactor, the membrane wetting phenomena must be prevented.8,9
Essentially, there are three categories of techniques to overcome membrane wetting, and hence improve the process performance, namely by surface modification (to increase the surface hydrophobicity), tuning the membrane structural parameters (pore size distribution and membrane porosity) and the operating conditions. Various physical and chemical techniques have been performed for membrane surface modification including coating, grafting, plasma polymerization, etc.10 Among these techniques, the surface modification by applying a coating of hydrophobic materials is the main concern of the current work, to eliminate membrane wetting in hollow fiber membrane contactors. However, a dense layer of the coating material will introduce an additional resistance to the mass transfer which will inevitably lead to a reduction of the mass transfer rate i.e. the transmembrane flux of the membrane. The reduction of the mass transfer rate due to the membrane resistance has been stated to be compensated by an elevation of the feed gas pressure, i.e., by increasing the driving force.11
Kreulen et al.12 performed a series of experiments to absorb CO2 and N2O via MC. Different polypropylene (PP) hollow fibers, including silicon rubber coated hollow fibers, were utilized. They concluded that no significant mass transfer reduction occurred after adding a silicone layer. In 1994, Papadopoulos and Sirkar prepared a hollow fiber membrane contactor by using a thin nonporous silicone layer to handle higher gas pressures. It was reported that the aqueous 20% diethanol amine (DEA) led to a substantially higher overall CO2 permeability and selectivity.13 Bessarabov et al. fabricated flat sheet polymeric composite membranes for CO2 separation to operate as a bubble free process. However, they did not report any comparison between coated and uncoated membrane flat sheets.14 Nymeijer et al. reported the results of PP/ethylene propylene diene terpolymer (EPDM) (1 wt% in n-hexane) coated hollow fibers for the separation of an ethane–ethylene mixture. They showed that the membrane performance remained constant for more than 20 weeks. However, the comparison of the absorption flux of the coated membranes with the neat membranes was not reported.15 In 2006, Kneifel et al. investigated the performance of polyetherimide hollow fiber membranes coated with a thin dense layer of polydimethylsiloxane (PDMS) with respect to the water vapor permeance to control air humidity. It was shown that the negative effect of the coating on the permeance could be restricted to a permeance loss of about 20% by applying a very thin coating layer.16 Jin et al. spun hollow fibers from materials made of poly(phthalazinone ether sulfone ketone) (PPESK). The membrane surface was then modified by a coating layer of hydrophobic PDMS and sol–gel polytrifluoropropylsiloxane. The stability of the membranes was evaluated by long-term experiments. Unfortunately, they did not report any comparison between the neat and the coated HF membranes.17 Nguyen et al. reported research on fabricating composite membranes for CO2 separation via monoethanol amine. The composite membrane comprised of polypropylene as the support layer and poly(1-(trimethylsilyl)-1-propyne) (PTMSP) or Teflon AF2400 as the dense top layer. They concluded that a dense skin, when carefully selected and coated, can provide protection from not only the wetting effect to the support but also towards chemical and thermal degradation.18 A brief review of hollow fiber coatings in the application of membrane contactors is shown in Table 1.
Table 1 A brief review of the coating of hollow fiber membranes for gas/liquid contactorsa
| Researcher |
Polymer |
Membrane config. |
Coating layer |
Coated layer structure |
Absorbent |
Application |
Ref. |
| All of the abbreviations are defined in the text. |
| Kreulen et al. (1993) |
PP |
Hollow fiber |
PDMS |
Dense |
Sodium hydroxide |
CO2 and N2O |
12 |
| Papadopoulos and Sirkar (1994) |
PP |
Hollow fiber |
PDMS |
Dense |
Water and DEA |
CO2/N2 |
13 |
| Bessarabov et al. (1996) |
PDMS |
Dense flat sheet |
— |
Dense |
Water |
CO2 |
14 |
| Nymeijer et al. (2004) |
PP Accurel® |
Hollow fiber |
EPDM |
Dense |
AgNO3 solutions |
C2H6/C2H4 |
15 |
| Kneifel et al. (2006) |
PEI |
Hollow fiber |
PDMS |
Dense |
Water |
Air humidity |
16 |
| Jin et al. (2008) |
PPESK |
Hollow fiber |
PDMS |
Dense |
Water |
Water vapour |
17 |
| Nguyen et al. (2011) |
PP Oxyphan® |
Hollow fiber |
PTMSP or Teflon AF2400 |
Dense |
MEA |
CO2 |
18 |
As shown in the table, currently none of the works have investigated the effect of a silicon rubber coating on a porous support when the resulting pores are still kept open after the coating. Therefore, the scope of this work is coating the surface of polyetherimide hollow fiber membranes by applying PDMS while keeping the membrane pores open, and investigating the effects of various parameters such as PDMS concentration and the procedures of different protocols of coating on the structural parameters of the membranes along with the performance for the gas absorption process.
2. Theoretical framework
A vast number of researchers have devoted their interests to the partial wetting of hollow fibers in the membrane contactor process.19–22 Fig. 1 demonstrates the different gas/liquid contact configurations and the concentration gradient of CO2 in the bulk and boundary layer of the gas phase, the membrane’s structure and the bulk and boundary layer of liquid phase, including: (a) a partially wetted porous membrane contactor, (b) a fully dry porous membrane contactor, (c) a porous membrane contactor possessing a dense hydrophobic skin layer, and (d) a porous membrane contactor possessing a porous hydrophobic skin layer. In all the above cases, the gas stream is assumed to be a pure gas, e.g. CO2. In addition, in all the cases, CO2 is finally dissolved in an aqueous solution i.e. water, which is carried out by the solution stream. The controlling parameter is equated to the rate of CO2 diffusion in the pores. When the pores are gas-filled, CO2 molecules diffuse in the gas phase, whereas when the pores are partially or totally liquid-filled, CO2 molecules inevitably diffuse in the liquid phase. Generally, the diffusion coefficients of gas molecules in a gaseous phase relative to a liquid phase are substantially higher by a factor of 104–105. Therefore the gas absorption flux is controlled by the extent of pore wetting. Case ‘a’ shows a membrane which is partially wetted. Here, the absorbent solution can penetrate into the membrane gas-filled pores, resulting in a substantial increase of the mass transfer resistance against CO2 pore diffusion. Case ‘b’ illustrates an ideal membrane which possesses fully liquid-untouched pores. There is no barrier except the gas diffusion through the pores, and hence its absorption performance is the highest among all of the considered cases.19,20 In case ‘c’, a nonporous dense hydrophobic coating layer is fully applied onto the skin layer of the support membrane. It is clear that no solution can pass through the coated layer and penetrate into the pores. Hence, we obtain a fully dry system. However, an extra resistance due to the dense coated layer is introduced to the system’s overall mass transfer resistance. Finally, we have the case ‘d’, which is the scope of the present work. This case demonstrates a membrane possessing a hydrophobic porous layer coated on top of the support layer. In contrast to case ‘c’, ideally no extra mass transfer resistance due to the coating layer will be added to the system. Consequently, case ‘d’ also includes the hydrophobic character of case ‘c’, which protects the membrane pores against wetting. This in turn exhibits the gas-filled pore character of case ‘b’ as well. It is noted that, the thickness of the coating layer is practically negligible with respect to the membrane thickness. However, the coating may lead to a change in the surface porosity or the mean pore size, which will be discussed in more detail shortly.
 |
| | Fig. 1 A schematic diagram of different concentration gradients of CO2 in the bulk and boundary layers of the gas and liquid phases, and the membrane’s structure, for (a) a partially wet porous membrane contactor, (b) a fully dry porous membrane contactor, (c) a porous membrane contactor possessing a dense hydrophobic skin layer, and (d) a porous membrane contactor possessing a porous hydrophobic skin layer (GB: gas bulk, GBL: gas boundary layer, LB: liquid bulk, and LBL: liquid boundary layer; the colors represent the following media; yellow: gas stream, blue: liquid stream, gray: porous membrane cross section and black: coating layer). | |
Considering Fig. 1, the most number of similarities can be found between case ‘b’ and case ‘d’. It is obvious that cases ‘b’ and ‘d’ display the least membrane mass transfer resistance. This was shown experimentally by Nguyen et al.9 Nevertheless, in case ‘d’, depending on the coating procedure, some of the pores might have been partially blocked during the coating step. As a result, the mass transfer resistance could be slightly to strongly higher than case ‘b’. Because of this, in the current work, experiments were conducted in the attempt to materialize this concept.
3. Experimental
3.1. Raw materials
The membranes were prepared from commercial Ultem® 1000 polyetherimide (PEI) supplied by GE plastic USA. N-Methyl-2-pyrrolidone (NMP), used as a solvent, was supplied by Merck. A rubbery silicone polymer (Sylgard 184), supplied by Dow Corning USA, was used as the coating agent. PEI pellets were preconditioned in a vacuum oven at 80 °C for 72 h to remove trapped moisture. All materials were used as received.
3.2. Dope preparation
To prepare the casting solution, the polymer was divided into three portions which were added to the solvent consecutively with a time interval of 15 min. The polymer (12 or 15 wt%)–solvent mixture was then stirred for 18 h at 60 °C to ensure complete dissolution of the polymer. The solution was further degassed under ultrasonication for 2 h and was left overnight before performing the spinning process.
3.3. Asymmetric polyetherimide hollow fiber membrane preparation
A wet spinning technique, without any air gaps, was employed in fabricating the asymmetric PEI hollow fiber membrane for this study.
The spinneret used for spinning had a dimension of 1.25 mm for the outer diameter (OD) and 0.55 mm for the inner diameter (ID). The polymer dope was sent to the spinneret with a constant flow rate of 4.0 cm3 min−1 at room temperature (∼23 °C) applying a syringe pump to pressurize the polymer dope to pass the spinneret. Another syringe pump was used to deliver the bore fluid (distilled water) with a constant flow rate of 1.7 cm3 min−1. Tap water, with a temperature of ∼23 °C, was used for the external coagulant. After completing the spinning, to ensure that all of the solvent in the membrane structure was removed, the membranes were immersed in water for 3 days, with a daily change of water to remove the residual solvent, followed by drying for 3 to 4 days at room temperature. The OD/ID of the prepared hollow fibers were 0.67/0.41 mm and 0.73/0.44 mm for PEI-12 wt% and PEI-15 wt% respectively.
3.4. Membrane coating
The hollow fiber membranes were coated via a rubbery silicone polymer (Dow Corning Sylgard 184). The intention of the coating was to modify the external or the internal surface of the membranes from a hydrophilic surface to a hydrophobic surface. The membranes were submerged into a 0.5% w/w solution of silicone rubber in n-hexane for 1 to 2 s under nitrogen blowing conditions through the membranes lumen side. In order to perform the coating onto the inner surface, the silicon rubber solution (0.1%, 0.2% and 0.5% w/w solution) was fed into the lumen of the fibers, and then the solution was discharged by applying a nitrogen gas stream. The thickness of the silicone layer was varied as a function of the concentration of the coating solution. The coated membranes were subsequently placed in an oven at ∼60 °C for 24 hours to ensure the curing of the coating layer before performing the gas permeation testing (GPT) and contactor performance testing. The code and specifications of the fabricated membranes are summarized in Table 2.
Table 2 Code and specifications of the fabricated membranes before and after coating
| Membrane code |
PEI concentration wt% |
Silicon rubber wt% |
Coated surface |
Remark |
| M-15 |
15 |
— |
— |
Uncoated |
| M-15-0.5-WB |
15 |
0.5 |
Outside |
Without N2-blowing |
| M-15-0.5-600B |
15 |
0.5 |
Outside |
600 kPa N2-blowing |
| M-15-0.5-IC |
15 |
0.5 |
Inside |
N2-blowing |
| M-12 |
12 |
— |
— |
Uncoated |
| M-12-0.1-IC |
12 |
0.1 |
Inside |
N2-blowing |
| M-12-0.2-IC |
12 |
0.2 |
Inside |
N2-blowing |
| M-12-0.5-IC |
12 |
0.5 |
Inside |
N2-blowing |
3.5. Gas permeation test
Two to three hollow fibres were glued with epoxy resin at one end and the other end was potted to a stainless steel fitting inserted into a stainless steel cylinder. The GPT system is shown schematically in Fig. 2. The feed gas (He 99.97 vol%) was supplied to the lumen side of the membranes and the pressure was controlled by a pressure regulator. The rate of gas permeation was measured using a constant-pressure method. For measuring the permeation rate a soap bubble flow meter was utilized. The permeation tests were carried out at 23 °C and the feed side pressure was varied from 25 kPa to 350 kPa gauge depend on the permeation rate of the membranes. The permeance was calculated as follows:| |
 | (1) |
where P is the gas permeance (mol m−2 Pa−1 s−1), R is the universal gas constant (8.314 J mol−1 K−1), T is the system absolute temperature (K), V is the volume of gas permeated through the membrane (m3, STP), A is the effective membrane area (m2), t is the permeation time (s) and Δp is the transmembrane pressure drop (Pa). It is noted that the constant 101![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 325 is the absolute atmospheric pressure of the permeate side in Pa.
325 is the absolute atmospheric pressure of the permeate side in Pa.
 |
| | Fig. 2 Gas permeation testing rig. | |
3.6. Measurement of critical entry pressure of water and contact angle
The critical entry pressure of water (CEPw) test is to measure the minimum pressure required to let water penetrate through the membrane pores and is used as an indication of wettability resistance of the membrane. Distilled water was pressurised into the lumen side of the dried hollow fibre membrane and the pressure was increased gradually at a step size of 50 kPa gauge. The pressure at which the first droplet of water appeared on the outer surface of the membrane was recorded as the CEPw, which is the minimum pressure required to drive water through the largest membrane pores.
Water contact angle measurement is a simple way to quantify the hydrophilicity/hydrophobicity characteristic of the membrane’s surface. The contact angle of the outer and inner surfaces of the membranes were measured by a contact angle meter (model OCA20, Dataphysics, Germany) and distilled water was used as the probe liquid. The contact angle was recorded immediately after putting a tiny droplet of water on the membranes. At least 10 points were used for the contact angle measurement and the average values were reported.
3.7. Gas absorption test
To evaluate the performance of the silicon rubber coated membranes, the fibres were assembled in a membrane contactor module and CO2 absorption tests were conducted. The following two cases were considered: running pure CO2 in the shell side and distilled water in the lumen side and conversely, pure CO2 in the lumen side and distilled water in the shell side. Eight PEI hollow fibre membranes were assembled in a contactor module with an inner diameter of 1.57 cm. The effective length of the fibres in the module was 18 cm. The membrane gas absorption rig is shown schematically in Fig. 3. A diaphragm pump was used to flow distilled water at a constant pressure. The liquid pressure was adjusted so that it was 50 kPa higher than the pressure of the CO2 gas to prevent undesired bubbling. Through all of the experiments, the gas flow rate was set constant at 1.0 dm3 min−1. The collected sample of the absorbed CO2 in water was immediately titrated by a solution of 0.05 M NaOH, where phenolphthalein was applied as the equivalent point indicator.23
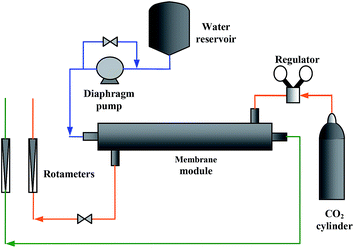 |
| | Fig. 3 Gas absorption rig (orange: CO2, blue: distilled water and green: CO2 solution). | |
Referring to Appendix A, the concentration of [H+] can be evaluated and finally calculate the pH of the system. Accordingly, the maximum CO2 captured by pure water at atmospheric pressure and room temperature provides a pH of almost 5.65. It is noted, the measured pH occurred between ∼5.5 and ∼6.8, as was reported by others.24
The experimental flux can be calculated by a simple mass balance of CO2 over the entire effective length of the membrane module:
| |
 | (2) |
where
QL is the liquid volumetric flow rate (m
3 s
−1),
J is the gas absorption flux (mol m
−2 s
−1),
CoutL and
CinL are the concentrations of CO
2 in the outlet and inlet solutions (mol m
−3) respectively, depending on the lumen or shell side liquid flow,
d is the inside or outside fiber diameter (m),
n is the number of hollow fibers and
L is the length of the fibers (m). Also, the theoretical flux can be obtained by:
where
KOL is the overall mass transfer coefficient (m s
−1) based on the liquid phase and (Δ
Clm) is a log-mean concentration difference of CO
2 between the input and output of the CO
2 solution. Equating
eqn (2) and
(3), one can calculate the overall mass transfer coefficient:
25| |
 | (4) |
and (Δ
Clm) is defined as:
25| |
 | (5) |
where
Cout,iL,
Cin,iL are the concentrations of CO
2 in liquids which are in equilibrium with pure CO
2 at the liquid/gas interface in the outlet and inlet solutions (mol m
−3) respectively. Considering the establishment of the equilibrium condition, the concentration of CO
2 at the liquid/gas interface can be estimated by Henry’s law given by
eqn (6):
where
CiG is the concentration of CO
2 at the liquid/gas interface for the gas phase (mol m
−3) and
H is a dimensionless temperature-dependent Henry constant which is obtained by
eqn (7).
26| |
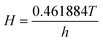 | (7) |
and
h is a Henry constant with the dimension of pressure (MPa) for CO
2 dissolved in water, as computed by:
26| |
 | (8) |
It is noted that since the gas phase is pure CO2, as a result, in the gas phase the interface concentration of CO2 is equal to the bulk concentration of CO2.
3.8. Overall and membrane mass transfer coefficients, resistance-in-series model
The mass transfer coefficient of the liquid boundary layer for the lumen side is mainly determined by the system geometry and flow conditions, for which many correlations are available to predict it.27,28 An approximate solution for the differential equation driven from the continuity equation was proposed by Graetz. For more details please refer to Appendix B.29 In membrane contactor systems, the Wilson plot is widely applied to determine the membrane mass transfer. The mass transfer resistance of the liquid side is proportional to the liquid velocity as v−α, where α is an empirical parameter and v is the liquid velocity. A plot of 1/KOL versus v−α results in a straight line, which is known as a Wilson plot. Then the membrane mass transfer resistance can be calculated from the intercept of the plot. It is believed that this method is more accurate than the predictions achieved by the traditional correlations for the Sherwood number, therefore this method was applied throughout the current study.
According to the resistance-in-series model (eqn (9)), the overall mass transfer resistance consists of three major resistances: gas boundary layer, liquid boundary layer and membrane mass transfer resistances.
| |
 | (9) |
where
KOL,
kL,
kG and
kM are the overall liquid, liquid boundary layer, gas boundary layer and membrane mass transfer coefficients (m s
−1) and
di,
do and
dlm are the hollow fiber inside, outside and log mean diameters (m). In particular, the membrane mass transfer resistance can be written as:
| |
 | (10) |
(It should be noted that
eqn (9) and
(10) are given for the case when the liquid flows in the lumen. When the liquid flows on the shell side the subscript i and o should be exchanged.)
When the gas side is a single component, which here is the present case, the resistance in the gas boundary layer can be neglected.
On the other hand, assuming the membrane pores are gas filled and the mass transfer in the pore is entirely by diffusion without convection, the membrane mass transfer coefficient is given by:
| |
 | (11) |
where
τ is the tortuosity of the skin layer, which can be roughly considered as unity due to the tiny thickness of the skin layer.
DG (m
2 s
−1) is the diffusion coefficient of gas. Further assuming that the diffusion is primarily contributed by Knudsen and molecular diffusion,
DG is given by:
33| |
 | (12) |
For more information on how to estimate the Knudsen and molecular diffusion coefficients the readers can refer to Appendix B.
3.9. Scanning electron microscopy (SEM)
Scanning electron microscopy (SEM, Hitachi, TM-3000) was used to study the morphology of the membranes produced. The hollow fibers were broken in liquid nitrogen carefully to make a smooth surface. The fractured fibers were placed on a disc for sputtering with a thin film of platinum. Then, they were mounted on a stainless steel stand with carbon tape. The SEM micrographs of the cross-section of the hollow fibers were taken at various magnifications.
4. Results and discussion
4.1. Gas permeation results
Fig. 4 illustrates the helium permeance of neat and inside coated hollow fiber membranes. According to the figure, the silicon rubber coating reduced the permeance of the helium gas. Nonetheless, among the PDMS coated membranes, as the silicone rubber concentration increased, the permeance increased as well. Thus, membrane M-12-0.1-IC had the lowest gas permeance while membrane M-12-0.5-IC displayed the highest.
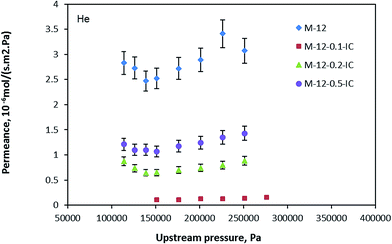 |
| | Fig. 4 Helium permeance of neat and inside silicon rubber coated PEI-12 wt% hollow fiber membranes. | |
Fig. 5 shows the permeance of helium for neat and outside coated hollow fiber membranes. The permeance decreased dramatically by an order of magnitude when the silicone rubber coating was applied without N2 blowing. When N2 gas was blown from the lumen side, the permeance increased dramatically and even surpassed that of the neat hollow fiber. The decrease in the permeance was most probably due to the blockage of the small pores, which resulted in shifting the mean pore size larger and a sharp decrease in the effective porosity. On the other hand, when the N2 gas pressure was applied on the lumen side, the pores were kept open during the coating process, maintaining or even enlarging the pore size and the surface porosity enhanced as a result of the applied gas pressure. Consequently, an increase in the gas permeance as well as an enhancement in the gas absorption flux was expected. Interestingly, membrane M-15-0.5-IC demonstrated the same behavior as membrane M-15-0.5-WB. According to this observation, it was concluded that the effect of inside and outside coating is meaningfully the same, which seems to be reasonable.
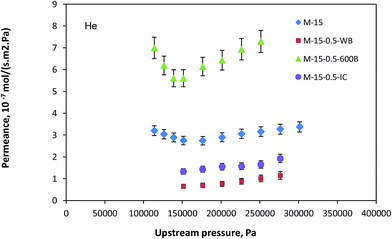 |
| | Fig. 5 Helium permeance of neat and outside silicon rubber coated PEI-15 wt% hollow fiber membranes. | |
Table 3 summarizes the structural parameters of the silicon rubber coated hollow fiber membranes in comparison to the uncoated ones. In the current study, the data obtained by the partial slip model (Appendix C), which might be more reliable than the conventional GPT model, were used for further discussions. Looking into the data of the M-12, M-12-0.1-IC, M-12-0.2-IC and M-12-0.5-IC hollow fibers, rp increased from M-12 to M-12-0.1-IC and then kept decreasing from M-12-0.1-IC to M-12-0.5-IC with an increase in silicon rubber concentration in the coating solution. On the other hand, ε/lp, showed an opposite trend.
Table 3 Prediction of pore size and effective surface porosity by the partial slip model (ψ = 0.5), using helium as the probe gas at room temperature
| Membrane |
rp (nm) |
ε/lp (m−1) |
| M-12 |
193 ± 10 |
66.5 ± 10 |
| M-12-0.1-IC |
332 ± 40 |
5.91 ± 0.6 |
| M-12-0.2-IC |
290 ± 40 |
9.94 ± 1.5 |
| M-12-0.5-IC |
240 ± 15 |
21.7 ± 12 |
| M-15 |
148 ± 10 |
9.7 ± 2.0 |
| M-15-0.5-IC |
228 ± 10 |
2.8 ± 0.5 |
| M-15-0.5-WB |
864 ± 60 |
0.17 ± 0.04 |
| M-15-0.5-600B |
278 ± 30 |
9.15 ± 0.8 |
These observed trends were explained by assuming the penetration of the low viscosity and low surface tension silicon rubber solution (0.1%) deep into a large number of the small pores and, consequently, significant pore blocking. On the other hand, the penetration of the high viscosity and high surface tension silicon rubber solution (0.5%) was allowed to only enter the larger pores, with less severe pore blocking. The mode of pore blocking is schematically illustrated in Fig. 6 for: (a) uncoated membranes, (b) coated membranes via a coating solution of low silicon rubber concentration, and (c) coated membranes via a high silicon rubber concentration. These observations showed a significant influence of the silicon rubber layer even at very low concentration, which shows the role of this key-parameter in controlling the final performance properties of the membranes.
 |
| | Fig. 6 Tiny and large pores in the inner skin layer of the coated and uncoated membranes at different concentrations of silicon rubber solution, (a) uncoated, (b) 0.1 wt% or 0.2 wt% and, (c) 0.5 wt% (black: silicon rubber, gray: membrane matrix, white: pore channels). | |
4.2. Morphological study
Fig. 7 shows the SEM images of the cross-sections and the inner surfaces of the coated hollow fiber membranes. The SEM images were similar for all PEI coated hollow fibers. The cross-sections of the PEI membranes mostly show a thick layer of a finger like structure, which starts from both the outer and inner skins and meet with each other at the midway. According to the SEM images, since low concentrations of silicon rubber solution i.e. 0.1%, 0.2% and 0.5% w/w, were applied, the thickness of the silicon rubber layer is very tiny and is not clearly observable, it is noted that by applying a more powerful machine e.g. field emission scanning microscopy (FESEM), the thickness of the coating layer could probably be seen.
 |
| | Fig. 7 SEM images of the cross-section and the inner coated surface of (a) M-12-0.1-IC, (b) M-12-0.2-IC, and (c) M-12-0.5-IC. The magnifications of the top left inset images, from the left, are ×600, ×600 and ×800 respectively and the scale bar is 100 μm. | |
4.3. Wettability resistance
Table 4 shows the influence of different coating protocols on the contact angle and CEPw of the membranes. From Table 4, M-15 and M-12 membranes displayed contact angles of 82° and 78°, respectively. The silicon rubber coated membranes, on the other hand, exhibited much higher contact angles of above 108°. These results indicated that while the silicon rubber coating layer remained porous, even a thin layer of the coated PDMS (Fig. 7) could increase the contact angle significantly. Moreover, a very thin coated layer could substantially affect the hydrophobicity properties of the membranes and improve their wettability resistance by a large extent.
Table 4 Contact angles and CEPws of the coated and uncoated hollow fiber membranes
| Membrane code |
Contact angle (°) |
CEPw (kPa) |
| From ref. 34. |
| Dense PDMS |
106a |
— |
| M-15 |
82 ± 1.4 |
800 ± 50 |
| M-15-0.5-WB |
111 ± 2.9 |
800 ± 50 |
| M-15-0.5-600B |
114 ± 2.2 |
900 ± 50 |
| M-15-0.5-IC |
115 ± 2 |
1000 ± 50 |
| M-12 |
78 ± 3.4 |
300 ± 50 |
| M-12-0.1-IC |
108 ± 4.5 |
550 ± 50 |
| M-12-0.2-IC |
116 ± 1.7 |
600 ± 50 |
| M-12-0.5-IC |
114 ± 3.4 |
600 ± 50 |
Table 4 also includes the CEPw data of the coated and uncoated membranes. The CEPws for the uncoated membranes M-15 and M-12 were 800 and 300 kPa, respectively. Looking at the data for the M-12-IC (inside coating) series, an increase in the silicon rubber concentration results in an increased CEPw, eventually reaching 600 kPa for M-12-0.5-IC, which was a 100% increase relative to M-12. It is likely that an increase in the silicon concentration would result in an increase in the thickness of the silicon rubber layer, which in turn leads to the increase of the membrane CEPw. This was optimal with the contact angle of 114° for M-15-0.5-IC. According to Table 3, membrane M-12-0.1-IC had the highest mean pore size and the lowest surface porosity. As a result, the lowest gas permeance observed was due to the lowest surface porosity and the lowest CEPw measured was due to the highest mean pore size. Moreover, based on our observations, applying a different concentration of silicon rubber coating solution had two modes of action. First, increasing the concentration led to a decrease in the mean pore size and an increase in the surface porosity. Second, increasing the concentration resulted in the shifting of the surface property from hydrophilic to hydrophobic. Therefore, an increase in the silicon rubber solution caused an increase in the membrane CEPw. Since water was supplied into the lumen side of the hollow fiber, the effect of outside coating was much less pronounced. Based on the above observations, the coating technique showed significant dramatic changes in both the contact angles and CEPws for both the inside and outside coated hollow fiber membranes.
4.4. Membrane mass transfer resistance
In order to better understand the membrane mass transfer resistances (RM), a Wilson plot of 1/KOL versus v−α was used, Fig. 8. KOL was obtained from the experiments using eqn (4). As a result, the RM was obtained from the intercept of the Wilson plot. Among the various 1/KOL versus v−α correlations, an α value of almost 0.47 represented the best linear fit to the data points. The linear trend lines fitted through the experimental points are shown in Fig. 8 as well. It is noted that in the original Wilson plot, the predictions were based on an α value of 0.33.35 Atchariyawut et al.36 and Ismail and Mansourizadeh23 reported α values of 0.93 and 0.53 respectively for PVDF hollow fiber membranes. According to Fig. 8, the overall mass transfer resistance decreases as the concentration of the PDMS solution increases. Comparing the overall mass transfer resistance of the membranes, membrane M-12-0.5-IC exhibited the lowest resistance among the coated membranes. This was consistent with the gas permeation results in Fig. 4. Interestingly, the pore size and the effective porosity of this membrane were the largest and the contact angle was the highest (see Tables 3 and 4). This means that this membrane was the most efficient among all the other tested membranes.
 |
| | Fig. 8 Wilson plot of the fabricated membranes showing the effect of silicon rubber lumen side coating on the MCs overall mass transfer resistances (α ≈ 0.47). | |
The liquid mass transfer resistances associated with the uncoated and coated membranes can be estimated by the aid of the resistance-in-series model as well. The method of obtaining the individual resistances is as follows. Ignoring the contribution of gas phase resistance, the resistance-in-series model i.e. eqn (9) is applied as:
where
ROL and
RL are defined as
1/
KOL and
1/
kL, respectively.
KOL (and
ROL) is obtained from the experiments using
eqn (4).
RM was already obtained from the intercept of the Wilson plot in
Fig. 8. Hence, by subtracting
RM from
ROL, one can obtain the
RL at each desirable flow rate. The results for a liquid velocity of 3.0 m s
−1 are typically shown in
Table 5.
Table 5 Comparison between the membrane mass transfer resistances based on the gas absorption results and gas permeation results
| Membrane code |
Gas absorption approach (Wilson plot) |
Gas permeation approach |
| ROL (s m−1) |
RL (s m−1) |
RM (s m−1) |
kM (10−4 m s−1) |
rp (nm) |
ε/lp (m−1) |
DG (10−5 m2 s−1) |
RM (s m−1) |
kM (10−4 m s−1) |
| M-12 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 708 ± 1100 708 ± 1100 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 087 087 |
1621 |
4.75 |
193 ± 10 |
66.5 ± 10 |
1.2 |
374 |
8.01 |
| M-12-0.1-IC |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 175 ± 1300 175 ± 1300 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 970 970 |
3205 |
1.54 |
332 ± 40 |
5.91 ± 0.6 |
1.34 |
3712 |
0.81 |
| M-12-0.2-IC |
16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 556 ± 1100 556 ± 1100 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 622 622 |
2934 |
1.66 |
290 ± 40 |
9.94 ± 1.5 |
1.31 |
2293 |
1.31 |
| M-12-0.5-IC |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 831 ± 1200 831 ± 1200 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 337 337 |
1494 |
7.29 |
240 ± 15 |
21.7 ± 12 |
1.27 |
1090 |
2.75 |
The membrane mass transfer coefficient, as well as the membrane mass transfer resistance, can be estimated by applying the GPT results along with eqn (10) to (12) and (B5) to (B8). An acceptable agreement between the gas absorption approach and gas permeation approach can be achieved while the pores are fully filled with gas. Table 5 illustrates a good agreement between the two approaches, except for membrane M-12. The difference is most likely attributed to the partial pore wetting of membrane M-12, which resulted in a higher membrane mass transfer resistance during the gas absorption process. By comparing the membrane mass transfer resistances estimated by the two approaches depicted in Table 5, this phenomenon is revealed. It is noted that RL contributes to ROL more effectively than Rm. In addition, RL does not substantially depend on the membrane, which seems to be reasonable because the fluid dynamics of the liquid phase on the lumen side is almost the same for all hollow fibers. The authors believe that this is due to the liquid boundary layer resistance which is stronger than the membrane resistance. Moreover, the liquid phase mass transfer coefficient is a strong function of the turbulence, and in this case, the liquid boundary resistance was almost constant for all hollow fibers since it was kept constant at a liquid velocity of 3.0 m s−1. On the other hand, increasing the coating solution concentration, led to an increase in the effective porosity of the PDMS coated membranes, where the membrane mass transfer resistance experienced a decrease. The results given in Tables 3–5 show that the final performance of the PDMS coated membranes resulted from the simultaneous effect of the increase in the hydrophobicity character of the membranes combined with the decrease in the effective porosity of the membranes.
4.5. Membrane contactor performance
Fig. 9 shows the CO2 absorption flux vs. water velocity of the outside coated membranes in comparison to the uncoated one. The CO2 absorption flux depends on the type of the absorbent utilized, the system pressure and temperature, the membrane hydrophobicity (which controls the degree of partial wetting of the pores) and the membrane structural parameters (mean pore size and the effective porosity). From Fig. 9 it can be observed that the CO2 flux of membrane M-15-0.5-WB is lower than M-15. This is likely attributed to the blockage of the pore mouths on the outside surfaces of the hollow fibers by a silicon rubber layer, which results in the increase in the pore size as well as a decrease in the effective porosity (see Table 3 and Fig. 6b). This is also in good agreement with the GPT results as shown in Fig. 5 and Table 3. Conversely, the flux of M-15-0.5-600B was higher than that of M-15 due to the increase in both pore size and effective porosity (see Table 3). The surface contact angle also increased significantly from M-15 to M-15-0.5-600B (see Table 4). The increase in surface hydrophobicity was probably prevented by the partial pore wetting, which led to a significant increase in the membrane resistance against the pore wetting.
 |
| | Fig. 9 CO2 absorption flux vs. liquid velocity through the shell side, showing the effect of nitrogen blowing during the silicon rubber coating onto the outside surface of the 15% PEI hollow fiber membranes on the MCs performance. | |
Fig. 10 shows the performance of the uncoated membranes M-15 and M-12, in comparison to the silicon rubber coated membranes M-15-0.5-IC and M-12-0.5-IC.
 |
| | Fig. 10 CO2 absorption flux vs. liquid velocity through the lumen side, showing the effect of the silicon rubber lumen side coating on the MCs performance for 15% PEI and 12% PEI hollow fibers. | |
The flux of both the M-12 and M-15 hollow fibers were decreased slightly by the silicon rubber coating. However, the flux of the M-12-0.5-IC hollow fiber was several times higher than M-15-0.5-IC even after the silicon rubber coating. The trend of the absorption flux is in close agreement with the structural parameters shown in Table 5. Fig. 11 shows the effect of the inside silicone rubber coating on the hollow fiber performance. Fig. 11 exhibits the effect of different concentrations of the silicon rubber solution on the performance of the PDMS coated 12 wt% PEI membranes. The trend in the flux change observed in Fig. 11 parallels the change in ROL, which seems to be reasonable. The CO2 absorption flux of M-12-0.5-IC is the highest among all the coated membranes. Interestingly, M-12-0.2-IC and M-12-0.1-IC showed the same degree of performance, in terms of CO2 absorption flux, which is lower than the untreated membrane and the membrane M-12-0.5-IC. Most likely, the very low concentration of silicon rubber solution of 0.1 and 0.2 wt% penetrated through the pores of the membrane inner skin layer, blocking some of them as well as decreasing the pores sizes of others by coating the pore walls. This explanation is shown schematically in Fig. 6. This phenomenon can be true for membrane M-12-0.5-IC to a lower extent. Generally speaking, the decrease in the CO2 absorption flux is outweighed by the substantial enhancement in the membrane wetting resistance due to the higher contact angles and CEPws of the PDMS coated membranes. Fig. 10 also shows a comparison between the performance of the PVDF membranes fabricated by Mansourizadeh et al.37 and the fabricated membranes in the current work. The membranes fabricated by Mansourizadeh et al. showed a contact angle of 86° whereas the contact angles of the PDMS coated membranes are as high as 108°–116°, as shown in Table 4. Moreover, they reported a membrane mass transfer resistance of as high as 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 887 s m−1, significantly higher than the data presented in Table 5 in this work. Because of this, referring to Fig. 10, the performance of the membranes fabricated in the present study show a substantially (one order of magnitude) higher CO2 absorption flux in comparison to their membranes.
887 s m−1, significantly higher than the data presented in Table 5 in this work. Because of this, referring to Fig. 10, the performance of the membranes fabricated in the present study show a substantially (one order of magnitude) higher CO2 absorption flux in comparison to their membranes.
 |
| | Fig. 11 CO2 absorption flux vs. liquid velocity through the lumen side, showing the effect of the silicon rubber concentration on the MCs performance for 12 wt% PEI hollow fibers. | |
A comparison of Fig. 4 and 5 with Fig. 11 and 9 respectively shows that the effect of the silicon rubber coating on the CO2 absorption flux is less crucial than that on the helium gas permeance. This is postulated to be most likely due to the basic difference in the gas diffusion mechanisms between the gas permeance and the gas absorption flux. In the former, the transmembrane pressure difference is high e.g. up to 500 kPa so that the Knudsen and viscous diffusion are simultaneously controlling the gas permeation process. Meanwhile, in the latter, the value of the transmembrane pressure difference is much lower e.g. less than 50 kPa and the Knudsen and molecular diffusion are controlling the absorption flux. On the other hand, the CO2 permeability is much higher than the helium gas through the silicon rubber (2700/300, nine times),38 therefore the closed pores, combined with the open pores, participate in the mass transfer process to deliver a portion of CO2 to the other side of the membranes to enhance the gas absorption flux. Table 6 explains this fact in a more quantitative manner. Table 6 illustrates the ratio of (ε/lp)/(ε/lp)M-12, P/PM-12 calculated from the GPT results shown in Table 3 and J/JM-12 related to the gas absorption flux extracted from Fig. 11. The parameters without subscripts belong to the coated membranes. From Table 6, the trend of the ratios of the gas permeances (P/PM-12) are almost proportional to the ratios of the effective porosities ((ε/lp)/(ε/lp)M-12), whilst the ratio of the gas absorption fluxes (J/JM-12) are substantially higher, as well as more constant with respect to the ratio of gas permeation results, i.e. the effective porosities and the gas permeances.
Table 6 The effect of the silicon rubber coating on the helium GPT results and the carbon dioxide absorption flux
| Membrane code |
(ε/lp)/(ε/lp)M-12 |
P/PM-12 |
J/JM-12 (v = 3.0 m s−1) |
| M-12-0.1-IC |
0.014 ± 0.001 |
0.041 ± 0.003 |
0.669 ± 0.074 |
| M-12-0.2-IC |
0.150 ± 0.020 |
0.265 ± 0.033 |
0.633 ± 0.058 |
| M-12-0.5-IC |
0.326 ± 0.042 |
0.428 ± 0.060 |
0.825 ± 0.069 |
5. Conclusion
Based on the observations, the coating technique showed a significant change in the contact angles and CEPws of the coated membranes for the inside and outside coated hollow fiber membranes, while the silicon rubber coating layer remained porous. Disregarding the method of coating and even the polymer concentration, the contact angle was enhanced drastically from 82° (or 78°) up to at least 111° (or 108°). The CO2 absorption results revealed that by blowing nitrogen (600 kPa) through the lumen side of the hollow fibers during the PDMS coating process onto the membranes outside surface, the absorption flux of the membranes increased. A little decrease in the CO2 absorption flux for the other cases was outweighed by the substantial enhancement in the membrane wetting resistance due to the high contact angle and CEPw. It is believed that this was due to prohibiting the partial pore wetting of the membrane pores , which is a huge barrier across the mass transfer through the membranes. Based on this study, the increment in the ratio of the gas permeances were proportional to the ratio of the effective porosities, whilst the ratio of the gas absorption fluxes were substantially higher, as well as more constant, than the gas permeation results. This is most likely due to the involvement of the combination of closed pores and open pores in the mass transfer process to deliver CO2 to the other side of the membranes. This observation showed the high influence of the silicon rubber layer even at a very low concentration of silicon rubber solution on the CO2 gas absorption, which emphasizes the role of this key-parameter in controlling the final membrane contactor performance.
Appendix A: CO2 dissolution and dissociation in pure water
During the absorption process via pure water, the dissolved CO2 (CO2(l)) and the undissolved CO2 (CO2(g)) are in equilibrium and are related to each other by Henry’s law:where KH = 29.76 atm (mol−1 dm3) is the Henry constant of CO2 at atmospheric pressure and room temperature.26 At equilibrium, only a small fraction (ca. 0.2–1%) of the dissolved CO2 which is shown here by (CO2(l)) is actually converted to H2CO3:| | |
CO2(l) + H2O ↔ H2CO3(aq.)
| (A2) |
The hydration equilibrium constant of CO2 at room temperature [H2CO3(aq.)]/[CO2(l)] is almost 1.7 × 10−3,39 which reveals that the majority of the CO2 is not converted into carbonic acid, i.e. remaining in the molecular form CO2(molecular). As a result, CO2(l) = CO2(molecular) + H2CO3(aq.). Carbonic acid acts as a diprotic acid. Obviously, there are two dissociation constants corresponding to the number of valences. The first constant is responsible for the dissociation into the bicarbonate ion, HCO3−:
| | |
H2CO3(aq.) ↔ HCO3− + H+
| (A3) |
whose dissociation constant is equal to 2.5 × 10
−4.
38 While applying the first dissociation constant, as mentioned above, CO
2 dissolved in the molecular form (CO
2(molecular)) is in equilibrium with the dissociable form as carbonic acid (H
2CO
3(aq.)) in the aqueous form. Consequently, H
2CO
3 (with no subscript) combines the dissolved CO
2 both the molecular form and the dissociable forms. Therefore, to cover the two forms of CO
2 presented in pure water,
eqn (A3) can be rearranged as follows:
whose apparent dissociation constant is equal to 4.45 × 10
−7.
40
The second dissociation constant is responsible for the production of the carbonate ion, CO32−:
whose dissociation constant is equal to 4.70 × 10
−11.
40
Applying eqn (A1) and (A3) to (A5), along with the dissociation equation of water [H+][OH−] = 10−14, and the system overall charge balance equation [H+] = [OH−] + [HCO3−] + 2[CO32−], the system of equations is closed.
Appendix B: predicting the mass transfer and diffusion coefficients
An approximate solution for the differential equation driven from the continuity equation was proposed by Graetz for small values of the Graetz number, Gz (d2v/LDL), by which the average and the local Sherwood number, Sh (kL/dhD), can be obtained as follows:29where v is liquid velocity in the lumen side (m s−1), DL (m2 s−1) is the diffusion coefficient of CO2 in liquid phase, kL is liquid boundary layer mass transfer coefficient (m s−1) and dh is the hydraulic diameter (m).
Another solution was given by the Leveque equation.29 The approximate solution proposed by Leveque to the system is based on the assumption that the concentration boundary layer is limited to a thin layer adjacent to the wall of the fiber. This assumption is valid for high mass velocities through relatively short fibers in laminar flow.30 Therefore, the Leveque equation is mostly applicable for Gz exceeding 20. According to Leveque, Sh is given by:
| | |
Sh = 1.62Gz1/3, Gz > 20
| (B2) |
Many researchers have experienced that for the flow of aqueous solutions at atmospheric pressures, a combination of the Graetz and Leveque solutions can be effective to predict the lumen-side mass transfer coefficient for gas filled pores. Kreulen et al.31 gave the generalized solution of Graetz–Leveque equation by the curve fitting of eqn (B1) and (B2) against experimental data:
| |
 | (B3) |
In contrast, for the shell side mass transfer coefficient, no common model is available to describe the mass transfer coefficient, most likely because of ununiformed distribution of liquid flow, the presence of dead zones, channeling, splitting etc.27 These are broadly due to the uneven fiber distribution inside the membrane module. One of the most commonly used models is the model proposed by Yang and Cussler:32
| | |
Sh = 1.25(Redsh/L)0.93Sc0.33
| (B4) |
where Re (
ρLvdh/
μ) is the shell side Reynolds number, and Sc (
μ/
ρLDL) is the liquid Schmidt number.
ρL is liquid density (kg m
−3), and
μ is the liquid viscosity (Pa s).
The molecular diffusion coefficient (DM) can be easily calculated by the Chapman and Cowling33 equation:
| |
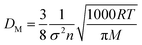 | (B5) |
with
| |
 | (B6) |
and
| |
 | (B7) |
where
σ is the molecular size which is equal to 3.3 × 10
−10 m for CO
2,
n is the number density (m
−3),
P is the average pressure between the upstream and downstream (Pa),
ρg is the gas density (kg m
−3),
Z is the
z-factor which approaches unity for an ideal gas, and
R is the universal gas constant (8.314 Pa m
3 mol
−1 K
−1).
The Knudsen diffusion coefficient (DK) is calculated by:33
| |
 | (B8) |
Appendix C: pore size and effective porosity
The results of the GPT were used to calculate the pore size and effective porosity. In the GPT, it was assumed that the pores are cylindrical and straight and the gas flows through the pores. The partial slip model41,42 was applied to determine the mean pore size and effective porosity. This model demonstrates the nonlinear trend of the data, especially in the range of the transition flow between the free molecular regime and the viscous flow regime. The required equations are as follows:| |
 | (C1) |
| |
 | (C2) |
and| |
 | (C3) |
where ε is the membrane surface porosity, lp is the pore length (m) and the ratio ε/lp is called the effective porosity. M is the molecular weight (kg kmol−1) and μ is the gas viscosity (Pa s). ϕ is called the wall-molecule collision probability function which shows the nonlinearity of the gas permeance versus the average pressure, due to the pressure dependency of the slope, and ψ is a factor which shows the extent of the slip flow regime, supposed to be 0.0 < ψ < 1.0. Here, ψ has been assumed to be 0.5. Kn is the Knudsen number and λ is the gas mean free path (m) given by the kinetic theory of gases:| |
 | (C4) |
where kB is the Boltzmann constant (equal to 1.38 × 10−23 J K−1), σ is the collision diameter (m) and P is system mean pressure (Pa).43 The details of the derivation of these equations and the simple algorithm utilized to solve rp and ε/lp were presented elsewhere.41
Nomenclature
| A | Effective membrane area (m2) |
| CiG | Concentration of CO2 at the liquid/gas interface for gas phase (mol m−3) |
| CinL | Inlet concentration of CO2 in solution (mol m−3) |
| Cin,iL | Inlet concentration of CO2 in liquid/gas interface (mol m−3) |
| CoutL | Outlet concentration of CO2 in solution (mol m−3) |
| Cout,iL | Outlet concentration of CO2 in liquid/gas interface (mol m−3) |
| (ΔClm) | Log-mean concentration difference |
| d | Inside or outside fiber diameter (m) |
| dh | Hydraulic diameter (m) |
| di, do and dlm | Hollow fiber inside, outside and log mean diameters (m) |
| DG | Diffusion coefficient of gas (m2 s−1) |
| DK | Knudsen diffusion coefficient (m2 s−1) |
| DL | Diffusion coefficient of CO2 in liquid phase (m2 s−1) |
| DM | Molecular diffusion (m2 s−1) |
| Gz | Graetz number |
| H | Dimensionless temperature-dependent Henry constant |
| h | Henry constant (MPa) |
| I | Intercept |
| J | Total absorption flux (mol m−2 s−1) |
| kB | Boltzmann constant (equal to 1.38 × 10−23 J K−1) |
| kG | Gas boundary layer mass transfer coefficient (m s−1) |
| kL | Liquid boundary layer mass transfer coefficient (m s−1) |
| kM | Membrane mass transfer coefficient (m s−1) |
| Kn | Knudsen number |
| KOL | Overall mass transfer coefficient based on the liquid phase (m s−1) |
| L | Length of the fibers (m) |
| lp | Pore length (m) |
| M | Molecular weight (kg kmol−1) |
| n | Number of hollow fibers, gas number density (m−3) |
| P | Total permeance (mol m−2 Pa−1 s−1) |
| P | System mean pressure (Pa) |
| ΔP | Transmembrane pressure drop |
| QL | Liquid volumetric flow rate (m3 s−1) |
| R | Universal gas constant (8.314 J mol−1 K−1) |
| Re | Shell side Reynolds number |
| RL | Liquid boundary layer mass transfer resistance (s m−1) |
| RM | Membrane mass transfer resistance (s m−1) |
| ROL | Overall membrane mass transfer resistance (s m−1) |
| rp | Pore radius |
| S | Slope |
| Sc | Liquid Schmidt number |
| Sh | Sherwood number |
| t | Permeation time (s) |
| T | System absolute temperature (K) |
| V | Volume of gas permeated through the membrane (m3, STP) |
| Z | z-Factor |
| ε | Membrane surface porosity |
| ε/lp | Effective porosity |
| ϕ | Wall-molecule collision probability function |
| λ | Gas mean free path (m) |
| μ | Gas viscosity (Pa s) |
| ρL | Liquid density (kg m−3) |
| ρG | Gas density (kg m−3) |
| σ | Collision diameter (m) |
| σ | Molecular size (m) |
| τ | Tortuosity |
| v | Liquid velocity in lumen (m s−1) |
| ψ | Slip flow regime factor |
References
- D. de Montigny, P. Tontiwachwuthikul and A. Chakma, Comparing the absorption performance of packed columns and membrane contactors, Ind. Eng. Chem. Res., 2005, 44, 5726–5732 CrossRef CAS.
- S. Mosadegh-Sedghi, D. Rodrigue, J. Brisson and M. C. Iliuta, Wetting phenomenon in membrane contactors – causes and prevention, J. Membr. Sci., 2014, 452, 332–353 CrossRef CAS PubMed.
- S. Khaisri, D. deMontigny, P. Tontiwachwuthikul and R. Jiraratananon, A mathematical model for gas absorption membrane contactors that studies, the effect of partially wetted membranes, J. Membr. Sci., 2010, 347, 228–239 CrossRef CAS PubMed.
- M. Stanojevic, B. Lazarevic and D. Radic, Review of membrane contactors designs and applications of different modules in industry, FME Transactions, 2003, 31, 91–98 Search PubMed.
- M. Mulder, Basic Principles of Membrane Technology, Kluwer, Dordredcht, 2nd edn, 1996, ch. 6, pp. 280–412 Search PubMed.
- M. Rezaei, A. F. Ismail, G. Bakeri, S. A. Hashemifard and T. Matsuura, Effect of General Montmorillonite and Cloisite 15A on Structural Parameters and Performance of Mixed Matrix Membranes Contactor for CO2 Absorption, Chem. Eng. J., 2015, 260, 875–885 CrossRef CAS PubMed.
- H. Kreulen, C. A. Smolders, G. F. Versteeg and W. P. M. van Swaaij, Determination of mass transfer rates in wetted and non-wetted microporous membranes, Chem. Eng. Sci., 1993, 48, 2093–2102 CrossRef CAS.
- Y. Zhang, R. Wang, S. Yi, L. Setiawan, X. Hu and A. G. Fane, Novel chemical surface modification to enhance hydrophobicity of polyamide-imide (PAI) hollow fiber membranes, J. Membr. Sci., 2011, 380, 241–250 CrossRef CAS PubMed.
- P. T. Nguyen, E. Lasseuguette, Y. Médina, J. C. Remigy, D. Roizard and E. Favre, A dense membrane contactor for intensified CO2 gas/liquid absorption in post-combustion capture, J. Membr. Sci., 2011, 337, 261–272 CrossRef PubMed.
- G. Bakeri, T. Matsuura, A. F. Ismail and D. Rana, A novel surface modified polyetherimide hollow fiber membrane for gas–liquid contacting processes, Sep. Purif. Technol., 2012, 89, 160–170 CrossRef CAS PubMed.
- B. Ozturk, H. B. Al-Saffar and R. Hughes, Sulphur dioxide absorption in hollow fibre membrane modules, Chem. Eng. Commun., 2000, 177, 157–175 CrossRef CAS PubMed.
- H. Kreulen, C. A. Smolders, G. F. Versteee and W. P. M. van Swaaij, Microporous hollow fibre membrane modules as gas liquid contactors part 2. Mass transfer with chemical reaction, J. Membr. Sci., 1993, 78, 217–238 CrossRef CAS.
- T. Papadopoulos and K. K. Sirkar, A modified hollow fiber contained liquid membrane technique for gas separation at high pressures, J. Membr. Sci., 1994, 94, 163–181 CrossRef CAS.
- D. G. Bessarabov, E. P. Jacobs, R. D. Sanderson and I. N. Beckman, Use of nonporous polymeric flat-sheet gas-separation membranes in a membrane-liquid contactor: experimental studies, J. Membr. Sci., 1996, 113, 275–284 CrossRef CAS.
- D. C. Nymeijer, T. Visser, R. Assen and M. Wessling, Composite hollow fiber gas–liquid membrane contactors, for olefin/paraffin separation, Sep. Purif. Technol., 2004, 37, 209–220 CrossRef CAS PubMed.
- K. Kneifel, S. Nowak, W. Albrecht, R. Hilke, R. Just and K.-V. Peinemann, Hollow fiber membrane contactor for air humidity control: Modules and membranes, J. Membr. Sci., 2006, 276, 241–251 CrossRef CAS PubMed.
- Z. Jin, D. L. Yang, S. H. Zhang and X. G. Jian, Hydrophobic modification of poly(phthalazinone ether sulfone ketone) hollow fiber membrane for vacuum membrane distillation, J. Membr. Sci., 2008, 310, 20–27 CrossRef CAS PubMed.
- P. T. Nguyen, E. Lasseuguette, Y. Medina-Gonzalez, J. C. Remigy, D. Roizard and E. Favre, A dense membrane contactor for intensified CO2 gas/liquid absorption in post-combustion capture, J. Membr. Sci., 2011, 377, 261–272 CrossRef CAS PubMed.
- S. P. Yan, M. X. Fang, W. F. Zhang, S. Y. Wang, Z. K. Xu, Z. Y. Luo and K. F. Cen, Experimental study on the separation of CO2 from flue gas using hollow fiber membrane contactors without wetting, Fuel Process. Technol., 2007, 88, 501–511 CrossRef CAS PubMed.
- W. Rongwong, R. Jiraratananona and S. Atchariyawut, Experimental study on membrane wetting in gas–liquid membrane contacting process for CO2 absorption by single and mixed absorbents, Sep. Purif. Technol., 2009, 69, 118–125 CrossRef CAS PubMed.
- R. Faiz and M. Al-Marzouqi, CO2 removal from natural gas at high pressure using membrane contactors: model validation and membrane parametric studies, J. Membr. Sci., 2010, 365, 232–241 CrossRef CAS PubMed.
- J. G. Lu, Y. F. Zheng and M. D. Cheng, Wetting mechanism in mass transfer process of hydrophobic membrane gas absorption, J. Membr. Sci., 2008, 308, 180–190 CrossRef CAS PubMed.
- A. F. Ismail and A. Mansourizadeh, Comparative study on the structure and performance of porous polyvinylidene fluoride and polysulfone hollow fiber membranes for CO2 absorption, J. Membr. Sci., 2010, 365, 319–328 CrossRef CAS PubMed.
- S. Ma’mun, H. F. Svendsen, K. A. Hoff and O. Juliussen, Selection of new absorbents for carbon dioxide capture, Energy Convers. Manage., 2007, 48, 251–258 CrossRef PubMed.
- S. R. Wickramasinghe, M. J. Semmens and E. L. Cussler, Mass transfer in various hollow fiber geometries, J. Membr. Sci., 1992, 69, 235–250 CrossRef CAS.
- J. J. Carroll, J. D. Slupsky and A. E. Mather, The solubility of carbon dioxide in water at low pressure, J. Phys. Chem. Ref. Data, 1991, 20, 1201–1209 CrossRef CAS PubMed.
- E. Drioli, A. Criscuoli and E. Curcio, Membrane contactors: Fundamentals, applications and potentialities, Elsevier, Amsterdam, 2006, ch. 4, pp. 127–162 Search PubMed.
- V. Y. Dindore, D. W. F. Brilman, F. H. Geuzebroek and G. F. Versteeg, Membrane–solvent selection for CO2 removal using membrane gas–liquid contactors, Sep. Purif. Technol., 2004, 40, 133–145 CrossRef CAS PubMed.
- P. S. Kumar, J. A. Hogendoorn, P. H. M. Feron and G. F. Versteeg, Approximate solution to predict the enhancement factor for the reactive absorption of a gas in a liquid flowing through a microporous membrane hollow fiber, J. Membr. Sci., 2003, 213, 231–245 CrossRef CAS.
- V. Y. Dindore, D. W. F. Brilman, P. H. M. Feron and G. F. Versteeg, CO2 absorption at elevated pressures using a hollow fiber membrane contactor, J. Membr. Sci., 2004, 235, 99–109 CrossRef CAS PubMed.
- H. Kreulen, C. A. Smolders, G. F. Versteeg and W. P. M. van Swaaij, Microporous hollow fiber membrane modules as gas–liquid contactor. Part 1. Physical mass transfer processes, J. Membr. Sci., 1993, 78, 197–216 CrossRef CAS.
- M. C. Yang and E. L. Cussler, Designing hollow-fiber contactors, AIChE J., 1986, 32, 1910–1916 CrossRef CAS PubMed.
- R. M. A. Roque-Malherbe, The Physical Chemistry of Materials: Energy and Environmental Applications, CRC press, London, 2010, ch. 5, pp. 217–271 Search PubMed.
- P. Ferreira, A. Carvalho, T. R. Correia, B. P. Antunes, I. J. Correia and P. Alves, Functionalization of polydimethylsiloxane membranes to be used in the production of voice prostheses, Sci. Technol. Adv. Mater., 2013, 14, 1–8 CrossRef.
- E. E. Wilson, A basis for rational design of heat transfer apparatus, Trans. ASME, 1915, 37, 47 Search PubMed.
- S. Atchariyawut, R. Jiraratananon and R. Wang, Mass transfer study and modeling of gas–liquid membrane contacting process by multistage cascade model for CO2 absorption, Sep. Purif. Technol., 2008, 63, 15–22 CrossRef CAS PubMed.
- A. Mansourizadeh, A. F. Ismail, M. S. Abdullah and B. C. Ng, Preparation of polyvinylidene fluoride hollow fiber membranes for CO2 absorption using phase-inversion promoter additives, J. Membr. Sci., 2010, 355, 200–207 CrossRef CAS PubMed.
- R. W. Baker, Membrane technology and applications, John Wiley & Sons, New York, 2nd edn, 2004, ch. 8, pp. 301–353 Search PubMed.
- B. E. Poling, J. M. Prausnitz and J. P. O’Connell, The Properties of Gases and Liquids, McGraw-Hill, Boston, 5th edn, 2001, ch. 8, pp. 1–193 Search PubMed.
- D. A. Skoog, D. M. West and F. J. Holler, Fundamentals of analytical chemistry, Sunders college publishing, New York, 6th edn, 1992, appendix A Search PubMed.
- S. A. Hashemifard, A. F. Ismail, T. Matsuura and N. Hilal, Predicting the structural parameters of integrally skinned porous membranes, J. Membr. Sci., 2014, 454, 451–462 CrossRef CAS PubMed.
- D. L. Wang, R. X. Xu, G. L. Jiang and B. L. Zhu, Determination of surface dense layer structure parameters of the asymmetric membrane by gas permeation method, J. Membr. Sci., 1990, 52, 97–108 CrossRef CAS.
- R. B. Bird, W. E. Stewart and E. N. Lightfoot, Transport phenomena, John Wiley & Sons, New York, 2nd edn, 2002, ch. 1, pp. 11–39 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2015 |
Click here to see how this site uses Cookies. View our privacy policy here. 
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 325 is the absolute atmospheric pressure of the permeate side in Pa.
325 is the absolute atmospheric pressure of the permeate side in Pa.



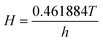







![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 708 ± 1100
708 ± 1100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 087
087![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 175 ± 1300
175 ± 1300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 970
970![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 556 ± 1100
556 ± 1100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 622
622![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 831 ± 1200
831 ± 1200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 337
337
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 887 s m−1, significantly higher than the data presented in Table 5 in this work. Because of this, referring to Fig. 10, the performance of the membranes fabricated in the present study show a substantially (one order of magnitude) higher CO2 absorption flux in comparison to their membranes.
887 s m−1, significantly higher than the data presented in Table 5 in this work. Because of this, referring to Fig. 10, the performance of the membranes fabricated in the present study show a substantially (one order of magnitude) higher CO2 absorption flux in comparison to their membranes.