Removal of heavy metals from water through armchair carbon and boron nitride nanotubes: a computer simulation study

Abstract

Molecular dynamics simulations are used to study the removal of heavy metals from water using armchair carbon and boron nitride nanotubes and to analyse the transport of water molecules through the nanotubes under an applied electric field. The system includes a mixture of three heavy metals (Cu²⁺, Hg²⁺ and Pb²⁺) and a (7,7) carbon nanotube or a (7,7) boron nitride nanotube embedded in a silicon nitride membrane. An external electric field is applied to the simulated system for transporting ions. The results of the study indicate that the (7,7) nanotubes are capable of removing heavy metals with different ratios. The simulation results reveal that the removal of cations through armchair carbon and boron nitride nanotubes is attributed to the applied electric field. The phenomenon is explained with the potential of mean force. Moreover, the ionic current, water flow, normalized transport rate of water, and ion retention time are measured.

---

1. Introduction

Transporting fluids through narrow channels and separating ions are now highly related to industrial processes, and have attracted great attention in recent years as important research issues.^1–3 Moreover, the development of low-cost water treatments and the separation of heavy hazardous metals, such as copper, mercury and lead, from water are of high significance. Disappointingly, the majority of the methods proposed for removing heavy metals contain complex procedures, and make it difficult to completely understand the transport properties. Heavy metal separation from water in a structurally controllable modelling system, where the conditions and parameters of the system can be suitably modified by experimental methods, thus has been a target of many studies in this area.

Although human body needs small amounts of heavy metals, high doses of them can be harmful. The presence of toxic heavy metals in water can cause many serious problems in human body. Hence, separating these materials from water is considered to be a critical issue.^4–7 A number of methods have been proposed for removing heavy metals from water, including ion-exchange,⁸ coagulation and flocculation,⁹ chemical precipitation,¹⁰ reverse osmosis,¹¹ adsorption.¹² Separating ions, especially heavy metals from water with nanotubes, is a promising method, which has been applied in a wide range of sciences. Ion selectivity is defined as the ability of a pore to pass or reject ions. Nanotubes are capable of acting as a selective pore to replicate this property. They have many applications in the water treatment industry. Considering the efficient applications of nanotubes, we use two types of armchair nanotubes in the present study, namely carbon nanotube (CNT) and boron nitride nanotube (BNNT).

Due to their nano scale diameters, the use of CNTs is considered as a controversial issue in the water treatment industry. Since CNTs discovery,¹³ numerous studies have been carried out.^14–16 It can be hypothesized that separating ions and transporting water across CNTs is a complex issue. CNTs are considered as appropriate and capable nanomaterials for water treatment industries. Nanotube diameter is regarded as an effective parameter in ion separation phenomenon. Related studies indicate that specific ions are allowed to pass through CNTs and water molecules with different arrangements can pass through them. Corry investigated salt rejection of armchair CNTs under a hydrostatic pressure.¹⁷ Hence, a number of studies have recommended CNTs as a device for ion separation.^18–20

BNNTs are widely used by researchers due to their properties and structural uses.²¹ These nanotubes were first theoretically predicted in 1994,²² and were experimentally synthesized.²³ Researchers use BNNTs for designing ion-selective devices.^24–26 Won and Aluru studied the ionic selectivity of BNNTs in relation to chloride and potassium ions.²⁴ They immersed a (10,10) BNNT in a reservoir of potassium chloride solution to investigate its ionic selectivity. They found that the (10,10) BNNT was capable of conducting chloride ions but potassium ions were not. In another study, water properties inside CNT and BNNT with different diameters were investigated.²⁷

Regarding ion selectivity through CNTs and BNNTs, several parameters, such as size exclusion, dehydration and charge repulsion, can be effective.²⁸ In the case of size exclusion parameter, it should be mentioned that if the size of ions is larger than the diameter of nanotubes, they will not be able to enter the nanotubes. The cations or anions tend to be surrounded by a hydration shell that makes powerful interaction between ions and water. In larger nanotubes, ions are able to cross nanotubes with their full solvation shell. In contrast, if nanotube diameter becomes smaller than the size of ion solvation shell, some water molecules should be removed from ion hydration shell. In this case, the ions will be able to pass through the nanotube. The removal of water molecules from ion hydration shell requires spending energy which is a factor for ion rejection. As the nanotube diameter decreases or increases, ion rejection rate rises or falls, respectively.^29,30

With respect to the review of the literature, we use molecular dynamics (MD) simulation here to study the separation of heavy metals from water through a membrane, containing carbon or boron nitride nanotubes. MD simulation is a computer-based simulation method that provides a controlling instrument for studying and investigating the permeation, separation and selectivity of numerous nanotubes. In MD simulations, species motion is followed and examined over time, and the interactions between them are described by empirical potentials. The trajectories of the species are investigated to specify the structural and dynamic properties of the system. To study ion separation by nanotubes under an electric field, nanotubes should be arranged to form a membrane that can separate two reservoirs. In line with this objective, we used CNT and BNNT with (7,7) chirality. Then, we fixed them in a silicon nitride (SiN) membrane and immersed them in a mixture of CuCl₂, HgCl₂ and PbCl₂ aqueous solution (see Fig. 1).

Fig. 1 A snapshot of the simulated system (licorice: (7,7) BNNT; tan: SiN membrane; orange: Cu²⁺; blue: Pb²⁺; yellow: Hg²⁺; green: Cl⁻; red: O; and white: H).

The length of the nanotubes was 15 Å. The radii of the (7,7) CNT and the (7,7) BNNT are 4.755 Å and 4.89 Å, respectively. The results of the present study not only contribute to understanding heavy metal separation through nanotubes but also show the structure and dynamics of water molecules in these nanotubes.

2. Simulation methodology

2.1. Initial structures

MD simulations were performed to separate ions by means of different nanotubes in different voltages. In line with this purpose, the (7,7) CNT and the (7,7) BNNT were selected. The geometries of the selected nanotubes were optimized in the GAMESS-US³¹ at the B3LYP level of theory using the 6-31G(2d,2p) basic set. The SiN membrane with appropriate pore for different types of nanotubes was fabricated using the method outlined in the bio nanotechnology NAMD tutorial. Then, the selected nanotubes were embedded in it. The water molecules and the desired ions were also added to the system.

2.2. System setup

The simulated system included a nanotube immersed in a SiN membrane, water, and ions. In many experimental studies nanotubes are generally embedded in the SiN³² or a polystyrene film.^33,34 However, in MD simulation-based studies, nanotubes are typically embedded in a variety of membranes including SiN membrane,³⁵ lipid bilayers,³⁶ and graphene bilayers.³⁷ The number of water molecules in the simulation box was approximately 1120. Also the investigated system included 0.5 M mixed aqueous solution. The center of the nanotubes was set as the center of the simulation box. Nanotubes embedded in the SiN membrane were placed in the center of the box at the position of x, y, z = 0. The axes of the nanotubes were parallel to the z-axis of the box, and an electric field was applied in the z direction of the system. For carbon, boron and nitrogen atoms, the Lennard-Jones parameters were adopted from ref. 38 and 39. The Lennard-Jones parameters for heavy metals were obtained from.⁴⁰

In this study, the carbon atoms in the CNTs were assumed to be uncharged Lennard-Jones particles,⁴¹ and the partial charges for BNNTs were determined by DFT method using CHelpG (Charges from Electrostatic Potentials using a Grid based method) scheme developed by Breneman and Wiberg.⁴² The partial charges obtained from DFT method that used in the MD simulation were −0.4, +0.4 and zero for nitrogen, boron and carbon atoms, respectively. As expected, the boron atoms with a lower electronegativity compared to the nitrogen atoms are positively charged while the nitrogen atoms are negatively charged in B–N bonding. The values of 1.420 Å and 1.446 Å were obtained as the optimized C–C and B–N bonds distance, respectively. The parameters for the 12–6 Lennard-Jones potential were σ_carbon = 3.369 Å, σ_boron = 3.453 Å, σ_nitrogen = 3.365 Å, ε_carbon = 0.0607 kcal mol⁻¹, ε_boron = 0.0949 kcal mol⁻¹, ε_nitrogen = 0.1448 kcal mol⁻¹. The calculation of charge values by different method do not influence in the results. Also, the interaction parameters between different species of the system were obtained using Lorentz–Berthelot combining rules. MD simulations were carried out at temperature (298 K) using the Langevin dynamics method for temperature coupling, and the Nose–Hoover Langevin piston was used to maintain the pressure at 1 bar. All MD simulations were performed in the canonical (NVT) ensemble with periodic boundary conditions in all the three-directions with the NAMD 2.9 (ref. 43) with a 1 fs time step and VMD1.9.2 (ref. 44) was used to visualize the simulations, as in our previous works.^45–48 The TIP3P water model was used to represent water molecules.⁴⁹ The van der Waals interactions were truncated by a 12 Å cutoff. The Particle Mesh Ewald method⁵⁰ was used to treat long-range electrostatic calculations. The CNT or BNNT and SiN membrane were restrained with a harmonic constraint. The simulation box for all runs was 3.6 × 4 × 5 nm³, and the system was subjected to a zero-temperature energy minimization for 1 ns and then it was equilibrated with molecular dynamics for 5 ns at 298 K before collecting data. The data were then collected every 0.1 ps. The CHARMM force field⁵¹ was employed for all atoms. An electrical field was applied for all considered systems within the whole simulation period. The applied electrical field was represented in internal units of NAMD package, which could be defined by eqn (1).

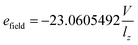where e_field, V and l_z are the applied electrical field (in kcal mol⁻¹ Å⁻¹ e⁻¹), potential difference (in volt) and size of the system along the z-axis (in Ångstrom).

2.3. Ion current

An electric field (voltage) was applied to the simulation system. Due to the applied electric field, the ions were passing through the nanotubes. As a result of this phenomenon, system current could be measured. The current versus voltage curve was obtained for the respective systems at an ionic concentration of 0.5 mol L⁻¹. The amount of current (I) was calculated by eqn (2).

I = NQ/ΔT (2)

where N refers to the average number of heavy metals that cross the considered nanotubes, Q stands for the charge of the ion, and ΔT refers to the simulation time, respectively.

2.4. Potential of mean force calculations

The ion permeation through the (7,7) CNT and the (7,7) BNNT was investigated by calculating the potential mean force (PMF)⁵² along the z-axis of the simulation box. Umbrella sampling method was used to measure the PMFs of the ions, which were moving across the nanotubes,⁵³ and the data were analysed using the weighted histogram analysis method (WHAM).⁵⁴ After averaging the force on the ions at different z positions along the nanotube axis, PMF was calculated by means of integrating the mean force along the z-axis. The ions were moved from the position −7.5 Å to the position 7.5 Å in 0.5 Å increments. In each simulation, the z coordinate of ions was held constant using a 12.5 kcal mol⁻¹ Å⁻² harmonic constraint while the ion was free to move radially. The constant force yields sufficient overlaps for the probability distributions. Prior to all simulations, the test ion(s) were held fixed for 10 ps to allow water to equilibrate around it. A total of 31 windows were carried out. Each sampling window was run for 1 ns.

3. Results and discussion

According to the water treatment perspective, it is important to understand the separation properties of heavy metals and the transport of water molecules through nanotubes. Although remarkable advances have been recently made on this research issue, understanding the effects of nanotubes on heavy metal separation still remains to be an open question. With this research gap in mind, we performed MD simulations in this study to investigate the separation of heavy metals from water across (7,7) CNT and (7,7) BNNT. To this end, some properties of the simulated system including ionic current, water flow rate, normalized transport rate of water, and ion retention time were investigated.

3.1. PMF for ions

Although the (7,7) CNT and the (7,7) BNNT have spaces that are big enough for all ions to go through them, the results of the present study indicate that only cations enter the nanotubes and chlorine ions cannot enter the nanotubes. In related research papers, the ability to separate ions was investigated by calculating PMF for ions.⁵² Fig. 2 displays the PMF curves for the experiments ions.

Fig. 2 The potential of mean force for heavy metals and chlorine in (a) (7,7) CNT; and (b) (7,7) BNNT.

As it can be observed in Fig. 2, a deep potential well was produced for heavy metals in the (7,7) nanotubes. The silicon nitride membrane atoms lied in the immediate neighbourhood of nanotubes control the type of ions entering into nanotubes. Since all ions have roughly the same potential well, separating Cu²⁺, Hg²⁺ and Pb²⁺ ions through the nanotubes in each electric field cannot be distinguished, and these cations were crossed from nanotubes with different proportions.

3.2. Water transport and its properties

In most computational studies investigating water flow through CNTs, the partial charge of each carbon atom was assumed to be zero.¹⁷ Hence, there is no electrostatic interaction between CNT and water molecules. As a result, only van der Waals interactions are realized, which is regarded as a weak interaction.⁵⁵ Weak interactions lead to a lack of friction between CNT wall and water molecules. In such conditions, the water flow rate through CNT increases. In contrast with CNT, partial charges of boron and nitrogen atoms in the case of BNNT are not zero. Partial charges on the BNNT walls can reduce the BNNT entrance barrier for water molecules from bulk.⁵⁶ As a result, it can be maintained that reducing barriers increases the water flow rate.

Water molecules can spontaneously get into nanotubes with diameters greater than 8.1 Å. Water molecules can remain inside nanotubes or get out of them.¹⁷ However, in the case of narrower nanotubes such as (5,5), water molecules partially enter them.³⁹ Since large nanotubes were used in the present study, water molecules could pass through them. If the pressure was applied on system, water molecules pass under pressure, but in this study, water transport is due to the ion transport. Water flow rate was defined as the total number of water molecules moving through the nanotube from −z to +z per unit of time. Fig. 3 demonstrates the flow rate of water molecules.

Fig. 3 Flow rate of water in the (7,7) CNT and the (7,7) BNNT.

Due to the partial charges of (7,7) BNNT, the amount of water flow rate through this nanotube was higher than that of the (7,7) CNT. Each carbon atom of (7,7) CNT was assumed to be neutral in MD simulations, but boron and nitrogen atoms of (7,7) BNNT had partial charges, which caused water molecules to hydrogen-bond with nitrogen atoms.⁵⁷ Thus it can be argued that in simulation studies BNNT is spontaneously filled more than CNT.

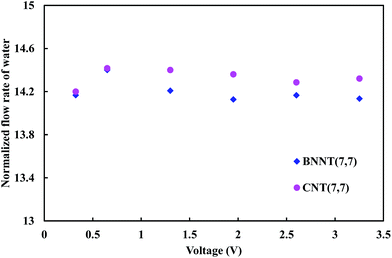
Fig. 4 depicts the normalized flow rate of water molecules with respect to the number of transported ions. The results indicate that the normalized flow rate of water (transported water for one permeated ion) is independent of the applied electric field.

Fig. 4 Normalized flow rate of water in the studied systems.

Moreover, although there are not significant differences between BNNT and CNT in terms of normalized water flow rate, there are still differences between them. It is attributed to the low number of ions passing through the CNT in comparison to the BNNT.

The water network structure inside the nanotubes resulted in the creation of hydrogen bonds between water molecules. Since increasing the voltage applied to the system leads to an increase in the number of water molecule through the nanotubes, hence, the number of hydrogen bonds will also increase. As Fig. 5 illustrates, this enhanced the number of hydrogen bonds between the inner water molecules.

Fig. 5 Hydrogen bonds between inner water molecules of nanotubes.

For explain the strength of the interactions between CNT/BNNT with ions, we calculated PMF as shown in Fig. 2. All ions have roughly the same strength of the interactions with nanotubes. For the strength of the interactions between CNT/BNNT with water molecules we used the NAMD Energy plugin in VMD. The NAMD Energy plugin provides both a graphical user interfaces and text commands for evaluating energies using NAMD. NAMD Energy applies the desired energy calculations to each frame of the selected molecule, unless a different frame skip parameter is selected. These results were shown in Fig. 6(a). As can be seen in this figure, interaction energy between water molecules with BNNT is stable than that of with CNT. This trend of interaction energy can be clarified by radial distribution function (RDF) plot between nanotube and water molecules as shown in Fig. 6(b).

Fig. 6 (a) The interactions energy between nanotubes with water molecules (b) RDF between nanotubes and water molecules.

3.3. Ion separation

The results of the study indicated that the transport properties of CNTs and BNNTs can be used for removing water contaminants. In this research area, some experimental and simulation studies have been conducted.^17,58,59 Thus in the present study, the heavy metal separation from water via (7,7) CNT and (7,7) BNNT was studied. The results of this study revealed that ion separation was accomplished successfully in the system. Fig. 7 depicts the current–voltage profile, where the current increases as the voltage increases.

Fig. 7 Current–voltage curves for ions in the (7,7) CNT and the (7,7) BNNT. Each data point represents the average of five sets of simulations. Lines were obtained from linear regression.

This trend indicates that the number of heavy metals and water molecules passing through the (7,7) CNT and (7,7) BNNT increases as the applied voltage increased (see Fig. 8). All three ions are included. The number of ions passing through the (7,7) BNNT is greater than the ones passing through (7,7) CNT. This behaviour is related to the difference in their PMFs. In other words, the depth of the potential well for the (7,7) BNNT is deeper than that for the (7,7) CNT.

Fig. 8 (a) The number of ions passing through the nanotubes. (b) The number of water molecules passing through the nanotubes.

Incidentally, when no electric field was applied to the system, the ions were able to enter the nanotubes but they were not able to exit them. However, when the electric field was applied, the ions overcame the potential barrier and could get out of the nanotubes.

Fig. 9 illustrates the retention time for the cations (the time required for the cations to pass across the (7,7) CNT and (7,7) BNNT) in systems as a function of the applied voltage.

Fig. 9 Retention time for ions in the (7,7) CNT and the (7,7) BNNT at applied voltages.

As the Fig. 9 shows, the retention time decreases with increasing the voltage. Hence, it should be noted that the retention time is lower for the BNNT. This trend is consistent with the previous parameters such as PMF and current. As mentioned earlier, a deep potential well is produced for heavy metals inside the nanotubes and the depth of the potential well is greater for BNNT than that of the CNT. It can thus be argued that it is easier for the cations to pass through the (7,7) BNNT than the (7,7) CNT. Moreover, under the application of low electric fields for both nanotubes, there is an overlap between the retention times of cations inside the nanotubes. Nevertheless, there is no overlap when a high electric field is applied. In other words, it can be observed that in low electric field one cation enters the nanotube and would not exit until a second cation gets into the nanotube. However, cation permeates into the nanotube regardless of any support from another cation under the application of a high electric field.

3.4. Radial distribution functions of ions–water

To clarify the structure change in each type of ion in the simulation box, we calculated the RDFs of ions–water (see Fig. 10) in two type systems. Fig. 10(a) shows the RDF for Cu²⁺–water, Fig. 10(b) illustrates the RDF for Hg²⁺–water and Fig. 10(c) shows the RDF for Pb²⁺–water. It can be noted that RDF is zero for a short distance which is due to strong repulsive forces. For ions, the position of the first maximum and the magnitude of peaks are different which indicates that the hydration number of the ions is different. Fig. 10(a)–(c) shows that with an increase in the ion size (Cu²⁺ < Hg²⁺ < Pb²⁺), the magnitude of the peaks decreases and the position of peaks RDF increases. These results confirm the findings of other papers in the related researches.^60–62

Fig. 10 Ions–water radial distribution functions in the simulation box of CNT(7,7) and BNNT(7,7): (a) RDF Cu²⁺–water, (b) RDF Hg²⁺–nanotubes, (c) RDF Pb²⁺–nanotubes.

4. Conclusions

In this paper, MD simulation was used to investigate and analyse the transport and selectivity properties of the (7,7) CNT and (7,7) BNNT. The results indicate that heavy metals with different ratios cross these nanotubes. In contrast, none of the anions were even able to enter the nanotubes. The simulation results showed that the separation of ions across the selected nanotubes was related to the applied voltage. It can be concluded that by applying an electric field, it has an impact on properties of the systems such as PMF, flow rate of water, the ionic current and retention time of ions. Finally, it can be maintained that the results of the study highlight the significant capability of the CNT and BNNT in removing heavy metal from water.

Acknowledgements

We thank the University of Tabriz and Iranian Nanotechnology Initiative Council for the support provided.

Notes and references

1. H. Furukawa, N. Ko, Y. B. Go, N. Aratani, S. B. Choi, E. Choi, A. Ö. Yazaydin, R. Q. Snurr, M. O'Keeffe, J. Kim and O. M. Yaghi, Science, 2010, 329, 424–428.
2. W. Zhou, X. Bai, E. Wang and S. Xie, Adv. Mater., 2009, 21, 4565–4583.
3. N. L. Rosi, J. Eckert, M. Eddaoudi, D. T. Vodak, J. Kim, M. O'Keeffe and O. M. Yaghi, Science, 2003, 300, 1127–1129.
4. J. Gao, S.-P. Sun, W.-P. Zhu and T.-S. Chung, J. Membr. Sci., 2014, 452, 300–310.
5. R. Wang, S. Guan, A. Sato, X. Wang, Z. Wang, R. Yang, B. S. Hsiao and B. Chu, J. Membr. Sci., 2013, 446, 376–382.
6. H. Yoo and S.-Y. Kwak, J. Membr. Sci., 2013, 448, 125–134.
7. K. Huang, Y. Xiu and H. Zhu, Desalin. Water Treat., 2013, 51, 1–9.
8. B. Alyüz and S. Veli, J. Hazard. Mater., 2009, 167, 482–488.
9. A. G. El Samrani, B. S. Lartiges and F. Villiéras, Water Res., 2008, 42, 951–960.
10. P. Ghosh, A. N. Samanta and S. Ray, Desalination, 2011, 266, 213–217.
11. E. Cséfalvay, V. Pauer and P. Mizsey, Desalination, 2009, 240, 132–142.
12. H. Yanagisawa, Y. Matsumoto and M. Machida, Appl. Surf. Sci., 2010, 256, 1619–1623.
13. S. Iijima, Nature, 1991, 354, 56–58.
14. J.-Y. Guo, C.-X. Xu, F.-Y. Sheng, Z.-L. Jin, Z.-L. Shi, J. Dai and Z.-H. Li, Quantum Matter, 2013, 2, 181–186.
15. M. Meyyappan, Carbon nanotubes: science and applications, CRC press, 2004.
16. S. Kar, R. C. Bindal and P. K. Tewari, Nano Today, 2012, 7, 385–389.
17. B. Corry, J. Phys. Chem. B, 2008, 112, 1427–1434.
18. P. S. Goh, A. F. Ismail and B. C. Ng, Desalination, 2013, 308, 2–14.
19. J. Azamat and J. Sardroodi, Monatsh. Chem., 2014, 145, 881–890.
20. R. Das, M. E. Ali, S. B. A. Hamid, S. Ramakrishna and Z. Z. Chowdhury, Desalination, 2014, 336, 97–109.
21. D. Golberg, Y. Bando, C. C. Tang and C. Y. Zhi, Adv. Mater., 2007, 19, 2413–2432.
22. A. Rubio, J. L. Corkill and M. L. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 5081–5084.
23. N. G. Chopra, R. J. Luyken, K. Cherrey, V. H. Crespi, M. L. Cohen, S. G. Louie and A. Zettl, Science, 1995, 269, 966–967.
24. C. Y. Won and N. R. Aluru, Chem. Phys. Lett., 2009, 478, 185–190.
25. H. Ebro, Y. M. Kim and J. H. Kim, J. Membr. Sci., 2013, 438, 112–125.
26. D. Tang and D. Kim, Chem. Phys., 2014, 428, 14–18.
27. T. Nanok, N. Artrith, P. Pantu, P. A. Bopp and J. Limtrakul, J. Phys. Chem. A, 2008, 113, 2103–2108.
28. M. Thomas, B. Corry and T. A. Hilder, Small, 2014, 10, 1453–1465.
29. L. A. Richards, A. I. Schäfer, B. S. Richards and B. Corry, Small, 2012, 8, 1701–1709.
30. L. A. Richards, B. S. Richards, B. Corry and A. I. Schäfer, Environ. Sci. Technol., 2013, 47, 1968–1976.
31. M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363.
32. J. K. Holt, H. G. Park, Y. Wang, M. Stadermann, A. B. Artyukhin, C. P. Grigoropoulos, A. Noy and O. Bakajin, Science, 2006, 312, 1034–1037.
33. B. J. Hinds, N. Chopra, T. Rantell, R. Andrews, V. Gavalas and L. G. Bachas, Science, 2004, 303, 62–65.
34. A. Bala Subramaniam, M. Abkarian, L. Mahadevan and H. A. Stone, Nature, 2005, 438, 930.
35. T. A. Hilder, D. Gordon and S.-H. Chung, Small, 2009, 5, 2183–2190.
36. T. A. Hilder, R. Yang, D. Gordon, A. P. Rendell and S.-H. Chung, J. Phys. Chem. C, 2012, 116, 4465–4470.
37. J. Su and H. Guo, J. Phys. Chem. B, 2012, 116, 5925–5932.
38. G. Hummer, J. C. Rasaiah and J. P. Noworyta, Nature, 2001, 414, 188–190.
39. C. Y. Won and N. R. Aluru, J. Am. Chem. Soc., 2007, 129, 2748–2749.
40. P. Li, B. P. Roberts, D. K. Chakravorty and K. M. Merz, J. Chem. Theory Comput., 2013, 9, 2733–2748.
41. Y. Shim, Y. Jung and H. J. Kim, Phys. Chem. Chem. Phys., 2011, 13, 3969–3978.
42. C. M. Breneman and K. B. Wiberg, J. Comput. Chem., 1990, 11, 361–373.
43. L. Kalé, R. Skeel, M. Bhandarkar, R. Brunner, A. Gursoy, N. Krawetz, J. Phillips, A. Shinozaki, K. Varadarajan and K. Schulten, J. Comput. Phys., 1999, 151, 283–312.
44. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
45. J. Azamat, A. Khataee and S. Joo, J. Mol. Model., 2014, 20, 1–9.
46. J. Azamat, A. Khataee and S. W. Joo, J. Mol. Graphics Modell., 2014, 53, 112–117.
47. J. Azamat, J. J. Sardroodi and A. Rastkar, RSC Adv., 2014, 4, 63712–63718.
48. J. Azamat and J. J. Sardroodi, J. Comput. Theor. Nanosci., 2014, 11, 2611–2617.
49. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
50. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092.
51. A. D. MacKerell, D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiórkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616.
52. R. Kjellander and H. Greberg, J. Electroanal. Chem., 1998, 450, 233–251.
53. G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1977, 23, 187–199.
54. B. Roux, Comput. Phys. Commun., 1995, 91, 275–282.
55. S. Joseph and N. R. Aluru, Nano Lett., 2008, 8, 452–458.
56. C. Y. Won, S. Joseph and N. R. Aluru, J. Chem. Phys., 2006, 125, 114701.
57. C. Y. Won and N. Aluru, J. Phys. Chem. C, 2008, 112, 1812–1818.
58. A. Kalra, S. Garde and G. Hummer, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 10175–10180.
59. C. Song and B. Corry, J. Phys. Chem. B, 2009, 113, 7642–7649.
60. J. M. Di Leo and J. Marañón, J. Mol. Struct.: THEOCHEM, 2004, 709, 163–166.
61. R. W. Impey, P. A. Madden and I. R. McDonald, J. Phys. Chem., 1983, 87, 5071–5083.
62. S. H. Lee and J. C. Rasaiah, J. Phys. Chem., 1996, 100, 1420–1425.

---